弹性波传播的低数值频散波场模拟方法

张朝元

（大理学院 数学与计算机学院，云南 大理671003）

研究地震波在地球介质中的传播规律是认识地球内部结构和进行油气资源勘探等研究活动的重要内容。波动方程数值模拟方法是了解地震波传播规律的一项基本手段，为地震波的传播机理研究提供了重要依据。弹性波方程是一种常见的地震波方程，被广泛地应用于地震波研究中。准确正演模拟弹性波传播是研究地震各向异性和AVO反演的基础。因此，本文基于弹性波方程，研究地震波传播的正演数值模拟方法。

常见的正演数值模拟方法依据微分项处理的数值方式而不同，如射线追踪法［1］、有限元法［2］、伪谱法［3］、反射率法［4］和有限差分法［5－7］等。利用这些方法求解波动方程数值解时，会遇到因离散求解波动方程而产生的伪波动现象，即所谓的网格频散或数值频散，尤其是在有较大梯度的波场附近或网格点较粗时，频散现象更为严重，这样极大地降低了地震波模拟精度。为此，人们开展了大量的研究工作并从频散前校正和频散后校正提出大量压制数值频散的数值模拟方法［8－16］。频散前校正方法以高阶数值格式和新型高阶微分算子为代表。高阶数值格式［6，7］不一定意味着会降低数值频散［9］，且存在边界处理困难和不易并行等缺点。以近似解析离散化算子［17］（记为NAD）为代表的新型高阶微分算子［18－22］包含位移和梯度等信息，因此，NAD算子不仅能有效地压制数值频散且适应于大规模并行计算。频散后校正方法主要有通量校正传输技术［10］（记为FCT）。Boris和Book等人把用于流体动力学数值仿真问题的通量校正传输技术推广应用于地震波数值模拟上，取得了许多有价值的结果［8－16］。

为有效地压制数值频散以提高地震波场模拟精度，在前人的基础上，本文提出了弹性波传播的八阶FNRK方法。该方法是将八阶NAD算子［23－25］替代差分算子进行频散前校正而采用FCT技术［10］作为频散后校正的一种 Runge－Kutta方法［26］。基于双层均匀各向同性介质和三层横向各向同性介质的地震波数值实验表明，同八阶 NAD-RK方法、八阶Lax-Wendroff（LWC）方法和八阶交错网格（SG）方法相比，本文提出的八阶FNRK方法能有效地压制数值频散并最大程度地提高数值模拟记录的信噪比，能有效地应用于弹性波复杂介质模拟研究。

1 方法原理

下面，我们以二维弹性波方程来阐述本文提出的八阶FNRK方法的基本原理。设二维弹性波传播方程如下

其中：下标j＝1，3；ρ＝ρ（x，z）和σij分别代表介质密度和应力，ui和fi分别为i方向的位移分量和力源函数分量。在地震波场模拟实验中，通常选择随时间变化的震源函数为

1.1 空间网格离散

为了有效压制因空间离散化所产生的数值频散，我们引入近似解析离散算子来替代差分算子进行空间偏导数高阶离散。

其中G是二阶微分算子。

再令vi＝∂ui/∂t（i＝1，2，3），V＝（v1，v2，v3）T，则方程（3）式变为

又令W＝（U，V）T，则式（4）变为

这样，我们得到了与弹性波传播方程（1）式等价的方程组（5）式，（5）式中的微分算子L包含了关于空间的二阶和三阶偏导数。在这里，我们选择利用近似解析离散算子来对空间偏导数进行八阶离散，具体的离散公式［23－25］见附录 A。

1.2 时间离散

为求解具有常微分方程组形式的弹性波传播方程等价方程（5）式，我们采用三级三阶的Runge-Kutta方法［26］来对时间导数进行离散，简化的计算公式如下

其中Wn＝W（nΔt）。把向量W＝（U，V）T代入（6）式，就有

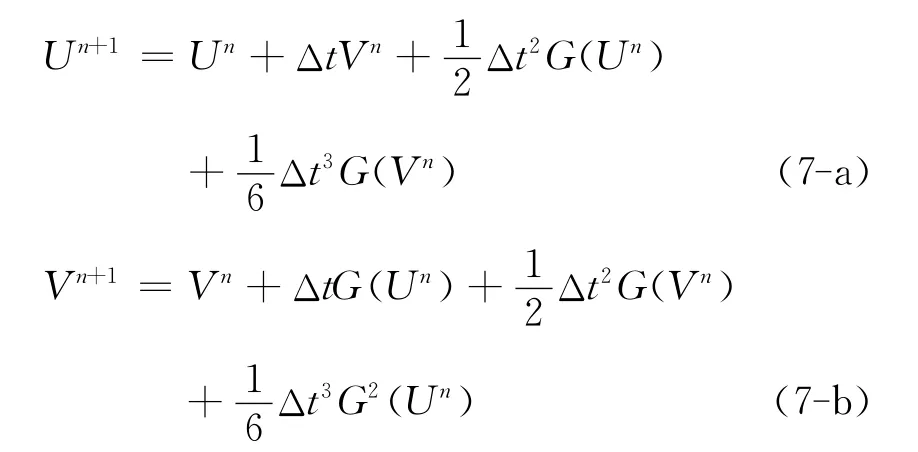
其中偏微分算子G2＝G·G。

把用于求解弹性波传播方程（1）式的离散公式（6）式或（7）式简称为八阶 NAD-RK方法。

1.3 八阶FNRK方法

由（6）式或（7）式模拟地震弹性波在介质模型中的传播，能得到数值模型中所有网格点在任意时刻各方向的位移值和粒子速度值。为在数值模拟中有效消除数值频散的影响以提高计算精度，我们引入通量校正传输技术［10］。采用FCT技术来校正八阶NAD-RK方法模拟弹性波传播后的数值频散，即得到基于弹性波传播方程的低数值频散波场模拟方法，称为八阶FNRK方法。该方法包括下面5个步骤。

（1）给定初始值（其 中

（2）利用离散公式（6）式或（7）式来计算（其中n≥0）。

（3）漫射通量计算。

①计算第n个和n＋1个时间步长的漫射通量为

其中：λ，μ（0≤λ，μ≤1）为漫散通量校正系数。

②在压制网格频散引起的伪波动同时也导致了一定的波场振幅损失，为此利用漫射通量A，B来平滑离散方程（6）式或（7）式的解

（4）反漫射通量计算过程。

①用被修改过的解和八阶 NAD-RK 方法模拟得到的解来计算反漫射通量，即

②利用反漫射通量修正平滑解，即可得到消除数值频散后的正确解

其中：

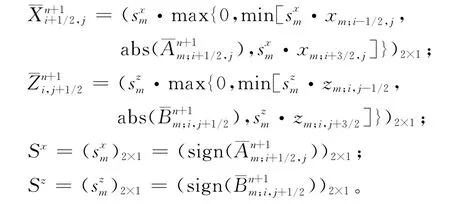
这里，m（1，2）表示向量X，Z，Sx，Sz中的第m个元素，max代表取最大值，min代表取最小值，sign代表取数学符号，abs表示取绝对值。

（5）接着回到步骤（2），重复步骤（2）至步骤（4），如此循环直到满足结束条件，即可得到所需的结果。

2 数值模拟

为验证本文提出的八阶FNRK方法在弹性波模拟中具有低数值频散，我们用八阶FNRK方法来模拟弹性波在均匀各向同性（记为HI）介质和横向各向同性（记为TI）介质中的传播。

2.1 双层HI介质

地震波在介质不连续面发生反射、折射，并携带着地质构造信息的上行波被地震台站接收而形成所谓的地震记录。基于这些地震记录，由地震波反演成像方法推断出地下结构，从而引导人们对深层内部结构进行认识。因此，准确模拟地震波在地下介质波阻抗不连续处的反射、折射具有重要意义。而双层介质模型是多层介质模型的基础，为此，我们首先考察八阶FNRK方法模拟弹性波在双层均匀各向同性介质中的传播。

设双层HI介质模型的计算区域为0≤x，z≤9km，层间界面位于深度z0≤4.5km处。上层介质中的弹性系数和密度分别为λ1＝4.8 GPa，μ1＝6.5GPa，ρ1＝3.2g/cm3；下层介质中的弹性系数和密度分别为λ2＝6.0GPa，μ2＝24.0GPa，ρ2＝1.5g/cm3。震源位于模型中心，震源函数为f0＝25Hz的Ricker子波，且f1（x）＝f3（x）＝f（t）。接收器位置为R（5km，4km）。设时间步长为Δt＝3ms，空间步长为Δx＝Δz＝30m。

图1分别为八阶FNRK方法（图1-A）、八阶NAD-RK方法（图1-B）、八阶LWC方法（图1-C）和八阶SG方法（图1-D）模拟得到t＝1.2s时刻在水平位移方向的波场瞬时快照。图2分别为由八阶FNRK 方法（图2-A）、八阶 NAD-RK 方法（图2-B）、八阶 LWC方法（图2-C）和八阶SG 方法（图2-D）模拟得到在R处从时间t＝0s到t＝1.2s在水平位移方向的波形记录。从图1和图2可看出，由八阶FNRK方法模拟得到的波场快照和波形记录无任何可见的数值频散，而同阶的NAD-RK方法、LWC方法和SG方法却有着严重的数值频散。这说明八阶FNRK方法在粗网格条件下对于弹性波在强间断层状介质中有着很好的波传播模拟效果。

2.2 三层TI介质

为检验八阶FNRK方法的模拟效果和优越性，我们选择三层TI介质模型进行波场模拟，同时与八阶NAD-RK方法、八阶LWC方法和八阶SG方法进行比较。其中，三层TI介质模型中的弹性系数和介质密度如表1所示。设模型的计算区域为0≤x，z≤12km，采用频率f0＝20Hz的Ricker子波作为震源，且f1＝f3＝f（t），震源位于计算区域中心，取空间步长为Δx＝Δz＝40m，取时间步长为Δt＝2ms。

图3给出了粗网格（Δx＝Δz＝40m）情况下在t＝1.2s时刻分别由八阶FNRK方法（图3－A）、八阶 NAD-RK 方法（图3-B）、八阶 LWC方法（图3-C）和八阶SG方法（图3-D）模拟得到在水平位移方向的波场瞬时快照。从图3可以看出，4种方法模拟得到的数值波场几乎一样，但是图3-B表明八阶NAD-RK方法有轻度的数值频散误差，而图3-C和图3-D表明八阶LWC方法和八阶SG方法均有着严重的数值频散现象。而在同样的计算条件下，本文提出的八阶FNRK方法得到了清晰的波场快照（图3-A），无可见的数值频散。可见，在粗网格条件下八阶FNRK方法在压制数值频散上明显优越于八阶LWC方法和八阶SG方法，也好于八阶NAD-RK方法。

图1 双层介质下t＝1.2s时刻水平位移方向的波场瞬时快照Fig.1 Snapshots of wave fields at time t＝1.2sand in the horizontal displacement direction under the two-layer media

图2 双层介质下在接收点R（5km，4km）处的波形记录Fig.2 Waveforms at the receiver point R（5km，4km）and in the horizontal displacement direction under the two-layer media

图3 粗网格（Δx＝Δz＝40m）条件下t＝1.2s时刻水平位移方向的波场瞬时快照Fig.3 Snapshots of wave fields at time t＝1.2sin the horizontal displacement direction under the coarse grid（Δx＝Δz＝40m）

表1 三层介质模型中的参数Table 1 Parameters used in a three-layer model

3 结论

如何有效地消除波场模拟中的数值频散是地震波正演数值模拟方法研究的重要内容之一。基于弹性传播方程，本文以近似解析离散算子替代差分算子对空间偏导数进行八阶离散，以Runge－Kutta方法对时间导数进行三阶离散，从而实现频散前的校正；而采用通量校正传输技术进行频散后校正，最终得到一种频散前校正和频散后校正有效结合的综合校正数值频散的方法，即八阶FNRK方法。为考察本文所提出的八阶FNRK方法在压制数值频散上的效果，我们将其应用于模拟弹性波在双层HI介质和三层TI介质中的传播。模拟结果表明，该方法在压制数值频散上明显优越于传统的高阶有限差分方法。同时，该方法对在大尺度复杂介质中的地震波传播有着很强的模拟适应能力。因此，本文提出的八阶FNRK方法有望广泛地用于大尺度复杂地质构造介质中的地震波场模拟和分析。

［1］Chapman C H，Shearer P M.Ray tracing in azimuthally anisotropic media-Ⅱ：Quasi shear wave coupling［J］.Geophys J，1989，96：65－83.

［2］杨顶辉.双相各向异性介质中弹性波方程的有限元解法及波场模拟［J］.地球物理学报，2002，45（4）：575－583.Yang D H.Finite element method of the elastic wave equation and wave field simulation in two-phase anisotropic media［J］.Chinese Journal of Geophysics，2002，45（4）：575－583.（In Chinese）

［3］Komatitsch D，Vilotte J P.The spectral element method：An efficient tool to simulate the seismic responses of 2Dand 3Dgeological structures［J］.Bull Seism Soc Am，1998，88：368－392.

［4］Chen X F.A systematic and efficient method of computing normal modes for multi-layered half space［J］.Geophys J Int，1993，115：391－409.

［5］Kelly K R，Wave R W，Treitel S.Synthetic seismograms：A finite-difference approach［J］.Geophysics，1976，41：2－27.

［6］Dablain M A.The application of high-order differencing to scalar wave equation［J］.Geophysics，1986，51：54－66.

［7］董良国，马在田，曹景忠，等.一阶弹性波方程交错网格高阶差分解法［J］.地球物理学报，2000，43（3）：411－419.Dong L G，Ma Z T，Cao J Z，etal.A staggered-grid high-order difference method of one-order elastic wave equation［J］.Chinese Journal of Geophysics，2000，43（3）：411－419.（In Chinese）

［8］Book D L，Boris J P，Hain K.Flux-corrected transport，II：generalization of the method［J］.J Comput Phys，1975，18（3）：248－283.

［9］Fei T，Larner K.Elimination of numerical dispersion in finite-difference modeling and migration by fluxcorrected transport［J］.Geophysics，1995，60（6）：1830－1842.

［10］杨顶辉，滕吉文.各向异性介质中三分量地震记录的FCT有限差分模拟［J］.石油地球物理勘探，1997，32（2）：181－190.Yang D H，Teng J W.FCT finite difference modeling of three-component seismic records in anisotropic medium［J］.OGP，1997，32（2）：181－190.（In Chinese）

［11］Yang D H，Liu E，Zhang Z J，etal.Finitedifference modeling in two-dimensional anisotropic media using a flux-corrected transport technique［J］.Geophys J Int，2002，148：320－328.

［12］郑海山，张中杰.横向各向同性（VTI）介质中非线性地震波场模拟［J］.地球物理学报，2005，48（3）：660－671.Zheng H S，Zhang Z J.Synthetic seismograms of nonlinear seismic waves in isotropic（VTI）media［J］.Chinese Journal of Geophysics，2005，48（3）：660－671.（In Chinese）

［13］吴国忱，王华忠.波场模拟中的数值频散分析与校正策略［J］.地球物理学进展，2005，20（1）：58－65.Wu G C，Wang H Z.Analysis of numerical dispersion in wave-field simulation［J］.Progress in Geophysics，2005，20（1）：58－65.（In Chinese）

［14］Zheng H S，Zhang Z J，Liu E.Non-linear seismic wave propagation in anisotropic media using fluxcorrected transport technique［J］.Geophys J Int，2006，165：943－956.

［15］王珺，杨长春，冯英杰.用优化通量校正传输技术压制数值模拟的频散［J］.勘探地球物理进展，2007，30（4）：252－256.Wang J，Yang C C，Feng Y J.Elimination of numerical dispersion in finite-difference modeling by optimized flux-corrected transport［J］.PEG，2007，30（4）：252－256.（In Chinese）

［16］陈可洋，杨微，刘洪林，等.二阶弹性波动方程高精度交错网格波场分离数值模拟［J］.物探与化探，2009，33（6）：700－704.Chen K Y，Yang W，Liu H L，etal.Wave field separation numerical modeling of second order elastic wave equation by high-precision staggered-grid finite difference scheme［J］.Geophysical ＆ Geochemical exploration，2009，33（6）：700－704.（In Chinese）

［17］Kondoh Y，Hosaka Y，Ishii K.Kernel optimum nearly-analytical discretization algorithm applied to parabolic and hyperbolic equations［J］.Computers Math Appl，1994，27（3）：59－90.

［18］Yang D H，Teng J W，Zhang Z J，etal.A nearlyanalytic discrete method for acoustic and elastic wave equations in anisotropic media［J］.Bull Seism Soc Am，2003，93（2）：882－890.

［19］Yang D H，Peng J M，Lu M，etal.Optimal nearlyanalytic discrete approximation to the scalar wave equation［J］.Bull Seism Soc Am，2006，96（3）：1114－1130.

［20］Yang D H，Song G J，Chen S，etal.An improved nearly analytical discrete method：an efficient tool to simulate the seismic response of 2-D porous structures［J］.J Geophys Eng，2007，4：40－52.

［21］Yang D H，Wang N，Chen S，etal.An explicit method based on the implicit Runge-Kutta algorithm for solving the wave equations［J］.Bull Seism Soc Am，2009，99（6）：3340－3354.

［22］王磊，杨顶辉，邓小英.非均匀介质中地震波应力场的WNAD方法及其数值模拟［J］.地球物理学报，2009，52（6）：1526－1535.Wang L，Yang D H，Deng X Y.A WNAD method for seismic stress-field modeling in heterogeneous media［J］.Chinese J Geophys，2009，52（6）：1526－1535.（In Chinese）

［23］Tong P，Yang D H，Hua B L，etal.A high-order stereo-modeling method for solving wave equations［J］.Bulletin of the Seismological Society of America，2013，103（2）：811－833.

［24］Zhang C Y，Li X，Ma X，etal.A Runge-Kutta method with using eighth-order nearly-analytic spatial discretization operator for solving a 2Dacoustic wave equation［J］.Journal of Seismic Exploration，2014，23（3）：279－302.

［25］Zhang C Y，Ma X，Yang L，etal.Symplectic partitioned Runge-Kutta method based on the eighthorder nearly analytic discrete operator and its wavefield simulations［J］.Applied Geophysics，2014，11（1）：89－106.

［26］Qiu J X，Li T G，Khoo B C.Simulations of compressible two-medium flow by Runge-Kutta discontinuous Galerkin methods with the ghost fluid method［J］.Commun Computs Phys，2008，3：479－504.

附录A：空间高阶偏导数的逼近公式

利用局部插值近似方法，可以得到位移和粒子速度关于空间的二阶和三阶偏导数的逼近公式，具体推导过程见参考文献［23－25］。这里，只给出了关于位移的高阶偏导数的计算公式

其中：Δx，Δz分别代表x方向和z方向的空间步长。

把（A-1）～（A-7）式中的u换成v就得到关于粒子速度的二阶和三阶偏导数的逼近公式。