波动方程正演模拟边界条件的比较分析

付小波，韩 超，原健龙，余嘉顺，2

（1.成都理工大学 地球物理学院，成都610059；2.新西兰皇家地质与核科学研究所，惠灵顿）

边界条件是地震波数值模拟方法技术中的一项重要内容。许多专家学者从不同角度提出多种构造边界条件的方法。1977年，Clayton与Engquist［1］根据旁轴近似理论（Claerbout［2］；Claerbout与Johnson［3］），提出利用一系列不同近似精度的单程波动方程来吸收模型边界的反射能量，称作Clayton-Engquist（下文采用简略记号CE来表达）边界条件。1978年，Reynolds通过对波动方程的分解得到了透明边界条件［4］（下文采用简略记号TBC来表达）。1994年，Berenger针对电磁波传播模拟，提出了一种高效的吸收边界条件［5］，即完全匹配层（Perfectly Matched Layer，PML）。Berenger结合实际理论模型证明了该方法可以很好地吸收来自各个方向、各种频率的电磁波。1995年，Frank，Hastings等将PML的算法思想引入弹性波模拟中，建立了弹性波场模拟的PML吸收边界条件［6］。

此后，人们针对这些边界条件的质量与效率做了一些比较性研究。2006年，李景叶、陈小宏等分别采用CE边界条件和PML边界条件做一阶的速度－应力弹性波方程数值模拟，得到不同的模拟图像［7］。经过观察比较，得出PML边界的效果优于CE边界的定性认识。同年，邢丽也分别用CE边界条件和PML边界条件进行二维声波方程数值模拟，以图像显示观察比较的方式，说明了PML边界条件明显好于CE边界条件［8］。

上述基于图件观察比较得出的定性结论对一般性的勘探成像模拟是具有指导意义的；但是对于弱能量波场现象的模拟来说，就显得不够精细了。比如在模拟粗糙界面的弱散射现象时，其散射能量与边界条件残存反射能量在强度上可能是同级的，如果边界条件选择不当，边界反射造成的干扰甚至会将目标弱散射完全淹没。在此情况下，必须对边界条件的吸收效果有定量的精确把握，才能保证目标现象模拟的可行性。因此，对上述几种边界条件的吸收效果作高精度比较分析，得出精确的定量结论，就显得至关重要。本文对TBC边界条件、CE边界条件和PML边界条件的吸收效果进行了精细的定量模拟比较研究。

1 声波模拟方程与边界条件

为了对3种吸收边界条件的数值计算效果做比较，我们考虑一个均匀的二维声场介质空间Ω＝｛（x，z）｜0≤x≤X，0≤z≤Z｝以及时间区间τ＝｛t｜0≤t≤T｝，在此空间上声波的传播速度为v。在此空间上的声波传播过程由如下声波方程［9］决定

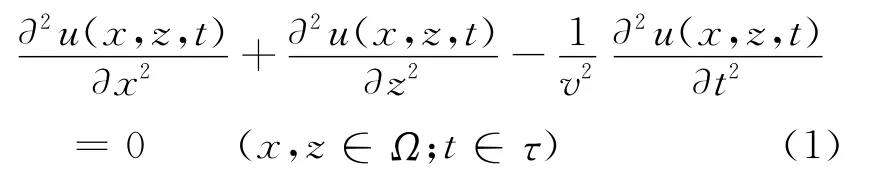
我们用δ＞0对Ω做空间等距分割，用Δ＞0对τ做时间等距分割，并对（1）式中的时间二阶导数和空间二阶导数分别采用二阶中心差分和四阶中心差分来离散。整理后得到如下关于波场传播的离散递推关系

上式中表示k时刻声波场在坐标位置为（i，j）的那个质点上的振幅。其中G为空间导数的四阶差分

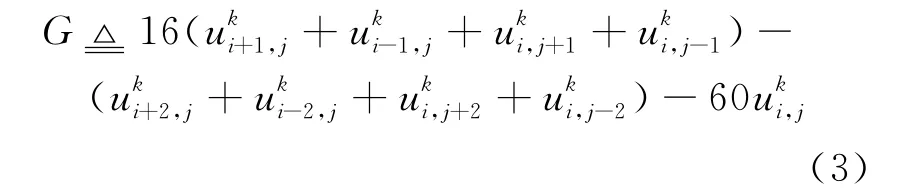
1.1 透明边界条件

Reynolds根据标量声波方程（1）得到的透明边界条件为

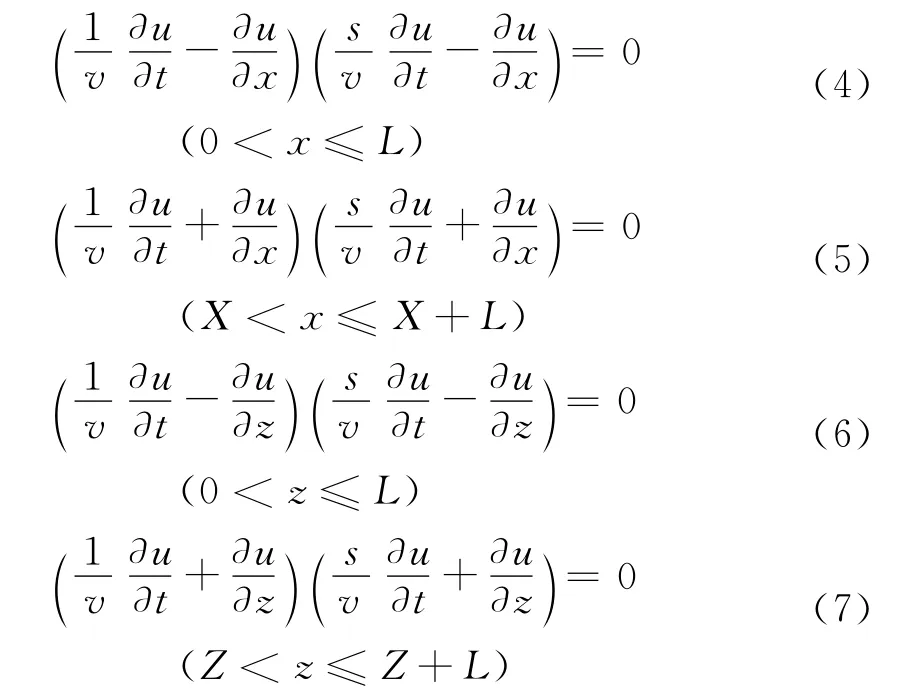
1.2 Clayton-Engquist边界条件

Clayton和Engquist提出的一系列不同精度的吸收边界条件中，如下二阶近似边界条件［1］应用得最为普遍

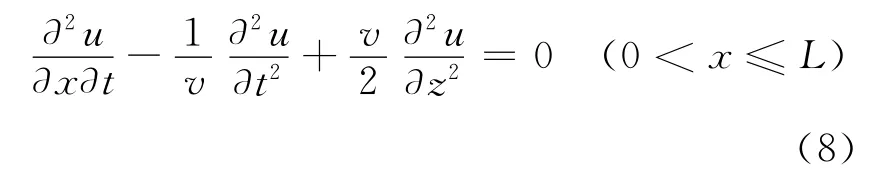
1.3 PML边界条件

二维声波方程的PML控制方程［10］为

其中ux，uz，u′x，u′z是中间变量；d（x），d（z）分别是x方向和z方向的衰减系数，其函数表达式［11］为

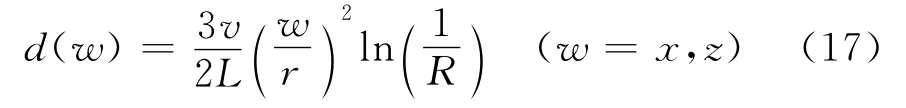
式中：R为反射系数；L为边界层厚度；w为计算网格点到内边界的距离。

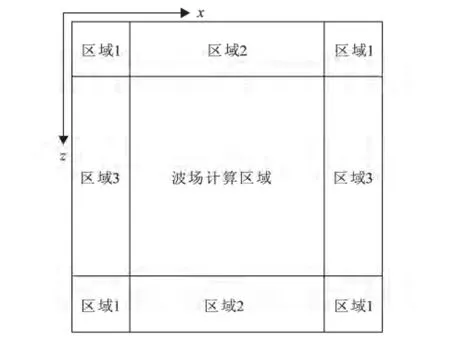
图1 PML边界区域分布示意图Fig.1 Schematic diagram for PML boundary

因为在二维声场中任意方向传播的波都可以分解为沿x方向和沿z方向传播的两个波，所以，在匹配层中分别对这两个波进行衰减吸收，便可以达到对任意方向传播的波进行衰减的目的。PML边界条件的策略就是在需要的边界区域加入相应的PML层，达到衰减模型人工边界反射的目的。如图1所示，中间部分为模型区域，而四周则是用来吸收模型边界反射而镶加上去的PML层。其中各个边界区域具有如下性质：在区域1中，d（x）≠0，d（z）≠0；在区域2中，d（x）＝0，d（z）≠0；在区域3中，d（x）≠0，d（z）＝0。

2 模拟计算与结果

我们考察一个点声源所产生的波的边界反射情况，模拟计算在一个600m×600m的区域内进行。模型介质的波传播速度为1.5km/s，为理想水介质的声波速度。点声源位于模型的中央。我们用1m的间隔对模型进行离散化，采用0.000 1s的时间间隔进行模拟计算。声源信号子波函数为

其中：震源位置坐标xs＝300m，zs＝300m；信号子波主频f＝100Hz；信号延迟因子t0＝9/（4f）；信号衰减因子

图2为分别采用TBC边界条件、CE边界条件和PML边界条件进行模拟得到的在0.25s时刻的波场快照，从中能够看到3种吸收边界条件对模型边界反射都有明显的吸收效果。通过对图件的观察可以得到初步定性认识：CE边界条件与PML边界条件的吸收效果明显好于TBC边界条件。

尽管从图2中采用PML边界进行模拟得到的波场快照图几乎看不见任何边界反射的痕迹，但这并不表明边界反射不存在。事实上，如果对波场快照的能量进行适当增益之后再绘图，PML边界条件的反射波就显示出来了（图3）。

那么，PML边界反射波的能量与其他2种边界条件的反射波的能量的定量差别有多大呢？我们将通过下面的比较模拟例子来寻找此问题的答案。

3 边界条件吸收效果的模拟比较

为了更好地了解不同边界条件的吸收效果差异，我们对模型边界的垂直反射的吸收效果，不同频率成分的吸收效果、以及不同反射角的吸收效果进行比较分析。

图2 3种不同边界条件情况下在0.25s时刻的波场快照Fig.2 Snapshots of the wave field at 0.25sunder three boundary conditions

图3 PML边界条件波场快照提高增益后的显示结果Fig.3 Snapshot of the wave field with gaining process using PML under boundary conditions

3.1 垂直反射的吸收效果

为了获得3种边界条件的吸收效果，本文采用同一个模型，分别镶上不同的吸收边界条件后进行模拟。所采用的模型大小：1.2km×1.2 km，模型介质波速：1.5km/s。为了取得一个比较稳定的结果，我们在每种边界条件下均进行了5次模拟试验，各次试验的震源与接收点位置重叠，分别位于图4中的A、B、C、D与E点的位置上。其位置坐标分别为（10，600）、（20，600）、（40，600）、（80，600）、（160，600）。所用的信号源子波函数由（18）式给定，子波主频为100Hz。模拟过程是在空间离散间隔为δ＝1m的离散网格上用前述的有限差分方法进行的，模拟的时间采样间隔Δ＝0.000 1s，模拟时长为0.3s。

我们的目的是对模型左边界的反射波能量进行分析。考虑到试验记录中不但含有边界反射波，而且还含有直达波，为此需要将直达波从记录上消除，用纯净的反射波来进行比较分析，可以通过对模拟记录与仅包含直达波的记录相减来完成。

图4 垂直反射模拟实验观测系统示意图Fig.4 Simulation observation system of vertical reflection

为了得到一个仅包含直达波的记录，将模型扩大为10km×10km来进行一次模拟计算。在此情况下，由于模型边界距离源点和接收点非常遥远，模型边界反射尚未来得及传回到接收点的位置上，模拟过程（0.3s）就已经结束了。因此，这一模拟过程得到的记录只含有直达波，没有反射波。

图5和图6具体地展示了上述方法。图5的Ⅰ、Ⅱ、Ⅲ、Ⅳ分别为在扩展模型镶透明边界、CE边界以及PML边界情况下在D点激发和接收的记录。图6的3条时间记录曲线（Ⅱ’、Ⅲ’、Ⅳ’）分别为图5中Ⅱ、Ⅲ、Ⅳ减去Ⅰ的结果，为所需要的用于分析边界条件吸收效果的纯净反射波。

读取纯净反射波的波峰值，列于表1之中，可对3种边界条件的吸收差异作对比分析。从表1的数据可以看出，采用不同的边界条件，模型边界反射的强弱存在显著的差异。其中CE边界条件下的反射波峰值（表中第3列）小于TBC边界条件（表中第2列），而PML边界条件下的反射波峰值（第4列）又小于CE边界条件下的反射波峰值。这种情况在图7中体现也非常明显。而且这种相对差异在A、B、C、D与E震源/接收情况体现得非常一致。这在图8的关于CE/TBC和PML/TBC的反射波峰值比值的图示中体现得非常直观。

图5 经过直达波峰值归一化处理的全程波形记录Fig.5 Full waveform records normalised with the peak amplitude of the direct wave

图6 经过直达波峰值归一化处理的反射波波形记录Fig.6 Reflection waveform records normalised with the peak amplitude of the direct wave

表1 各记录点反射波振幅的最大峰值Table 1 Peak values of the reflected wave amplitudes recorded at each point

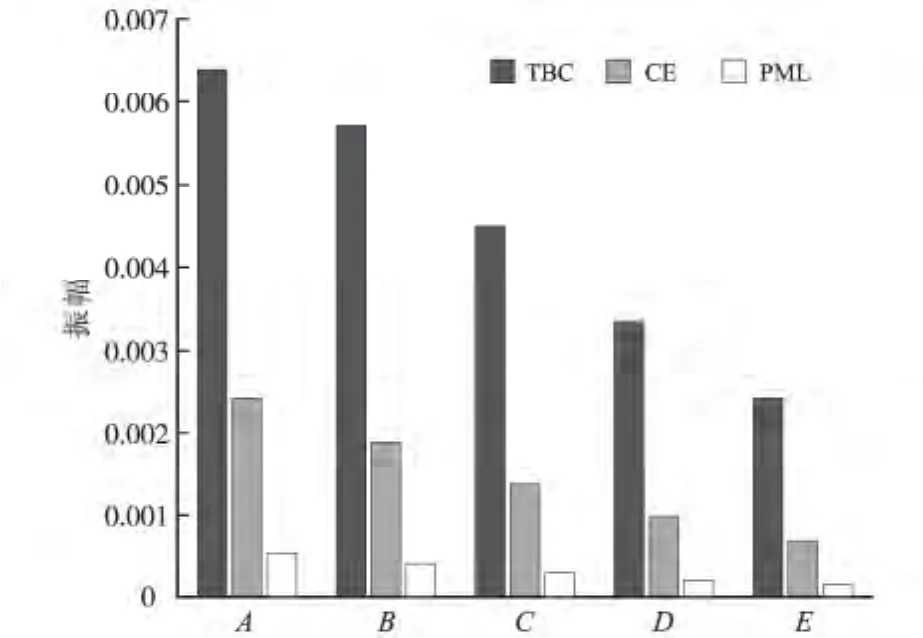
图7 3种边界条件反射波峰值的比较Fig.7 Comparison of the reflection peak values under three boundary conditions

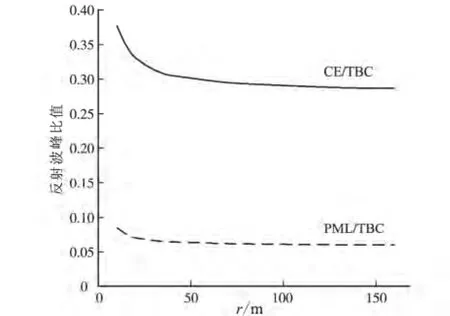
图8 振幅峰值比CE/TBC及PML/TBC随观测点与模型边界间距离的变化Fig.8 Variation of the peak ratios of CE/TBC and PML/TBC with the distance between the observation point and model boundary

当源点/接收点位置不同，上述峰值的比值存在差异。几何扩散会对反射波峰随着位置产生变化；但是，CE/TBC与PML/TBC比值已经消除了几何扩散的影响，因此CE/TBC与PML/TBC随着位置的变化必然另有原因。我们认为，这种相对位置造成的比值差异，可能是由于不同边界条件的频率响应差异引起的。当一个边界条件的响应频段较低的时候，由于对应的主频较长，就可对距离模型边界较远的模型内部波场产生影响。反之，如果一个边界条件的响应频段较高，其对距离模型边界较远的模型内部波场产生的影响就较弱。因此，CE/TBC与PML/TBC的值随着位置的变化而变化，反映了3种边界条件频率响应的差异。

通过比较试验得到如下认识：（1）在垂直于模型边界反射的情况下，CE边界条件的吸收效果优于TBC的吸收效果。在距离边界条件较远的区域，两者的相对比值有逐渐进入稳定状态的趋势（图8），据此，其稳定状态比值应该不大于0.287 5（表1）。也就是说，在进入稳定状态之后，CE边界条件的吸收效果至少比TBC边界条件好3.5（＝1/0.287 5）倍。（2）PML边界条件的吸收效果又进一步显著地优于CE边界条件的吸收效果；并且在两者逐渐进入相对稳定的状态下（图8），PML边界条件的吸收效果至少比TBC边界条件好16.5（＝1/0.060 4）倍。

3.2 不同频率成分的吸收效果

前面关于PML和CE边界条件优于TBC边界条件的结论是在源信号主频为100Hz的情况下得到的。这一结论在其他频段是否依然成立是一个需要研究的问题。为此，对于3种边界条件对不同频率波场成分的吸收效果，采用不同频率的源信号进行了一系列的模拟分析。

进行频率试验的模型与前述试验的模型相同。在选取观测点时，考虑到峰值比在D点的位置上已经相对比较稳定，所以选择D点为源点/观测点进行频率模拟实验。在5～150Hz的频段范围内，以5Hz的间隔，做了31次频率实验。用与3.1节的实验数据类似的处理方法，计算出各个频率在D点的反射波峰值的CE/TBC与PML/TBC比值，绘成曲线（图9）。从中可以看到CE/TBC在低频时变化较大。但是当频率＞50Hz时，CE/TBC相对较稳定，均在0.3左右；也就是说，在频率＞50Hz的情况下，CE边界条件的吸收效果是TBC的3倍左右；而PML/TBC呈线性上升关系，表明PML相对于TBC的吸收优势随着频率上升是逐渐变弱的。但是，在我们实验的150Hz有效范围之内，PML的吸收优势依然十分显著，即便是在150Hz的相对高频上，其吸收效果依然比TBC好10倍（PML/TBC＜0.1）以上。

图9 反射波峰值振幅比CE/TBC与PML/TBC随频率的变化曲线Fig.9 Peak reflected amplitude ratios CE/TBC and PML/TBC versus frequency change

3.3 不同反射角的吸收效果比较

上述结论是在模型边界条件的垂直反射情况下得到的。为了了解不同反射角度情况下各边界条件的吸收效果，做了一项模拟实验。由于需要覆盖较宽的反射角度，对前面用过的模型进行了扩展，此模拟实验采用的模型大小为2km×2 km，模型介质波速和模型离散间距不变。

此项模拟的观测系统如图10所示。源信号子波频率为100Hz，源点位置为S（80m，1 000 m），与模型边界的距离与原先的D点相同。在与模型左边界平行，由S点向上布置了一个700 m长、间隔为1m的观测接收排列。S点观测的反射角度为0°，而排列末端最后一个观测点接收到的反射波的反射角为

所以这个观测系统排列覆盖了［0°，77°］的反射角度范围。用与3.1节的实验数据类似的处理方法，计算出各个反射角情况下反射波峰值的CE/TBC与PML/TBC比值曲线（图11）。

图10 反射角模拟实验观测系统示意图Fig.10 Schematic diagram showing the simulation experiment observation system at the different reflection angles

图11 反射波峰值振幅比CE/TBC与PML/TBC随反射角的变化曲线Fig.11 Peak reflection amplitude ratios CE/TBC and PML/TBC versus reflection angles

在实验的75°反射角范围之内，PML相对于TBC的吸收效果优势比较稳定，受反射角的影响不大。而CE边界条件相对于TBC的吸收效果优势则随着反射角的变化存在较大的差异。在30°以内的小反射角范围内，其吸收优势稳定地保持在3.5倍左右。随着反射角变大到50多度，其吸收优势显著增强，在54°左右的时候，其吸收效果是TBC的27（＝1/0.036 7）倍左右。但是随着反射角增大，其吸收效果优势开始显著地变弱。在75°反射情况下，CE的吸收效果相对于TBC的优势已经很小了，此时的CE/TBC比值为0.67左右。也就是说，在75°反射情况下，CE的吸收效果是TBC的1.5倍左右，优势已经大幅减低。

4 分析与结论

本文针对透明边界条件、Clayton-Engquist边界以及PML边界条件的吸收效果差异进行了模拟比较分析，得出如下定量结论。

a.以对模型边界垂直反射的吸收效果来衡量，CE边界条件对100Hz的波场成分的吸收效果是TBC吸收效果的3.5倍；而PML吸收效果则是TBC吸收效果的16.5倍。在3种边界条件中，PML显著地优于其他两种边界条件。

b.CE边界条件相对于TBC边界条件的吸收优势在低频时不明显，而且变化较大；但是在频率达到50Hz后CE的吸收效果是TBC的3.5倍左右。而PML相对于TBC的吸收优势随着频率上升是逐渐变弱的；但是，在实验的150Hz有效范围之内，PML的吸收优势依然十分显著，即便是在150Hz的相对高频上，其吸收效果依然比TBC好10倍以上。

c.在实验的75°反射角范围之内，PML相对于TBC的吸收效果优势比较稳定，受反射角变化的影响不大。而CE边界条件相对于TBC的吸收效果在30°以内的小反射角范围内，其吸收优势稳定地保持在3.5倍左右。随着反射角变大到50多度，其吸收优势显著增强，在54°左右的时候，其吸收效果是TBC的27倍左右。但是随着反射角继续增大，其吸收效果优势开始显著地变弱。在75°反射情况下，CE的吸收效果相对于TBC的优势已经很小了，此时的CE/TBC为0.67左右。也就是说，在75°反射情况下，CE的吸收效果是TBC的1.5倍左右，优势已经大幅减低。如果二者的比值随角度的变化发展趋势继续保持下去，CE对TBC的优势在＞75°的大角度情况下出现逆转是完全可能的。

总的来说，在3种边界条件中，PML显著地优于其他2种边界条件。相对于其他2种边界条件，PML的吸收效果在150Hz频率范围内和75°反射角范围内始终保持稳定的相对优势。

［1］Robert Clayton，Bjorn Engquist.Absorbing boundary conditions for acoustic and elastic wave equation［J］.Bulletin of the Seismological Society of America，1977，66（11）：1529－1540.

［2］Claerbout J F.Coarse grid calculations of waves in inhomogeneous media with application to delineation of complicated seismic structure［J］.Geophysics，1970，35：407－418.

［3］Claerbout J F，Johnson A G.Extrapolation of time dependent wave forms along their path of propagation［J］.Geophysics Journal，1971，26：285－295.

［4］Reynolds A C.Boundary conditions for the numerical solution of wave propagation problems［J］.Geophysics，1978，43（6）：1099－1110.

［5］Jean-Pierre Berenger.A perfectly matched layer for the absorption of electromagnetic waves［J］.Journal of Computational Physics，1994，114：185－200.

［6］Hastings F D，Schneider J B，Broschat S L.Application of the perfectly matched layer（PML）absorbing boundary condition to elastic wave propagation［J］.Journal Acoustical Society of America，1996，100（5）：3061－3068.

［7］李景叶，陈小宏.TI介质地震波场数值模拟边界条件处理［J］.西安石油大学学报：自然科学版，2006，21（4）：20－23.Li J Y，Chen X H.Treatment of the boundary conditions in the numerical simulation of the seismic wave field in transversely isotropic（TI）medium［J］.Journal of Xi’an Shiyou University（Natural Science Edition），2006，21（4）：20－23.（In Chinese）

［8］邢丽.地震波数值模拟中的吸收边界条件［J］.上海第二工业大学学报，2006，23（4）：272－278.Xing L.Absorbing boundary conditions for the numerical simulation of acoustic waves［J］.Journal of Shanghai Second Polytechnic University，2006，23（4）：272－278.（In Chinese）

［9］田力，余嘉顺，唐红.封闭空间声场的计算机仿真初步研究［J］.计算机科学，2003，9（31）：222－223.Tian L，Yu J S，Tang H.Preliminary study on computer simulation sound wave-field in an enclosed space［J］.Computer Science，2003，9（31）：222－223.（In Chinese）

［10］王守东.声波方程完全匹配层吸收边界条件［J］.石油地球物理勘探，2003，18（1）：31－34.Wang S D.Absorbing boundary condition for acoustic wave equation by perfectly matched layer［J］.Oil Geophysical Prospecting，2003，38（1）：31－34.（In Chinese）

［11］Francis Collino，Chrysoula Tsogka.Application of the PML absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media［J］.Geophysics，2001，66（1）：294－307.