基于组合函数响应面的桥梁有限元模型修正
2015-01-04张松涵高芳清张伟伟
张松涵,高芳清,张伟伟
(1.西南交通大学土木工程学院,四川成都610031;2.西南交通大学 力学与工程学院,四川成都610031)
0 引言
近年来,基于响应面的有限元模型修正方法在工程中已得到广泛应用,其方法在于使用显式函数关系逼近设计参数与响应值之间的隐式复杂关系,与传统有限元模型修正相比,有效避免了迭代过程中重复调用有限元计算的缺点,使迭代速度大大加快[1]。
响应面模型能否准确地反映出有限元模型中的设计参数-响应值关系,是模型修正成败的关键。目前,桥梁有限元模型修正中大多采用2阶多项式或3阶多项式作为响应面函数[2],而随着函数阶次的提高和设计参数的增多,自变量数目急剧增加,在显著性检验、响应面拟合及优化求解中都会造成计算量过大,故高阶多项式函数响应面在有限元模型修正中难以普及。寻求综合能力更好、更易于通用的响应面函数是当今有待解决的重要问题。
周林仁等[3]采用高斯径向基函数响应面完成了大跨度斜拉桥有限元模型修正,证实了其拟合精度和抗噪能力满足工程应用需要;孔宪仁等[4]和秦玉灵等[5]采用1阶式-高斯组合径向基函数响应面完成蜂窝板和机翼有限元模型修正,证实其拟合能力较1阶多项式函数和高斯径向基函数有所提高;张松涵等[6]将1阶式-高斯组合径向基函数、2阶多项式、2阶式-高斯组合径向基函数、3阶多项式用于简支梁数值模型修正,经对比发现,在含有5%噪声的条件下,2阶式-高斯组合径向基函数能保持较强的拟合能力和较高的求解精度。
为验证2阶式-高斯组合径向基函数响应面在实际工程中应用的有效性,笔者通过模型修改获得合理的设计参数,在重复试验的基础上建立了模态频率响应面函数,构造残差型目标函数,利用粒子群优化算法求解,得到设计参数最优解。在保证求解精度不受影响的前提下,避免了求解过程中反复调用有限元分析与灵敏度矩阵计算,适用于结构形式复杂的桥梁有限元模型修正。
1 基于响应面的有限元模型修正方法
基于响应面的有限元模型修正通过重复试验,将复杂结构的有限元模型转化为简单的响应面数学模型[7],结合实测数据,采用优化算法寻求到响应面模型中的最优解,再代入有限元模型进行验证,从而达到模型修正的目的,其具体流程见图1。
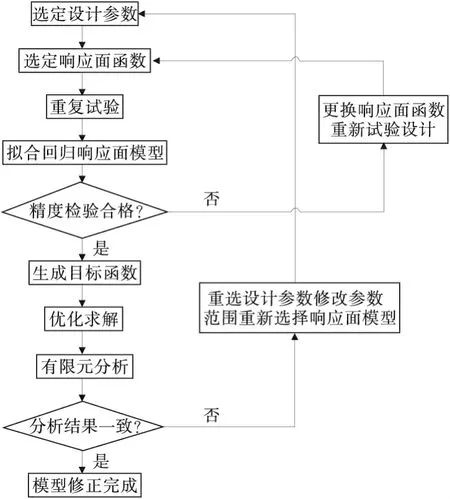
图1 基于响应面的有限元模型修正流程Fig.1 The updating process of finite element model based on response surfaces
1.1 试验设计
常见的试验设计方法有均匀试验设计、正交设计、中心复合设计、D-最优试验设计等。试验样本数量应保证样本矩阵具有一定超定次数,避免求解过程产生奇异。考虑试验因素、水平数量,笔者采用U30(303)均匀试验设计表[8],共生成30个试验样本。
1.2 组合函数响应面
径向基函数是一种径向对称的函数,形式简单、不依赖于空间维数,且具有良好的非线性拟合能力。构造RBF的线形组合模型形式如式(1):
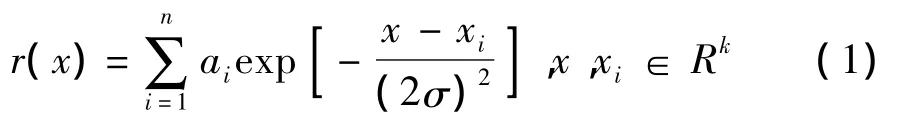
式中:[a1,a2,a3,…,an]为回归系数向量;n为修正参数的个数;x为修正参数值;xi为第i个参数的样本均值;x-x( )i表示修正参数取值到对应样本均值的Euclidean范数;σ为高斯核宽度参数。
将工程中普遍常用的2阶多项式与高斯径向基函数结合,得到改进后的响应面函数如式(2):
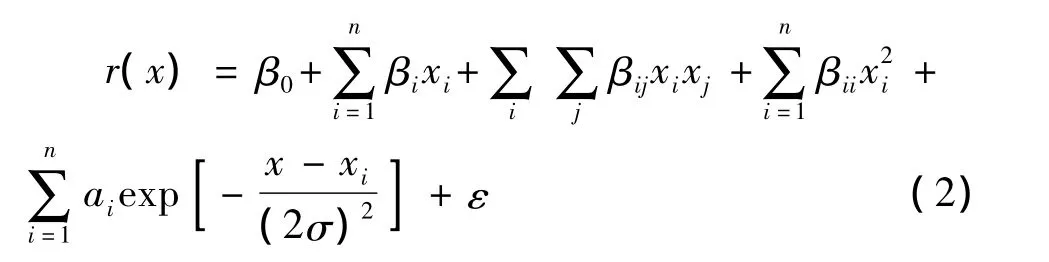
式中:核宽度参数σ一般取设计空间半径[4]。
1.3 经典最小二乘法回归响应面
将样本参数取值视为输入,计算样本频率视为输出,建立关于待定系数向量的方程:

式中:H为输入矩阵;Z为输出向量;θ为待定系数向量;e为残差向量。
要使残差平方和
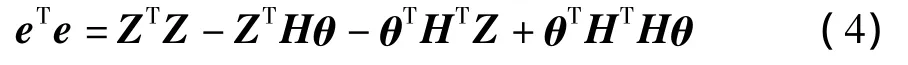
最小,对θ求偏导,令其等于0,即:
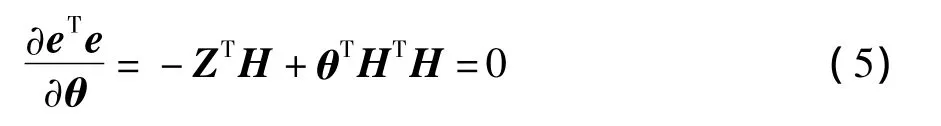
得到:

即为待定系数向量的经典最小二乘解,将其带回原组合函数,即可得到拟合后的回归响应面方程。
1.4 基于自然选择的混合粒子群优化算法
基于自然选择的混合粒子群算法将基本粒子群算法与自然选择机理相结合,其主要手段在于将整个群体在迭代过程中按照适应值排序,用群体中最优的一半粒子替换最差的一半,同时将每个粒子所经历过的历史最优点全部保留,能进行全局搜索,有效避免陷入局部极小值,且能够避开反复的灵敏度矩阵计算[9-10]。文中的目标函数优化求解均采用此算法。算法步骤如下:
1)将各个微粒按照随机原则赋予初始位置和初始速度;
2)计算各粒子的适应值并对其进行评价,把每个微粒所对应位置和适应度储存到个体极值pbest中,在所有pbest中挑出适应值最优微粒的位置xi和适应值pbest,储存到总体极值gbest中;
3)更新每个粒子的速度和位置;
4)将各个微粒的适应值与其途径过的最佳位置作比较,如果当前位置更好,则将其替换到当前最佳位置;
5)比较所有微粒的pbest和全局gbest值,更新gbest;
6)按照适应值高低将整个粒子群排序,将群体中最差的一半微粒以最好的一半替换,并保持pbest和gbest不改变;
7)达到迭代停止条件,则终止搜索,输出结果,否则返回3)更新继续搜索。
2 悬臂梁模型实验
采用Q235工字钢,将其一端固接形成悬臂梁,在距离固定螺栓中心点200 mm处有一损伤。已知弹性模量 E=2.1 ×105MPa,I=0.137 ×10-5m4,泊松比μ =0.3,密度 ρ=7 800 kg/m3,几何尺寸如图2。

图2 悬臂梁模型Fig.2 Model of cantilever beam
2.1 动力特性测试
在悬臂端设置加速度传感器,采用锤击法测试该悬臂梁的横向、竖向前两阶固有频率,见图3。

图3 悬臂梁振动实验Fig.3 Vibration test of cantilever beam
实验测得加速度时间历程曲线如图4。

图4 加速度-时间曲线Fig.4 Acceleration-time curves
经FFT变换可识别出结构的竖向前两阶固有频率。建立理想悬臂梁有限元模型,计算竖向前两阶固有频率,并与实测结果相对比:1阶固有频率的实测值 =166.26 Hz,计算值 =191.36 Hz;2 阶固有频率的实测值 =966.50 Hz,计算值 =993.80 Hz。
2.2 有限元模型改进
结合悬臂梁实际状况,发现有以下3个非理想因素:
1)竖向激振时,约束端随梁段共同运动,可认为固定端的竖向转动约束非理想,可用扭转弹簧约束代替;
2)距离螺栓中心点20 cm处存在损伤,采用单元抗弯刚度降低予以考虑;
3)模型计算长度为螺栓中心点到自由端距离,而实际悬臂梁有效长度偏短,具体数值难以准确测定。
考虑以上因素改进计算模型如图5。

图5 计算模型Fig.5 Calculation model
根据计算模型,使用ANSYS建立改进后的有限元模型如图6。

图6 有限元模型Fig.6 Finite element model
选取扭转弹簧刚度、损伤单元弹性模量、计算长度为设计参数,在可能的取值范围内进行多次试算,得到其变化对各阶频率的影响规律如图7。
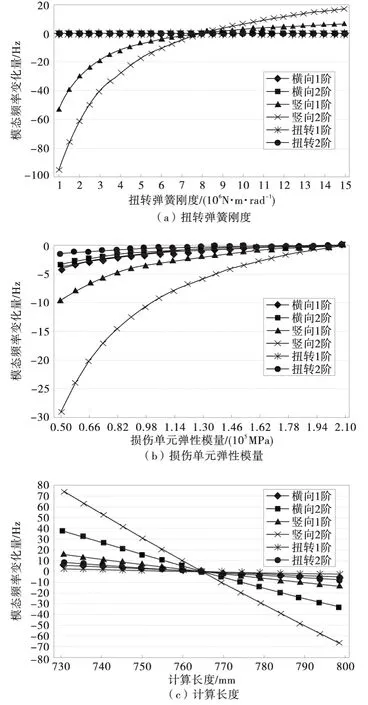
图7 设计参数对频率的影响Fig.7 Influence of the design parameters on frequency
2.3 模型修正
选用2阶式-高斯组合径向基函数为响应面函数,根据2.2章节试算所得各因素对频率的影响程度,选定设计参数的合理取值范围如表1。
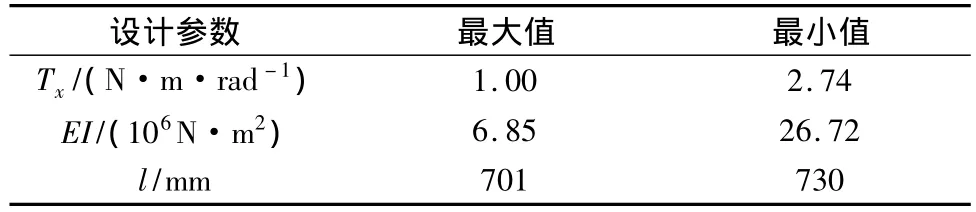
表1 设计参数修改范围Table 1 Value range of the design parameters
选用U30(303)均匀设计表形成3因素30水平均匀试验,共计30个试验样本[8]。并利用逐步消去法筛除显著性低的自变量,拟合得到横向、竖向前两阶固有频率回归响应面,各阶响应面待定系数回归值如表2。

表2 待定系数最小二乘解Table 2 Least square solution of parameters
各阶响应面有效性检验结果如表3。
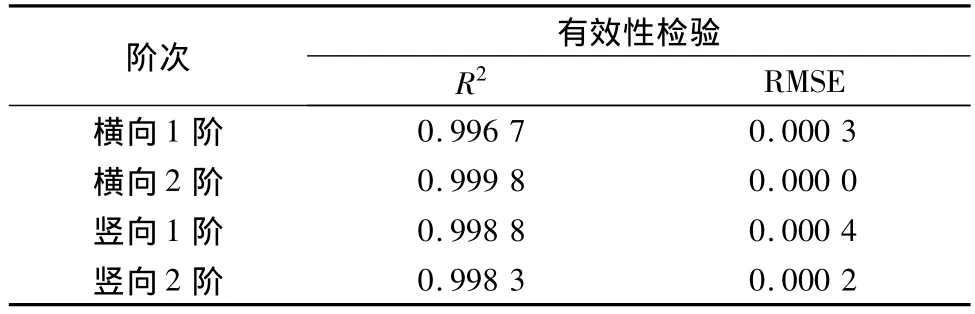
表3 响应面有效性检验Table 3 Validity tests of the response surfaces
结合各阶响应面与实测结果构造残差型目标函数如式(7):
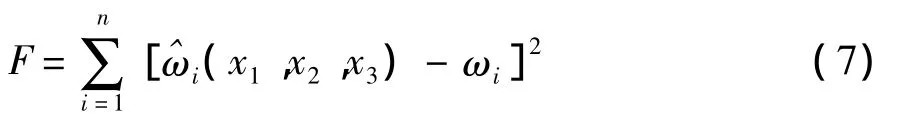
采用基于自然选择的混合粒子群算法对目标函数进行求解,迭代过程如图8。
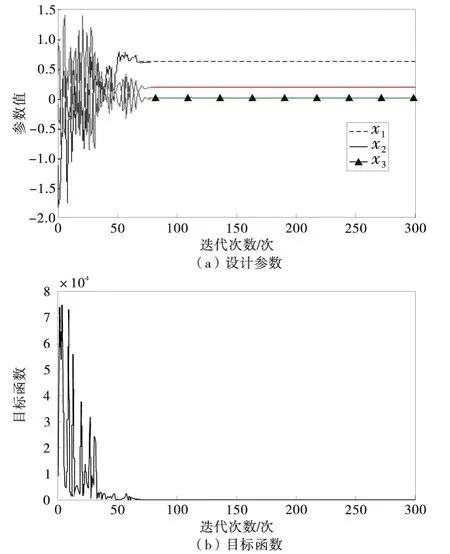
图8 优化求解迭代曲线Fig.8 Iteration curves of the optimization
将所选设计参数解除归一化,得到优化求解后的参数取值如表4。

表4 优化求解结果Table 4 Optimization results
优化后的参数值均在合理范围内,将其代回有限元模型,再次计算结构模态频率,与实测结果比较,相对误差见表5。
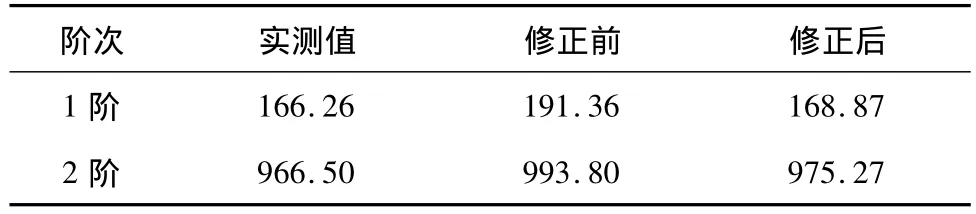
表5 修正后的竖向模态频率Table 5 Vertical modal frequencies of updated model /Hz
修正后的有限元模型竖向模态频率计算值与实测结果更加接近,能够更准确地反映实际结构的真实状态,表明该模型修正方法在实际应用中具有较好可行性。
3 贝雷梁钢桥有限元模型修正
3.1 工程概况
四川省某水电站建设工程临时用桥梁主要用于现场公路临时改线后造成的临时公路运输。该钢便桥设计使用年限<8年,设计荷载为汽-20。全桥为平桥设计,单车道,全桥长 45.3 m,宽 3.6 m,右岸有26 m长的引堤。钢桥上部结构采用型钢结构,由纵横向分配梁I 14、I 25a和10 mm厚钢板组成。I 14间距35 cm,I 25 a间距1.5 m。主纵梁选用“321”型贝雷梁、45 m主跨、采用三排双层加强贝雷梁组合型式构成,两端简支。桥梁总体布置如图9。

图9 总体布置Fig.9 General arrangement drawing
3.2 环境振动测试
采用环境随机激励法测试桥梁的自振特性,拾振器采用4只DSP0.5-2-H(V)型超低频位移传感器,拾振范围≥0.1 Hz;动态数据采集使用美国产WaveBook216a型信号采集分析系统,桥跨结构典型横向和竖向脉动响应频谱图见图10。
该桥竖向1阶频率为3.36 Hz,横向前两阶频率分别为 2.17,3.69 Hz。

图10 实测频谱Fig.10 Measured spectrogram
3.3 有限元模型改进
依据图纸建立理想有限元模型,经动力分析得其竖向1阶频率为5.02 Hz,横向前两阶频率分别为1.83,5.71 Hz。
结合桥梁实际状态,发现两端支点与桥台间采用橡胶支座,与理想有限元模型中的固定约束不符,造成计算频率偏大。考虑改用COMBIN14单元模拟支座横向、竖向刚度,将刚度系数视为设计参数,计算模型如图11。

图11 计算模型Fig.11 Calculation model
根据以上计算模型建立如图12的有限元模型。

图12 有限元模型Fig.12 Finite element model
3.4 模型修正
将支座的横向、竖向刚度作为设计参数,根据多次试算所得规律与工程经验,确定参数取值范围:横向刚度的最小值=1 720 N/mm,最大值=5 200 N/mm;竖向刚度的最小值=1 720 N/mm,最大值=5 200 N/mm。选用U30(303)均匀设计表形成3因素30水平均匀试验,共计30个试验样本[8]。
根据试验样本数据,采用最小二乘法回归所得各阶响应面系数回归值如表6。
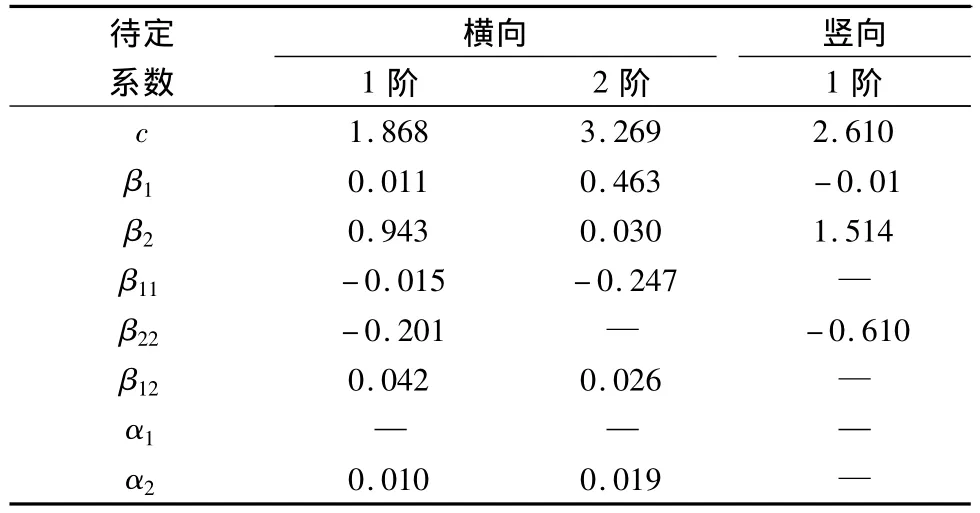
表6 待定系数最小二乘解Table 6 Least square solution of parameters
各阶响应面有效性检验值如表7。
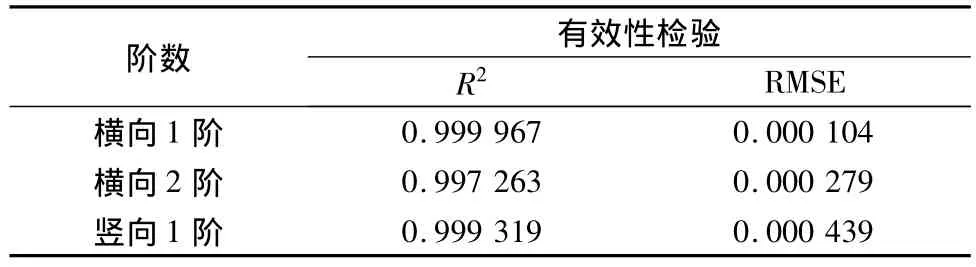
表7 响应面有效性检验Table 7 Validity tests of the response surfaces
根据式(8)建立目标函数:

通过基于自然选择的混合粒子群算法对目标函数优化求解,迭代过程如图13。
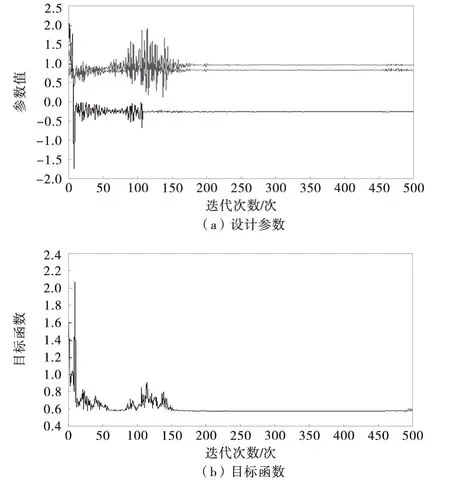
图13 迭代收敛曲线Fig.13 Iteration curves of the optimization
优化求解经历迭代150次左右达到收敛,得到设计参数支座横向刚度2 547.11 N/mm,支座竖向刚度3 746.12 N/mm。优化值均在样本范围内,将其代回有限元模型,通过模态分析得到竖向一阶模态频率为3.37 Hz,与实测值相差仅0.30%,表明修正后有限元模型的整体动力特性与实际桥梁更加符合。
4.5 动力响应验证
现场使用25T载重汽车分别以5,10,20 km/h速度通过桥梁。受现场条件限制,车辆到达甘洛端后就地停留,未驶出桥面。实测跨中测点动挠度曲线如图14。
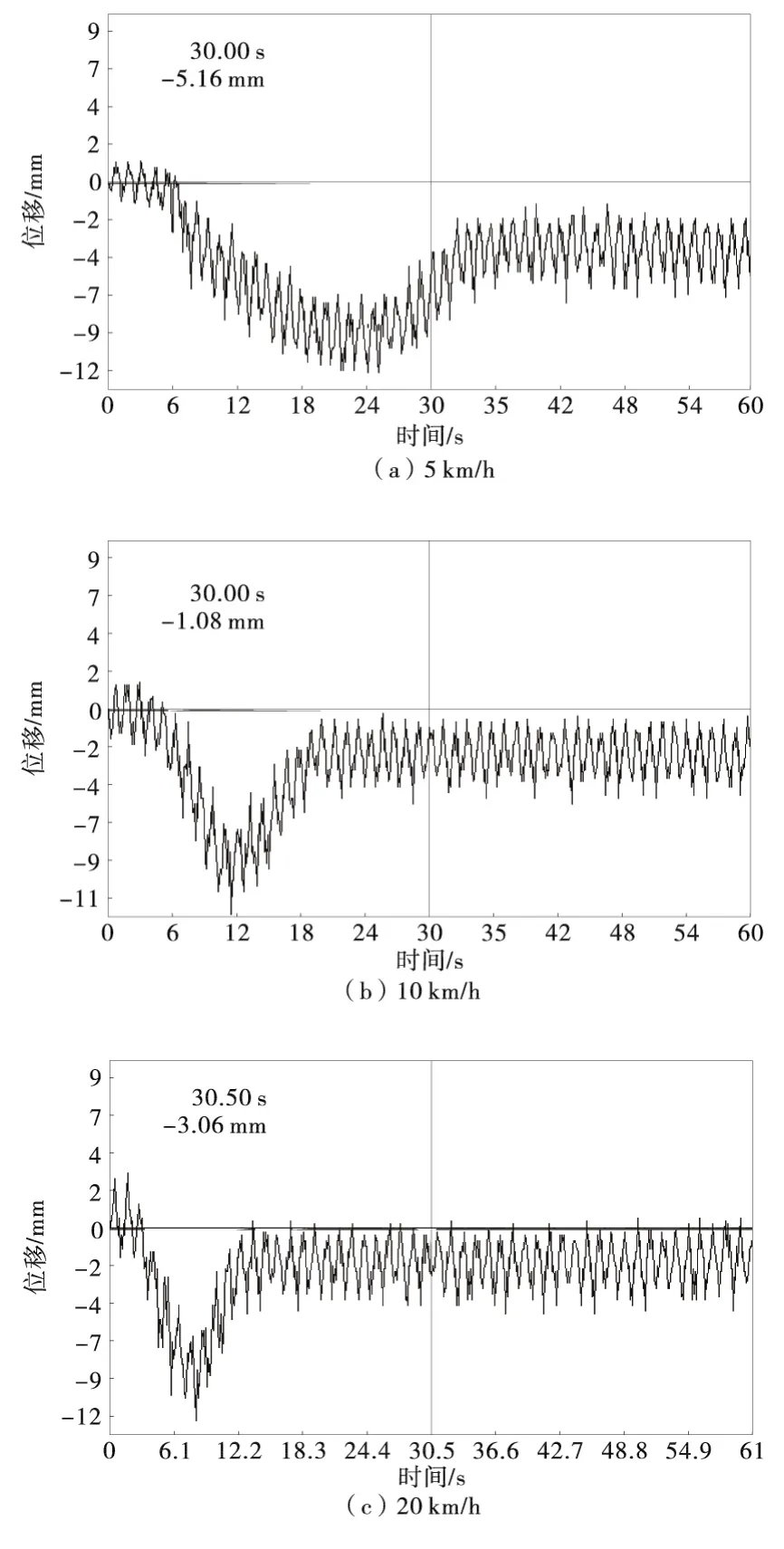
图14 跨中实测动挠度曲线Fig.14 The measured dynamic deflection curves of the mid-span
在修正后有限元模型的基础上,采用ANSYS瞬态动力学分析对桥梁动力响应进行仿真计算,使用与现场试验相同的荷载,通过桥梁后,保持端部荷载不撤除,模拟现场实测过程,得到跨中动挠度曲线如图15。
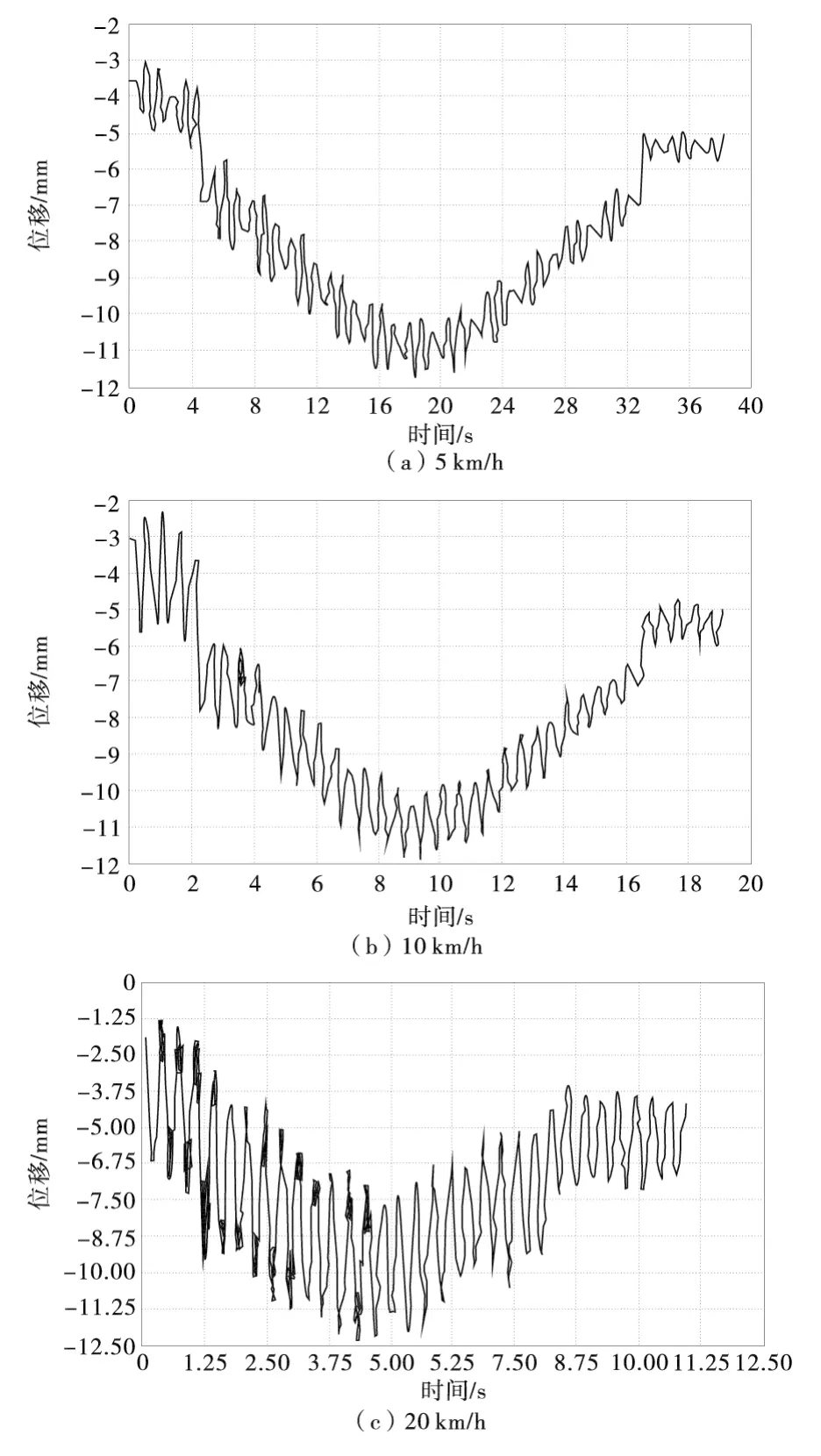
图15 跨中仿真动挠度曲线Fig.15 The simulation dynamic deflection curves of the mid-span
分别从修正前、修正后的有限元仿真分析结果中提取跨中动挠度最大值,与实测值相比较,相对误差见表8。
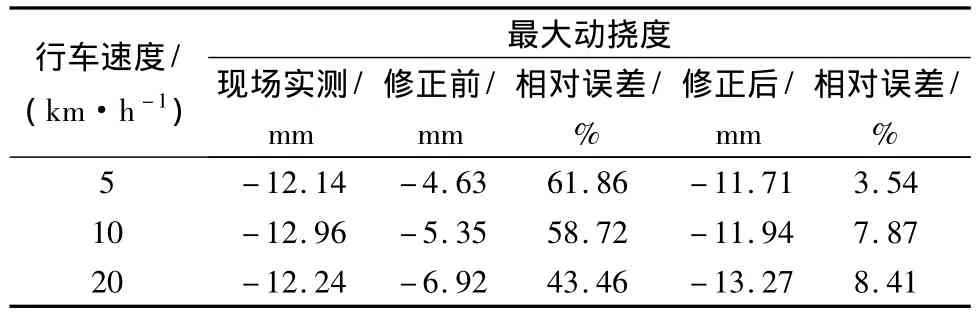
表8 最大动挠度对比Table 8 Comparison of the maximum dynamic deflection
表8表明,经修正后的桥梁有限元模型的动力响应与实际结构相近,表明其能较准确地反映出结构的真实动力特性,可用于日后的优化设计、健康监测、结构动力响应再分析等。
4 结论
1)2阶式-高斯组合径向基函数响应面具有较强的非线性适应性,求解过程中,能准确再现设计参数-响应值之间的复杂关系,利用其可避免有限元模型的反复调用。
2)设计参数的选取应根据工程实际情况而定,必要时可对有限元模型进行局部改进,使其更接近于实际结构,从而产生新的设计参数作为修正对象。
3)文中残差型目标函数对各自变量平等对待,优化过程中自动优先考虑残差绝对值较大的自变量,后续对于重要自变量未被优先考虑的情形,可设置加权值予以改善。
4)文中方法修正所得有限元模型能有效再现原结构的动力特性,在初始模型与设计参数合理的前提下,既使实测数据有限,也可得到准确的有限元模型。
[1] Wei Xinren,Hua Bingchen.Finite element model updating in structural dynamics by using the response surface method[J].Engineering Structures,2010,32(4):2455-2465.
[2] Lu Deng,Cai C S.Bridge model updating using response surface method and genetic algorithm [J].Journal of Bridge Engineering,2010,15(5):553-564.
[3] 周林仁,欧进萍.基于径向基函数响应面方法的大跨度斜拉桥有限元模型修正[J].中国铁道科学,2012,33(3):8-15.Zhou Linren,Ou Jinping.Finite element model updating of longspan cable-stayed bridge based on the response surface method of radial basis function [J].China Academy of Railway Sciences,2012,33(3):8-15.
[4] 孔宪仁,秦玉灵,罗文波.基于改进高斯径向基函数响应面方法的蜂窝板模型修正[J].复合材料学报,2011,28(5):220-227.Kong Xianren,Qin Yuling,Luo Wenbo.Improved Gaussian RBF response surface method-based model updating for the honeycomb sandwich panel[J].Acta Materiae Compositae Sinica,2011,28(5):220-227.
[5] 秦玉灵,孔宪仁,罗文波.基于径向基函数响应面的机翼有限元模型修正[J].北京航空航天大学学报,2011,37(11):1465-1470.Qin Yuling,Kong Xianren,Luo Wenbo.Finite element model updating of airplane wing based on Gaussian radial basis function response surface[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(11):1465-1470.
[6] 张松涵.基于组合函数动力响应面的桥梁有限元模型修正[D].成都:西南交通大学,2013.Zhang Songhan.Bridge Finite Element Model Updating Based on Dynamic Response Surface of Combination Function[D].Chengdu:Southwest Jiaotong University,2013.
[7] Tshilidzi Marwala.Finite-Element-Model Updating Using Computational Intelligence Techniques[M].New York:Springer,2010.
[8] 方开泰.均匀设计与均匀设计表[M].北京:科学出版社,1994.Fang Kaitai.Uniform Design and Uniform Design Table[M].Beijing:Science Press,1994.
[9] Anula Khare,Saroj Rangnekar.Particle swarm optimization:A review [J].Applied Soft Computing Journal,2012(6):467-484.
[10] 龚纯,王正林.精通MATLAB最优化计算[M].2版.北京:电子工业出版社,2012.Gong Chun,Wang Zhenglin.Proficient in Optimization Calculation of MATLAB[M].2nd ed.Beijing:Publishing House of Electronics Industry,2012.
