恢复古水动力场定量研究油气运聚

李忠权，彭 戟，应丹琳，应文峰，，李 应，龙 伟

（1.油气藏地质及开发工程国家重点实验室（成都理工大学），成都610059；2国土资源部构造成矿成藏重点实验室（成都理工大学），成都610059；3.中国石油 西南油气田分公司，成都610041；4.密苏里科技大学 地质与地球物理学院，美国615401）

古水动力场是指各地质历史时期的古水势面貌，研究和恢复古水动力场的目的就是了解油气运移富集区块，以便更好地为勘探服务［1－3］。油气运移一般包括初次运移和二次运移两个过程：初次运移为油气首先从生油层同水一起进入储集层，进而在储集层中由油、气、水高势区向低势区进行二次运移，并在运移道路上的圈闭中油气聚集成藏；而后期水动力场变化，也会造成已形成油气藏散失和重新运移 。因此可见，古水动力条件与油气运移及聚集密切相关。

长期以来，许多学者致力于油气运聚的定量研究，但方法不一［4，5］。本文着重介绍三维古水动力场恢复的理论基础及解决方法，以此为基础，将油气初次运移与二次运移联系在一起，对油气运聚作出定量评价，其结果对指导油气勘探有较大意义。

1 数理模型的建立

建立此模型有如下假设：（1）储层无区域性排水断裂；（2）压实水量是渗流层唯一补给源；（3）固体颗粒压缩性远小于岩石压缩性，所以认为颗粒体积不变。

在渗流区域取一个无限小立方体，如图1所示，根据质量守恒定律

式中：vx、vy、vz分别为X、Y、Z方向的渗流速度分量；W为单位时间、单位面积压实水量；δ为储层厚度；q为渗流层孔隙度；ρ为液体密度；t为时间。

图1 计算水动力单元示意图Fig.1 Sketch map of calculating hydraulie unit

我们在化简此式时，有两点与普通水文不同：（1）储层上覆总应力是变化的，据泰萨基公式

式中：σ总为总应力；σ有为有效应力；p为水压力。

则 dσ有＝dσ总－dp

（2）储层的海拔高度是不断变化的，即

式中：H为水头高度；Z0为储层距海平面的距离。

式中：β为液体体积压缩率。

最后推导出古水动力场数理方程

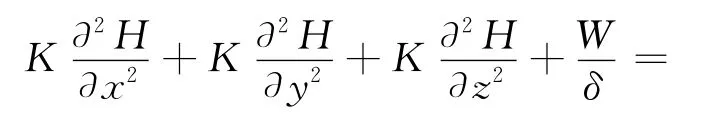
式中：K为渗透系数；Ss为储水率，Ss＝ρg（α＋qβ）。

2 恢复各地质时期古水动力场

古水动力场数理方程（1）是二阶偏微方程。如此复杂的方程，要求出它的解析解是不可能的。为此，可采用有限单元法，解出水头的数值解［6］。

用有限单元法解出古水头的关键是边界性质确定及参数的给出。

2.1 边界的确定

经反复对比计算，选用了导水系数和压实水量相结合的办法确定。

导水系数的定义是：渗透系数×渗流层厚度，它反映渗流层的导水能力。一般情况下地层往往由导水系数小的区域流向导水系数大的区域，因此可在导水系数等值线图上将研究区划分成几个区，如图2；然后对每个区进一步划分成若干个三角形单元，如图3。这样，根据各区域的压实水量等于各三角单元的总排泄水量的原则，利用各控制点的压实水量，近似求出边界的排泄量。

2.2 参数的确定

（1）垂直总应力（σ/Pa），按下式计算

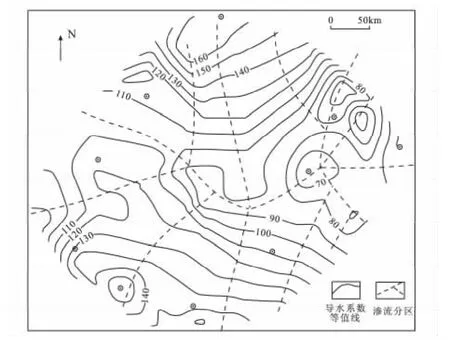
图2 用导水系数等值线图划分渗流区域Fig.2 Diagram showing the vadose zones devided by the contour map of transmissivity coefficients

图3 单元划分示意图Fig.3 Sketch map of subdivision

式中：δi为i层厚度（m），由压实计算获得；qi为i层孔隙度，由压实计算获得；ρsi为i层岩石骨架密度；ρwi为i层孔隙水的密度。

（2）岩石骨架压缩率（α/Pa－1）

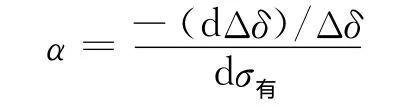
式中：δ为岩石厚度（m），Δδ及d（Δδ）都可根据压实计算得到。

有效应力σ有，是采用叠代法求出：首先将前期埋深比前期水头值求出压力系数，用该值乘以后期埋深，则得该期的近似水头值，并换算成水压，又有σ有＝σ总－p，可求出σ有1，求出近似的岩石骨架压缩率α1。用该α1值作计算求出近似水头值H1，将其换算成近似地层压力，代入σ有＝σ总－p，求得新的σ有2，进而求得新的σ有和水头值H2。如果叠代前后水头值的误差平均大于10 m，需再次进行叠代，直到平均误差小于10m为止，其α值就比较准确。一般叠代2次，最多3次。

（3）液体压缩率（β/Pa－1），按地层平均温度和平均矿化度查表获得。

（4）孔隙度（q），由压实计算可得。

（5）单位时间、单位面积压实总水量［W/（m3·Ma－1），包括上、下泥岩挤入储层压实量］，由压实计算可得。

（6）储层厚度（δ/m），由压实计算可得。

（7）Δt为各阶段经历的间隔时间（Ma）。

（8）K为渗透系数（m/Ma），K＝kρg/ν（其中k为渗透率）。

（9）地层水运动黏度（ν/Pa·s），据含盐量、地温，查表获得。

3 用恢复的古水动力场对油气运聚进行定量分析

用上述方法，就可以恢复各个地质时期的古水动力场（图4）。在此基础上，可以对油气二次运聚的演变过程进行定量分析。

图4 四川盆地侏罗系阳新统水动力图Fig.4 Hydrodynamic map of Yangxin in Jurassic in Sichuan Basin

a.二次运移同油气在地下的相态有密切关系，只有计算了各控制点在各个地质时期的气油比、气水比之后，再同油气在地下的溶解度比较，才能作出油气的相态判断。而气油比、气水比、油气在地下溶解度的定量解，都要以古水动力场为基础。首先根据各期的水头等值线图所反映的流向来计算各点的单宽油、气、水量。它反映了油、气、水在储层中运移量的动态。利用各地质时期的单宽流量进一步计算出各期的气油比、气水比；再按各地质时期目的层的水头值、埋藏深度、地温梯度，根据一定的公式计算出气在原油中的地层水的溶解度。这样，由上所求烃的溶解度及实际气油比、气水比可计算出相态值，其值大小反映了某种烃类的相态。当相态值小于或等于0，说明地层中仅存在油（含溶解气）两相；当相态值大于0或等于1时，说明地层中存在饱和气体的油相和含溶解气或被气体饱和的水两相；当相态值大于1，则有饱和气的油相、饱和气的水相以及饱和态的游离气相三相存在。可见相态值可作为判断各个时期油气在储层中的相态准则，所以它对油气运聚有重要意义。

b.在油气全部溶解于地层水时，其运移主要受水势控制。当出现油、气、水中的2种以上相态时，其运移主要受水动力和浮力的合力作用，即流体自身势的控制。由水头值，根据哈伯特流体势的公式，计算出油势和气势。

c.由各地质时期的相态值、油气势及油气流量的展布特征，结合古构造的演化，可对各地质时期油气聚集程度作出定量评价。整个过程见图5。

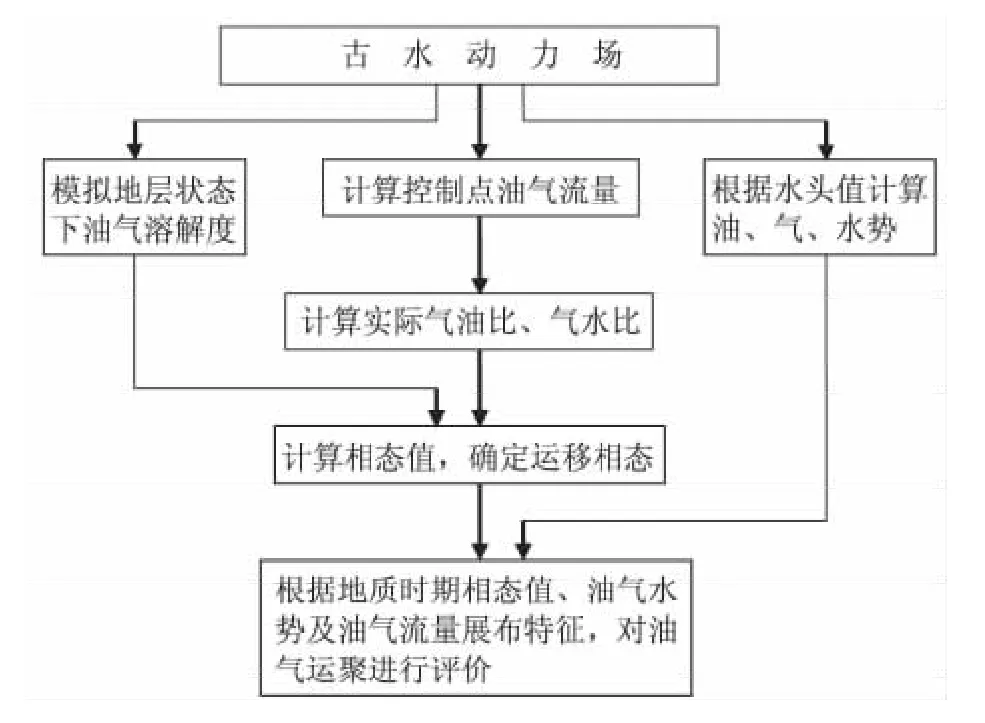
图5 油气评价数值模拟流程图Fig.5 Flow chart of numerical simulation of oil and gas evaluation

4 四川盆地阳新统油气运聚分析

四川盆地二叠系阳新统是一套生物繁盛的碳酸盐台地相沉积，从晚二叠世直到第三纪沉积期，阳新统一直处于深埋环境，至喜马拉雅第Ⅱ幕达到最大埋深，根据地质资料和地质发展史的分析，可以将其划分为8个期：晚二叠世、中三叠世、中三叠世、晚三叠世、早侏罗世、中侏罗世、晚侏罗世、白垩纪—第三纪，用上述方法，以区内46口钻井为计算节点对各期古水动力场、油气运聚进行模拟分析，编制出阳新统8个地质时期的古水动力图、油气流量及相态图、油气势图及聚集分区图（因篇幅有限，仅附1张图，见图6），展示了白垩纪－早第三纪有机质达到成熟阶段，处于成气高峰期，四川南部以乐山－泸州隆起为中心的低势区为富气区，川东丰都－垫江－大竹一带也为含气区，其聚集分区的展布同目前勘探效果较为一致，为勘探区带优选提供重要的指示。

图6 四川盆地白垩纪至早第三纪阳新统油气势及聚集分区图Fig.6 Map of the potential energy and the accumulation partition of oil and gas in Yangxin from Cretaceous to early Tertiary in Sichuan Basin

5 结论

a.以压实为机制所建立的压实流古水动力方程，采用盆地模拟技术，可重现目的层古水动力场，编制的油势、气势、油气单宽流量等反映油气运移的等值线图，可成为判断油气运移方向的直观方法。

b.四川盆地二叠系阳新统自白垩纪－早第三纪以来，南部以乐山－泸州隆起为中心的低势区为富气区，东部丰都－垫江－大竹一带也为含气区。

［1］楼章华，金爱民，田炜卓，等.论陆相含油气沉积盆地地下水动力场与油气运移、聚集［J］.地质科学，2005，40（3）：305－318.Lou Z H，Jin A M，Tian W Z，etal.Origin and evolution of hydrocdynamics and the migration，accumulation of petroliferous sedimentary basins［J］.Chinese Journal of Geology，2005，40（3）：305－318.（In Chinese）

［2］王震亮，陈荷立.试论古水动力演化的旋回性与油气的多期次运聚［J］.沉积学报，2002，20（2）：339－344.Wang Z L，Chen H L.A view on cycles of paleohydrodynamics evolution and phases of hydrocarbon migration and accumulation［J］.Acta Sedimentologica Sinica，2002，20（2）：339－344.（In Chinese）

［3］杨绪允.论含油气盆地地下水动力环境［J］.石油学报，1989，10（4）：27－34.Yang X Y.On the underground hydrodynamic environment in an oil-gas basin［J］.Acta Petrolei Sinica，1989，10（4）：27－34.（In Chinese）

［4］曾溅辉.台北凹陷地下水动力特征及其对油气运移和聚集的影响［J］.沉积学报，2000，18（2）：273－278.Zeng J H.Hydrocarbon characteristics and its effect on oil-gas migration and accumulation in Taibei depression［J］.Acta Sedimentologica Sinica，2000，18（2）：273－278.（In Chinese）

［5］康永尚，郭黔杰.论油气成藏流体动力系统［J］.地球科学，1998，23（3）：281－284.Kang Y S，Guo Q J.On oil and gas migration and accumulation fluid dynamic systems［J］.Earth Science，1998，23（3）：281－284.（In Chinese）

［6］薛禹群，叶淑君，谢春红.多尺度有限单元法在地下水模拟中的应用［J］.水利学报，2004，35（7）：7－13.Xue Y Q，Ye S J，Xie C H，etal.Application of multi-scale finite element method to simulation of groundwater flow［J］.Journal of Hydraulic Engineering，2004，35（7）：7－13.（In Chinese）