基于系统动力学的弹药保障优化分析
2015-01-04刘洪坤赵建江朱皖松
刘洪坤,赵建江,朱皖松
(装甲兵学院,安徽蚌埠233050)
基于系统动力学的弹药保障优化分析
刘洪坤,赵建江,朱皖松
(装甲兵学院,安徽蚌埠233050)
基于系统动力学原理和方法,在分析战时弹药保障系统控制机理和各要素间的因果关系的基础上,建立了战时弹药保障系统动力学仿真模型,利用VENSIM仿真平台对模型进行模拟,得出了在不同影响因素条件下的战时弹药保障系统的运行规律,分析了不同要素对战时弹药保障系统弹药存储的影响,提供了一种预测弹药保障系统初始存储量和期望存储量最小值的方法。
弹药保障控制,系统动力学,仿真模拟,优化分析
0 引言
弹药保障是后勤保障的重要内容,在正确的时间将弹药配送到正确的位置是保持部队战斗力的关键环节。弹药从生产基地到作战部队,一般需经历生产仓储中心——战区储存地域——军储存地域——弹药补给站——弹药中转站——作战部队的流程。从上一级保障单位向下一级保障单位供应弹药,应先由下级单位提出弹药需求,而后由上级保障单位向需求单位实施供应。但从下级单位提出需求到上级单位实施供应,直到弹药供应到作战部队,必然存在着时间延迟,也就是说,弹药并不一定在正确的时间供应到作战部队。因此,本级保障单位在何时提出弹药需求,将对上级保障单位能否及时供应弹药、准确保障作战部队弹药需求有直接影响。
本文抛开传统的保障方式,假设面向一定规模的作战部队,设立一个弹药保障中心,由该保障中心向上级保障部门(弹药库、保障中心等)提交弹药需求(订货),集中存储弹药,根据作战部队弹药需求及时向各需求点输送弹药。该保障中心运行的关键是弹药存储系统要有足够的存储量以保证各作战部队的需求,同时为减小上级保障部门的保障压力、保障中心运行费用和风险,又要尽量减少存储量。因此,必须对其存储进行科学的管理。传统的存储计算是通过存储论模型来解决的,但是计算复杂、不直观、对历史数据的数量和准确性的依赖强,并且无法追踪系统中变量间相互影响与作用的逻辑关系与数量关系。系统动力学可以实现动态追踪、反映系统行为,并且直观、易于理解、对历史数据的依赖和要求也较低。能够有效地解决保障中心存储的确定与控制问题。
本文利用系统动力学的定性与定量分析相结合的原理和方法建立保障中心控制系统动力学模型,利用系统动力学仿真平台VENSIM软件提供的模拟环境,对模型进行仿真和结果分析。
1 保障中心弹药存储控制因果关系分析
因果关系的确定能把复杂系统的问题较为简单地表示出来,因果关系分析是系统动力学建模的基础,是对系统内部结构关系的一种定性描述,结合分析保障中心存储控制各因素之间的相互影响关系,可得到战时弹药保障中心存储控制因果关系图。
图1中箭线表示各要素之间的因果关系,标注+的表示正的因果关系,标注-的表示负的因果关系,保障中心弹药存储控制因果关系分析直观地表示出了保障中心弹药存储控制系统中各因素间的相互影响关系。

图1 保障中心弹药存储控制因果关系分析
图中有两个因果反馈回路,一是作战部队弹药量弹药补充保障中心弹药出库作战部队弹药量,由于弹药消耗会使作战部队弹药量减少,为作战部队弹药量达到期望量就要增加弹药补充,随着弹药补充量的增加,保障中心弹药出库量也相应增大,进而使作战部队弹药量增多;二是保障中心弹药存储量存储调节订货上级保障单位发货保障中心弹药存储量,当保障中心有弹药出库时,保障中心弹药存储量减少,经过存储调节、订货、上级保障单位发货,使保障中心的弹药存储量增加,实现了自调整。这是两个负反馈回路,负反馈回路使回路中各变量趋于稳定的特点,使得保障中心弹药存储控制具有可调节性,这些反馈回路客观地反映了保障中心弹药存储控制的机理。
2 保障中心弹药存储控制系统动力学模型
一个保障中心保障的需求点可能有多个,在本文中假设有3个需求点。在保障中心弹药存储控制因果关系图的基础上,建立保障中心弹药存储控制系统动力学模型,利用系统动力学仿真平台绘制其流图如图2所示。

图2 保障中心弹药存储控制系统动力学流图
模型中有保障中心弹药存储量、各需求点的弹药量4个流位变量;保障中心的出库率和进库率、各需求点的弹药到达率和消耗率8个流率变量;信息延迟时间,保障中心的进库延迟时间,各需求点的弹药消耗量,保障中心及各需求点的库存调节时间、期望库存量、库存调节率等辅助变量来描述各自所影响的流率变量。
3 模型仿真与分析
假设在仿真模拟中,上级保障单位能始终满足保障中心的需求,保障中心向各需求点输送弹药无时间延迟,取各需求点的调节时间均为1天,保障中心的调节时间为3天、进库延迟时间为2天、信息延迟时间为2天,保障中心、A、B、C3个需求点的弹药初始量分别为400、100、100、100单位,保障中心、A、B、C3个需求点的期望弹药量分别为500、90、110、100单位,A、B、C3个需求点每天的弹药消耗量分别为35、45、40单位。利用所建模型进行模拟,可以得到保障中心出库率、进库率、弹药需求量,保障中心、A、B、C3个需求点的弹药量变化曲线如下页图3所示。
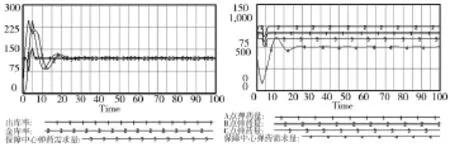
图3 弹药量变化曲线
图中纵坐标范围为0~300的是出库率、进库率、保障中心弹药需求量的变化曲线;纵坐标范围为0~150的是A点弹药量、B点弹药量、C点弹药量的变化曲线;纵坐标范围为0~1 000的是保障中心弹药存储量的变化曲线(下面各图相同)。
3.1 进库延迟时间对弹药库存控制的影响
将进库延迟时间改为1天,利用所建模型进行模拟,可以得到保障中心出库率、进库率、弹药需求量,保障中心、A、B、C 3个需求点的弹药量变化曲线如图4所示。
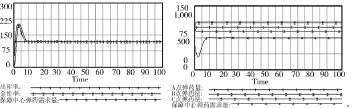
图4 1天弹药量变化曲线
将进库延迟时间改为3天,利用所建模型进行模拟,可以得到保障中心出库率、进库率、弹药需求量,保障中心、A、B、C3个需求点的弹药量变化曲线如图5所示。
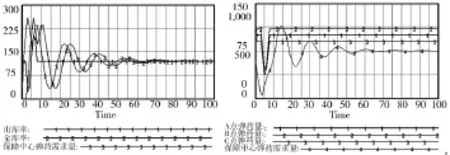
图5 3天弹药量变化曲线
将进库延迟时间改为4天,利用所建模型进行模拟,可以得到保障中心出库率、进库率、弹药需求量,保障中心、A、B、C3个需求点的弹药量变化曲线如图6所示。

图6 4天弹药量变化曲线
3.2 库存调节时间对弹药库存控制的影响
将进库延迟时间改为2天,利用所建模型进行模拟,可以得到保障中心出库率、进库率、弹药需求量,保障中心、A、B、C3个需求点的弹药量变化曲线如图7所示。
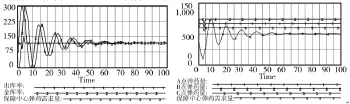
图7 2天弹药量变化曲线
将进库延迟时间改为4天,利用所建模型进行模拟,可以得到保障中心出库率、进库率、弹药需求量,保障中心、A、B、C3个需求点的弹药量变化曲线如图8所示。

图8 4天弹药量变化曲线
3.3 预测保障中心初始弹药初始量的最小量
在已知保障中心期望存储量、进库延迟时间、信息延迟时间、各需求点的弹药消耗量、保障中心及各需求点的库存调节时间、各需求点期望库存量、各需求点的初始弹药量的情况下,可以利用该模型预测保障中心初始弹药量的最小值。表1给出了保障中心期望存储量和进库延迟时间不同时保障中心初始弹药量的最小值。

表1 期望存储量与延迟时间
分析表中数据可以看出:同样条件下进库延迟时间越小保障中心初始弹药量的最小值越小、保障中心期望存储量越小保障中心初始弹药量的最小值越大。
在本文的基本条件下,通过改变参数进行多次模拟得出:当进库延迟时间为3天时,保障中心初始弹药量最小值为190,此时保障中心期望存储量至少为540;当进库延迟时间为2天时,保障中心初始弹药量最小值为80,此时保障中心期望存储量至少为420;当进库延迟时间为1天时,保障中心初始弹药量最小值为0,此时保障中心期望存储量至少为490。
3.4 预测保障中心期望存储量最小量
在已知保障中心初始弹药量、进库延迟时间、信息延迟时间、各需求点的弹药消耗量、保障中心及各需求点的库存调节时间、各需求点期望库存量、各需求点的初始弹药量的情况下,可以利用该模型预测保障中心初始弹药量的最小值。表2给出了保障中心初始弹药量和进库延迟时间不同时保障中心初始弹药量的最小值。
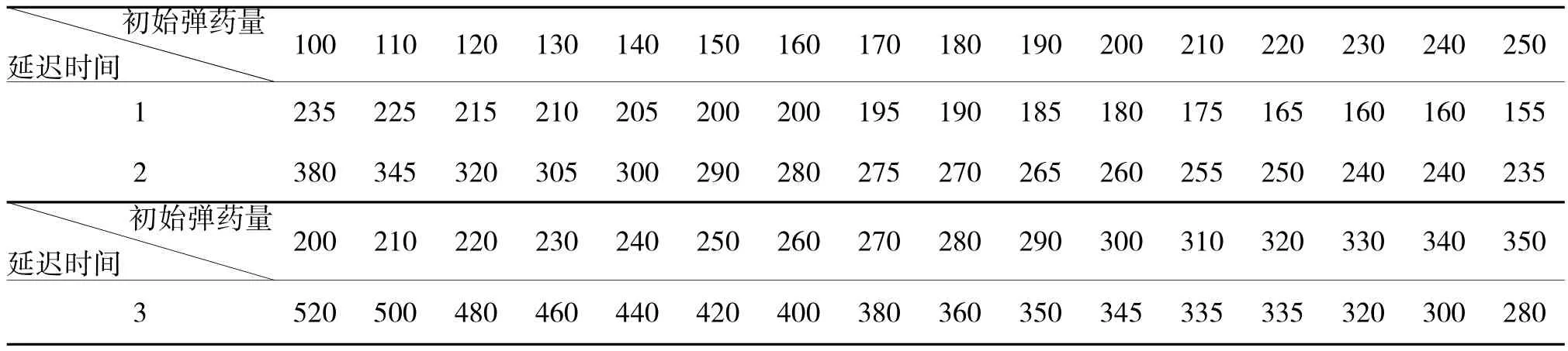
表2 延迟时间不同与初始弹药量
分析表中数据可以看出:同样条件下进库延迟时间越小保障中心期望存储量越小,保障中心初始弹药量的最小值越小保障中心期望存储量越大。
通过改变参数进行多次模拟得出:当进库延迟时间为3天时,保障中心期望存储量最小值为149,此时保障中心初始弹药量至少为1 120;当进库延迟时间为2天时,保障中心期望存储量最小值为122,此时保障中心初始弹药量至少为1 090;当进库延迟时间为1天时,保障中心期望存储量最小值为120,此时保障中心初始弹药量至少为490。
在模拟结果中,保障中心初始弹药初始量和期望存储量达到最小时,与其对应的期望存储量和初始弹药初始量的最小量都偏大,因此,当保障中心初始弹药初始量和期望存储量达到最小时,整个保障中心的效益不一定最优,还要综合分析影响保障中心运行效益的其他因素,来确定最优的初始弹药量和期望存储量。
4 结束语
本文利用系统动力学原理和方法,分析了战时弹药保障系统控制因果关系,构建了战时弹药保障系统控制系统动力学仿真模型,通过对模型的仿真模拟,得出了改变进库延迟时间、库存调节时间等影响因素条件下,弹药保障系统存储控制的运行规律,动态、真实地反映了实际系统。提供了一种预测弹药保障系统初始存储量和期望存储量最小值的方法,可以为战时根据不同的作战情况下弹药保障管理和决策提供一定的科学参考。当系统结构发生变化时,模型还可相应修改以适应新的系统。
[1]王其蕃.系统动力学[M].北京:清华大学出版社,1994.
[2]贾仁安.系统动力学——反馈动态性复杂分析[M].北京:高等教育出版社,2002.
[3]袁旭梅.“啤酒游戏”的系统动力学分析[J].价值工程,2007(4):29-30.
[4]吴隽.基于系统动力学的牛鞭效应仿真分析[J].物流科技,2008(2):36-37.
Optimized Analysis of Ammunition Support Based on System Dynamics
LIU Hong-kun,ZHAO Jian-jiang,ZHU Wan-song
(Armored Force Institute,Bengbu 233050,China)
The system dynamics model of ammunition support at war time is built based on the analysis of its control mechanism and relations among related factors using system dynamics method. The model is simulated on VENSIM platform,which finds the function laws of ammunition support at war time with different factors.The influence brought to storage of ammunition support at war is analyzed,and an approach to forecasting the minimum value of initial and expected storage of ammunition support system is proposed.
ammunition support control,system dynamics,simulation,optimized analysis
TJ630
A
1002-0640(2015)12-0163-04
2014-11-13
2015-01-18
刘洪坤(1981-),男,河南淮阳人,硕士研究生。研究方向:兵种战术、作战效能评估。
