基于滑模控制方法的航空发动机控制系统改进设计

徐清诗，郭迎清

（西北工业大学动力与能源学院，西安710129）

基于滑模控制方法的航空发动机控制系统改进设计

徐清诗，郭迎清

（西北工业大学动力与能源学院，西安710129）

为改善传统基于线性控制方法（PID控制）设计航空发动机控制系统在极限保护方面的不足，提出利用非线性控制理论——滑模控制取代原有控制系统中的线性控制器，设计了发动机稳态控制器与基于max-min控制逻辑的极限保护器的综合系统。与传统PID控制方法的控制效果相比较，滑模控制方法可在保证发动机不超限的情况下充分发挥发动机潜能。讨论了边界层厚度等因素对滑模控制抖动的影响。采用滑模方法设计的控制器在硬件在回路平台（H IL）上通过了仿真验证，满足实时性要求。

滑模控制；PID控制；max-min选择逻辑；硬件在回路仿真；航空发动机

0 引言

滑模控制作为1种强鲁棒性非线性控制方法在飞行器制导与控制[1]、机器人控制[2]等领域已有广泛应用。但由于滑模控制方法控制具有不连续性，在实际系统应用中因系统惯性等因素不可避免地出现高频抖振现象[3]。早期的航空发动机控制系统受机载计算机计算能力低下以及滑模控制在抑制抖振方面研究不成熟的影响，滑模控制方法未能应用于航空发动机控制系统中。近几年，美国NASA[4]和克利夫兰州大学的Hanz教授等提出利用滑模控制方法改进现有极限保护控制中的max-min逻辑[5-7]，取得一定成果。

在对航空发动机加、减速计划线进行设计时已充分考虑超温、超转、喘振裕度等因素[8]。而发动机超限在飞行条件发生剧烈变化等情况下也极易发生，因此，有必要研究在稳态控制作用下发动机不超限问题。Max-min选择逻辑作为1种典型的管理机制[9]，通常在发动机控制变量只有1个，而被控制量有多个时（用于控制发动机转速和限定系统在不同设计点均能保持在规定的限制范围内），能显著发挥作用。本文正是在max-min选择逻辑的基础上设计了基于滑模控制方法的极限保护控制器与稳态控制器的综合系统。

1 稳态控制器设计

稳态控制的目的是在相对较长的周期内调节发动机的性能，使其接近期望工作状态[10]。稳态控制又称设定点控制，稳态工作点有时被称为设定点，对应于由发动机产生的1个固定的功率状态，该状态由发动机转速或增压比控制。

1.1 理论分析

为简要分析滑模控制方法，首先采用小偏离线性化得到发动机某个稳态点模型，对控制器应用滑模控制。以发动机燃油流量WF为控制输入，控制风扇转子转速Nf。由于发动机稳态点模型的传递函数中分子是高于2阶的，利用传统的求取等效控制方法设计滑模控制器时，输入的高阶微分项在控制计算时有诸多不便，本文采用积分式滑模控制方法[11]对发动机进行控制。

假定发动机的稳态点模型用状态空间的形式为

式中：x=[ΔNfΔNc]T，分别表示风扇转子转速偏移量和核心转子转速偏移量；被控对象的输入u为发动机燃油流量偏移量ΔWF；输出y为风扇转子转速偏移量ΔNf。

设发动机的期望转速偏移量为yexp。由于A为n×n非单一的矩阵，并且（A，B）可控。定义1个系统的辅助输出为

式中：G用于表征被设计滑动系数的1个向量。

引入s的微分，根据滑模控制理论设计实现条件为

定义xa为扩展状态，ur为控制速率ur=。那么，控制速率可描述为

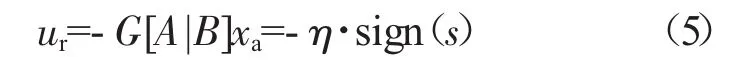
对上式进行积分即为滑模控制的控制律。

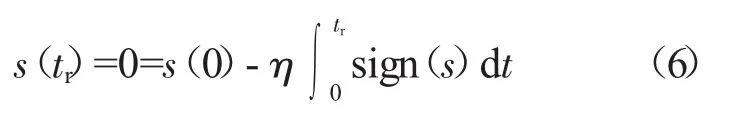
对于理想的滑模控制，s的符号一般是恒定的。sign（s）=sign（s（0）），利用该式将上式的积分化简求解可得

实践中，若想达到期望的调节时间，可通过调节来实现。

当系统到达滑模模态s=0，必有y*=。由此，通过u=-Gx与被控对象状态相关联，可得

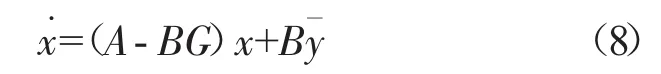
式（8）是反映了滑模动态与原发动机模型相关联的降阶关系式。如果A-BG是稳定的，那么就能实现稳定状态。其中稳定状态为，由此计算

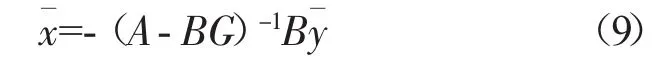
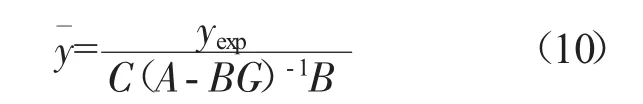
根据上述理论分析，可推得滑动方程为

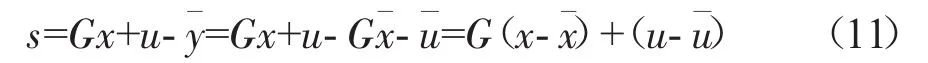
1.2 仿真实例

根据上述理论分析，将简化的设计应用到控制风扇转速问题中。仿真中为减弱抖振，将式（3）中的符号函数用饱和函数替代，这个设计包含3个要素：

（1）选择G决定滑模动态的特征值；

（2）选择切换增益η的值以满足调节时间要求，选择边界层厚度φ以削弱抖振影响；

首先可直接得到极点位置，因A-BG为2阶，极点可以反映理想时间常数和阻尼值。令阻尼比ζ=0.7，自然频率ωn=11.43 rad/s，可计算极点位置为-8± 8.1616i，其中相关的调节时间为0.5 s。通过在Matlab中编写程序得到G值，根据Matlab计算结果取G= [0.1405-0.0318]。

设ΔNf的期望值为340，根据式（10）计算可得=34.4252。根据式（7）可得

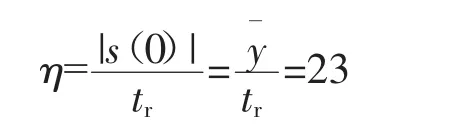
根据式（5），可在Matlab/Simulink下搭建模型。

稳态控制ΔNf的输出响应如图1所示。为使仿真结果更为明显，图1中的输出未考虑设计点的值，即图1为风扇转子转速偏移量ΔNf的响应输出，其期望目标值为340；滑模变量s如图2所示，其目标值为0。

图1 稳态控制ΔNf的输出响应

图2 稳态控制s的输出响应

1.3 结果分析

仿真结果如图1～3所示。从图1可见，ΔNf的响应结果略有超调，这是因为滑动变量s直接控制的量是等效输出y*，而不是输出y。从图3可见，y*在到达稳态值后就一直稳定在该区域，满足了滑动模态的特性。

图3 稳态控制y*的输出响应

由式（11）可见超调量与调节时间η有关，这是因为定义滑动变量s不仅与状态x有关，也与输入u有关。当η增大，调节时间减小时，为满足这一调节，输入u在短时间内有1个激增然后迅速减小，稳定在某个值上，对应地使滑动变量s趋于零，根据式（11）的计算结果，状态量x（输出y即为第 1个状态x1=ΔNf）有1个短时间的超调。为验证推理，可在matlab中改变η对比仿真结果，如图4所示。实际选择参数η，保证各被控量不超限，应使调节时间尽可能短。

上述过程中的变化以矩阵G值不变为前提。G值的设定用来改变输出的动态响应特性，反映了极点的位置。

图4 改变η时，ΔNf的响应结果对比

2 极限保护控制设计及与稳态控制的综合

2.1 理论分析

滑模控制方法在同时实现发动机的鲁棒性和极限保护方面表现出很强的优越性。基于极限保护控制中普遍采用max-min控制逻辑，滑模控制方法能够克服线性控制器的许多缺陷。max-min/SMC方法的中心思想是针对不同的限制输出和主控制输出，定义不同的滑动变量。限制输出变量所对应的滑动变量与稳态控制器设计类似，定义为限制输出变量与极限值的差值。当某个滑模控制器起作用时，相应的限制输出不会超过其设定的极限值，其他变量也不会超过其限制量。其控制逻辑如图5所示。

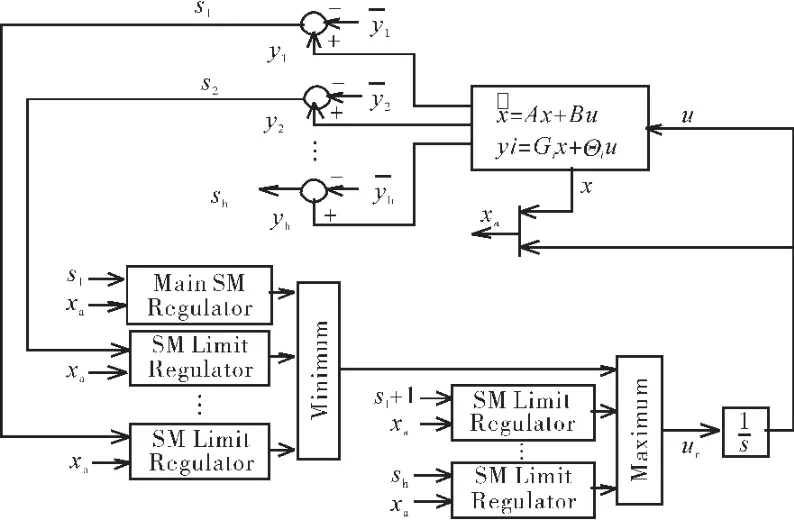
图5 max-min/SMC控制逻辑

与基于线性调节器的最大最小选择逻辑相比，基于滑模控制的最大最小选择逻辑的所有输出原则上都不会超过其限定值，其优势明显。

对于1种新的控制律，最重要的是保证其稳定性[12]。max-min/SMC方法已被证明是渐进稳定的，能保证稳态误差收敛到零。

从图5可得

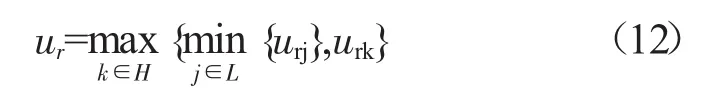
式中：L={1，2，…，l}；urj为与最小选择器相关联的控制器输出；H={l+1，l+2，…，h}；urk为与最大选择器相关联的控制器输出。

图5中各限制保护的滑模控制器设计与稳态滑模控制器设计类似，设发动机模型为

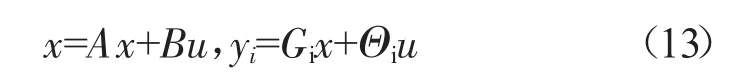
式中：yi为不同极限保护控制量，对应到发动机为涡轮前温度、喘振裕度等。由si=yi-，令=-ηi·sign（si），设ur=，可得

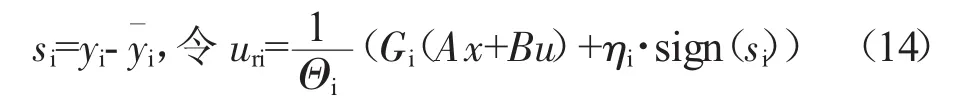
由此可证，最大、最小选择器的类型与输出变量要求的上限或下限以及有关，结论见表1。

表1 max-min/SMC选择逻辑类型的规则

2.2 参数设定对极限保护效果的影响

在矩阵G确定的前提下，即s（0）已知，这时主要影响滑模到达时间的是η。从η的定义式可见，˙=-η· sign（s），是s的微分前的系数，即s的变化速率，可表示为：s=e-η·esign（s）。从图4中可见，η越大，调节时间越短，所带来的超调也越大；η越小，调节时间越长，超调量相应减小。

当控制系统中有多个滑模控制器并利用最大最小选择逻辑来进行协调配合时，若均为最小选择逻辑，当某些SMC的η选择较小时，SMC的值也偏小，其作用体现不明显；若均为最大选择逻辑时，结果相反。通过以下例子（Ps30/Wf最小选择逻辑）求解，如图6所示（设定限制值为0）。从图6（a）中可见，η较大，控制作用较强，Ps30/Wf即使有短时间超限也会被抑制；从图6（b）中可见，η较小，短时间超限被忽略，长期如此会严重影响发动机寿命[13]。与此同时，研究发现，极限保护在争夺控制权限时，η对抖振也有重要影响，如图7所示。因此，合理选择主稳态控制器以及各极限保护控制器中的参数η，能使各控制器均在极限保护中发挥作用，同时最大程度地减少抖动。

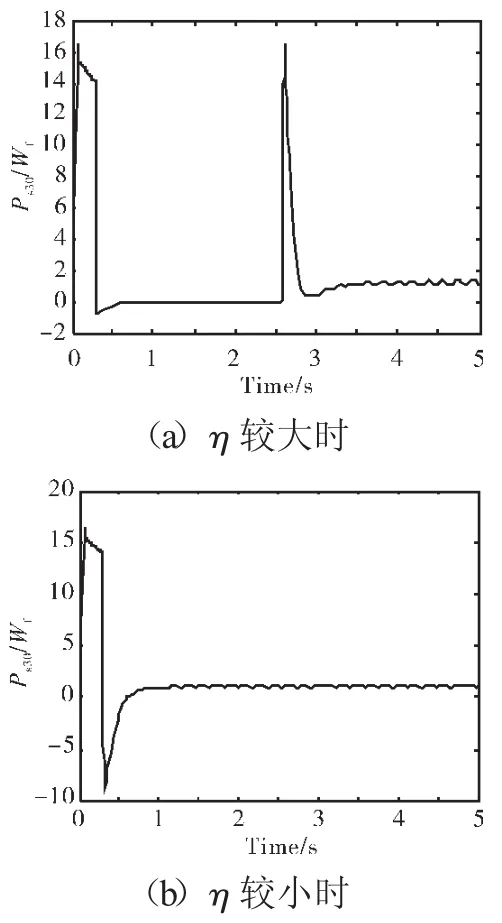
图6 在多SMC控制器切换中Ps30输出响应

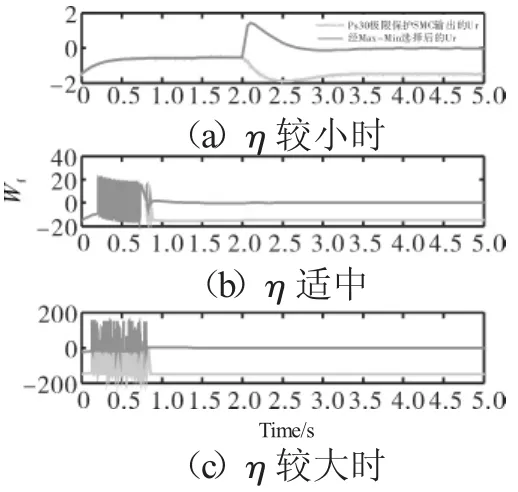
图7 不同η值下FWf比较结果

2.3 仿真实例

仿真中所用发动机线性模型的各系数矩阵根据表1选择规则确定：控制T48不超过上限，其调节器应选择Min逻辑；控制PER不超过上限，同样选择Min逻辑；要求Ps30不超过下限，选择Max逻辑；要求Ps30不超过下限，选择Max逻辑。最终结果如图8所示（图中虚线表示极限限制值）。

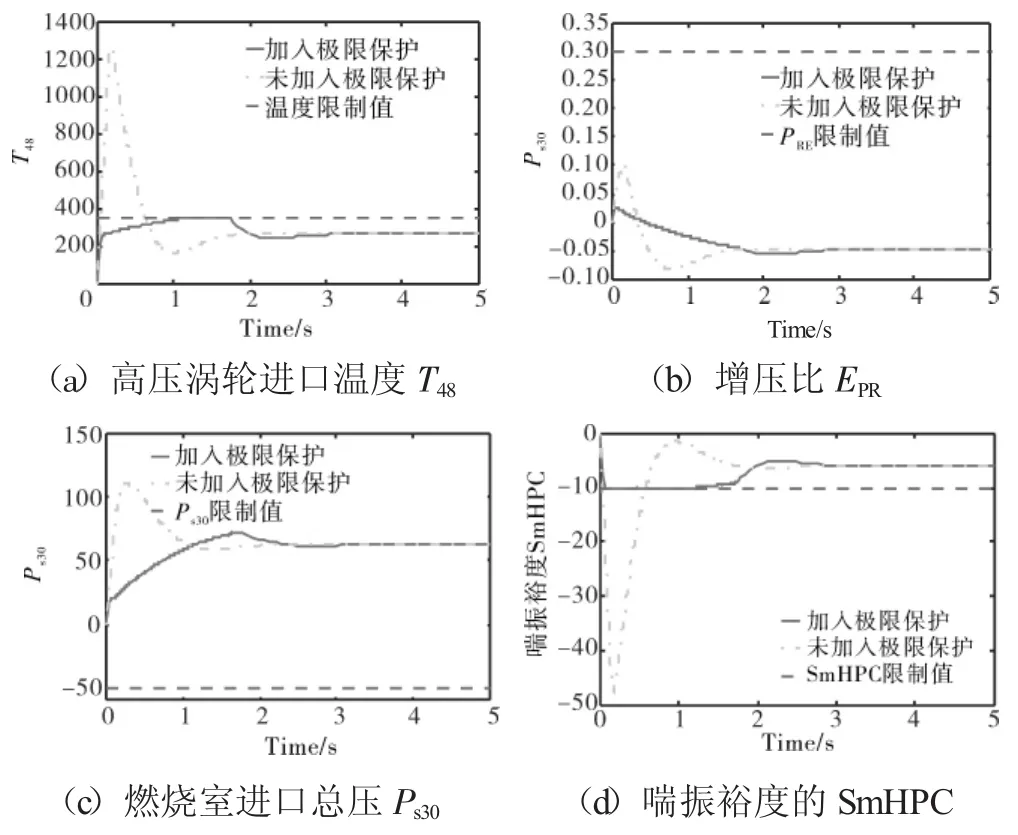
图8 极限保护结果

为与前述稳态控制器实例结合，仍采用Wf为控制量，主被控制量为风扇转子转速偏移量ΔNf，期望值为340，其他限制保护的被控量为T48、PRE、Ps30，仿真结果如图8所示（ΔNf试验结果与图1的类似，但调节时间略有延长，篇幅有限，这里不列图示意）。

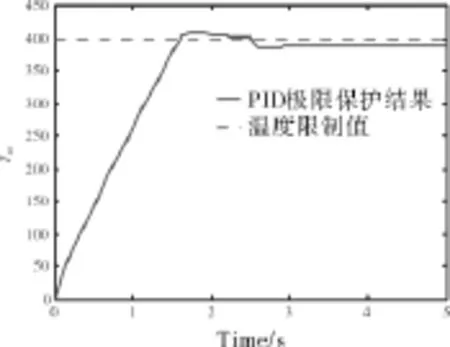
图9 PID控制方法的极限保护效果

从图中可见，只要最后的控制权限落在控制ΔNf的调节器中，那么ΔNf的稳态误差必然为零，因为滑模控制可使滑动变量s趋于零，对应地，即达到风扇转速的期望值。相比于传统线性控制，max-min/SMC控制逻辑在主控制器与极限保护控制器综合作用时，能保证各限制变量不超过限定值，更能发挥发动机潜能。控制的意义在于使发动机工作状态尽可能地靠近其极限，加入极限保护必然会增加调节时间，即不超限是以牺牲一部分性能为代价的，如果某种控制方法能使发动机更加靠近其极限边界，则这种性能损失越小。线性控制虽然也能保证不长时间超限[14]，如图9所示。但也绝不可能使极限保护的量达到界定边界（限于篇幅，不列图示意），在实际应用时，相对于安全边界留有一定裕度；同时，由于PID调节作用较温和，使得最后稳定所需的调节时间较长。滑模控制在这方面表现出明显优势，提升了发动机机动性能。

3 抖振的研究

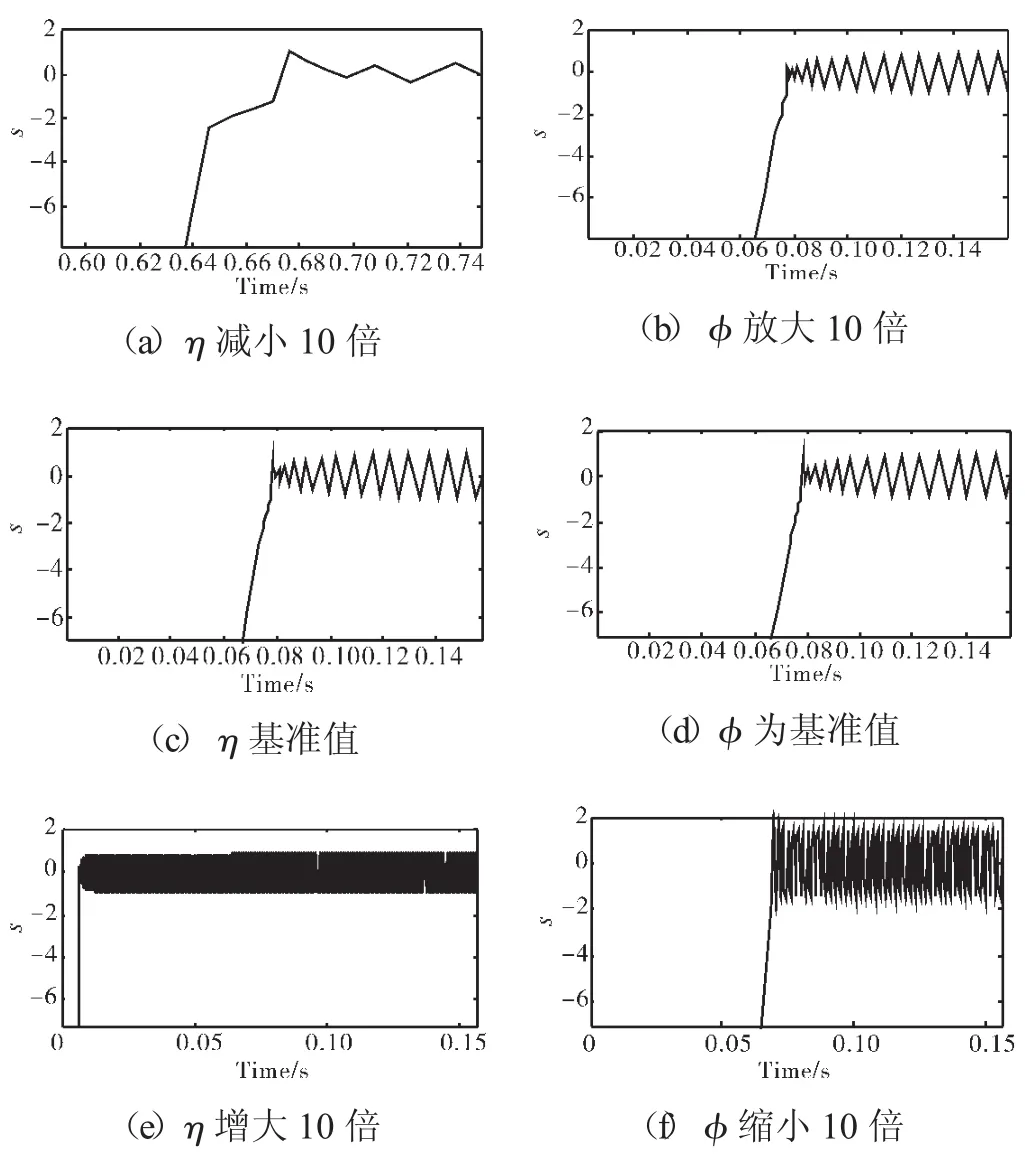
图10 滑模控制抖动放大效果

滑模控制具有强鲁棒性，如果不改变控制器的参数，仅将不同的稳态点模型替换进行仿真，滑动函数最后能稳定在s≠0的某个值上，仿真发现抖动非常大，其鲁棒性越强，模型不准确时最后达到的稳态值越接近期望值。实践中只能对抖动与鲁棒性进行最佳折中。

为改善滑模控制的抖动问题，利用饱和函数替代实现条件中的符号函数，使得处于零值附近的s（x）的不为第2类间断点。同时，在SMC极限保护控制器的设计过程中发现η对抖动也有很大影响。通过分别改变φ和η的值来讨论其对抖动的影响，结果如图10所示。

从图10中可见，η（计算时主要考虑其对滑模到达时间，即调节时间的影响）对抖动的影响要比边界层厚度φ大。在实际应用中，η主要用于计算调节时间。φ的设计目的是尽可能地减弱抖动。当然，在后续研究中可尝试其他较新的消抖方法。

4 硬件在回路实时仿真试验验证

随着计算机技术的不断发展，仿真技术逐步被引入航空发动机控制领域，以其短周期、低成本、低风险的巨大优势成为研制先进水平发动机数字控制系统的重要途径。基于发动机控制系统研制实时性的要求和航空发动机数控系统实时仿真平台[15]，从模型建立开始，经过控制规律分析和仿真、自动代码生成、代码编译链接、下载至实时控制器硬件直至在由被控对象、执行机构、传感器等真实硬件设备所构成的闭环回路中运行控制系统等一系列完整过程，将利用滑模控制方法设计的控制器在硬件在回路平台上进行了仿真验证。

下面以加入极限保护（仅加入T48）的滑模控制器与主控制器（控制风扇转子转速ΔNf）的综合系统的试验为例，将整个过程的试验数据导入Matlab工作空间，如图11所示。

图11 硬件在回路平台与Matlab仿真结果对比

图12 发动机与控制器端数据对比

试验结果与数字平台仿真结果对比如图12所示。由于试验中连续系统离散化，考虑到数据转换、A/D和D/A处理等造成的误差，在试验允许范围内，二者的趋势大致相同。在后期研究中可以采用更高精度的数模转换单元或更改数据传输方式来解决。本文基于Vxworks的仿真系统为硬实时系统，即一旦计算负载超过硬件可承受值，仿真将中断，而多次仿真验证中也无迟滞现象，说明这种基于滑模控制规律的极限保护与稳态控制器相结合，可以在现有硬件平台下实时运行。因此，在如该试验平台的的软、硬件配置下，由滑模控制方法设计的控制器能实时仿真，具有工程价值。

5 结论

（1）基于滑模控制方法的控制器，在极限保护控制中保证了极限保护变量不超限，使得发动机在设置输出变量的限定值时，不必像传统方法那样保守，能更好地发挥发动机的潜能。

（2）滑动系数η和边界层厚度φ均会对滑模控制的抖动产生影响，且前者的影响比后者的大。

（3）硬件在回路平台上的仿真结果表明：在该平台的软、硬件配置下，滑模控制器的实时性能够得到保证。

[1]Shtessel Y B，Shkolnikov I A，Levant A.Guidance and control of missile interceptor using second-order sliding modes[J].IEEE Transactions on Aerospace and Electronic Systems，2009，25（1）：110-123.

[2]Ferrara A，Magnani L.Motion control of rigid robot manipulators via first and second order sliding modes[J].Journal of Intelligent Robot Systems，2007，48（1）：23-36.

[3]王丰尧.滑模变结构控制[M].北京：机械工业出版社，1995：21-51. WANG Fengyao.Sliding mode variable structure control[M].Beijing：China Machine Press，1995：21-51.（in Chinese）

[4]Garg S.Aircraft turbine engine control research at NASA Glenn Research Center[R].NASA-TM-2013-217821.

[5]Richter H，Litt J S.A novel controller for gas turbine engines with aggressive limit management[R].AIAA-2011-5857.

[6]Richter H.Multiple sliding modes with override logic：limit management in aircraft engine controls[J].Journal of Guidance，Control，and Dynamics，2012，35（4）：1132-1142.

[7]Richter H.Advanced control of turbofan engines[M].New York：Springer Science and Business Media，2012：111-139，117-201.

[8]陆军，郭迎清，王磊.航空发动机过渡态最优控制规律设计的新方法[J].航空动力学报，2012，27（8）：239-245. LU Jun，GUO Yingqing，WANG Lei.A new method for designing optimal control law of aeroengine in transient states [J].Journal of Aerospace，2012，27（8）：239-245.（in Chinese）

[9]Csank J，Ryan D M，Jonathan S L，et al.Control design for a generic commercial aircraft engine[R].AIAA-2010-6629.

[10]赵连春，杰克·马丁利.飞机发动机控制——设计、系统分析和健康监视[M].北京：航空工业出版社，2009：78-95. Jaw Link C，Jack M D.Aircraft engine control:design,system analysis and health monitoring[M].Beijing：Aviation Industry Press，2009：78-95.（in Chinese）

[11]刘金锟.滑模变结构控制MATLAB仿真[M].北京：清华大学出版社，2005：1-64. LIU Jinkun.MATLAB simulation for sliding mode control[M].Beijing：Tsinghua University Press，2005：1-64.（in Chinese）

[12]Ryan D M，Csank J.A high-fidelity simulation of a generic commercial aircraft engine and controller[R].AIAA-2010-6630.

[13]陈小磊，郭迎清，张书刚.航空发动机寿命延长控制综述[J].航空发动机，2013，39（1）：17-22. CHEN Xiaolei，GUO Yinging，ZHANG Shugang.Summary of life extending control for an aeroengine[J].Aeroengine，2013，39（1）：17-22.（in Chinese）

[14]刘金锟.先进PID控制及其MATLAB仿真[M].北京：电子工业出版社，2003：1-48. LIU Jinkun.Advanced PID control and MATLAB simulation[M].Beijing：Publishing House of Electronics Industry，2005：1-48.（in Chinese）

[15]陆军.航空发动机数控系统实时仿真平台研制 [D].西安：西北工业大学，2008. LU Jun.Developing of aeroengine numerical control system real-time simulation platform[D].Xi'an：Northwestern Polytechnical University，2008.（in Chinese）

[16]杜宪，郭迎清.民用涡扇发动机预测控制器设计[J].航空发动机，2013，39（3）：27-30. DU Xian，GUO Yingqing.Design of model predictive controller for commercial turbofan engine[J].Aeroengine，2013，39（3）：27-30.（in Chinese）

(编辑：赵明菁)

Improved Design for Aeroengine Control System Based on Sliding Mode Control Method

XU Qing-shi，GUO Ying-qing
（School of Power and Energy，Northwestern Polytechnical University，Xi'an 710072，China）

In order to improve inherent vice in limit protection which were designed by traditional method of aeroengine control system based on linear regulators（PID）,a nonlinear control method on Sliding Mode Control（SMC）replaced the usual PID regulators was proposed.The steady-state controller was combined with limit regulators based on the traditional max-min selector system.Compared with controller by PID,the controller by SMC can ensure that engine have a better performance with the prescribed limits.Effects of parameters such as the boundary layer thickness on sliding mode were discussed.SMC system was applied on a hardware-in-the-loop real-time simulation platform.Results show that the method can meet the real-time requirements.

sliding mode control(SMC)；PID；min-max logic arrangement；hardware-in-the-loop real-time simulation；aeroengine

V 233.7

A

10.13477/j.cnki.aeroengine.2015.06.007

2015-05-14

徐清诗（1993），女，在读硕士研究生，研究方向为航空发动机控制；E-mail：xqs@mail.nwpu.edu.cn。

徐清诗，郭迎清.基于滑模控制改进发动机控制系统设计，2015，41（6）：33-38.XUQingshi，GUOYingqing.Improveddesignforaeroenginecontrol systembasedonslidingmodecontrolmethod[J].Aeroengine，2015，41（6）：33-38.