基于张量多线性PCA的多变量时间序列模式匹配
2015-01-03董红玉陈晓云潘江山
董红玉,陈晓云,潘江山
(福州大学数学与计算机科学学院,福建福州 350116)
多变量时间序列(multivariate time series,MTS)是指多个变量依照时间先后顺序得到的一系列观察值的集合,常用一个n×m的矩阵表示,其中n代表序列长度,m代表变量个数[1,2].MTS数据广泛存在于视频监控、金融和医疗等各种应用领域,故对其挖掘具有广阔的应用前景[3].依照挖掘目标的不同,MTS挖掘包括模式匹配[3-4]、主题发现[4]、异常检测[5]、监督和无监督的分类[1]等.
MTS模式匹配是指将数据集的一个MTS样本的模式表示作为输入,计算与数据集中的其余模式相似度的过程[4].MTS的模式表示和相似性度量是MTS模式匹配的两大关键步骤.
1 相关研究
现有MTS模式匹配方法可分为参数法和非参数法.参数法是指对MTS建立模型,用模型参数度量其相似度,如文[6]对MTS建立向量自回归模型,计算各模型参数间的相似度.而难以选择恰当的模型是此类方法的不足.
非参数法则先提取MTS的模式表示,之后根据选取的相似性度量计算模式之间的匹配程度.文[7]提出基于点分布特征的模式匹配方法,提取MTS的局部极值点作为其模式,并由局部极值点的统计分布特征组成特征向量,之后计算特征向量的欧氏距离,此方法适用于小规模的MTS数据集,对大规模数据集,其匹配效果较差.文[8]采用多维分段线性拟合方法提取拟合线段的倾斜角、时间跨度与序列长度的比值作为多变量时间序列的模式表示,并用DTW距离做为模式相似性度量.其不足之处在于模式参数由经验给定,缺乏自适应性且计算DTW距离的时间开销较大.文[9]提出基于单线性PCA的模式匹配算法,利用PCA对MTS的序列长度进行降维,并提取降维后的前z个主成分作为原MTS的模式表示,而模式相似性度量则采用如下的夹角余弦平方公式:

其中:X和Y是两个MTS样本,θij表示X的第i个主成分与Y的第j个主成分的夹角,主成分的个数z由其贡献率决定.该方法的不足之处在于利用PCA降维时仅考虑序列长度降维而忽略了多变量间的相关性,且夹角余弦平方不满足三角不等式;文[10]将MTS的协方差矩阵的右奇异分解矩阵作为其模式表示,并利用奇异值对右奇异矩阵加权,以加权的右奇异矩阵列向量间的内积绝对值作为模式相似性度量,其公式如下:


2 基于张量多线性主成分的MTS模式匹配
文[9]采用的单线性PCA方法和文[10]采用的奇异值分解方法仅对MTS序列长度进行降维,MTS的多个变量间也可能存在冗余.文本将多变量时间序列看成一个二阶张量(矩阵),通过对MTS进行多线性PCA变换,变换后得到的序列模式不仅序列长度降低,变量个数也可减少,即对MTS进行双向降维,降维后的MTS仍以矩阵的形式表示.为了度量矩阵形式表示的模式间相似度,本文采用Frobenius范数作为MTS模式的相似性度量.下面给出方法的相关定义与原理.
多变量时间序列的数学表达.多变量时间序列(multivariate time series,MTS)是指由多个变量按照时间顺序所记录的一系列观察值的集合,记为Xi(t),(i=1,2,…,m;t=1,2,…,n).其中i表示变量个数(m≥2),t表示序列长度.它可以用一个n×m的矩阵表示如下:其中:xit表示第i个变量在t时刻的观察值.
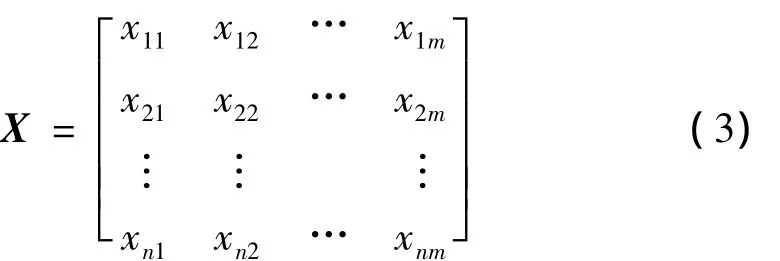
图1为一个来自JV数据集的MTS样本,其变量个数为12,序列长度为21.
张量[11]是一个多维数组.用数学观点来说,一个N阶张量是N向量空间中一个实多重线性函数.张量Α∈RI1×I2×…×IN的阶为 N.
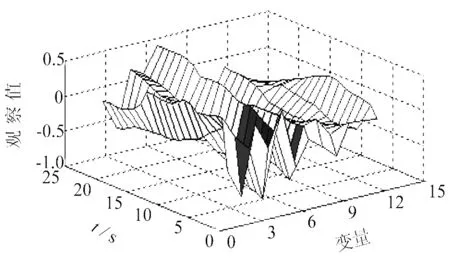
图1 MTS的3D图像Fig.1 Tree- dimensional graphics of MTS
2.1 基于张量多线性PCA的MTS模式表示
MTS样本X∈Rn×m是张量空间Rn⊗Rm的一个二阶张量.设(u1,u2,…,un),(v1,v2,…,vm)分别是空间Rn,Rm的标准正交集,则MTS样本X可唯一写成

其中:{uivTj}构成张量空间Rn⊗Rm的基.定义二阶张量U=(u1,u2,…,ul)∈Rn×l和V=(v1,v2,…,vs)∈Rm×s(l<n,s<m).假设μ,ν分别是空间中由基向量{ui}li=1,{vj}sj=1张成的子空间,则二阶张量X∈Rn×m在低维子空间μ⊗ν上的重构可写为

张量多线性PCA的目标[12]是寻找少数几个最大特征值对应特征向量所张成的张量子空间,使重构误差最小.对于MTS数据集D={X1,X2,…,Xd},其张量多线性PCA重构的目标函数为[13]

其中:Yi是MTS样本Xi在张量子空间μ⊗ν上的重构,为所有MTS样本在子空间μ⊗ν的重构均值

由矩阵Frobenius范数的定义 Q2=tr(QQT)=tr(QTQ),可推出[12]

其中:

则最佳二阶投影张量U,V分别是DV,DU的最大特征值对应特征向量所组成的二阶张量.不失一般性,取 U,V 为正交矩阵,即 UUT=I,VVT=I,故[12]

从而最佳二阶投影张量U,V分别是D'V,D'U的最大特征值对应特征向量所组成的二阶张量.
由式(5)可知,MTS样本在低维子空间的重构由二阶投影张量U,V确定.因此,二阶投影张量U,V的维数选择至关重要.分别求得D'V,D'U的特征值和特征向量,本文选择特征值贡献率占所有特征值98%的特征值所对应的特征向量构成U,V的列向量.
2.2 MTS的相似性度量
提取MTS的低维重构作为其模式表示之后,需要一个恰当的相似性度量去描述两两模式间的相似度以完成模式匹配.对于两个MTS样本X1=(x1ij)n×m和 X2=(x2ij)n×m,经多线性PCA重构后的模式表示为Y1=(y1ij)l×s和 Y2=(y2ij)l×s(l<n,s<m),样本X1和X2的相似性度量定义如下:

其中: ·F为Frobenius范数.由于Frobenius范数满足三角不等式,故SDLPC也满足三角不等式.
3 实验结果与分析
3.1 实验数据
本文选取四组 MTS 数据集进行实验,分别为 Wafer[9-10]、ECG[9-10]、JV[14]和 LP1[15],表 1 概要描述了这四组实验数据.

表1 实验数据概述Tab.1 The Summary of datasets used in experiments
Wafer是硅晶体生产过程中用6个真空传感器所记录的半导体微电子序列,每个硅晶体用一个MTS刻画,分为normal和abnormal两类,327个样本中200个属于normal类,127个属于abnormal类;ECG是用2个电极测得的一组心跳数据,包括normal和abnormal两类,200个样本中133个属于normal类,67个属于abnormal类;JV是记录9个测试者的12个同态谱数据描述的日文元音发音过程,每次发音作为一个MTS;LP1是Robot Execution Failure数据集的一个子数据集,它通过6个传感器对Robot进行异常监控.
3.2 实验方法
采用k-近邻法进行实验.假定数据集包含d个样本,任意选取一个样本X作为输入,对数据集中所有样本进行重构,得到其模式表示,采用k-近邻法寻找与输入样本X最相似的k个样本,本文分别取k=1,5,10,最后统计这k个样本中与输入样本X具有相同类标签的样本个数n,由式(15)计算准确率c

依次将其它样本作为输入,重复以上过程,得到d个准确率.根据本文k的取值,准确率c的取值应为{0,0.1,0.2,…,1},记为 ci(i=1,2,…,11),计算准确率的比率 p如下:

进一步由式(17)计算整个数据集的准确率期望值

准确率期望值越高,表明该模式匹配方法越好.此外,由于在进行样本重构时,张量多线性PCA要求样本序列长度一致.因此,对于不等长数据集,通过截取使所有样本序列长度与数据集中最短的序列长度一致.
3.3 三种模式匹配方法准确率比较
实验主要比较三种多变量时间序列模式匹配方法的准确率:本文方法(张量多线性PCA+Frobenius范数)、文[9]方法(单线性PCA+夹角余弦平方和)及文[10]方法(奇异值分解+加权内积绝对值)的模式匹配准确率.分别采用这三种模式匹配方法在Wafer、ECG、LP1和JV四组数据集上测试,统计近邻数k=1,5,10时三种方法各准确率上的匹配样本数.下文给出ECG数据集的实验结果,如表2所示,其余数据集的实验结果详见表3.
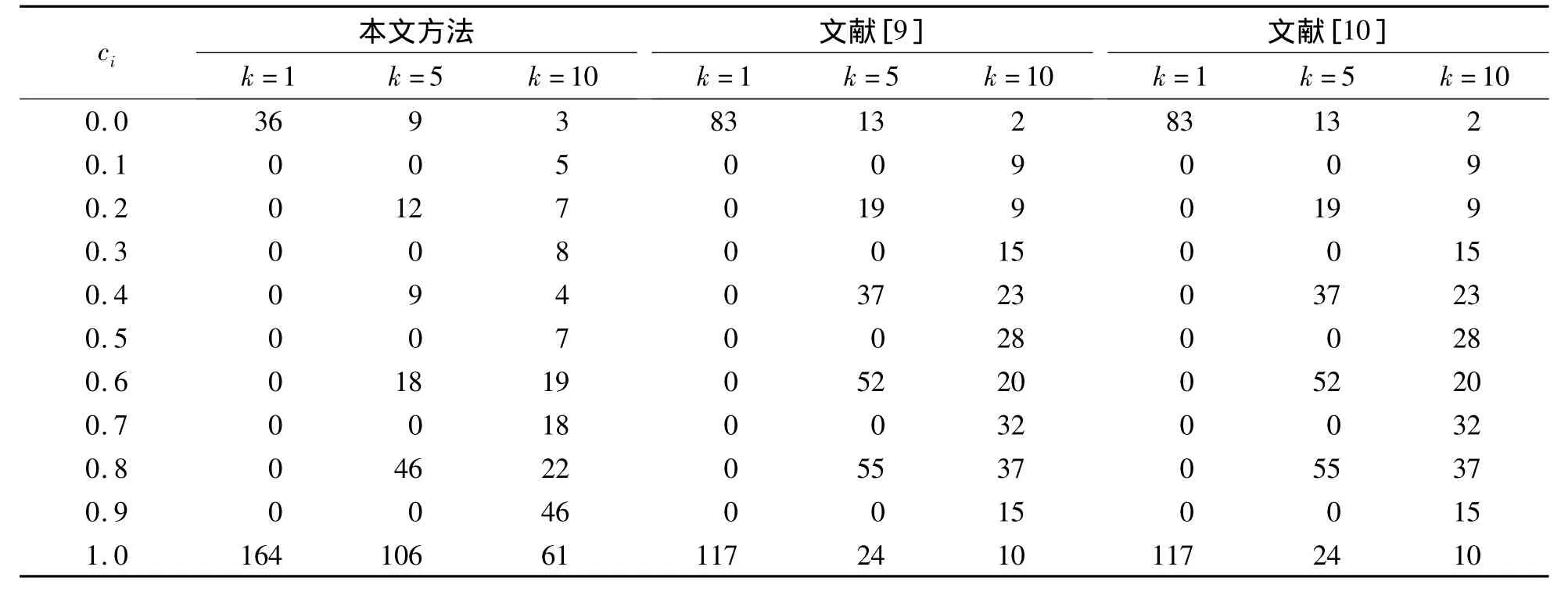
表2 三种模式匹配方法在ECG数据集上各准确率的匹配样本数Tab.2 Matching number of accuracy of 3 pattern matching methods on ECG dataset
由表2可知,对于ECG数据集,当准确率较小时,本文方法的匹配个数远小于文[9-10]的方法;当准确率较高时,本文方法的匹配个数远大于文[9-10]方法.特别指出的是,当准确率为1时,本文方法在ECG数据集上三种近邻对应的匹配个数比文[9-10]方法多60个左右.四组数据集的实验结果表明本文方法对数据集的序列长度不限制,且匹配效果远好于文[9-10]方法.进一步由式(16)~(17)计算得到四个数据集各自的准确率期望值,结果见表3.

表3 三种模式匹配算法在四组数据集上的准确率期望值Tab.3 Accuracy expectations of 3 pattern matching methods on 4 datasets
观察表3可知,对四组数据集而言,在三种不同的近邻数模式匹配情况下,本文方法的匹配期望准确率都比文[9-10]方法高.特别指出:对于ECG数据集,三种模式匹配状态下,本文方法的准确率期望值比文[9-10]方法提高了约20%.对于LP1数据集,本文方法的准确率期望值约为77%,而文[9-10]的准确率期望值仅约为44%,这说明文[9-10]方法不适于序列长度较短的数据集,而本文方法则没有这方面的局限.
3.4 三种模式匹配方法时间开销比较
在四组数据集分别测试采用本文方法、文[9-10]方法的时间开销,实验结果如图2所示.可以直观地看出,在四组数据集上,本文方法的时间开销都远少于文[9-10]方法.

图2 三种模式匹配算法在四组数据集上的时间开销比较Fig.2 Computational time comparision of 3 pattern matching methods on 4 datasets
4 结论
提出基于张量多线性PCA的模式匹配方法.该方法使用张量多线性PCA对多变量时间序列进行低维重构,得到序列长度及变量个数均被减少的模式表示,并采用Frobenius范数度量矩阵形式表示的模式的相似度.在四组真实MTS数据集上实验结果表明该方法比现有多变量时间序列模式匹配方法的匹配准确率更高,匹配时间更短且适用不同序列长度的数据集.
[1]Jeong Y S,Jeong M K,Omitaomu O A.Weighted dynamic time warping for time series classification[J].Pattern Recognition,2011,44(9):2 231-2 240.
[2]Pham T D.Possibilistic nonlinear dynamical analysis for pattern recognition[J].Pattern Recognition,2013,46(3):808 -816.
[3]丁永伟,杨小虎,陈根才,等.基于弧度距离的时间序列相似度量[J].电子与信息学报,2011,33(1):122-128.
[4]Frank J,Mannor S,Pineau J,et al.Time series analysis using geometric template matching[J].IEEE Transactions on Pattern Ananlysis and Machine Intelligence,2013,35(3):740-754.
[5]刘博宁,张建业,张鹏,等.基于曲率距离的时间序列相似性搜索方法[J].电子与信息学报,2012,34(9):2200-2 207.
[6]Raquel P,Francisco M,Gabriel H.Multivariate time series modeling and classification via hierarchical VAR mixtures[J].Computational Statistics& Data Analysis,2006,51(3):1 445-1 462.
[7]管河山,姜青山,王声瑞.基于点分布特征的多元时间序列模式匹配方法[J].软件学报,2009,20(1):67-79.
[8]李正欣,张凤鸣,李克武.基于DTW的多元时间序列模式匹配方法[J].模式识别与人工智能,2011,24(3):425-430
[9]Singhal A,Seborg D E.Pattern matching in historical batch data using PCA[J].IEEE Control Systems Magazine,2002,22(5):53-63.
[10]Yang Kiyong,Shahabi C.A PCA -based similarity measure for multivariate time series[C]//Proceeding of the Second ACM International Workshop on Multimedia Databases.Washington:ACM Press,2004:65 -74.
[11]王甦菁.流形上的张量子空间人脸识别算法的研究[D].长春:吉林大学,2012.
[12]Lu Haiping,Plataniotis K N,Venetsanopoulos A N.MPCA:Multilinear principal component analysis of tensor objects[J].IEEE Transactions on Neural Networks,2008,19(1):18 -39.
[13]Lee K,Park H.Probabilistic learning of similarity measures for tensor PCA[J].Pattern Recognition Letters,2012,33(10):1 364-1 372.
[14]Mineichi K,Jun T,Masaru S.Japanese vowels[EB/OL].2009.http://kdd.ics.uci.edu/databases/Japanese Vowels/Japanese Vowels.html.
[15]Lopes L S,Camarinha - Matos L M.Robot execution failures[EB/OL].2009.http://kdd.ics.uci.edu/databases/robotfailure/robotfailure.html.
