基于可变带宽多速率处理算法的设计与实现

冯佳梅，邹 刚，朱 南，丁 伟，姜 彬，赵文多

（成都国恒空间技术工程有限公司，成都 610041）

基于可变带宽多速率处理算法的设计与实现

冯佳梅，邹 刚，朱 南，丁 伟，姜 彬，赵文多

（成都国恒空间技术工程有限公司，成都 610041）

本文立足于实际信号处理应用中对多速率处理技术的需求，介绍了一种可变带宽的多速率处理算法，该算法采用成型滤波器、级联半带滤波器及分数倍插值滤波器相结合的方式，实现可变带宽的多速率处理。文中还通过Simulink仿真及FPGA设计实现，验证了该算法的性能及可实现性。

可变带宽；多速率；滤波器；FPGA

1 引言

软件无线电技术一直是数字信号处理领域的研究热点，它的基本思想是让数字处理单元尽可能靠近天线，减少模拟域信号处理面积，从而在相同的硬件设计平台上，实现多频段、多用户、多模式的数据处理。随着无线通信技术的快速发展，多种协议体制的不断提出，提高信号带宽利用率，能够兼容不同速率、不同带宽的通用软件无线电设计平台就显得尤为迫切。在软件无线电系统中，若要射频端兼容不同速率的信号，要求在发送端不同输入符号率的信号经过多速率处理后输出信号的采样率与本地数模转换器采样率一致。

目前，带宽可变的多速率处理算法多采用多通道的方式实现，针对不同符号率的信号，进行通道选择的方式实现目标采样率输出。然而该处理方式存在资源占用率高、灵活性与可扩展性差等缺点。针对以上不足，本文提出一种带宽可变多速率处理算法，该算法设计灵活，可适应任意速率要求，给出了发送端多速率处理算法原理及设计结构，且进行了Simulink仿真和FPGA设计实现。

2 可变带宽多速率处理算法及结构

信号发送端多速率处理也即通过插值滤波器的方式提高信号的采样率至目标采样率。由于输入信号的带宽为任意可变，且采样率为一固定值，当输入信号符号率与目标采样率不为整数倍关系时，需要使用分数倍插值算法实现分数倍内插。因此，本文采用整数倍内插与分数倍内插相结合的方式实现可变带宽的多速率处理。按符号率输入的信号序列首先经过固定倍数的插值成型，送入整数倍内插单元实现2的整数次幂的插值处理，整数倍内插后的采样率与目标采样率的插值倍数不超过2倍。然后经过分数倍内插，实现1～2倍的插值，使得分数倍内插的输出采样率即为目标采样率。最后通过DAC单元对信号进行固定采样率的数模转换变为模拟信号。发送端多速率处理框图如图1所示。

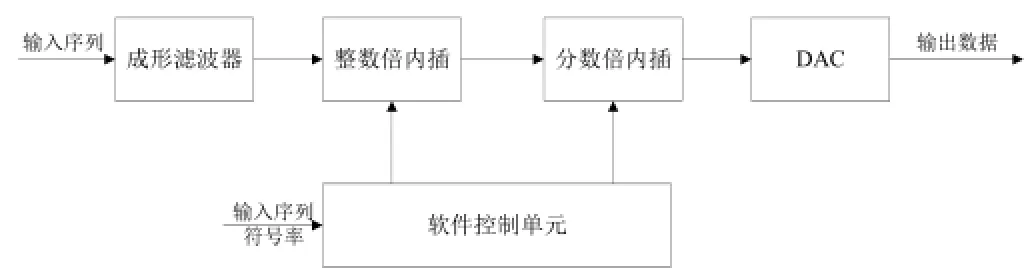
图1 发送端多速率处理结构框图

软件控制单元用于根据输入序列的符号率计算整数倍内插和分数内插的参数，在参数计算过程中存在除法等运算，因而这里采用软件计算的方式，再通过硬件设计接口传输给多速率处理单元。

成型滤波器单元，完成固定倍数的上采样滤波，信号频谱成型，这里的滤波器可选用根升余弦滤波器或其他成型滤波器。成型滤波器的插值倍数固定为M倍内插，通过滤波器归一化设计，输入采样率与输出采样率恒定为M倍的关系，因而滤波器参数不会随着输入符号率的变化而变化。

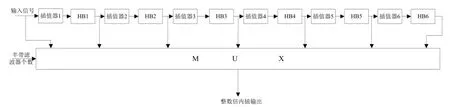
图2 整数倍内插滤波器级联方式

整数倍内插单元，输入序列经过成型滤波器之后送入整数倍内插单元，该单元实现了数据的整数倍插值处理，通过多级滤波器级联的方式能够实现较大倍数的整数倍内插，优先选择计算量为普通FIR滤波器计算量一半，且相比于CIC滤波器增益为0的半带滤波器作为基础滤波器单元，每级半带滤波器实现2的整数次幂内插。通过多级级联的半带滤波器即可实现2的整数次幂的插值处理。以六级半带滤波器为例，各级半带滤波器的级联方式如图2所示。

整数倍内插单元主要包含两个模块：半带滤波器模块和Mux选择器模块。经过成型滤波后的输出数据作为整数倍内插单元的输入信号，且第1级半带滤波器的输入直接是整数倍内插单元输入信号，第1级半带滤波器的输出作为第2级半带滤波器的输入，以此类推，最终将信号送入第n个半带滤波器。同时每个半带滤波器的输出波形均送入Mux选择器，选择器根据软件控制单元提供的半带滤波器个数值选择哪一路半带滤波器的输出数据作为最终整数倍插值单元的输出信号。如半带滤波器个数为3时，需要三个半带滤波器参与滤波，因而Mux选择器选择第三个半带滤波器的输出作为整数倍插值单元的输出信号。

分数倍内插单元接收经过整数倍插值后的输出数据，并进行1～2倍的分数倍插值，使分数倍插值滤波器的输出采样率与目标采样率一致。分数倍内插有多种插值方式，这里选用多项式插值的方式实现。分数倍插值模块可通过多项式插值处理进行设计实现，多项式插值的公式为

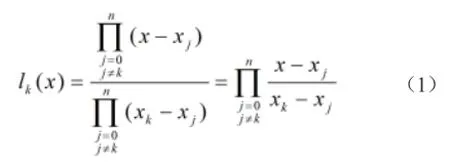
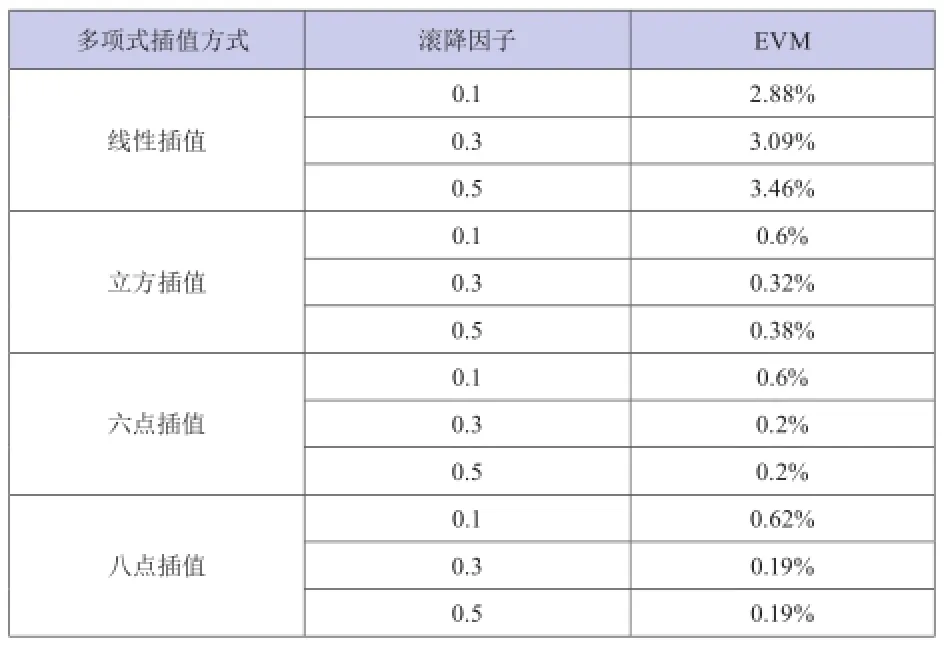
表1 多项式插值EVM分析

线性插值计算出的理论点与插值结果的误差较大，而当大于8个插值点时，受插值结果“龙格”现象的影响，插值性能反而不好。从性能、硬件设计复杂程度及资源利用方面考虑，选择立方插值的方法实现分数倍的插值处理。

DAC单元接收经分数倍插值后的数据，并以固定采样率实现数据从数字域到模拟域的转换，正是由于该模块在任意符号率下均工作在相同的采样率，使得后续的模拟滤波器的带宽保持不变，减小了模拟器件信号处理的压力。

3 参数设计

设目标采样率为fs_u，输入序列符号率为fsymbol_u，多速率各级滤波器设计参数之间的关系为

式中，M为成型滤波器插值倍数；HB_step_u为当前符号率下需要的半带滤波器个数；uk_u为当前符号率下的分数倍插值倍数。首先根据系统需要处理的最小符号率与目标采样率的关系，计算出最多需要的半带滤波器个数；再由当前序列符号率与目标采样率的关系，确定当前符号率下需要的半带滤波器个数HB_step_u和分数倍插值倍数uk_u。其中，对HB_step_u计算采用2的HB_step_u次幂的方式最小逼近目标采样率与当前符号率的比值，如目标采样率与当前符号率的比值为7.5（去掉成型滤波器固定插值倍数后），能够最小逼近的整数倍插值倍数为2的2次幂，因而HB_step_u的值即为2。分数倍插值倍数uk_u为目标采样率与内插后采样率的比值，因为整数倍插值滤波器单元是以2的倍数进行内插，因而分数倍插值倍数uk_u则是0.5～1之间的一个任意值，以前例为例，比值为7.5的插值倍数经过4倍内插后的目标采样率与整数倍内插后的采样率比值为0.5333，因而分数倍插值倍数uk_u的值为0.5333。

4 仿真与实现

设发射机端原始信号为带宽125kHz～8MHz任意可变的QPSK调制信号，初始信号采样率为带宽的4倍。经过多速率插值处理，使得输出信号始终保持64MHz的采样率。搭建的任意数倍上采样率多速率处理模型如图3所示。

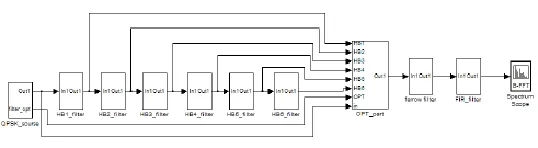
图 3 任意数倍采样率变换Simulink整体仿真框图

当输入信号带宽为1.01MHz时，需要进行63.36633663倍插值，经过4倍的成型滤波器之后，需要3个HB滤波实现，且小数倍插值倍数为0.505。信号经过各级插值滤波后的信号频谱如图4、图5所示。

插值后信号频谱会压缩，插值的镜像信号会被压缩到有效带宽内，而HB滤波器的阻带响应不能将镜像信号抑制至低于噪底，经过插值后会残留一部分的镜像分量。然而镜像分量通过HB滤波器阻带的抑制，幅度在-60dB以下，因而不会对信号有太大影响。

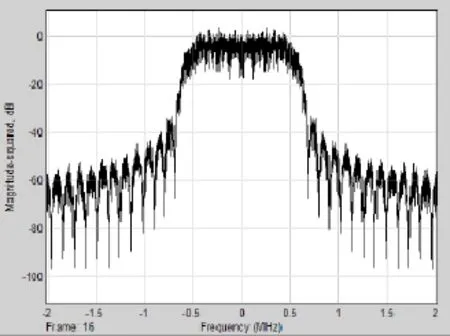
图4 原始信号频谱

图5 多速率处理后的频谱

FPGA以其并行处理方式、高的工作时钟及丰富的逻辑资源，被广泛用于数字信号处理前端。本次设计验证采用XILINX公司Artix7系列中的XC7A200T进行设计实现。编写FPGA硬件设计程序，发送端多速率的整体实现架构如图6所示。

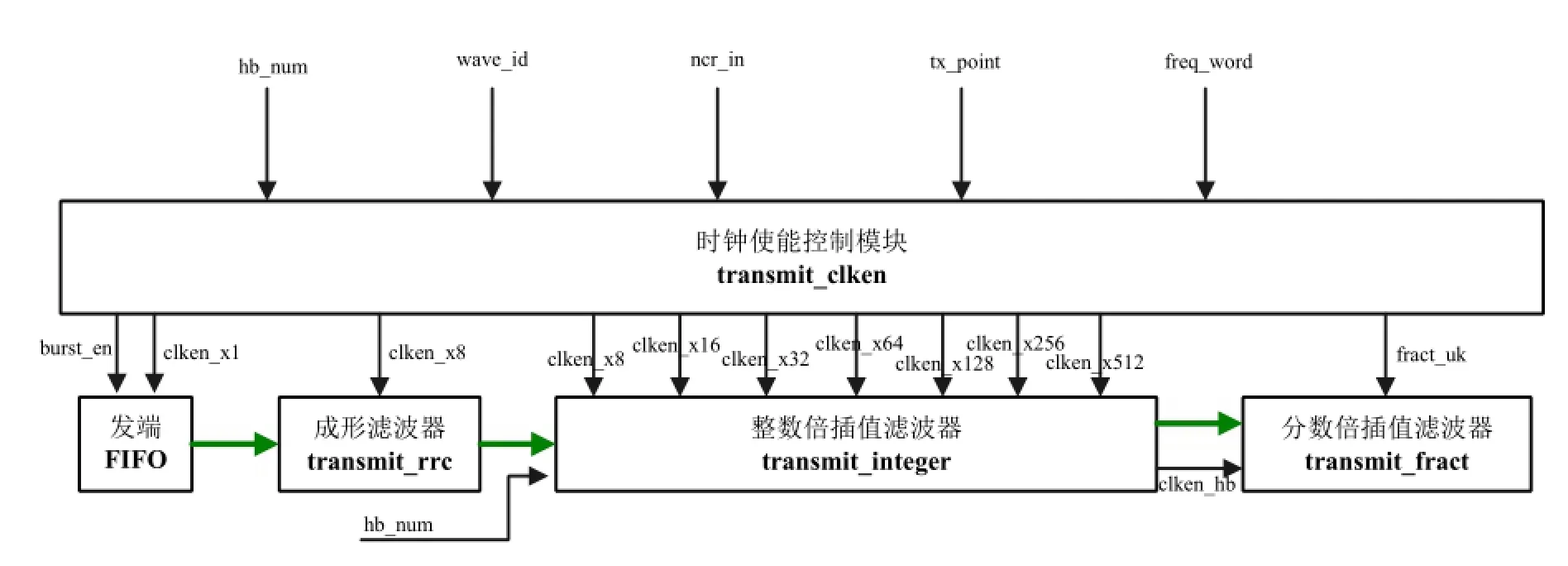
图 6 发送端多速率整体实现架构

其中，时钟使能控制模块用于生成FPGA内部各个设计模块的时钟使能及小数倍插值参数。发端FIFO用于生成不同符号率的信号，为成型滤波器单元提供源文件，成型滤波器单元则用于进行8倍的插值成型，再是整数倍插值滤波器实现整数倍内插，分数倍插值滤波器实现分数倍内插处理。得出经过该发送端多速率处理系统，并在接收端画出了QPSK信号中不同符号率下的星座图如图7所示。

图7中（a）显示了符号率为4MHz时，接收端接收信号的星座图；（b）显示了符号率为3MHz时信号的星座图；（c）显示可符号率为125kHz时信号的星座图，且它们的最终输出采样率均为64MHz，从图中可以看出，通过多速率处理后，由于不同输入符号率下使用的半带滤波器个数不同，因而，随着符号率的减小，星座图的发散度略微有些增大，但均能够很明显地判别出信号所处的相位信息符合设计要求。

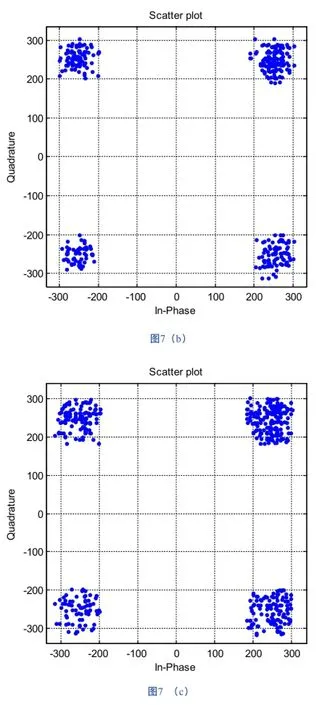
图7 输出信号星座图

5 结束语

本文提出了一种可适用于可变带宽的多速率处理结构，并进行了设计实现。与其他多速率设计结构相比较，本算法利用软件单元对系统的参数进行设计，减少了系统的设计复杂程度，通过动态选择半带滤波器的级数及分数倍插值倍数，实现任意倍数的多速率处理，结构灵活且易于实现。仿真及FPGA设计实现验证了算法的性能及可实现性。

[1] 姜宇柏，游思晴．软件无线电原理与工程应用[M]．北京：机械工业出版社，2007.1-5

[2] Joe Mitola. The Software Radio Architecture[J].IEEE Communications Magazine,1995,12(4):15-23

[3] 董骞．基于软件无线电的SAR数字接收机研究[D]．北京：中国科学院研究生院，2007.12-30

[4] （美）Jeffrey H.Reed 编．陈强译．软件无线电-无线电工程的现代方法[M]．北京：人民邮电出版社，2002.40-62

[5] Wajih A, Abu-Al-Saud, Gordon L.Stuber. Efficient Sample Rate Conversion for Software Radio Systems[J]．IEEE Communication Magazine,2006,54(3):1163-1170

[6] Hentschel T，Fettweis G．Sample rate conversion for software radio[J]．IEEE Communication Magazine,2000,38(8):142-150

[7] Zhenning Tao，Lei Li，Ling Liu．Improvements to Digital Carrier Phase Recovery Algorithm for High-Performance Optical Coherent Receivers[J].IEEE Journal of Selected Topics in Quantum electroni cs,2010,16(5):1201-1209

[8] Ascheid G，OerderM，Stahl J，Meyr H．An All Digital Receiver Architecture for Bandwidth Efficient Transmission at High Data Rates[J] ．IEEE Transactions on Communication,1989,10(3):804-813

[9] Floyd M Gardner. A BPSK/QPSK Timing Detector for Sampled Receivers[J]. IEEE Transactions on Communications, 1986,34(9):423-429

[10] 仇佩亮，陈惠芳等．数字通信基础[M]．北京：电子工业出版社，2007.323-356

[11] Mauro Cimino, Prabhakar Pagilla. Design of Linear Time-Invariant for Multirate Systems[J]. IEEE Conference on Decision and Control, 2009,67(3):2258-2236

[12] 王桂宝，蒋小杰，林吉平，王兰美．多速率转换信号频谱研究[J]．电子科技，2011，24(8):73-75

[13] Alanv oppenheim，Alans willsky, Withs Hamidnawab. 刘树棠译．信号与系统[M]．西安：西安交通大学出版社，1997:254-557

Based on Variable Baseband Multi-rate Algorithm Design and Implementation

Feng jiamei, Zou Gang, Zhu Nan, Ding Wei，Jiang Bin，Zhao Wenduo
(Chengdu GuoHeng Space Technology Engineering Co.,ltd., Chengdu,610041)

On the basis of the requirement about multi-rate processing technology in practice signal processing, this paper introduced a variable baseband multi-rate algorithm which is composed of forming filter, cascaded half-band filter and fraction interpolation filter, used to implement variable baseband multi-rate processing. Gate through Simulink simulation and FPGA implementation, verified this algorithm’s performance and realizability.

Variable baseband; Multi-rate; Filter; FPGA

10.3969/J.ISSN.1672-7274.2015.08.006

TN92文献标示码：A

1672-7274（2015）08-0021-05