整体入手 巧妙解题

浙江 陶云娥

有些数学问题，从局部入手难以解答，如果能运用整体思想去分析，则常常能出奇制胜。

【例1】如图1，淘淘从家出发到学校有三条路可走，那么走哪一条路最近呢？

【分析与解】这道题真奇怪，一个数据都没有告诉我们。怎么算呢？别急，就从整体入手分析解答。设三个小半圆的直径分别为，那么第③条路的长度是第②条路的长度是，第①条路的长度是。所以，三条路一样长。

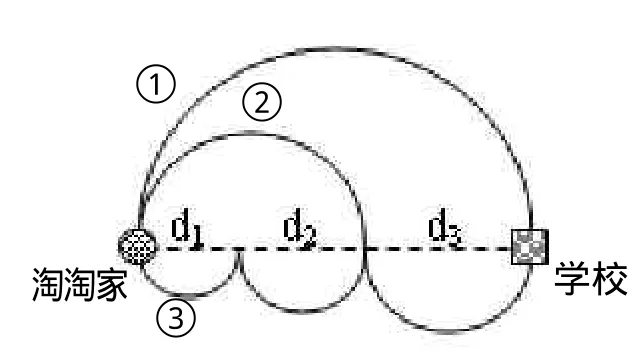
图1

【例2】如图2，已知阴影部分的面积为45cm2，求圆环的面积。

【分析与解】求圆环的面积，通常先要找到大、小两圆的半径，但本题是行不通的。怎么办呢？也从整体入手，根据圆环的面积公式S=(R2－r2)，先算出R2－r2的差，再求解。

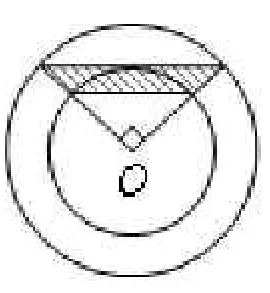
图2

【例3】如图3，一个梯形的四个顶点恰好在四个半径都是1cm的圆的圆心上，求涂色部分的总面积。

【分析与解】本题不要考虑每个扇形的面积各是多少，而要从整体入手，先想弧是虚线的4个空白扇形的总面积有多大。

将梯形分成两个三角形，可以得出梯形的四个内角的和是180°×2=360°。也就是上图中 4个半径相等的空白扇形，圆心角的和是360°，把它们拼起来，正好是一个圆。由此得出，涂色部分的总面积等于3个圆的总面积，即 3.14×12×3=9.42(cm2)。

【练一练】

1．例3的图3中，涂色部分的总周长是多少？

2．如图4，三角形每个角上的扇形的半径都是2cm，这三个扇形的面积之和有多大？

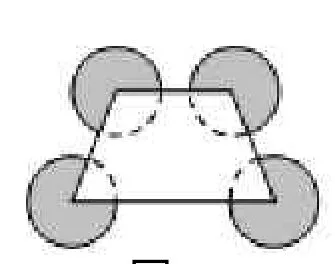
图3

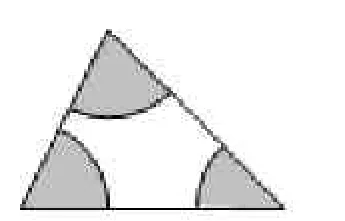
图4

《方程的妙用》参考答案：

明明的解法错在：三年前，这个人母亲的年龄是他的年龄的6倍。明明的方程中，写的是三年前母亲的年龄是这个人现在年龄的6倍。正确的方程：（x－3）×6=(33－3)。即：6x －18=30，6x=30+18，6x=48，x=48÷6=8，所以这个人今年8 岁了。

怎样来分呢？我仔细琢磨了一番后，找到了两种解法。

【解法一】借来1头牛，构建单位“1”。此题若按分数应用题的方法来解，由于17不是三个分数分母的公倍数，所以每人不能分得整数头牛。经试算，我发现，18与17相差1。如果邻居先借来1头牛，正好是18头牛，将18头牛看成单位“1”，那么问题就好解决了。

刚好可以把借来的1头牛还给人家。

【解法二】按三人所占的份数比来分配。根据遗言可知，大儿子占的份数是，二儿子占的份数是，小儿子占的份数是，他们所占的份数比是∶∶＝9∶6∶2，总份数是9＋6＋2＝17（份），大儿子分得，二儿子分得，小儿子分得。所以三个儿子分得的牛的头数分别为：

《整体入手 巧妙解题》练一练参考答案：1.26.84cm 2.6.28cm2

《巧设未知数》练一练参考答案：1.最轻的箱子重20千克。2.原有红球比白球多106个。