回转圆筒内粉体均化过程数值计算

韩坤何建铧 彭东辉 何洁宁 李志刚 徐静安

（上海化工研究院)

回转圆筒内粉体均化过程数值计算

韩坤*何建铧 彭东辉 何洁宁 李志刚 徐静安

（上海化工研究院)

采用Euler-Euler多相流模型，建立了回转圆筒内气-固-固三相流动守恒方程，对两种粉体的混合均化过程进行了数值计算。计算结果表明：随着回转时间的增长，两种粉体的最大体积分数均逐渐下降，直至理论均值附近；不同时刻样本均值始终围绕理论均值波动，但样本方差逐渐减小并趋于平稳。计算结束时，滑石粉体积分数的样本方差为0.001 01，均值为0.499 55，与模拟计算理论均值0.5相比误差-0.1%，符合工程要求，计算模型有效。

三相流 Euler模型 均化过程 体积分数 粉体 回转圆筒

符号说明

α——相体积分数；

ρ——相密度，kg/m3；

μ——相运动黏度，m2/s；

P——所有相共享的压力，Pa；

Ps——固体相的固体压力，Pa；

K——相间动量交换系数;

e——相间归还系数；

Cfr——相间的摩擦系数；

d——固体颗粒的直径，m；

g0——径向分布系数；

i、j——第i或j相。

0 前言

粉体混合均化过程是粉体工业生产操作过程中的核心工段。多年来，粉体均化技术已逐渐由之前的经验性设计发展到根据粉体混合机理[1-2]、物性来开发设计新型混合设备，并取得了一些成果[3-4]，但开发周期过长且过程繁琐始终是待突破的难点之一。利用数值计算软件对均化过程进行模拟，可在一定程度上确定较优参数并指导设计，目前此类研究多限于以离散单元法（discrete element method，DEM）开展，并在双锥型混合器[5]、回转干馏炉[6]等设备上获得了良好应用。但对微米级粉体颗粒而言，采用离散单元法计算量巨大，且因侧重颗粒碰撞而弱化了宏观流动形态。采用CFD软件有助于解决以上问题，但该类研究多限于粉体气力输送混合[7]，且以模拟计算气固两相流居多，回避了复杂而接近实际的气-固-固三相流。

本文以回转式粉体混合均化过程为研究对象，建立回转筒内粉体均化过程数值计算模型并对计算结果进行实验验证。

1 数值计算模型及算法

本文采用滑石粉和小苏打以等体积混合法建立物系，其物性参数见表1。数值计算以图1所示的回转筒内部空间为研究对象，以试验数据回归确定的最优工艺（回转速度8.6 r/min、回转时间20 min、填充率23.4%和抄板角度147°）作为本次数值计算的工艺参数。

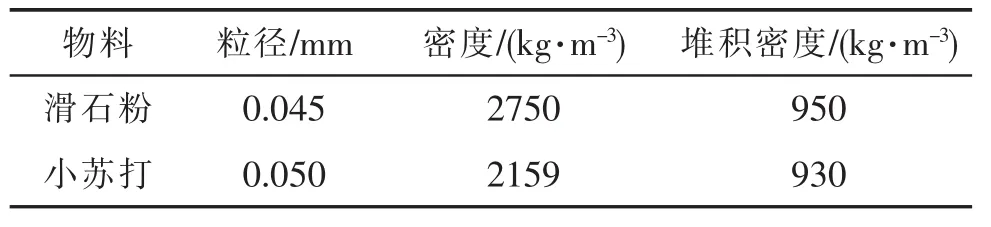
表1 粉体物料基本物性

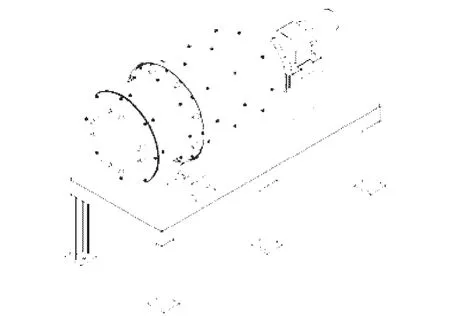
图1 回转圆筒混合器三维结构

1.1 计算模型

数值计算基于Euler-Euler多相流体模型，分为气（空气）－固（滑石粉）－固（小苏打粉体）三相。粉体均简化为球形，计算模型如下所述。

1.1.1 连续性方程

各相体积分数服从下述的连续性方程：

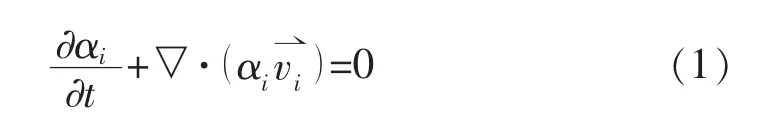
1.1.2 动量方程

动量方程分为气-气、气-固和固-固动量方程。回转筒内粉体流动所受的力主要有重力和外部体积力，忽略升力和虚拟质量力。写成通用的动量方程为：

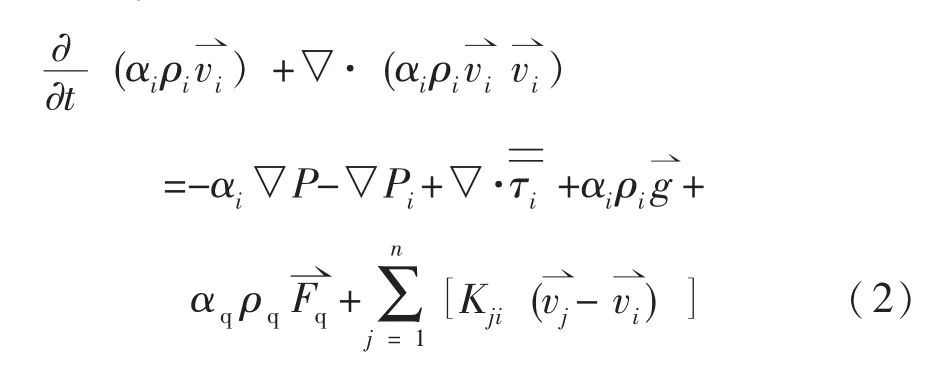
式(2)中，当i为气相时，▽Pi=0。计算采用multi-fluid granular model来描述气体-固体的混合行为。固体相应力来自于颗粒碰撞产生的随机粒子运动，该运动与气体分子热扩散类似，并假定颗粒相无伸缩特性。颗粒速度波动的强度决定了应力、黏度和固相的压力。

1.1.3 相间交换系数

模型不涉及气-气相间交换，对于气-固和固-固相间交换系数计算公式如下。（1）气-固交换系数当αj≤0.8时，

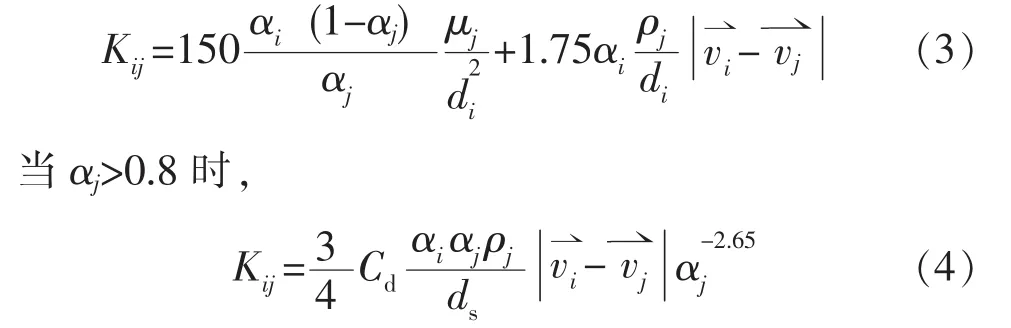
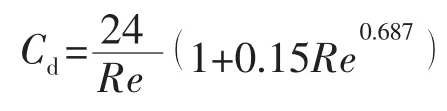
（2）固-固间动量交换系数

固-固间动量交换系数可按式（5）计算：

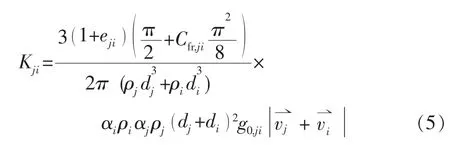
1.2 计算控制

求解过程为非稳态迭代计算，时间步长0.02 s，时间步内最大迭代次数为20次，回转时间为20 min，由此计算步数设定为60 000步（1200 s÷ 0.02 s/step=60 000 step）。计算迭代次数共计不超过60 000×20=1 200 000次。考虑到模拟计算过程的复杂性及耗时性，每个时间步内的收敛精度采用常用值，即连续性方程、动量方程、κ-ε方程中相关参数精度小于10-3收敛。

2 计算结果与讨论

2.1 粉体体积分数随时间的变化云图

图2～图5所示为0 s、1 s时刻的滑石粉体积分数云图。可以发现，随着回转圆筒的顺时针旋转，滑石粉逐渐开始滑动，在达到滑石粉的安息角后，物料开始滑落，覆盖在小苏打物料的料床表面上，并逐渐聚集成堆。这点与纯流体的混合情况完全不同，说明粉体拟流体假设既区别于纯流体，也区别于纯固体，符合粉体物性的两重性。

图2 0s时滑石粉体积分数云图

图3 0s时小苏打体积分数云图

图4 1s时滑石粉体积分数云图

图5 1s时小苏打体积分数云图

图6～图9依次为60 s、360 s、720 s及1200 s时滑石粉体积分数云图。可以发现，随着时间的推进，粉体最大体积分数逐渐下降，降至理论均值附近后平稳。其变化过程如图6～图9所示。

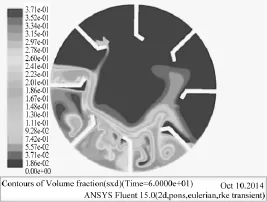
图6 60s时滑石粉体积分数云图

2.2 定量分析粉体体积分数变化情况

利用云图可以对模拟结果进行定性分析，简单直观、清晰明了，但定性分析不涉及详细结果数据，而定量分析往往更具准确性和说服力。为详细研究滑石粉与小苏打混合效果随时间的变化情况，将旋转区域X方向及Y方向分别按照200 mm的间距进行等分，则可以划分为如图10所示的16个区域。根据实验观察及云图显示，在运动过程中，滑石粉及小苏打主要存在于左下侧区域，即9、5、1、2、3区。

图7 360s时滑石粉体积分数云图

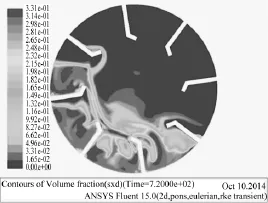
图8 720s时滑石粉体积分数云图

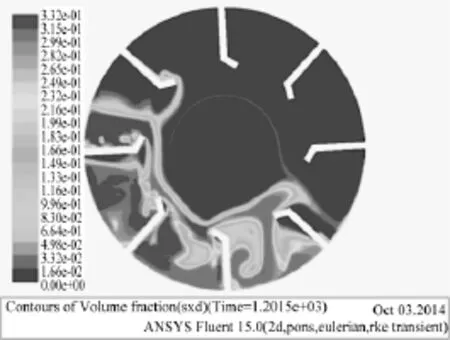
图9 1200s时滑石粉体积分数云图

定性计算考察混合均化过程中粉体体积分数（平均值）随混合时间的变化情况，由于粉体均化过程中单个粉体运动随机性较大，考虑到数据处理，选择左下侧5个物料混合区域各随机取点2次，获得滑石粉10组体积分数，然后对数据进行计算处理，计算得出滑石粉在不同时间点上的均值与标准差。完全混合的情况下，滑石粉体积分数的均值应为50%，标准差理论值为0。

图10 回转筒空间区域划分

图11所示为滑石粉体积分数均值及方差的变化曲线。模拟计算所取样本的均值与方差曲线较为平顺，最终样本方差数值为0.001 013 736。

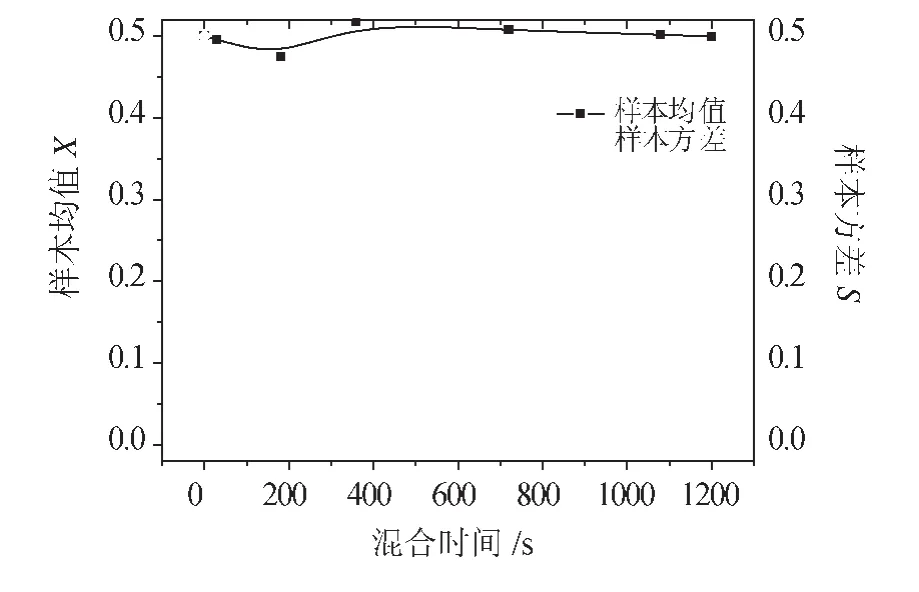
图11 滑石粉体积分数变化曲线

计算时，首先观察样本均值随时间的变化情况，可以发现其围绕50%上下波动，变化不大，说明5个取值区域基本代表了粉体物料的均化状态。计算结束时，滑石粉体积分数为0.499 55，与模拟计算理论均值0.5相比，误差-0.1%；与真实试验的样本均值0.497 2相比，误差1.55%，符合工程要求。

但均值曲线无法表征混合程度的进展情况，信息量较少，而采用方差却可有效表征。混合初期，滑石粉的体积分数采样值比较杂乱，波动较大，导致其样本方差较大。随着混合时间的增加，样本方差呈现逐渐下降的趋势，说明粉体的混合程度偏向均匀化。随着时间进一步增加，其方差的变化趋势逐渐平稳，说明粉体混合均化程度变化不大。最终滑石粉体积分数样本方差为0.001 01，该数值已基本满足工程应用要求。

3 结论

本模拟首先对物料混合进行理论分析，建立欧拉多相流数学模型，制定求解方法并开展计算；然后对计算结果进行定性和定量分析，并将模拟数据与试验数据进行对比。具体得到如下结论：

（1）均化过程初期滑石粉（或者小苏打）的流动情况表明，粉体具有两重性，其流动既区别于纯流体，也区别于纯固体。

（2）粉体最大体积分数随回转时间的增长而逐渐下降，降至理论均值附近后变化不再明显，说明回转筒内粉体浓度均呈现下降趋势。

（3）不同时刻样本均值围绕理论均值波动，但样本方差逐渐减小并趋于平稳，说明粉体混合趋于均匀。

（4）与试验参数对比发现，滑石粉体积分数与模拟计算理论均值相比，误差均小于10%；与实验所测样本均值相比，误差小于10%，符合工程化要求，计算模型验证有效。

[1]Chester A W，Kowalski J A，Coles M E,et al.Mixing dynamics in catalystimpregnation in double-cone blenders [J].Powder Technology，1999，102(1)：85-94.

[2]Brone D,Muzzio F J.Enhanced mixing in double-cone blenders[J].Powder Technology，2000，110(3)：179-189.

[3]欧阳鸿武，何世文，陈海林，等.粉体混合技术的研究进展[J].粉末冶金技术，2004,22(2)：105-108.

[4]厚美英，陈坤权.奇异的颗粒物质[J].新材料产业，2001(2)：6.

[5]江茂强.双锥型混合器内颗粒混合及增混机理研究[D].杭州：浙江大学，2010.

[6]张立栋.回转干馏炉内油页岩颗粒混合运动特性试验与数值模拟[D].北京：华北电力大学，2011.

[7]叶涛.多组分粉体混合过程的理论分析与实验研究[D].武汉：武汉理工大学，2009.

Numerical Calculation of Powder Homogenizing Process in Rotary Cylinder

Han Kun He Jianhua Peng Donghui He Jiening Li Zhigang Xu Jingan

Euler-Euler multiphase flow model was used to establish the conservation equations for gas-solidsolid there-phase flow in rotary cylinder,the numerical calculation of the two powders homogenizing process was carried out.The results show that the maximum volume fractions of powders gradually decreased to the theory average values along with the rotating time.The sample average values waved around the theory average value in different time,but sample variance gradually decreased and tended to be stable.When calculation finished,the sample variance of volume fractions of talcum powders was 0.001 01 and the sample average value was 0.499 55, the relative error was-0.1%compared with the theory average value of 0.5.The results satisfy with engineering requirements and the calculation model is proved valid.

There-phase flow;Euler model;Homogenizing process;Volume fraction;Powder;Rotary cylinder

TQ 027.1

2014-11-28）

*韩坤，男，1983年生，硕士，工程师。上海市，200062。