体外预应力加固铁路盖板涵应力增量分析

崔建龙，王起才，李盛，杨阳

(兰州交通大学土木工程学院，甘肃兰州730070)

体外预应力加固铁路盖板涵应力增量分析

崔建龙，王起才，李盛，杨阳

(兰州交通大学土木工程学院，甘肃兰州730070)

构建了顶板底部直线布置体外预应力筋加固盖板涵的计算模型，利用盖板涵加载变形前后的几何关系，探讨体外预应力筋应力增量与梁体挠度及混凝土压应变的关系，推导出了铁路运营阶段体外预应力加固盖板涵体外筋应力增量的表达式。可用该式计算在三分点荷载、均布荷载和集中荷载作用下用跨中挠度及混凝土压应变表达的体外筋应力增量。通过室内试验和相关文献验证了本文表达式的正确性，可为体外预应力加固盖板涵结构设计提供指导。

盖板涵 体外预应力 应力增量 参数分析

随着我国铁路运量的不断增加，盖板涵出现的病害日益突出［1-2］，对既有盖板涵结构进行加固实现重载运营日趋重要。相比其他加固形式，体外预应力加固优点在于不仅能大幅度提高承载能力和改善结构性能，而且施工工期较短，最大可能地减少对既有铁路运营的干扰。而体外筋应力增量的计算在研究体外预应力结构力学性能中凸显重要［3］。体外预应力筋应力增量不能由平截面假定来确定，而与结构的变形有关［4-6］，国内外学者进行了大量的试验及理论研究。Naaman教授等［7］通过黏性折减系数实现截面应变相容，从而确定极限应力增量。我国规范及其他规范［8-9］根据大量试验研究，回归建立了基于截面配筋率的极限应力增量经验公式。这些研究方法主要依靠试验结果，对承载能力极限状态建立体外预应力筋应力增量的计算公式。杜进生［4］、贺志启、王景全等［5-6］依据结构受力机理，基于结构变形应力增量分析，建立了承载能力极限状态和正常使用状态下用跨中挠度表示的体外预应力筋应力增量统一计算公式。该公式能较好地反应结构的受力机理，但推导过程近似取截面形心轴为中性轴，将此公式用于截面高度比较低的体外预应力加固盖板涵结构是不太准确的。此外，有关铁路运营阶段预应力筋应力增量的计算很少有系统分析。故本文借助大秦线体外预应力加固盖板涵这一课题，针对采用梁底直线布筋形式，通过挠曲线微分方程得到梁跨中挠度与梁端截面转角的几何关系式，并推导出不同荷载作用形式下的应力增量统一算法。结合室内试验结果与本文公式进行了数值对比，进一步验证铁路运营阶段体外筋应力增量统一算法的可靠性。

1 理论推导

根据盖板涵的力学特点，在推导过程中做以下假设:①在弹性工作状态下，体外预应力筋引起的二次效应忽略不计;②盖板涵受弯后，截面应变符合平截面假定，不考虑受拉区混凝土的作用;③锚固区长度等于顶板的计算跨径。

1.1 体外预应力筋应力增量推导

对于在梁底直线布筋且不设转向块的体外预应力加固分析模型如图1所示。应力增量表达式为

1)均布荷载下的应变增量

均布荷载下梁体产生的弯矩M(x)为

式中:ΔTp为有效预应力增量;dp为顶板厚度。

根据梁的近似挠曲线微分方程EIw″=-M(x)积分得

式中:E为混凝土弹性模量;I为截面换算惯性矩;D为积分常数，由边界条件确定。

通过梁体边界条件，梁端截面转角θ为

图1 体外预应力加固模型

假设转角θ与跨中挠度Δ满足关系式θ=k1Δ+ k2，跨中挠度Δ与跨中弯矩满足关系式通过整理计算得

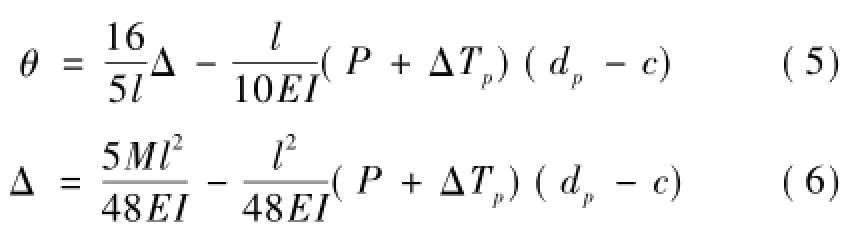
式中:ε为受压区混凝土应变。

将式(5)代入式(1)可得用挠度表示的应变增量表达式为

将式(7)代入式(8)可得基于截面应变的应变增量表达式为

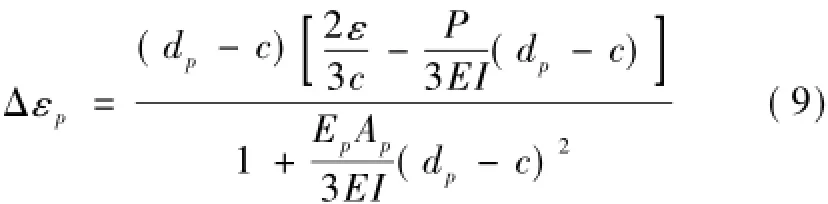
同理，可以推导出三分点荷载和集中荷载作用下的应变增量。

2)三分点荷载下的应变增量

三分点荷载作用下，用挠度表示的体外预应力应变增量表达式为

基于截面应变的应力增量表达式为

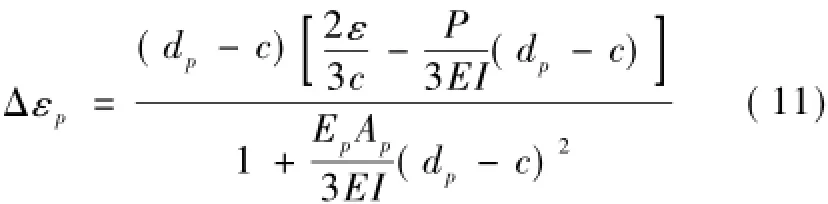
3)跨中集中荷载下的应变增量

对于跨中集中荷载作用下，用挠度表示的体外预应力应变增量表达式为

基于截面应变的应变增量表达式为

1.2 统一公式

对直线体外预应力筋应力增量的推导总结，可以归纳出均布荷载、三分点荷载和集中荷载作用下应变增量统一表达式。用挠度表示的体外预应力应力增量统一表达式为

基于截面应变的应力增量表达式为

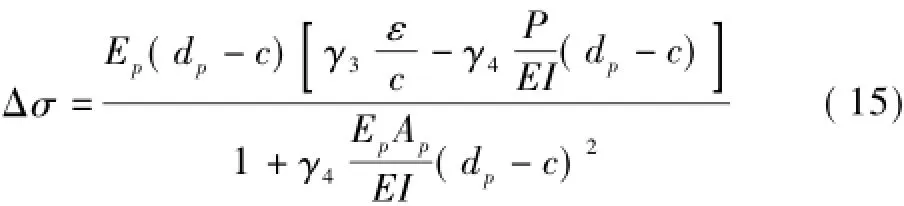
式中:P为有效预应力，kN;γ1，γ2，γ3，γ4为应力增量系数。其大小如表1所示。

表1 应力增量系数取值

2 试验验证

2.1 试验设计

为了验证本文推导体外预应力应力增量公式的准确性，根据相似原理自制跨径为4.5 m，宽度为1 m的盖板涵进行体外预应力加固后静载试验［10-14］。结构混凝土强度平均为35 MPa，弹性模量约为3.15× 104MPa，梁体内纵向受拉钢筋为18根φ16 mm，受压钢筋为6根φ8 mm。采用体外预应力筋加固，在距梁4 cm处设置3根直径25 mm的精轧螺纹钢筋，初始张拉力为70 kN。

室内试验加载设备采用液压千斤顶，在不同荷载等级下通过钢筋表面应变片测定梁体体外预应力增量的值，如图2所示。

图2 体外预应力加固模型

2.2 试验结果分析

由表2及图3可知，本文体外预应力筋应力增量计算结果与实测值比较接近，而文献［6］计算结果偏小，这是由于文献［6］预应力筋偏心距em近似取预应力筋与截面形心轴距离。而试验结果表明，截面受压区高度基本为125 mm，盖板涵截面形心轴与中性轴相差105 mm，对于梁高较小的盖板涵来讲，近似取值相对误差较大。因此，本文体外预应力筋应力增量计算方法对于采用梁底直线布筋的体外预应力加固盖板涵具有一定的适用性。

表2 不同方法计算的应力增量随施加荷载变化

图3 应力增量实测值与理论计算值的对比

3 参数分析

根据室内试验加固方式，主要从以下两个方面来考虑对铁路运营阶段体外预应力盖板涵应力增量的影响:①施加的有效预应力;②荷载形式。这些因素在本文推导的统一公式中均有明确反映。

3.1 有效预应力影响分析

混凝土为C35，梁体内纵向受拉钢筋为18根φ15 mm，体外加固采用3根φ16 mm精轧螺纹钢筋，距梁底面距离为40 mm，得到不同有效预应力的体外筋应力增量随加载等级的变化规律，如图4所示。

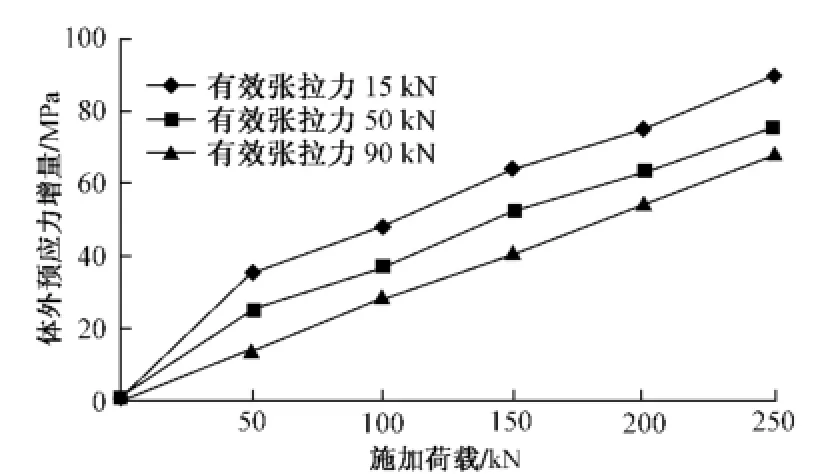
图4 应力增量随施加荷载等级变化规律

从图4可以看出，当施加不同有效体外预应力加固后，荷载从0增加到250 kN时，体外筋应力增量逐渐增大。当荷载达到250 kN时，有效预应力90 kN比15 kN应力增量减小24%。这主要是因为截面的中性轴高度降低，梁体的转动能力下降，故应力增量减小。

3.2 荷载形式影响分析

体外预应力筋张拉50 kN，得到不同荷载形式的体外筋应力增量随加载等级的变化规律，如图5所示。

图5 不同荷载形式的应力增量随施加荷载等级变化规律

从图5可以看出，不同荷载形式的盖板涵采用体外预应力钢筋加固后荷载从0增加到250 kN时，体外筋应力增量逐渐增大。当荷载达到250 kN时，集中荷载比三分点荷载应力增量增大16%。主要是因为集中荷载比三分点荷载在跨中截面产生的弯矩大，盖板涵截面转动能力大，故应力增量大。

4 结论

本文通过体外预应力公式推导和室内试验解决了铁路运营阶段盖板涵体外预应力加固的计算方法，并对影响盖板涵体外预应力加固效果的两种参数进行了分析，得到以下结论:

1)基于文献［4-6］推导了铁路运营阶段在盖板涵底布置直线体外预应力筋加固时，预应力筋应力增量的统一表达式，公式适用于不同荷载形式。通过与文献［6］计算结果和室内试验实测结果相比较，验证了本文计算结果具有足够的精度，能满足实际盖板涵体外预应力加固的工程要求。

2)提高体外预应力钢筋有效预应力对减小体外筋应力增量作用明显，同时可提高截面刚度、强度。实际工程中可根据减载要求，选择相应有效应力，避免有效应力过大引起梁体上拱，导致行车不安全。

3)盖板涵既有梁在不同荷载作用下，体外预应力筋应力增量不同，集中点荷载比三分点荷载引起的应力增量要大很多，在检算体外预应力加固过程中必须要考虑集中荷载作用下的不利影响。

［1］钱立新.国际铁路重载运输发展概况［J］.铁道运输与经济，2002(12):55-56.

［2］于本田，邹花兰，王起才.大秦重载铁路既有盖板涵病害调查与分析［J］.铁道建筑，2010(7):37-40.

［3］邱青云，童顺军.体外预应力混凝土桥梁的发展现状及探讨［J］.铁道标准设计，2000，20(5):19-20.

［4］杜进生.无粘结预应力混凝土结构——试验、理论及应用［M］.北京:机械工业出版社，2012.

［5］贺志启，刘钊，王景全.基于挠度的体外预应力梁应力增量统一算法［J］.土木工程学报，2008，41(9):90-96.

［6］王景全，刘钊，吕志涛.基于挠度的体外与体内无黏结预应力筋应力增量［J］.东南大学学报，2005，35(6):915-919.

［7］NAAMAN A E，ALKHAIRIFM.StressatUltimatein UnbondedPost-tensioningTendons:Part2-Proposed Methodology Culverts［J］.ACI Structural Journal，1991，88 (6):683-692.

［8］中华人民共和国建设部.JGJ 92—2004无粘结预应力混凝土结构技术规程［S］.北京:中国建筑工业出版社，2005.

［9］杜拱辰，陶学康.部分预应力混凝土梁无黏结筋极限应力的研究［J］.建筑结构学报，1985，6(6):2-13.

［10］姚谦峰，陈平.土木工程结构试验［M］.北京:人民交通出版社，2005.

［11］颜志华.体外预应力加固混凝土梁试验研究［J］.世界桥梁，2007(1):50-52.

［12］崔建龙，王起才，李盛，等.体外预应力加固重载铁路盖板涵试验研究［J］.铁道标准设计，2011(4):66-70.

［13］崔建龙，王起才，李盛，等.体外预应力加固铁路盖板涵静载试验研究［J］.铁道建筑，2014(7):31-33.

［14］崔建龙，王起才，李盛，等.基于Ansys体外无粘结预应力筋加固铁路盖板涵静载分析［J］.铁道标准设计，2015 (3):78-81.

Analysis of stress increment in railway slab-culvert due to reinforcing by external prestressing

CUI Jianlong，WANG Qicai，LI Sheng，YANG Yang
(1.College of Civil Engineering，Lanzhou Jiaotong University，Lanzhou Gansu 730070，China)

A model of a slab-culvert strengthened with external prestress in the bottom was established.T he culvert deformations before and after the loading were investigated.T he relationship among the stress increment in prestressing strands，the deflection and the compression stress in concrete was studied.An expression for this stress increment in railway operation stage was deduced.T he expression can be used to calculate the mid-span deflection and the stress increment in prestressing strands in the case of three-point loading，uniform loading or concentrated loading.T his expression proved correct through lab test and previous references，and it can provide guidance for culvert structure strengthened with external prestress.

Slab-culvert;External prestress;Stress increment;Parametric analysis

U445.7+2

A

10.3969/j.issn.1003-1995.2015.05.07

1003-1995(2015)05-0026-04

(责任审编赵其文)

2014-07-10;

2015-03-09

长江学者和创新团队发展计划资助项目(IRT1139);铁道部科技研究开发计划项目(2012G011-A)

崔建龙(1989—)，男，甘肃天水人，硕士研究生。