基于灰色TOPSIS法的非常规突发事件应急决策研究

秦小楠 中国海洋石油总公司财务资产部

基于灰色TOPSIS法的非常规突发事件应急决策研究

秦小楠 中国海洋石油总公司财务资产部

近年来，非常规突发事件频发，给人民的生命财产带来极大的破坏和威胁。非常规突发事件的应急信息具有不确定性、不完全性的特点，其模糊信息的应急决策需要在权衡多个目标和属性的前提下进行。在综合考虑主观权重、客观权重和反馈权重的基础上提出一种综合权重，并结合灰色关联度对TOPSIS方法进行改进，得出一种创新性的多目标应急决策方法。最后通过日本核事故的实例进行分析，验证了该方法的可行性和有效性。算例证明，灰色TOPSIS法为非常规突发事件的应急决策提供了一种新的工具和思路。

非常规突发事件；应急决策；TOPSIS法；灰色关联度

中国国家自然科学基金委员会（NSFC）在2009年确立了一项非常规突发事件的重大研究计划，全国共申报126项，其中应急决策占48项，这代表着国内非常规突发事件应急决策领域的研究进入快速发展阶段。张锦、蔡琦等[1]综合各个评价指标的主、客观权重来优化改进传统的TOPSIS法，建立了多属性决策模型；翟丹妮、崔恒旋等[2]在主、客观权重的基础上，结合反馈权重提出了一种基于反馈机制的改进TOPSIS法，并建立突发事件应急决策方案优选决策模型；邬文帅、寇纲等[3]结合灰色系统理论和多目标决策理论提出了一种改进的模糊多目标应急决策方法，并利用三角模糊数来处理信息的模糊性和不确定性。以上研究都对传统的应急决策方法有一定创新，包括指标权重的创新、决策方法的改进等，而本文将综合权重、灰色关联度、TOPSIS法三者相结合，提出一种改进的灰色TOPSIS法，并以日本核事故为案例，选取合理的指标，赋以综合权重，利用改进的灰色TOPSIS法制定应急决策方案并进行评价，根据各方案执行结果选择最优方案。

1 非常规突发事件应急决策模型的构建

TOPSIS法即逼近于理想解排序法，由Hwang C.L.和Yoon K.于1981年提出[4]，经过近30年的发展逐步成熟，并广泛应用于多个领域来解决多目标决策问题的方案优选问题。其基本原理是根据多个指标确定正负理想解，并计算每个方案到正理想解和负理想解的距离，最后据此进行排序，选出最优方案。

非常规突发事件应急决策模型的构建首先需要选取决策方案的评价指标并建立标准化决策矩阵，其次是对评价指标赋以权重，最后通过TOPSIS法进行方案的优选[5]。

1.1 应急决策方案评价指标的选取

决策方案指标主要分为效益型指标和成本型指标两种。顾名思义，效益型指标越大，说明该决策方案产生的效益越大；成本型指标越小，说明执行该决策方案花费的成本越小。二者都可用实数型、区间型和语言型来表示，其中语言型是转化为三角模糊数来计算。本文采用统一的实数型来表示。

1.2 原始决策矩阵的建立与规范化处理

设应急备选方案的个数为a，每个方案评价指标的个数为b，以初始数据为基础，建立原始决策矩阵[3]

原始决策矩阵建立之后需要对其数据进行规范化处理，防止因指标量纲等的不同造成结果和方案的可信度不高，因此需要对原始决策矩阵进行归一化处理，得到规范化矩阵

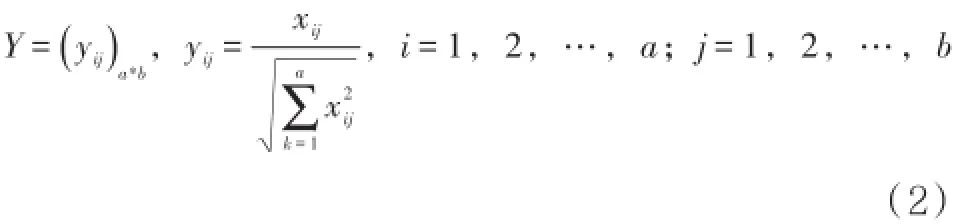
1.3 指标权重的确定

各个指标分别反映某个决策单位的标准，但一般意义上来讲各个指标属性的重要性是不同的，因此要对各个指标赋予不同的权重。本文采用一种新的综合权重确定方法，结合主、客观权重和反馈权重得出各指标权重，这样使得权重确定的过程和结果更加科学和全面，更有利于决策者在最短的时间内选择合理的应急方案[6]。

综合权重公式如下

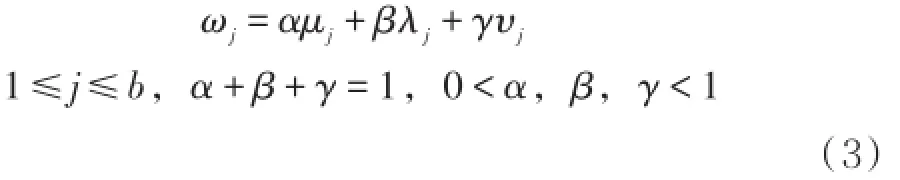
式中μj为主观权重，λj为客观权重，υj为反馈权重。主观权重通过AHP层次分析法来确定；客观权重以各方案到理想点距离的加权平方和作为综合评价的依据，如式（4）；反馈权重则是根据以往方案实施的方式和效果得出，如式（5）。

式（4）中，di、λj和y*j分别为方案i与理想解的距离、指标j的客观权重和理想解。通过MATLAB软件对此非线性优化模型求解。

式（5）中，a为已执行方案的个数；di为各方案贴近度与方案满意度的差值；vj表示j指标的反馈权重；分别表示j指标的正理想解和负理想解；分别表示第i个方案到正理想解和负理想解的距离；Ci表示第i个方案的贴近度；Ui表示第i个方案的满意度。

1.4 最优决策方案的选择

指标权重确定之后还要对每个方案的实施结果进行评价，从而选出最优方案。根据TOPSIS基本原理可知，最优方案选择需要首先确定加权矩阵、正理想解、负理想解，随后计算灰色关联系数、灰色关联度和灰色关联贴近度，从而确定最优方案[7-9]。

第一步：确定加权矩阵。

根据综合权重，确定加权标准化矩阵Z

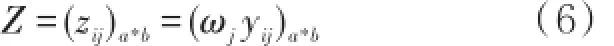
第二步：确定正理想解与负理想解

第三步：计算第i个方案与正理想方案关于第j个指标的灰色关联系数

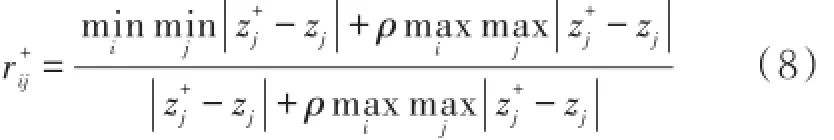
其中ρ为分辨系数，取值为0.5。则各个方案与正理想方案的灰色关联系数矩阵为第i个方案与正理想方案的灰色关联度为

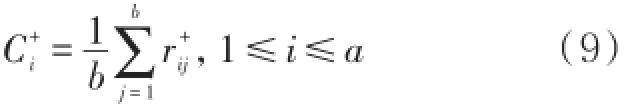
第四步：同理可得，第i个方案与负理想方案的灰色关联度为

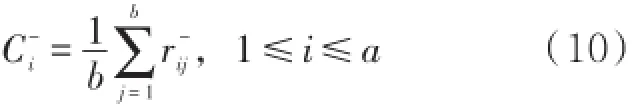
第五步：计算各个方案的灰色关联相对贴近度

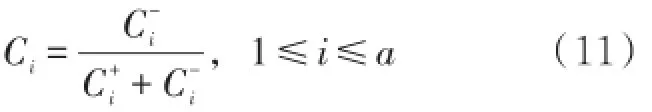
灰色关联相对贴近度描述的是每个方案的优劣程度，相对贴近度越大，表明该方案越优；相对贴近度越小，表明该方案则越差。综上对TOPSIS的改进可以看出，本文改进灰色TOPSIS法与传统的TOPSIS方法的主要区别有以下两点：第一，在指标权重确定方面综合了主、客观权重，同时引进了反馈权重，使得决策更加科学、全面；第二，引入灰色关联度计算被选方案与正负理想方案的距离，考虑到了方案之间的关联程度，突出指标间的相互联系，最后用灰色关联相对贴近度来表示方案的优劣程度，为多目标决策提供了有力的决策分析工具。

2 日本核泄漏事故应急决策应用实例

及时准确的应急决策是成功进行应急管理的核心要素，对于提高应急管理能力和水平有着重要作用。2011年3月11日，日本地震引起的福岛核泄漏事故对社会和环境造成了极大的危害，本文以此为实例来验证灰色TOPSIS法的可行性和有效性。首先通过专家确定四个方案：去污、避迁、去污+避迁、永久再定居，各应急方案评价指标见表1。

根据表1得出原始矩阵

表1 各应急备选方案评价指标

根据公式（2）将其标准化得出规范化矩阵

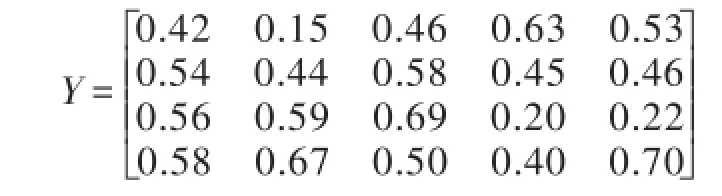
得出主观权重μ=[0.295 0.263 0.357 0.214 0.099]，客观权重λ=[0.227 0.082 0.323 0.069 0.136]。

为得到决策方案各指标的反馈权重，特提出假设：案例库中四种方案均执行过一次，表2所示为各方案的执行结果。

利用表2的数据，再结合式（5）求得反馈权重υ=[0.316 0.124 0.336 0.194 0.120]。将主观权重、客观权重和反馈权重数据代入式（3）求得综合权重，同时假设三种权重的重要程度分别为0.2、0.2、0.6，得综合权重ω=[0.256 0.152 0.311 0.126 0.093]。随后确定加权标准决策矩阵，利用式（7）、（8）、（9）解得正、负理想解，灰色关联系数及灰色关联系数矩阵，以此确定灰色关联度，最后根据式（11）求出各方案的灰色关联贴近度为：C=[0.612 0.536 0.726 0.467]。

表2 各方案执行结果

根据灰色TOPSIS法的原理可知，各方案的灰色关联贴近度越大，方案越优。通过以上计算结果可知：日本核泄漏事故应急决策方案优选顺序为方案三、方案一、方案二、方案四，故最优方案为方案三，即去污和避迁两项工作同时进行，其次是方案一去污，第三是方案二避迁，最后是方案四永久再定居。

3 结论

在非常规突发事件发生后的“贫信息”情况下，迅速准确的应急决策可以极大地促进应急工作的开展，对于减小损失具有至关重要的意义。本文提出了一种基于综合赋权法和灰色关联理论的灰色TOPSIS法，并通过日本核泄漏的实例验证了灰色TOPSIS法的可行性和有效性，为非常规突发事件应急决策提供了参考，也提出了一套新的工具和思路，同时丰富了非常规应急管理领域的研究。

[1]张锦，蔡琦，张帆，等．改进的TOPSIS法在核电站事故应急决策中的应用[J]．辐射防护，2009（3）：184-188.

[2]翟丹妮，崔恒旋，段冉，等．改进的TOPSLS法在突发事件应急决策中的应用[J]．风险管理，2013（4）：14-18.

[3]邹文帅，寇纲，彭怡，等．面向突发事件的模糊多目标应急决策方法[J]．系统工程理论与实践，2012（6）：1 298-1 304.

[4]Hwang C L，Yoon K.Multiple Attribute Decision Making[M]．Berlin：Springer-Verlag，1981.

[5]程平，刘伟．多属性群决策中一种基于主观偏好确定属性权重的方法[J]．控制与决策，2010（11）：1 645-1 656.

[6]丁浩，张朋程，刘玲，等．混合型多属性群决策的油田节能项目优选模型——基于Value集TOPSIS方法的研究[J]．中外能源，2012（3）：93-98.

[7]陈兴，王勇，吴凌云，等．多阶段多目标多部门应急决策模[J]．系统工程理论与实践，2010，30（11）：1 977-1 985.

[8]Jahanshahloo G R，Hosseinzadeh Lotfi F，Izadikhah M.Extension of the TOPSIS method for decision-making[J]．China Environmental Science，2011，31（5）：876-880.

[9]徐泽水．权重信息完全未知且对方案有偏好的多属性决策法[J]．系统工程理论与实践，2003，23（12）：100-103.

（栏目主持 李艳秋）

10.3969/j.issn.1006-6896.2015.9.010

秦小楠：高级会计师，主要研究方向为信息化管理、计划投资管理。

2015-08-20

18266636275、upcjgyxwjm@163.com