基于激光雷达的移动机器人避障规划仿真研究

刘 杰，闫清东，唐正华

(1．北京理工大学机械与车辆学院，北京100081;2．装甲兵学院模拟训练中心，安徽蚌埠233050)

1 概述

避障是自主移动机器人系统能否成功应用的关键问题之一，目前对于避障问题的研究已经形成了很多成熟的理论，矢量场直方图［1］(Vector Field Histogram，VFH)理论就是其中之一。

矢量场直方图是一种以超声波为探测器的机器人新的避障方法，该方法的提出解决了虚拟势场法(Virtual Force Field，VFF)［2］在实际应用中出现的数据激变问题，即合排斥力的方向和大小在栅格减少时会出现很大的变化。为了改进VFH算法在应用过程中存在的问题，文献［3］提出了VFH+算法，文献［4］将 VFH+算法进行了进一步改进，提出了VFH*算法。随后，国内的研究者提出了考虑障碍物速度的VFH#［5］算法以及完善初始环境信息提取的 PVFH 算法［6］。

然而，不论是 VFH的原始算法还是改进版本［7-9］，通过分析会发现一个最根本的问题是，算法是结合当时的环境设备提出的，即上述算法的环境传感器均为超声波探测仪，正是因为超声波传感器对环境信息的检测的不完全可靠性，使得研究者不得不提出各种处理数据的方法，如采用栅格化的数据信息以及设置置信度等手段，以应对其产生的大量的数据误差［10-11］。随着科技的发展，激光雷达的应用则完全可以解决数据精度带来的环境探测问题。为此，本文以二维激光雷达为环境探测仪，应用VFH算法的思想，对移动机器人进行室外避障规划的仿真研究。

2 算法设计

激光雷达采集的是以移动机器人为中心的极坐标系下的障碍物距离值，而VFH算法是将障碍物对移动机器人的影响量化为各个测量方向上的极线障碍强度值［12］。移动机器人会在低于确定阈值的角度范围内选择其移动方向，它的不足之处是阈值的设置需要依据移动机器人的实际运行状态，没有统一的理论。阈值过大时，将使一些可行通道被忽略，导致移动机器人不能通过狭窄的通道，丧失到达目标点的能力，如图1(a)所示;阈值过小时，移动机器人会难于发现前方的障碍物，高速行进时会由于来不及躲避障碍物而发生碰撞，如图1(b)所示。

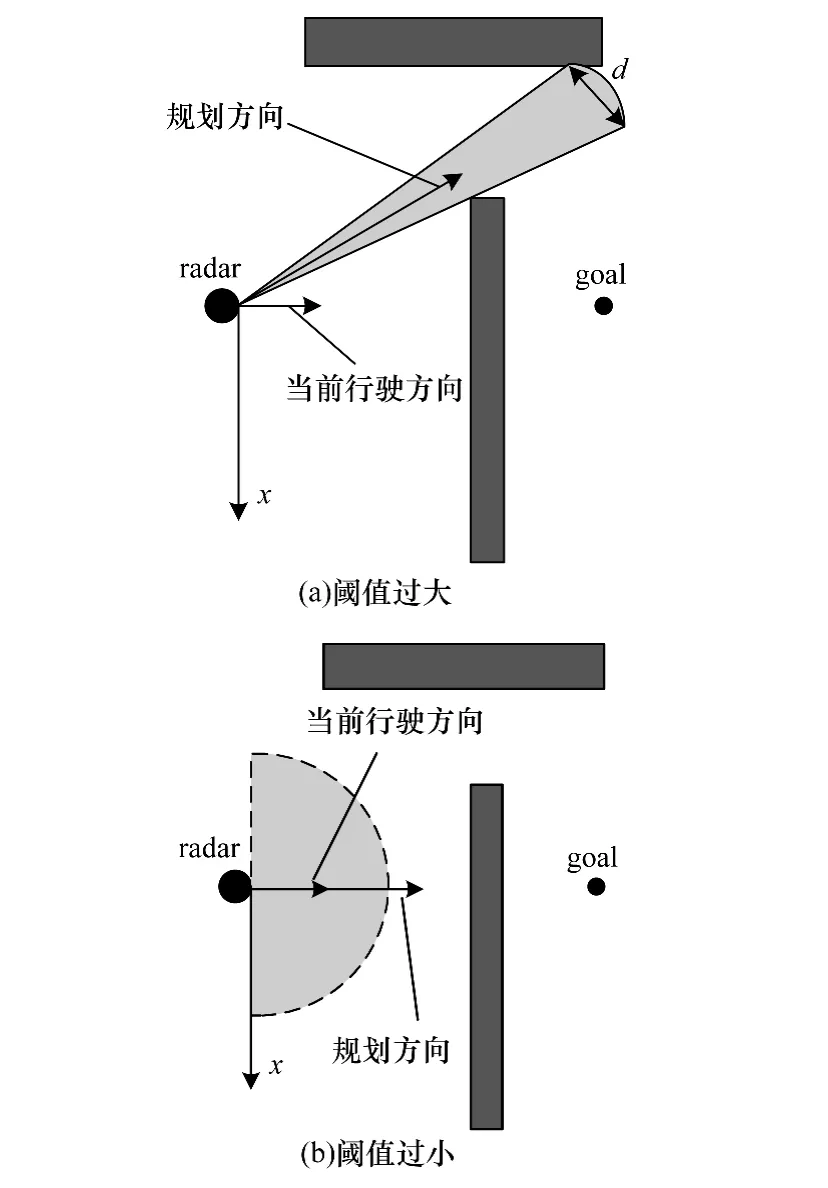
图1 阈值与避障的关系

2．1 坐标变换

激光雷达测距仪的量程选为180°/1°，即雷达每一次采集181个数据。根据激光雷达采集的环境数据，建立以激光雷达为中心的极坐标系下环境信息，为了规划机动平台的避障运行方向，需要对该极坐标系与机动平台行进的全局直角坐标进行坐标变换。变换规则如图2所示。图2展示了机器人的极坐标系与直角坐标系之间的位置关系。

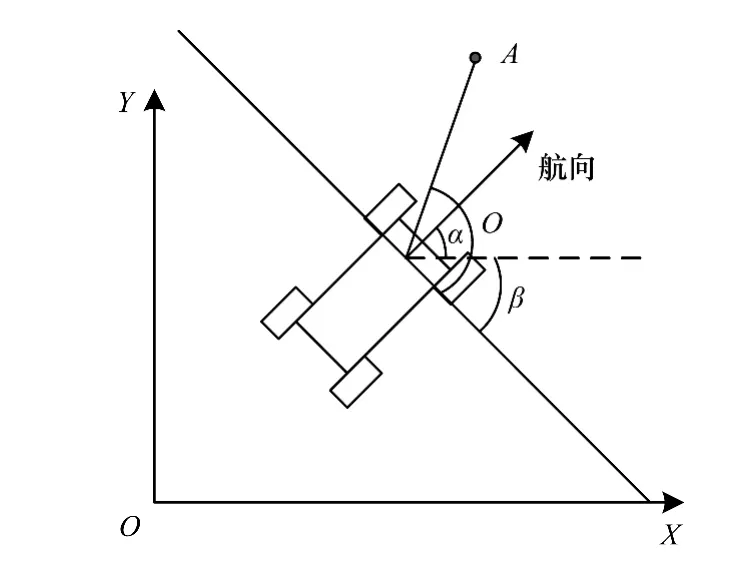
图2 坐标变换示意图

α为机器人在直角坐标系中的航向角，β为极坐标系-直角坐标系坐标变换角。

则已知极坐标系下障碍物A的方向角为O，其在直角坐标系系下方向角Φ表示为:

式(2)即为航向角的极坐标系与直角坐标系转换公式。

2．2 自适应阈值设置

本文的航向阈值设置规则如下:

其中，dsmax为可设置的最大阈值;drT为激光雷达与目标点之间的距离;Ni为自适应常数。当R为固定增量，ds0为非航向方向设置的相应阈值，定义如下:

其中，λ＞1为安全距离放大系数;D为机器人从最大速度状态减速到静止状态所行进的距离;a为减速加速度。假设机器人的 vmax=1．2 m/s，a=－1 m/s2，可得机器人的最短行驶距离D=0．72 m。为了保证安全，此处设置 λ=1．4。设 R=0．1，则ds0=1 m，dsmax=2．5 m。

2．3 自由扇区以及转向方向的确定

在建立了激光雷达极坐标环境地图之后，为了确定机动平台的最终避障行进方向，首先需要根据环境地图确定平台可通过的扇区区间，然后从中选取最适当的扇区区间，最后确定转向方向，具体步骤如下:

(1)自由扇区的确定

定义 在极坐标环境地图中，如果θ角度方向的距离 dθ＜ds，或者 dθ=ds且 dd＜0．5(0．5 为机动平台的车宽)，则该区域称为峰扇区;否则为谷扇区，亦称候选波谷。其中，dd的定义如下:

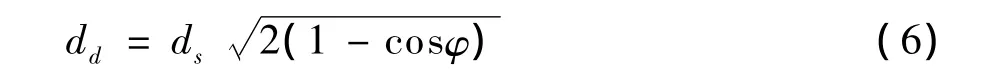
其中，φ为包含θ在内的连续dθ＞ds区域的角度值。

依据上述定义确定的谷扇区即称为自由扇区，亦即机动平台可通行的方向。

(2)平台转向方向的确定

首先，在平台直角坐标系下，利用式(7)计算目标点与机动平台的夹角α，如图3所示。

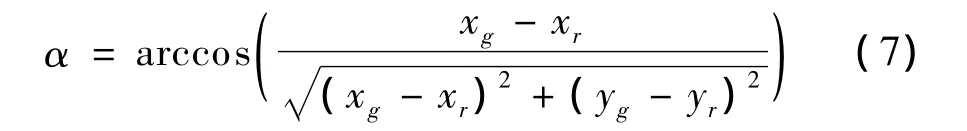
其中，(xg，yg)和(xr，yr)分别为目标点与激光雷达的当前直角坐标系下的直角坐标。通过坐标变换，将α转换到以激光雷达为中心的极坐标系，并用α1表示。

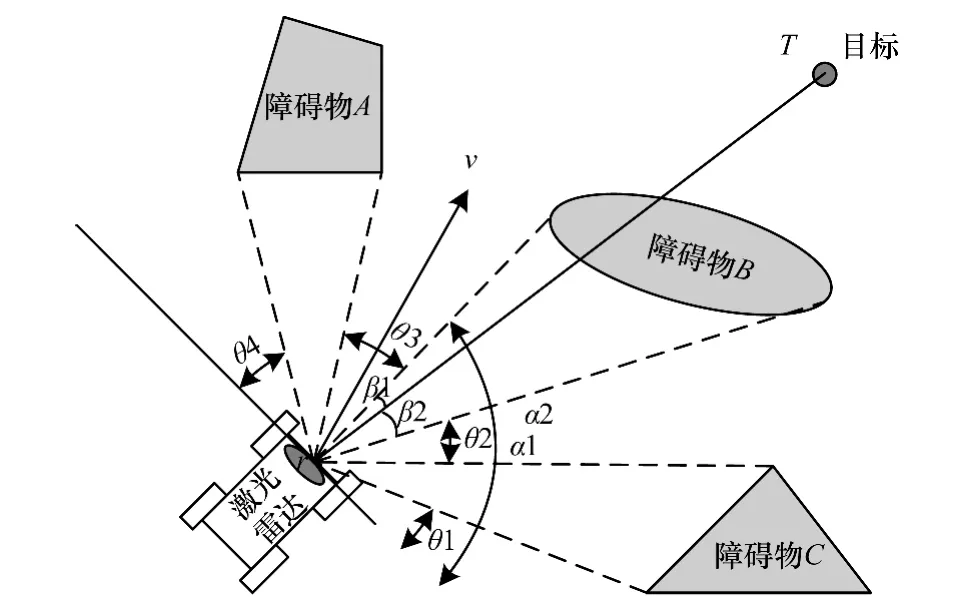
图3 测量位置关系示意图

由图3可知，drT恰好经过障碍物B，因此，设置障碍物B的数据阈值为dsmax=2．5 m。而障碍物A与障碍物C的数据阈值设为dsmax=1．5 m，该阈值主要是为了避免机器人与障碍物发生碰撞。

经过转换，从极坐标环境示意图中可以看出，在机动平台的前方共有4 个候选方向:θ1，θ2，θ3，θ4。而与r－Target方向最接近的2个扇区的角度为θ2与θ3。同时，通过计算得知，2个扇区均为自由扇区，可以作为机动平台的候选航向。分别计算2个候选扇区与O－Target方向的角度差β1与β2，通过比较可以得知β1＜β2，即通过θ3扇区到达目标点行程更近，因此，确定θ3扇区为机动平台的最终航向扇区。

(3)转向角度的计算

已知θ3扇区的起始方向OB的角度为α1，终止方向OC的角度为α2，则最终确定在激光雷达极坐标系下，机动平台的行进方向为φ:

则最终机动平台的航向为:

3 仿真实验与结果分析

根据上述算法设计规则，避障控制算法的控制流程如图4所示。仿真实验是在机器人仿真器MobileSim中进行，通过Mapper3软件构建机器人的环境地图，并导入MobileSim中。在VS2010开发环境中，通过C++编程实现算法控制。

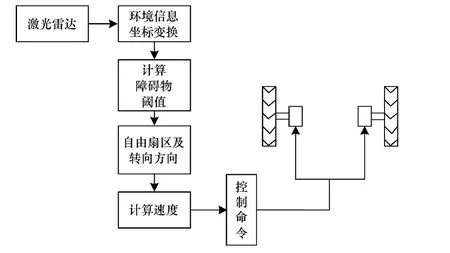
图4 控制算法流程

移动机器人的起点坐标为(0，0)，终点坐标为(12 000，8 000)，单位为mm。图中杂乱无章放置的多边形棕色区域表示环境中的障碍物。初始航向角设置为0°，行进过程中以匀速行驶，框图曲线表示移动机器人在避障规划中的行进路线。仿真环境设置如图5所示，图中为机器人行进过程中，激光雷达的数据测量过程。

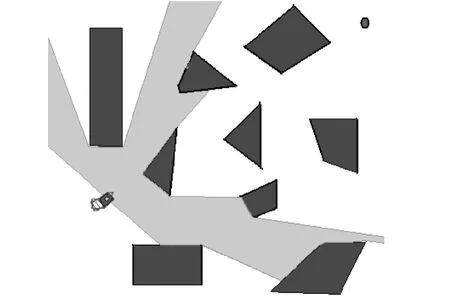
图5 仿真环境中的激光雷达探测环境信息

图6(a)到图6(e)分别给出了不同行驶速度下，移动机器人的避障规划结果。障碍物避障阈值统一设置为2 500 mm，从图6(a)到图6(e)对应的行驶速度 分 别 为 400 mm/s，700 mm/s，800 mm/s，900 mm/s以及 1 000 mm/s。

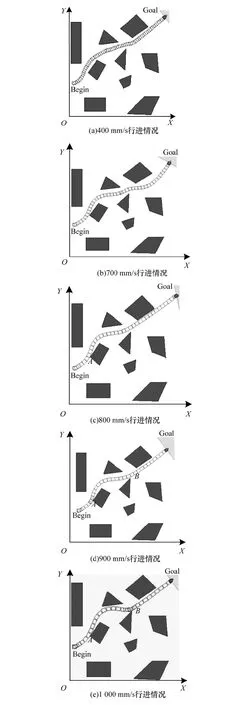
图6 移动机器人的避障规划结果

由仿真曲线可知，移动机器人的行进速度低于800 mm/s时，应用本文提出的避障算法都可以顺利地穿越障碍物区域到达目标点。当行驶速度大于800 mm/s时，算法控制的机器人亦会到达目标点，但是移动机器人在行驶过程中与障碍物会发生轻微的碰撞，如当800 mm/s行驶时，机器人在障碍物A点处恰好绕行;当行驶速度为900 mm/s时，机器人会与障碍物A点发生轻微碰撞，而恰好绕行障碍物B点;当行驶速度达到1 000 mm/s时，机器人则会与障碍物A点以及障碍物B点都发生轻微的碰撞。图7给出了机器人行驶速度高于800 mm/s时，机器人的航向角变化情况;由图可知，随着移动机器人行进速度的增大，机器人在行进过程中航向角的变化幅度是增加的。

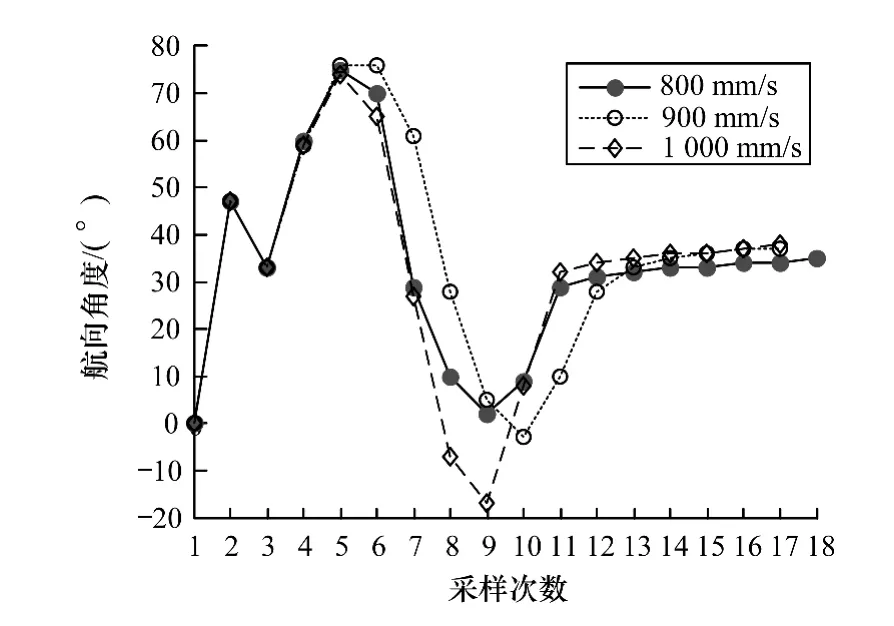
图7 避障过程航向角变化曲线

仿真过程中发现，环境数据阈值的设置对于移动机器人的避障规划有着至关重要的影响。环境阈值设置过大，机器人会丧失发现可行方向的机会;环境阈值设置过小，则会加大候选方向的面积，进而使移动机器人的航向角对于目标方向而言有较大的变化，这种变化不利于机器人运动控制的稳定性。对于前者，根据机器人的行进速度，本文设置机器人行驶速度大于800 mm/s时，机器人的航向阈值为2 500 mm/s，采样时间缩短为0．5 s;行进速度低于800 mm/s时，航向阈值为2 000 mm/s;

本文的机器人航向是取与目标点相关的2个障碍物之间的距离中线，如图8所示。

图8 可行空间角度的确定

根据算法计算，机器人为了避开障碍物，目标航向应该为π－θ/2角度。在这种情况下，转向角度将使机器人远离障碍物的同时，使得机器人的航向角变化过大，增加目标性运动的代价，不利于机器人的运动控制。故本文设置了如下转向角度限制:当行驶速度小于800 mm/s时，最大自由扇区极限设计为30°，即θ最大为30°;当行驶速度大于800 mm/s时，最大自由扇区极限设计为20°，即θ最大为20°。

根据上述方法，当机器人以900 mm/s行驶时，仿真实验结果如图9所示。验证了这样的设置既保障平台的安全航向方向，又减少了平台航向角的剧烈变化。

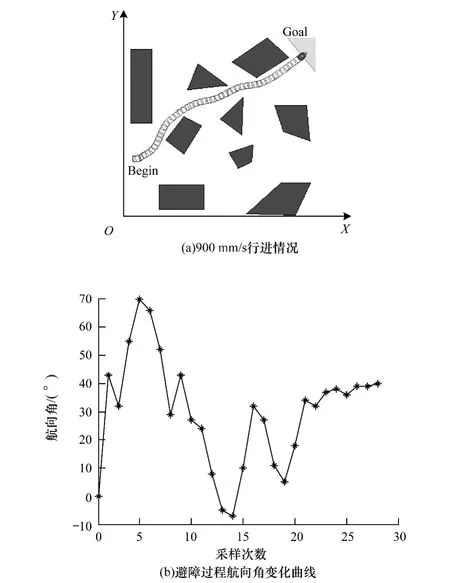
图9 900 mm/s行驶时的仿真实验结果

4 结束语

本文基于激光雷达传感器提出一种移动机器人新的避障方法，该方法具有计算量小、实时性高等优点，适用于移动机器人的实时避障规划。利用障碍物方向与目标方向之间的位置关系，确定算法的不同自由方向安全阈值;同时针对不同行进速度，通过设置最大航向角度，解决了阈值不足时，移动机器人出现的航向剧变问题。仿真结果表明，即使在复杂的障碍物环境中，该方法控制的机器人仍能够安全无碰撞地到达目的地。

［1］ Borestein J，Koren Y．The Vector Field Histogram-fast Obstacle AvoidanceforMobileRobots［J］．IEEE Transactions on Robotics and Automation，1991，7(3):278-288．

［2］ Borestein J，Koren Y．Real-time Obstacle Avoidance for Fast Mobile Robots［J］．IEEE Transactions on Systems，Man，andCybemetics，1989，19(5):1179-1187．

［3］ Ulrich I，Borenstein J．VFH +:Reliable Obstacle Avoidance for Fast Mobile Robots［C］//Proceedings of International Conference on Robotics ＆ Automation．Washington D．C．，USA:IEEE Press，1998．1572-1577．

［4］ Ulrich I，Borenstein J． VFH *:Local Obstacle Avoidance with Look-ahead Verification［C］//Proceedings of International Conference on Robotics＆Automation．Washington D．C．，USA:IEEE Press，2000:2505-2511．

［5］ 章苏书，吴 敏，曹卫华．一种局部动态环境下的避障算法［J］．计算机技术与自动化，2003，22(1):12-16．

［6］ 廖小翔，胡旭东，武传宇．基于高斯概率分布场的VFH避障算法的研究［J］．机械设计与研究，2005，21(1):31-34．

［7］ 许心德，关胜晓．未知环境下基于VFH*的机器人避障［J］．计算机仿真，2010，27(3):156-160．

［8］ Kazem B I，Hamad A H，Mozael M M．Modified Vector Field Histogram with a Neural Network Learning Model for Mobile Robot Path Planning and Obstacle Avoidance［J］．International Journal of Advancements in Computing Technology，2010，5(2):166-173．

［9］ Goh Wooi-Boon，Chan Kai-Yun．Part-based Shape Recognition Using Gradient Vector Field Histograms［C］//Proceedings of the 10th International Conferenceon ComputerAnalysisofImagesand Patterns．Berlin，Germany:Springer，2009:402-409．

［10］ 曹卫华，吴净斌，吴 敏，等．无路标环境下遥操作机器人 SLAM 系统［J］．智能系统学报，2010，5(3):240-246．

［11］ 徐 璐，陈阳舟，居鹤华．基于动态行为控制的移动机器人自主避障［J］．计算机工程，2007，33(14):180-182．

［12］ 徐玉华，张崇魏，徐海琴．基于激光测距仪的移动机器人避障新方法［J］．机器人，2010，32(2):179-183．