基于GPU的碳纳米管分子动力学并行仿真

孟小华，覃大胜，郑冬琴，周玉宇

(暨南大学 a．计算机科学系;b．物理系，广州510632)

1 概述

自从文献［1］首次应用分子动力学研究硬球系统以来，分子动力学广泛应用于晶体生长、压痕试验、摩擦学以及低压金刚石合成等领域。在新兴的纳米工程领域，建立在连续介质基础上的宏观机理很难解释纳米工程中出现的一些特殊现象，因而分子动力学方法成为重要的研究手段之一［2］。文献［3］通过分子动力学模拟了Ni针尖在Au(001)表面的纳米压痕过程，其模拟结果发表在《科学》上，成为该领域的标志性成果。文献［4］通过分子动力学仿真算法，研究了不同晶粒尺寸的多晶铜塑性变形过程，从而发现晶粒尺寸与强度不完全满足Hall-Petch关系。

分子动力学仿真算法，有着理论分析方法和实验方法无法比拟的优点，但是其计算要求极高，往往受限于计算机的计算能力。为了提高仿真算法规模，国内外许多专家学者做了大量研究［5-7］。仿真算法已由最初提高单机规模的串行算法［8］，发展到如今通过将计算任务分配给多个CPUs，从而提高模拟规模的并行算法［9］，规模也由最初的几千个原子提高到上百万、上千万甚至到上亿个原子。由于碳纳米管［10］系统中含有大量粒子，结构和受力复杂［11］，其分子动力学模拟需要极强的计算能力，对CPU处理能力也有较高的要求。而利用CPU实现仿真串行算法，计算量极大，运算时间长，并且模拟粒子数也受到很大的限制。

本文基于CUDA平台，通过调度GPU多个流处理单元［12-13］，利用GPU强大的并行计算能力和高效的数据传输能力，对碳纳米管分子动力学的并行仿真算法进行研究和实现，通过把碳纳米管系统分成多层可并行处理的单元进行并行计算。

2 分子动力学Verlet仿真算法

分子动力学是一套分子模拟方法，是一种重要且有效的原子尺度计算机模拟手段。该方法主要依靠牛顿力学来模拟分子体系的运动，以在由分子体系的不同状态构成的系统中抽取样本，从而计算体系的构型积分，并以构型积分的结果为基础进一步计算体系的热力学量和其他宏观性质。因而，用分子动力学是碳纳米管仿真的重要途径。

在分子动力学Verlet仿真算法中，粒子位置的泰勒展开式如下:

(1)将x(t+Δt)和x(t－Δt)进行泰勒展开如下式所示:

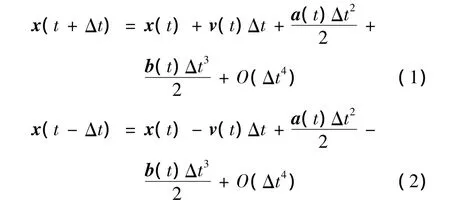
其中，x(t－Δt)表示为前一时刻的位置;x(t+Δt)表示为后一时刻的位置。

(2)将式(1)和式(2)相加，得到位置表达式如下:

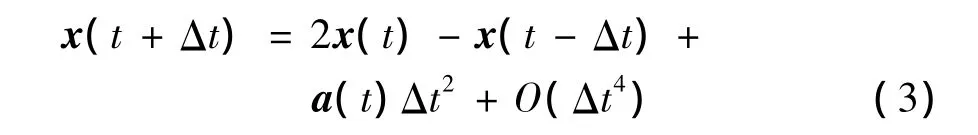
(3)将式(1)和式(2)相减，再两边同时除以2Δt，获得速度的表达式如下:

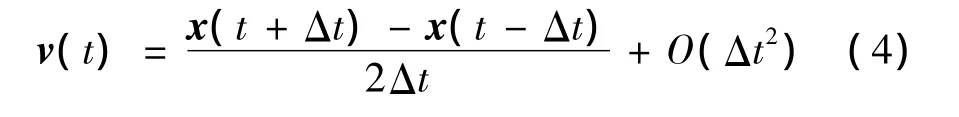
(4)由式(1)～式(4)，在已知粒子 t－2Δt时刻的位置 x(t－2Δt)、t－Δt时刻的位置 x(t－Δt)和t－Δt时刻的加速度a(t－Δt)的情况下，启动Verlet算法进行积分:根据 x(t－2Δt)，x(t－Δt)和 a(t－Δt)，将 t=t－Δt代入式(3)，获得 x(t);根据 x(t)，基于一定的势函数更新a(t);同时，根据x(t)和x(t－2Δt)，将t=t－Δt代入式(4)，更新v(t－Δt);即得到粒子x(t)，v(t－Δt)和a(t)，重复执行该步骤。

由上，可利用Verlet列表法设计串行仿真算法的实现步骤如下:

(1)先构造如图1所示的碳纳米管结构模型，并设置各种参值。

(2)设计前端热浴和后端热浴。

(3)构造并调用计算碳纳米管结构内部的力的结构函数及计算碳纳米球C60与碳纳米管间范德华力的函数等。

(4)计算所有的力，解牛顿运动方程，分层计算并积分(算法的核心)。

(5)模拟出碳纳米球C60随着热浴时间的运行轨迹，根据运算结果，可画出和碳纳米管内随着能量传送的温度变化曲线图。

3 基于CUDA并行仿真算法的研究与实现

3．1 碳纳米管系统模型的建立

在数据库文件中读取碳纳米管系统的参数条件，如初始温度、粒子数、密度时间等，构造碳纳米管系统模型MOD1及参数模型MOD2，模型MOD2可以设置各种参数在模型MOD1上使用，模型MOD1如图1～图3所示，由碳纳米管和设置在碳纳米管内部的一个足球状C60分子(由60个碳原子构成的分子，形似足球，又名足球烯)组成，所述碳纳米管为层状中空结构，管身是准圆管结构，由多个六边形碳环结构单元组成，其直径一般在一到几十个纳米之间，长度则远远大于其直径，对该模型进行初始化，读取模型中所有粒子的速度和位置坐标。

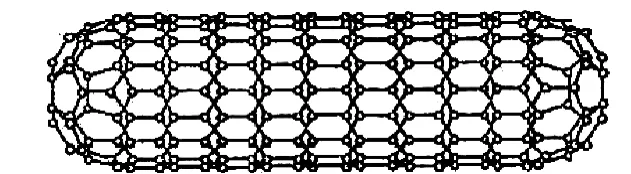
图1 碳纳米管

图2 C60分子

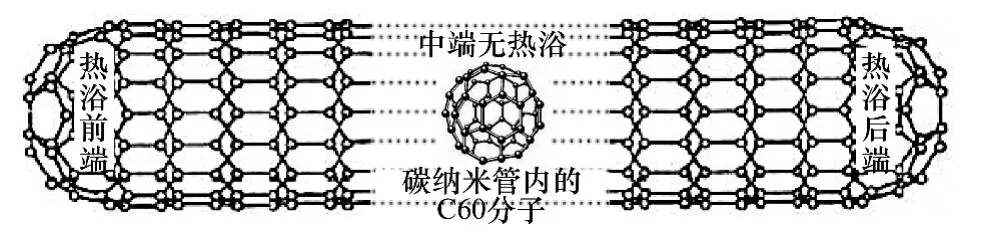
图3 碳纳米管系统模型

在碳纳米管中，除管口层粒子外，其余粒子相互组成正六边形。如图4所示，非管口粒子都有3个近邻粒子(ip，jp，kp均为idx粒子的近邻粒子)。

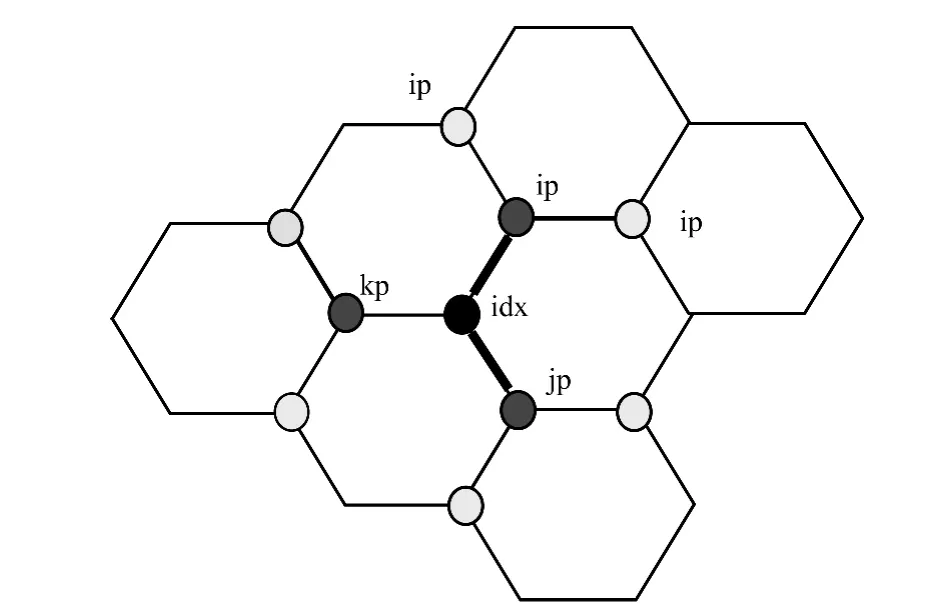
图4 碳纳米结构

在碳纳米管系统中，因为C60分子受到碳纳米管管壁上碳粒子产生的力，在平衡位置上来回振动，当C60分子处于平衡状态时，采用Gaussian热浴法(约束温度调节方法)，在碳纳米管两端同时分别设置不同温度的热浴条件，并设定热浴时间，使碳纳米管管壁上碳粒子和C60分子因平衡状态被打破而发生位置和速度的变化。而这些变化是相互影响的，具有传递性，伴随着这些粒子位置和速度的变化，能量在长管状的碳纳米管系统内发生传递。由于C60分子位于碳纳米管内，其受力会随着碳纳米管组成粒子的位置改变而改变，因此伴随着能量传递的过程，C60分子的运动状态和能量也会发生改变;采用Gaussian热浴法的基本原理是在运动方程中加入摩擦力fi，并将其与粒子速度vi联系起来，其受力公式为:

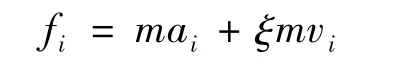
当平衡态时，系统温度不变，因此有dEk/dt=0。即有:，由此可得

3．2 并行仿真算法研究

在CUDA平台上对碳纳米管进行分割，分割成多层大小适宜、相互独立的计算单元，分割原则是在避免过多重复计算的前提上提高并行度，即分割的计算单元必须合理粗细化。因为计算单元过大，则并行不明显，计算单元过小，会导致太多不必要的重复计算。由于粒子间的作用力间距影响较大，必须设定一个距离临界值，以判断其位置关系，当粒子间的间距小于距离临界值，为近邻粒子;当粒子间的间距大于距离临界值，为次邻粒子，则认为其相互间的分子作用力可以忽略不计。

可以预料到的是每个中心粒子最多只会对其3个近邻及3个近邻的各2个近邻，即6个次邻施力。可以这样来考虑，以中心粒子以及3个近邻6个次邻划分到一组计算。分批次并行计算。在某一批次计算中，未当成中心粒子计算的一个粒子加入可并行计算队列中，由于竞争关系，其3个近邻6个次邻在本批次中将不能加入队列，同样的，对这3个近邻6个次邻施力的其他所有未计算粒子也不能加入队列中。这样，同一批次的粒子将可以并行计算而不产生竞争关系。

设计分裂算法，采用CPU遍历计算单元得到n个可并行运算队列:

(1)若所有粒子均已作为中心计算粒子，跳到步骤(8)。

(2)按次序找到第一个非竞争粒子并没有按中心计算的粒子，加入可并行运算队列。

(3)标记该粒子的所有近邻为本并行队列一度不可并行粒子，若近邻已经是二度不可并行粒子，则提升为一度不可计算。

(4)标记该粒子所有次邻为本并行队列二度不可并行粒子，若次邻为一度不可并行粒子，则不修改其度数。

(5)标记本粒子为已按中心计算粒子。

(6)判断是否已遍历到粒子队尾。若是继续执行，若否跳到步骤(1)。

(7)下一个可并行队列开始，返回步骤(2)。

(8)结束。

分裂算法在CPU预处理阶段完成，只计算一次得出的可并行队列可以在后面的循环计算中一直使用。当循环次数较多时，分裂算法所使用的时间占总时间比例将大大减少，对程序总体性能影响也降到比较低的程度。但是由于算法核心是批次计算，因此计算力时将多次启动内核计算函数，一定程度上加大了运行开销。

如图5和图6所示，调度GPU的流处理单元，采用Verlet算法进行并行运算和处理:

(1)按碳纳米管系统模型所有粒子的位置，计算近邻粒子以及次邻粒子间的键关系和角度关系。

(2)调度GPU的流处理单元，并行计算被分割在不同计算单元里的粒子，并积累计算碳纳米管管壁上每个粒子与其近邻粒子的相互作用力。

(3)根据C60分子所在区域，计算C60分子内每个粒子与其所在碳纳米管区域中的每个粒子的相互作用力(范德华力)。

(4)根据粒子所受到的力及其速度，更新粒子位置，再执行步骤(2)和步骤(3)。

(5)根据粒子所受到的力，计算粒子本次速度及碳纳米管前、后两端热浴的热流值。

(6)若达到循环频数，则计算结束;否则，在CPU端间隔保存粒子的数据，返回步骤(4)。

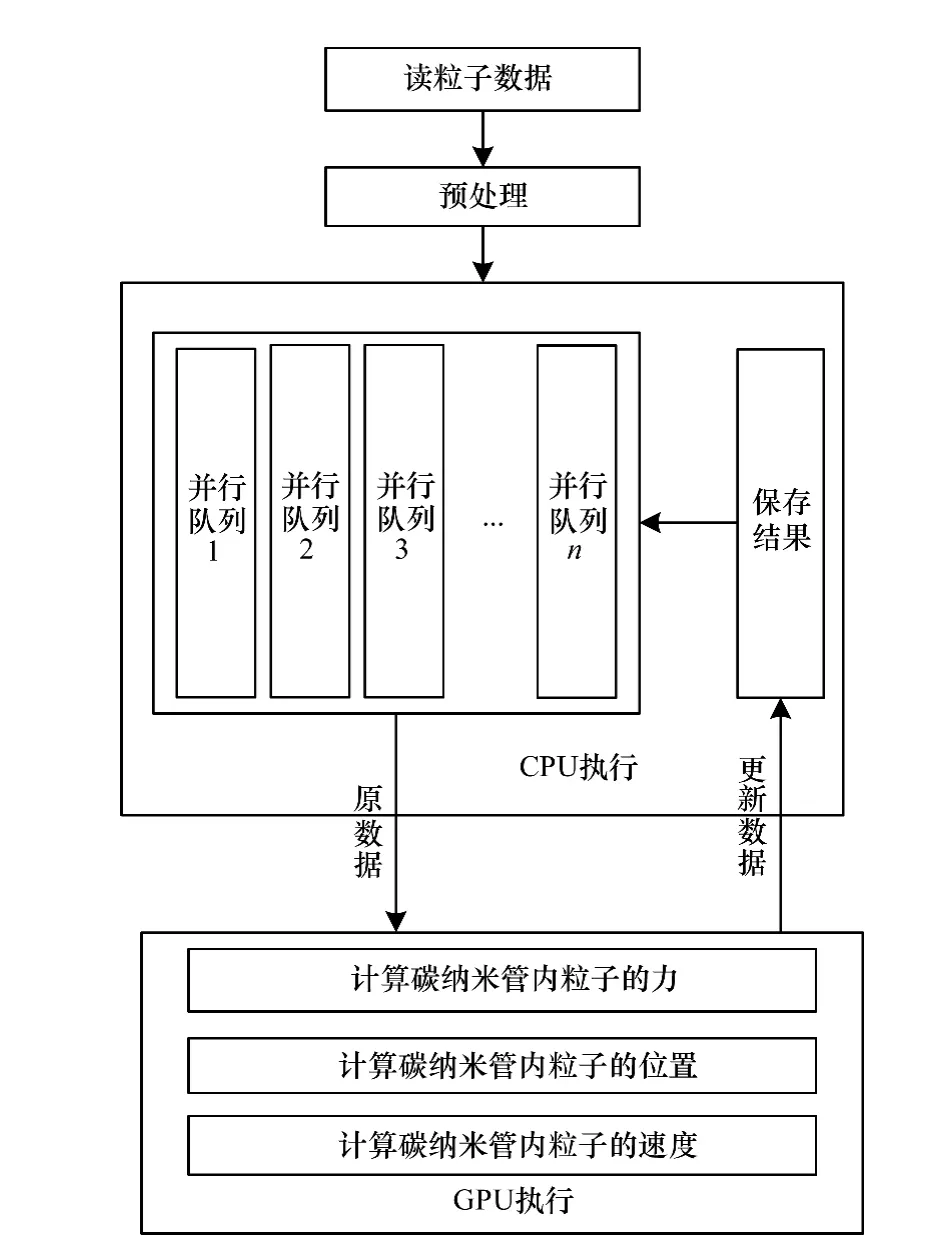
图5 碳纳米管分子动力学并行仿真中的调度模式

图6 碳纳米管分子动力学并行仿真算法的流程

4 GPU并行算法的优化

Verlet仿真程序是一个计算力→计算位置→计算速度→计算力……的不断循环过程，每个粒子独立运行一个线程，然后循环成千上万次甚至更多，因此小部分的程序优化也会给整个程序带来极大的性能提升。对于CUDA的程序而言，优化主要集中在指令优化、存储器访问优化、网格优化以及资源均衡等。

4．1 指令优化

目前，GPU单精度计算性能要远远超过双精度计算性能，因此，程序中对精度要求不高的部分可使用单精度运算代替双精度运算。在GPU中整数乘法、除法、求模运算的指令吞吐量较为有限，而控制流指令由于会影响指令发射器的并行发射，打断指令流开销巨大。此时，在可知整数范围中以经优化的库24位整数运算__mul24，__umul24代替32位整数运算，以__sinf(x)，__fdivide(x，y)等代替相应的运算。尽量避免整数除和模运算，或以(i＆(n－1))代替(i%n)，除数是2的幂次方时以移位运算代替除法。

4．2 存储器访问优化

合理使用share memory资源，减少不必要的临时变量，使用精简函数以减少register使用。同时，将程序中的常量以及计算中可合并常量保存于constant memory常量存储器中。Global memory是显存中容量最大的存储器，可被任意GPU线程读写存储器任意位置，但由于全局存储器没有缓存，具有较高的访存延迟。因此，程序中在减少不必要全局存储读写的同时，增加处理器占用率，即当一个block访存时，另一个block可切入运算隐藏延迟。此外，改变显存的存储结构，尽量满足合并访问存储器。

4．3 CPU+GPU 处理

考虑到GPU并行处理要发挥其强大的并行计算能力，要有足够多的线程并行运算。因此，把部分较小计算量的计算交给CPU执行。如计算C60与炭纳米管间范德华力函数，由于C60只有60个粒子，相对来说并行度小，将其计算放到CPU里。由于内核的启动是异步的，因此把CPU函数放到内核启动函数下面，CPU启动内核执行GPU运算时可立即返回执行CPU程序，实现CPU与GPU的并行处理。

5 实验结果与分析

本文测试在 Widows 7平台下进行，GPU1和GPU2是2个不同型号的显卡，每次实验只选取其中一块显卡。为准备记录运行时间并方便CPU与GPU并行运行，测试时间以CPU时间为记录。部分硬件参数如表1所示。

表1 测试平台部分硬件参数

分别使用CPU串行、GeForce GT 430显卡和Quadro 2000显卡按不同粒子数计算，测试三者耗时，如表2所示。

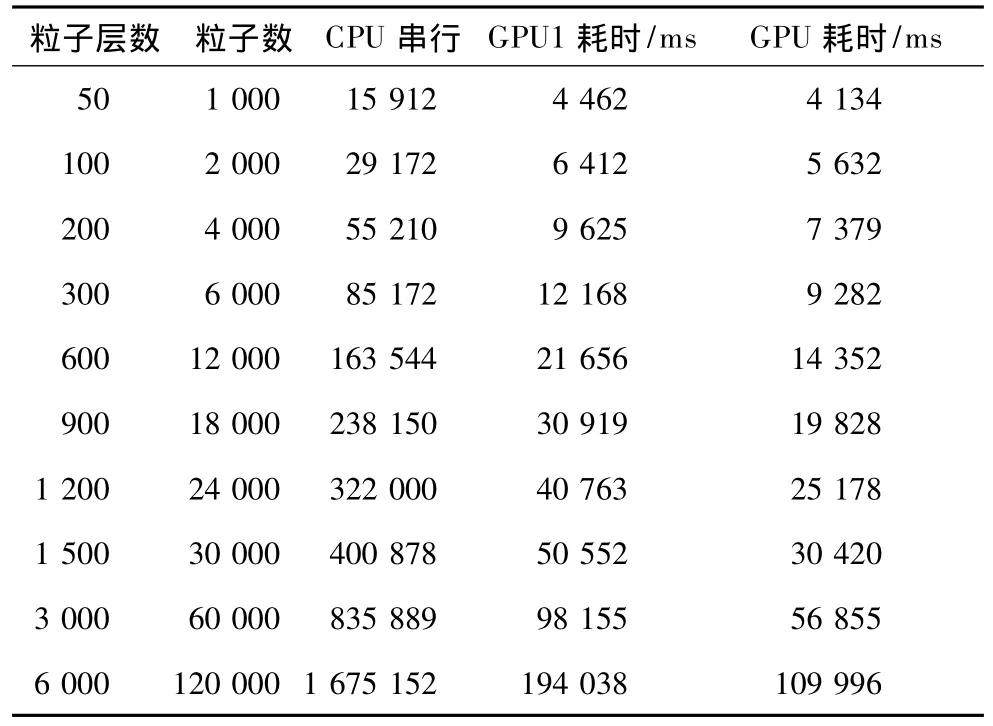
表2 串行并行程序运行于不同硬件平台时的数据

5．1 不同GPU间并行算法性能对比

为使数据形象化，将GPU1与GPU2数据绘制成条状图。由图7可得，前期粒子数较少时，2种显卡耗时相差不大，但随着粒子数的增加，GeForce GT 430显卡耗时增长速度逐渐快于Quadro 2 000显卡。而当粒子数量增加到120 000个时，前者耗时几乎是后者的2倍。

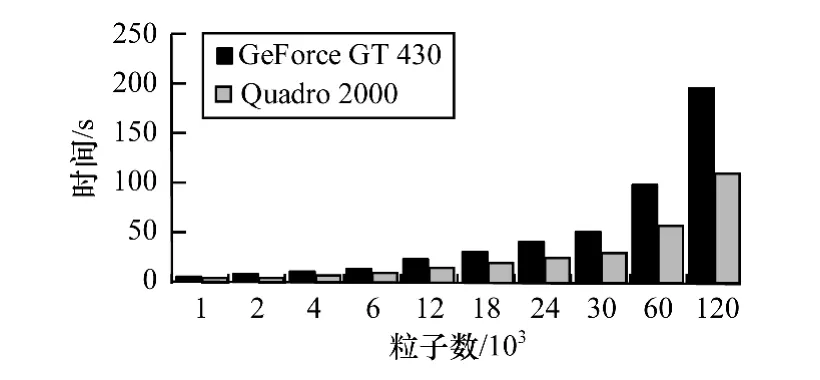
图7 2种并行显卡运行程序耗时对比

由表1可知，Quadro 2 000有着2倍于GeForce GT 430的 CUDA Cores(即流处理器 stream processor)。结合GPU的线程运行方式，当GPU的处理单元增多，同时处于运行状态的线程也会相应增加。因此，当无其他硬件限制时，GPU并行计算的性能几乎随着GPU处理器的增加而线性增加，使用拥有更多处理器的GPU能给Verlet带来更多的性能提升。

5．2 串并行算法性能对比

对比CPU串行程序与GPU并行程序的性能，计算不同粒子数下耗时，GPU使用Quadro 2000。

表格数据绘制成串并行程序执行时间对比如图8所示。可以明显看出，当要计算的粒子数不断增加时，并行程序相比于串行程序的加速比有一定程度的增加。粒子数量在1 000～4 000时，由于线程数据不足，不能很好地隐藏GPU程序加载时间、数据传输时间以及访存时间。当粒子数量不断增加时，加速效果越来越好。

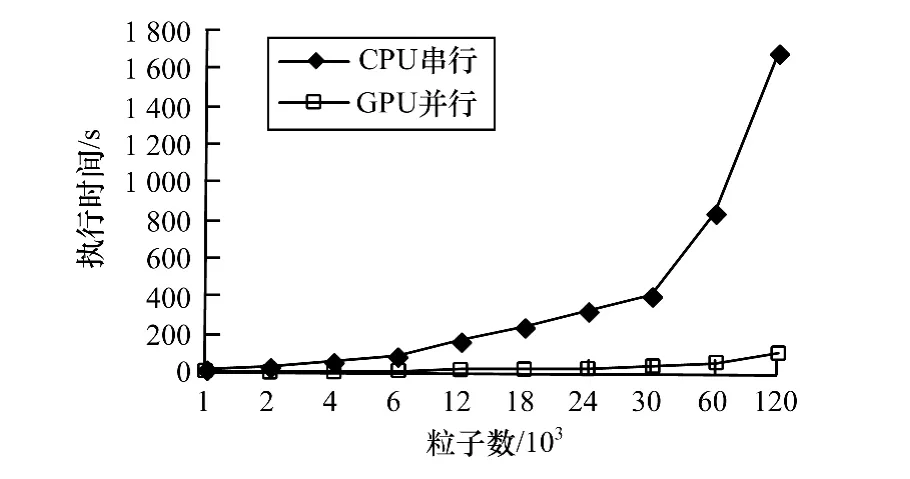
图8 串并行程序执行时间对比

5．3 并行算法性能分析

为分析并行算法的加速比，将表2中串并行程序运算时间按公式:

计算，GPU使用Quadro 2000，并将结果绘制成GPU并行计算加速比，如图9所示。

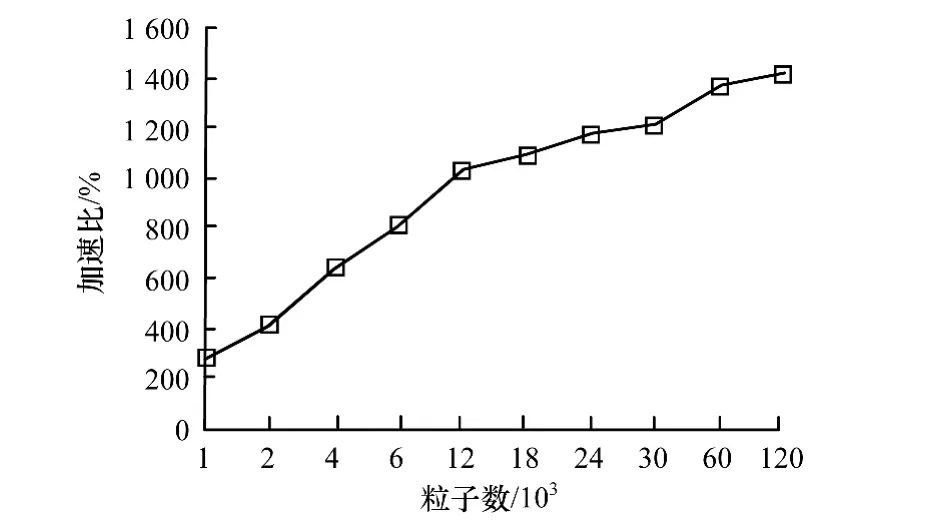
图9 GPU并行计算加速比

可以看出，随着粒子数的增加，GPU并行算法相比于串行算法的加速比也随之增大。当粒子数到达120 000个时，加速比达到1 400%，即14倍的加速效果。

为分析影响GPU并行程序性能因素，使用性能评估工具NVIDIA Visual Profiler对程序进行分析。目标程序计算600层12 000个粒子，每个block中有128个线程。首先分析各函数运行时间占总运算时间的比例。通过多次运算求平均值，如图10所示。

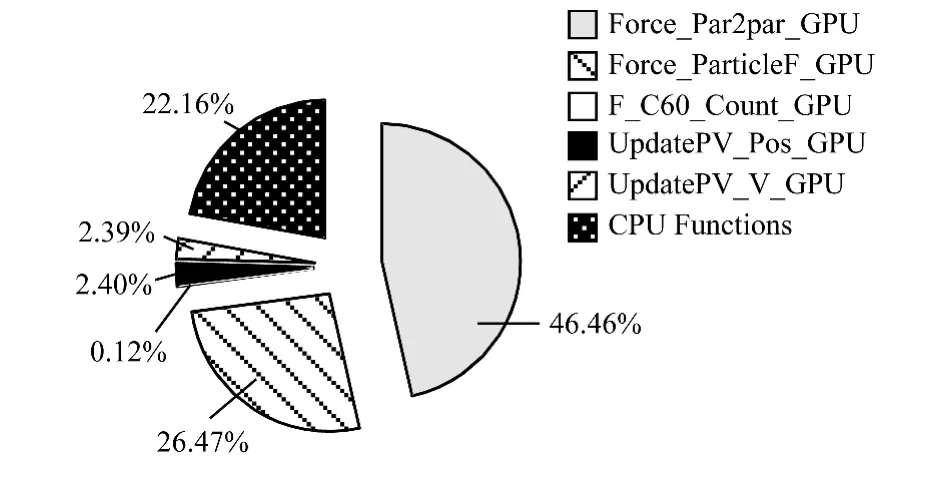
图10 各个函数的比重

6 结束语

在对碳纳米管分子动力学进行仿真时，原来的分子动力学仿真算法有良好的效果，但因碳纳米管系统粒子数的规模太大、计算量多、运行时间长，缺乏实用性。而由用Verlet算法实现的分子动力学仿真算法具有易并行性，可以在具有强大图像处理和浮点计算能力的GPU上并行处理，从而大大提高了碳纳米管分子动力学仿真算法的效率。

实验结果表明，对小规模仅有120 000个粒子组成的碳纳米管系统，在拥有192个流处理器的NVIDIA Quadro 2000显卡上实现的GPU并行仿真算法，与在拥有4核8线程的Intel Xeon W3550上实现的基于CPU的串行仿真算法相比，其加速比即可达到十多倍，从而有效地解决了算法速度上的缺陷。

然而由于本次实验的硬件条件有限，所能计算的碳纳米管系统规模有限，因此无法深度发掘CUDA的能力。而由实验结果所示，碳纳米管系统的粒子数规模越大，GPU并行算法对于串行算法的加速比就越明显。在实际运用中，碳纳米管系统的粒子数的规模都很大，超过千万乃至十亿，可以预估该基于GPU的分子动力学并行仿真算法，对碳纳米管的研究会发挥至关重要的作用。

［1］ Alder B J，Wainwright T E．Phase Transition for a Hard Sphere System［J］．The Journal of Chemical Physics，1957，27(5):1208-1209．

［2］ 唐玉兰，胡 适，王东旭，等．纳米工程中大规模分子动力学仿真算法的研究进展［J］．机械工程学报，2008，44(2):8-15．

［3］ Landman U，Luedtke W D，Burnham N，et al．Atomistic Mechanisms and Dynamics of Adhesion，Nanoindentation，and Fracture［J］．Science，1990，248(4954):454-461．

［4］ Schiøtz J，Jacobsen K W．A Maximum in the Strength of Nanocrystalline Copper［J］．Science，2003，301(5638):1357-1359．

［5］ 徐 伟，王 丽．MD算法在集群系统中的并行实现研究［J］．计算机工程，2002，28(3):103-105．

［6］ Proctor A J，Lipscomb T J，Zou Anqi，et al．Performance Analyses of a Parallel Verlet Neighbor List Algorithm for GPU-optimized MD Simulations［C］//Proceedings of International Conference on Biomedical Computing．Washington D．C．，USA:IEEE Press，2012:14-19．

［7］ Anderson J A，Lorenz C D，TravessetA．General Purpose Molecular Dynamics Simulations Fully Implemented on Graphics Processing Units［J］．Journal of Computational Physics，2008，227(10):5342-5359．

［8］ Verlet L．Computer Experiments on Classical Fluids．I．Thermodynamical Properties of Lennard-Jones Molecules［J］．Physical review，1967，159(1):98-103．

［9］ Tamayo P，MesirovJP，BoghosianB M．Parallel Approaches to ShortRange Molecular Dynamics Simulations［C］//Proceedings of Conference on Supercomputing．New York，USA:ACM Press，1991:462-470．

［10］ 曹 伟，宋雪梅，王 波，等．碳纳米管的研究进展［J］．材料导报，2007，21(5):77-82．

［11］ 刘文志，李晓霞，余 翔，等．分子动力学模拟中基于GPU的范德华非键作用计算［J］．计算机与应用化学，2010，27(12):1607-1612．

［12］ 孟小华，刘坚强，区业祥，等．基于CUDA的拉普拉斯边缘检测算法［J］．计算机工程，2012，38(18):190-193．

［13］ 孟小华，黄丛珊，朱丽莎．基于CUDA的热传导GPU并行算法研究［J］．计算机工程，2014，40(5):41-44，48．