基于改进k-medoids算法的XML文档聚类

2015-01-02冯少荣潘炜炜林子雨

计算机工程 2015年9期

冯少荣，潘炜炜，林子雨

(厦门大学信息科学与技术学院，福建厦门361005)

1 概述

XML由于其具有通用性、可扩展性、易用性、自描述性、异构性和开发性等特点［1-2］，已成为Web上通用的数据表示和交换格式。随着XML文档数量呈现出爆炸式的增长，人们迫切地需要从这些文档中获取相应的信息知识。XML文档的自动聚类，不仅可以增强网络中XML文档的组织性，同时还能从海量的XML文档中发现未知、隐含的知识和文档间的联系［3-5］，具有重要的研究意义。由于XML文档除了一些文本内容之外，还具有元素父亲节点、子孙节点嵌套等结构特征，因此传统文档聚类算法并不适合于XML文档的聚类。目前对XML文档的聚类，主要有 k-means(均值)［6］和 k-medoids(中心点)［7］2种基于划分的方法。由于XML文档数据集包含一个个离散的对象，而k-means的均值并不能真正反映整个簇的实际情况，也没有实际的意义。同时k-means算法对孤立点十分敏感，相比之下，kmedoids采用某一个具体对象作为聚类中心，很好地解决了k-means对孤立点敏感这一问题。同时，k-medoids算法具有划分简单、执行时间快的特点，其操作也适合于XML文档聚类。因此，k-medoids在XML文档聚类中得到了广泛的应用。

在基于划分的文档聚类中，一个最基本的问题是要确定聚类的个数k。这样对算法的使用造成了很大的不便，且无法通过样本的特征自动地确定聚类个数。此外，基于划分的聚类、初始中心点或者质心的选择，对整个聚类过程和聚类结果也有较大的影响，不合理的初始中心点选择容易使得算法得出局部最优解。针对以上2个问题，本文运用模糊聚类和遗传算法(Genetic Algorithm，GA)来确定聚类个数和最佳初始聚类中心，并在此基础上结合k-medoids算法实现对XML文档的聚类。

2 XML文档相似度计算

XML文档的结构是一个树状的模型，XML中既包含结构信息，也包含语义内容信息，以往的研究主要围绕这2个方面展开。但文献［8］证明语义内容信息在XML文档相似性度量中作用不大，并且由于不断查询WordNet词典，导致算法计算开销增加。因此，本文主要基于结构来度量XML文档相似性。

多数对XML文档的操作都是映射成XML文档树再进行相关运算。文献［9-11］提出了基于编辑距离的方法计算文档的相似度。这种方法的缺点是复杂度过高，不利于实际的应用。文献［12］提出了基于树-路径的模型，相对于编辑距离的方法复杂度较小。但是这种方法在匹配2棵文档树路径时用的是路径全匹配的策略，这样的结果会丢失一部分的相似信息，导致相似度的计算有所偏差。本文基于文献［13］公共子路径相似度的计算方法，实现文档相似度的计算。

定义1子序列及公共子序列

称序列＜ai1，ai2，…，aik＞为另一个序列＜a1，a2，…，an＞的子序列，当且仅当1≤i1＜i2＜… ＜ik≤n;称序列＜ a1，a2，…，an＞和＜ b1，b2，…，bm＞的公共子序列为＜c1，c2，…，ck＞，当且仅当＜c1，c2，…，ck＞既是＜a1，a2，…，an＞的子序列，又是＜ b1，b2，…，bm＞的子序列。

在计算路径相似度时，本文引入位置权重向量w=(w(1)，w(2)，…，w(n))，其中，1，2，…，n 为公共子序列的下标。加入位置权重的意义在于，一个相同的节点位置越靠前，其贡献的信息量越大，越是重要，所以位置权重向量满足:当i＞j，w(i)＞w(j)。

定义2路径相似度

设通过路径 P1=(f1，x1，x2，…，xn)和 P2=(f2，y1，y2，…，ym)求得的最长公共子序列为 P=(a1，a2，…，ak)，其中，k 为 P1和 P2最长公共子序列的长度。记P中节点在P1中的位置下标为(l1，l2，…，lk)，记P中节点在 P2中的位置下标为(h1，h2，…，hk)。由此可得P1和P2的路径相似度S计算公式为:

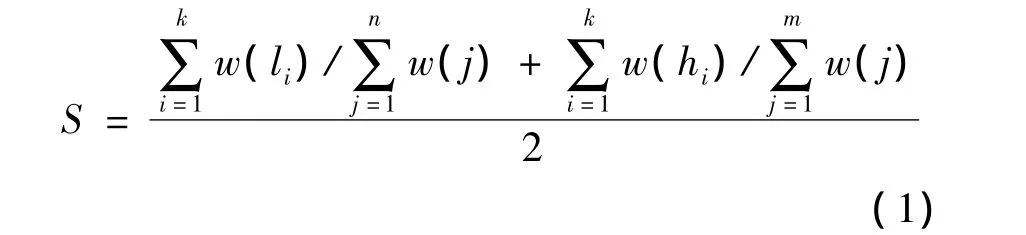
根据路径相似度可以得出文档相似度的计算方法。设2个文档D1和D2，通过计算2个文档之间的每条路径所能达到的最大的相似度值S，得到文档相似度Sim的计算公式为:

根据所得到的文档相似度公式，计算2个文档的相似度的算法伪代码如下:

输入 2棵文档树Doc1，Doc2

输出 2个文档的相似度Sim

计算2个文档的相似度的计算量，复杂度由以下关键处理过程决定:

(1)2个文档各自所包含的路径数量乘积决定了获得最长公共子序列和式(1)的执行次数;

(2)2个文档各自所包含的路径数量决定了式(2)的计算量和复杂度。

该算法具有2个显著特点:(1)采用最长公共子序列来匹配2条路径，使得路径的相似信息的获取更完备;(2)在路径相似度的计算中引入了位置权重，使得相似度计算更合理，接近实际。

3 XML文档聚类的有效性指标

一个紧致的、良性划分的聚类应当使聚类中心的间距尽可能大，而XML文档样本与其中心间距尽可能小假设对于数据集 D={x1，x2，…，xn}，最终聚类个数为 k，则聚类结果可表示为(D1，D2，…，Dk)，聚类的中心点表示为(p1，p2，…，pk)。这种划分的结果可以表示为一个 k×n阶矩阵 U=(uij)k×n，uij∈［0，1］，对任意的。对任意的因此，可以根据这个特征定义XML文档聚类的有效性指标Q如下:

其中，Q值越小，则其聚类质量越好。

4 k-medoids算法聚类个数的确定

利用k-medoids算法进行XML文档聚类，聚类个数的确定是一个关键的问题。确定聚类个数过程的性能最终取决于所应用的聚类算法。另一方面，由于一般文档聚类方法并不能很好地适应XML文档聚类。本文基于这两点，提出了一种快速有效的基于模糊聚类的方法，能够很好地确定聚类个数。

基于模糊等价关系的聚类方法，能够简单地通过对模糊相似矩阵的λ截运算，快速地产生一个聚类结果。本文利用XML文档聚类必须先得出相似度矩阵的这一必要过程，通过模糊等价矩阵的方法，快速得到不同λ阈值下的聚类个数，最终用聚类有效性指标作为评估函数，确定最佳的聚类个数。

由于相似度取值在［0，1］内，显而易见，λ也落在这个区间中。可以遍历［0，1］区间来获取不同的λ值，进行基于模糊等价关系的聚类。但需要确定λ在［0，1］之间如何取值。本文根据相似矩阵内部不同取值之间的差值大小，动态决定λ值大小。

定义3 设d为λ在［0，1］间取值的间隔值，且(s1，s2，…，sn)为相似度矩阵中的相似度值从小到大的排列序列，即满足s1≤s2≤…≤sn，由此得到d的计算公式为:

因此，可以得到基于模糊等价关系确定聚类个数的算法如下:

输入 XML文档数据集的相似度矩阵Rsim

输出最佳聚类个数k

确定聚类个数的计算量，复杂度由以下关键处理过程决定:

(1)获得样本集的模糊相似度矩阵;

(2)通过“平方法”把模糊相似矩阵改造成模糊等价矩阵;

(3)根据式(4)计算出阈值d;

(4)根据计算得到的阈值d，利用不同的λ取值下的截矩阵，进行模糊等价关系的聚类;

(5)利用评价指标函数，计算每次聚类结果的评价值，并记录评价值最高的聚类结果的聚类个数。

因此，确定聚类个数的计算复杂度为O(tequal_sim+n×tvalue)，其中，tequal_sim为获得模糊等价矩阵及计算阈值所花费的时间;n为根据阈值划分［0，1］区间的个数;tvalue为根据聚类有效性指标计算聚类评价值所花费的时间。

5 k-medoids最佳初始聚类中心点的确定

对于初始中心点的选择问题，本文引入了遗传算法，通过遗传算法所具有的全局最优解的搜索能力，改善确定最佳初始中心点这一步骤，使得在遗传算法的个体迭代过程中，逐步把聚类的中心点向实际的聚类中心点靠拢，最后达到获得最优解的目的。遗传算法与k-medoids结合的算法已有研究者提出类似的想法［14-15］，虽然其算法对一般的聚类问题具有普遍适应性，但是针对XML文档的聚类会存在一些问题。为此，本文提出了针对XML文档聚类的相关特征的适合XMIL文档聚类的遗传算法。

5．1 遗传算法的操作过程

5．1．1 编码策略

本文所采用的编码方式是实数编码，结合XML文档聚类的特点以及结合k-medoids算法，提出了以初始聚类中心为基因位而形成的编码方式。

设数据样本集D中XML文档的个数为N，染色体基因位a的取值范围为［1，N］。这样设定的好处在于，每个基因位既可以对应样本集D中位置，同时也和相似度矩阵中该对象的行列坐标一一对应，使得之后的其他遗传算子操作十分方便。假定聚类个数为 k，随机初始化的聚类中心点为(a1，a2，…，ak)，其中，当 i＜j，ai＜aj;当 i≠j，ai≠aj。于是一个具有 k 长度的个体的染色体可形式化为［a1a2…ak］。从编码方式来看，一条染色体代表的含义是以这些基因位为聚类中心点的一次聚类结果。在运用k-medoids算法的过程中，相同的初始化中心点，最后所得到的聚类结果是唯一的。因此，一条染色体编码和一次聚类结果是唯一确定的关系。

5．1．2 种群的初始化

本文希望初始化的解能在样本解空间中均匀采样，所以，在N个样本数据集的聚类中，随机生成2N个初始个体，然后选择较优的N个个体作为初始种群。

5．1．3 遗传操作算子的实现

本文采用的选择算子通过适应值比例选择，其中每个个体被选择的期望值为其适应值和群体的平均适应值的比值，该选择算子使用轮盘赌方式实现。采用的交叉方式是一致交叉。至于变异算子，由于变异概率的取值都很小，因此染色体有时候根本就不发生变异，这样导致浪费大量的计算资源。针对这种情况，一般采取如下变通的方法:

(1)计算个体发生变异的概率

以原始的变异概率pm为基础，可以计算出群体中个体发生变异的概率:

给定均匀随机变量 x∈［0，1］，如果 x≤pm(aj)，则对个体进行变异;否则不发生变异。

(2)计算发生变异的个体上基因变异的概率

由于发生变异的操作方式发生了改变，被选择变异的个体上的基因发生变异的概率也应该相应的进行改变，以保证整个群体上基因发生变异的期望次数相同。传统变异方式下整个群体基因变异的期望次数为n×k×pm。设基因变异的概率为下整个种群发生变异的期望次数为(n×pm(aj))×(k×)，且要求两者相等，于是满足:n×k×pm=(n×pm(aj))×(k×)，经过变换可得出的计算公式为:

由于编码方式采取实数编码，染色体中的每一位基因代表的是一个聚类中心点，因此当某一位变异时，其实际操作是在整个样本对象集合里面，通过随机得到一个对象，替代原来聚类中心点，从而形成新的变异后的染色体。例如，若染色体［1 12 23 34］的第2个基因位发生变异，而在规模为100的样本集里面随机获得的数据对象是60，则变异后得到的新染色体为［1 60 23 34］。

5．1．4 终止循环条件

终止循环的方法一般有如下3种:

(1)设置最大的遗传代数，该方法简单易行，但不准确;

(2)通过群体的收敛程度来判断，通过计算种群中基因的多样性测度来进行控制;

(3)根据每代的最佳个体的适应值变化情况来进行判定。

本文采取的方法是设置最大遗传代数的同时，也观察每一代中最佳个体的适应值情况，如果经过多次迭代后最佳个体的适应值基本不发生变化，则认为遗传算法已经收敛。

5．1．5 参数控制

在遗传算法的运行过程中存在着对其性能产生很大影响的一组参数，这组参数在算法的初始阶段就应该被合理地设定和选择，使得遗传算法的搜索轨迹能达到最优解。针对XML文档聚类问题，主要影响参数包括:群体规模n，交叉概率pc，变异概率pm。对这几个参数的具体选择将在实验部分展开讨论。

6 基于GA与k-medoids的XML文档聚类

经过上文讨论与分析，整个XML文档聚类的处理过程如下:

(1)输入XML文档样本数据集，计算得到相似度矩阵。

(2)通过基于模糊等价关系的聚类方法对相似度矩阵进行操作，得到最佳聚类个数。

(3)根据得到的聚类个数对个体进行编码，并初始化种群，每个个体编码对应一组随机选择的初始聚类中心点。

(4)对种群进行选择、交叉、变异操作，直到满足终止条件。

(5)在每次的遗传操作中，通过对个体的染色体基因进行处理，形成一组聚类中心点作为 kmedoids算法的初始中心点，并执行k-medoids算法进行迭代，直到算法结束，输出聚类结果。以聚类有效性指标作为适应度函数对聚类结果进行评价，其评价值就是该个体的适应度值。

(6)遗传迭代结束后，输出最优的个体，即最佳的聚类结果。

7 实验与结果分析

本文的XML文档实验数据来自于Niagara(http://www．cs．wisc．edu/niagara/data)和 sigmod(http://www．sigmod．org/record)中的任意抽取的10 个类别，包括了 bin，CUSTERM，actor，bib，movies，NATION，PART，personal，sigrecord 和SigmodRecord共计500个XML文档。为了测试本文算法的有效性，从这些数据集中随意抽取不同个数和类别的XML文档组成多个实验数据集合，进行相应的实验验证。实验使用DOM(Document Object Model)解析 XML文件，编程语言选用Java，并在Eclipse上实现。实验的平台是2．30 GHz i5-4200U处理器Windows 7操作系统。实验具体数据集如表1所示。

表1 实验数据集

7．1 聚类个数的确定

本文对XML文档聚类过程中的聚类个数的确定，采取了基于模糊等价矩阵的模糊聚类方法。为了测试算法的有效性，从整个数据集合中抽取多个类别的不同数量的XML文档进行多次实验，并同时记录了其时间效率，结果如表2所示。从表中可以看出，运用基于模糊等价矩阵的聚类方法所得出的聚类个数都与实际的聚类个数相同，证明此方法在确定XML聚类个数方面有效准确。此外，本文在D4和D5中还特别加入了孤立点数据，以验证孤立点对本算法在最后聚类个数的影响，结果表明此方法对孤立点不敏感。

关于算法的时间性能，分别选取了30个数据、80个数据、120个数据、200个数据和300个数据规模的样本进行实验，从表2中可以看出，算法的执行时间是线性增长的。最后，利用当前得到的数据，进行简单的线性回归，得到当数据量是3 000规模时，所需要的时间是3 422 ms，即3．4 s。综上可以得到，本文所提出的利用基于模糊等价矩阵的方法进行聚类个数的确定，不仅能得到与实际情况相符的聚类数目，而且在大规模数据集的应用上，算法的执行效率也是可接受的。

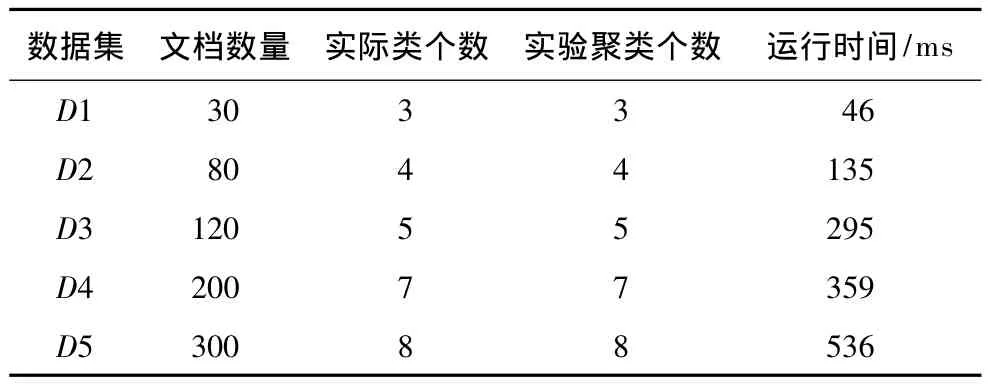
表2 聚类个数实验结果

7．2 遗传算法的参数控制

为了验证遗传算法与k-medoids结合的新算法对聚类的有效性，本文用准确率(precision)、召回率(recall)和F度量(F-measure)进行评估，另外，还加入有效性指标Q作为评判标准。通过上述4个指标可以综合评估聚类结果的好坏。

在遗传算法的运行过程中，存在着对算法性能产生影响的一组重要参数，包括:染色体位串长度L，群体规模N，交叉概率pc，变异概率对于本文，位串长度L已经由聚类个数决定，所以，只讨论群体规模N、交叉概率pc和变异概率pm。本文使用控制变量法分别对这3个参数进行实验。

(1)群体规模N

假设样本集合的个数为m，分别设置群体规模N为m，2m，3m对算法聚类结果和收敛性进行评估和分析。本次实验选择的测试数据集为D3。实验结果如表3所示，表中数据皆为多次运行结果的平均值。

表3 群体规模实验结果

对每一代种群中的个体的均值方差定义为:

其中，xi表示每个个体的聚类评价值;¯x为每一代种群中所有个体聚类评价值的平均值;n表示种群数量。

由实验结果可以得到3次实验遗传算法的收敛性折线图，如图1所示。

图1 算法收敛性折线图

分析折线图可以发现，种群数量越大，整个遗传算法的收敛速度越慢，从而可以有效防止成熟前收敛。当群体规模为m时，其收敛代数大致在第8代;规模为2m时，收敛在第11代;而当规模为3m时，在第13代收敛。从遗传算法的特性来看，越晚收敛，越能保持种群的多样性，进而增加了遗传算法搜索全局最优解的概率。同时，本文结合3次实验的准确率、召回率、F度量以及聚类有效性指标进行分析，当群体规模为2m和3m时，不管是准确率、召回率、F度量还是聚类有效性指标都要优于群体规模为m时的情况。而群体规模为2m和3m则相差不大，虽然3m的群体规模的聚类质量稍略优于2m，但是当规模为3m时，它的计算量明显要高出很多。所以综合考虑，本文采取的选择种群规模N=2m，是一个合理有效的选择指标。

(2)交叉概率pc和变异概率pm

交叉概率pc控制着遗传算法中交叉算子的运行频率，而每一代的规模为n的群体中，有pc×n个染色体进行交叉操作，交叉概率越大，种群中的不同个体的染色体基因结构交换越频繁，容易形成新的个体，但是已经获得的优良基因丢失的概率也可能增大。变异算子对群体保持多样性起到了很大的作用。对于长度为k的染色体，每一代的种群中发生变异的次数为pm×k×n。同样的，变异概率的选择也很重要，如果变异概率过大，则会使得整个遗传算法转变为随机搜索;相反，变异概率太小，又无法发挥变异算子的作用，不能有效保持种群的多样性。从一些经验分析来看，交叉概率的取值一般是pc=0．6 ～1．0，变异概率的取值为 pm=0．01 ～0．10［16］。本文根据实际情况，利用实验数据D4，选取了一些交叉概率和变异概率的取值组合来进行实验。为了让数据更加接近实际情况，笔者进行多次实验并计算所有数据的平均值，结果如表4所示。

表4 交叉概率和变异概率实验结果

分别对非常多组合的不同的交叉概率和变异概率的取值进行实验，这里只列出了效果比较好的3个取值组合，最终取交叉概率pc=0．95以及变异概率pm=0．07。事实上，在遗传算法中，交叉概率和变异概率针对不同的应用和解决不同的问题并没有一致的取值，它们应该根据实际问题来进行决定。从实验结果来看，这3组交叉概率和变异概率的选择，聚类结果基本相同，但是在聚类质量指标上有一定的差异。这种聚类质量的差异对聚类结果的影响将随着数据规模的增大而增大。

7．3 与标准k-medoids算法的比较

根据以上的实验确定的遗传算法的控制参数，选取数据规模2m、交叉概率pc=0．95以及变异概率pm=0．07作为本文实验的参数。另外，为了验证本文算法的有效性，把结合了遗传算法的k-medoids和标准的k-medoids算法进行了比较。同时，针对相同的实验数据，笔者把标准的 k-medoids算法运行100次，并取其最好的结果来进行比较分析。实验结果如表5所示。

表5 不同算法的实验结果对比

从2次实验数据D3和D5的验证中可以得出，本文的遗传算法在与k-medoids聚类算法的结合中，确实发挥了其优化算法的作用，也在一定程度起到了搜索全局最优解的能力。

如果就时间性能上来分析，标准的k-medoids算法在效率上要明显优于本文提出的遗传算法。因为在本文算法中，每一次的个体适应度的计算都是要运行一次k-medoids算法。加入遗传算法是以时间换聚类质量，通过底层不断地搜索更优的聚类中心点，并用k-medoids进行聚类，利用遗传算法的全局搜索能力最后得到最优解。

8 结束语

在XML聚类中较常用的是基于划分的聚类算法，但是基于划分的聚类算法面临着2个问题:(1)聚类个数要作为输入参数，算法并不能够自动确定;(2)初始聚类中心点的选择。针对这2个问题，本文分别提出了解决的方案。首先，对于聚类个数的确定问题，利用XML文档数据集的相似度，在不同的阈值下通过基于模糊等价关系矩阵的方法进行聚类，并且每次聚类结果用预先定义的聚类评价函数进行评估，最后把聚类评估值最高的聚类结果对应的聚类个数作为所需确定的聚类个数。实验结果证明了该方法的准确性和快速性。对于初始聚类中心点问题，由于k-medoids算法的初始聚类中心点是随机选择的，无法保证其是最佳的聚类中心点，因此本文采用了遗传算法和k-medoids相结合的算法，利用遗传算法具有搜索全局最优解的能力，对随机的初始聚类中心点进行优化，最后根据算法收敛，输出最佳聚类结果。针对这个过程，本文通过不同的实验数据进行多次验证，表明了算法的有效性。同时对影响遗传算法性能的一些重要参数进行了相关的实验，以确定合适的参数，保证聚类结果的质量。

虽然遗传算法与k-medoids算法的结合在XML文档聚类中能取得不错聚类效果，但是遗传算法本身由于计算量大，时间花费上较其他算法要更多。因此，下一步工作是在保证聚类质量的前提下，减少遗传算法的计算量，提高XML文档聚类效率。

［1］ Abiteboul S，Buneman P，Suciu D．Data on the Web［M］．San Francisco，USA:Morgan Kaufmann，2000．

［2］孟小峰．XML数据管理:概念与技术［M］．北京:清华大学出版社，2009．

［3］ Mazuran M，Quintarelli E，Tanca L．Data Mining for XML Query-answering Support［J］．IEEE Transactions on KnowledgeandDataEngineering，2012，24(8):1393-1407．

［4］ Han Jiawei，Chang K C．Data Mining for Web Intelligence［J］．Computer，2002，35(11):64-70．

［5］ Wang Lian，Mamoulis N，Cheung D W，et al．Indexing Useful Structural Patterns for XML Query Processing［J］．IEEE Transactions on Knowledge and Data Engineering，2005，17(7):997-1009．

［6］ Lloyd S P．Least Squares Quantization in PCM［J］．IEEE Transactions on Information Theory，1982，28(2):129-137．

［7］ Kaufman L，Rousseeuw P J．Finding Groups in Data:An Introduction to Cluster Analysis［EB/OL］．(2008-05-27)．http://as． wiley． com/WileyCDA/WileyTitle/productCd-0471735787．html．

［8］ Nayak R．Investigating Semantic Measures in XML Clustering［C］//Proceedings of2006 IEEE/WIC/ACM InternationalConference on Web Intelligence．Washington D．C．，USA:IEEE Press，2006:1042-1045．

［9］ Shasha D，Wang J T L，Zhang Kaizhong，et al．Exact and Approximate Algorithms for Unordered Tree Matching［J］．IEEE Transactions on Systems，Man and Cybernetics，1994，24(4):668-678．

［10］ Zhang Kaizhong，Statman R，Shasha D．On the Editing Distance Between Unordered Labeled Trees［J］．Information Processing Letters，1992，42(3):133-139．

［11］ Choi I，Moon B，Kim H J．A Clustering Method Based on Path Similarities of XML Data［J］．Data ＆ Knowledge Engineering，2007，60(2):361-376．

［12］ Joshi S，Agrawal N，Krishnapuram R，et al．A Bag of Paths ModelforMeasuring StructuralSimilarity in Web Documents［C］//Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and DataMining．NewYork，USA:ACM Press，2003:577-582．

［13］朴勇，王秀坤．一种 XML文档结构相似度计算方法［J］．控制与决策，2010，25(4):497-501．

［14］ Sheng Weiguo，Liu Xiaohui． A Genetic k-medoids Clustering Algorithm［J］．Journal of Heuristics，2006，12(6):447-466．

［15］ Wu Jianan，Zhou Chunguang，Li Zhangxu，et al．A Novel Algorithm for Generating Simulated Genetic Data Based on k-medoids［C］//Proceedings of the 2nd International Conference on Cloud Computing and Intelligent Systems．Washington D．C．，USA:IEEE Press，2012:25-28．

［16］李敏强，寇纪淞，林丹，等．遗传算法的基本理论与应用［M］．北京:科学出版社，2002．