一个新的指定验证者聚合签名方案
2015-01-02陈建能
陈建能
(闽南师范大学 计算机学院,福建 漳州 363000)
1 引言
在2003年的欧洲密码学国际会议上,Gentry[1]第一个提出了基于证书加密的密码学体制,在该密码学体制下,每一个签名者都会有自己的公钥、私钥、一个证书.该证书必须是由权威机构认证并且颁发的.证书和私钥在生成签名时必需使用,而公钥在对签名进行验证时必需使用.在生成用户私钥时,签名者自己挑选一个随机值作为自己的秘密私钥,所以不会存在基于身份秘密学体制下的密钥托管问题.第二年,Kang,Park和Hahn[2]等人一起提出了基于证书签名的概念并用两个具体的签名方案进行说明.到了2007年,Li,HUANG,MU,SUSILO[3]等最先提出基于证书的替换公钥攻击并定义了相关的安全模型.第二年,Liu,BAEK和SUSILO[4]提出一个没有双线性对的基于证书签名方案和一个在标准模型下证明其安全性的方案.过后不久,Zhang在文献[5]中证明了Liu等人方案是不安全的,并提出了一个改进方案.第三年,Wei Wu和Yi Mu[6]提出了一种新的基于证书数字签名的安全结构,该结构基于证书和无证书都通用.2011年,JiGuo Li[7]等人提出了一个高效的基于证书短签名方案,在该方案中证书需要保密.2013年,陈建能[8]等人提出了一个可证明安全的基于证书签名方案,并在随机预言机模型下证明其安全性.
Boneh,Gentry和Lynn在文献[9]中首先提出聚合签名的思想.第二年,Lysyanskaya,Micali,Reyzin,和 Shacham[10]提出了一个有顺序的聚合签名方法,第一个签名者生成签名之后,第二个签名者必需在第一个签名的基础上才能聚合.过了两年,Lu,Ostrovsky和Sahai[11]提出了没有使用随机预言机模型下的聚合签名方法.到了2009年,Liu[12]首先提出了一个基于证书的有序聚合签名方案.2013年,Lee等人[13]提出了一个有序聚合签名方案具有较短的公钥,并且在标准模型下证明了其安全性.本文根据基于证书聚合签名思想结合指定验证者签名的优点,构造了一个新的基于证书指定验证者聚合签名方案.
2 困难性问题
计算性Diffie-Hellman问题(CDHP:Computational Diffie-Hellman Problem):在的加法循环群G1中,其生成元为大素数P,已知aP,bP,计算出abP的值,我们称之为计算性Diffie-Hellman困难问题.
离散对数问题:对于已知的整数b和素数P,q,求一个整数a,使得等式b=aP mod q成立.
在本文中我们假设要解计算性Diffie-Hellman问题是困难的.解离散对数问题也是困难的.
3 具体的签名方案
3.1 系统参数的建立
选择一个双线性对e,两个加法循环群G1和G2,大素数P是加法循环群G1的一个生成元.认证中心在整数域上选取一个随机值s作为认证系统的私钥,认证系统的公钥通过等式PKc=sP来计算.认证中心再选择三个公开无碰撞的杂凑函数,
H1:{0,1}*→G1,H2:{0,1}*×G1→G1,
H3:{0,1}*×G1→Zq*,认证中心公开所有系统参数(G1,G2,e,q,P,PKc,H1,H2,H3).
3.2 签名密钥的生成
每一个签名者具有唯一的一个身份,我们用IDi来表示该身份信息,下标i大于等于1,小于等于n,n是所有参与聚合签名的总人数.签名者首先要整数域上选取一个随机值xi作为自己的私钥,然后通过等式PKi=xiP计算出自己的公钥PKi.
3.3 证书颁发过程
每一个参与聚合的签名者都要把跟自己身份的相关信息,例如公钥,身份等,提交给认证中心,认证中心首先验证签名者发送来的信息的是否真实,如果信息是真实的,再验证身份有没有重复,如果没有,则把用户公钥,系统公钥和用户身份信息输入杂凑函数,计算出Qi=H1(PKc,PKi,IDi)和certi=sQi,然后把证书certi发送给对应的签名者.
3.4 签名的生成
对于某个具体的消息mi,签名者首先在整数域中随机选择一个ri,并计算以下数值:
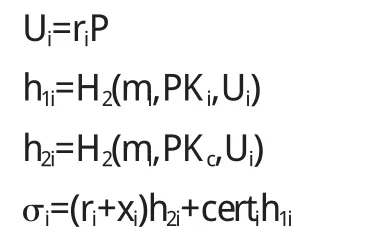
然后把签名结果σi=(U,σi)发送给签名聚合者,签名聚合者收到第i个签名之后,对等式e(P,σi)=e(Ui+PKi,h2i)e(h1iQi,PKc)是否成立进行验证,若等式成立则认为该签名是合法的,否则是不合法的.所有用户把各自的签名发送给聚合者,聚合者都验证通过之后,聚合者才计算σ=H3(e(σ1,Y),e(σ2,Y)…e(σn,Y))其中Y是聚合签名所指定的那个验证者对应的公钥,并生成最后的聚合签名结果(U1,U2,…Un,σ)并发布该聚合签名.
3.5 签名的验证过程
签名的指定验证者收到签名之后验证等式
σ=H3成不成立,如果等式不成立,验证者就认为该签名是一个不合法的聚合签名.如果等式成立就认为该签名是n个用户对消息的聚合签名.
4 正确性和不可伪造性分析
4.1 正确性分析
根据以上的签名验证过程,我们可以得出下面的结果:
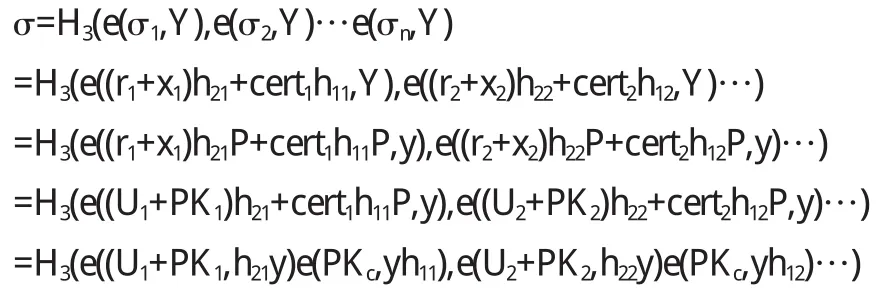
所以我们可以判断验证等式是正确的.
4.2 不可伪造性分析
在基于证书签名中,存在两类敌手,第一类型敌手AⅠ,知道所有签名用户的公钥和对应的私钥,唯一的限制是他不能知道目标身份所对应的签名者的证书,所以在通过正常途径生成该目标用户签名时,敌手AⅠ就得伪造一个证书certi,如果敌手AⅠ能成功伪造一个证书certi,我们就能解离散对数困难问题.而对于第二类型的敌手AⅡ,所有签名者的证书他都知道,唯一的限制是他不能知道目标身份用户的私钥,这样他要伪造聚合签名就等同于伪造单个签名σi.如果敌手想通过破解出某个签名者的私钥来生成签名,则需要破解CDHP问题.所以,该指定验证者聚合签名方案是不可伪造的.
5 结束语
基于证书的数字签名方案没有基于身份签名的秘钥托管问题,也少了传统公钥密码体制下的证书管理问题.本文结合了基于证书的聚合签名思想和指定验证者数字签名优点,提出了一个新的基于证书的指定验证者聚合签名方案.
〔1〕GENTRY C.Certificate-based encryption and the certificate revocation problem[A].EUROCR-YPT 2003[C].Lecture Notes in C-omputer Science,vol.2656,Springer-Verlag,Berlin,2003.272-293.
〔2〕KANG B,PARK J,HAHN S.A certificate-based signature scheme[A].CT-RSA2004[C].Lecture Notes in Computer Science,vol.29-64,Springer-Verlag,Berlin,2004.99-111.
〔3〕LI J,HUANG X,MU Y,SUSILO W.Certificatebased signature:security model and efficient construction[A].EuroPKI2007[C],Lecture Notes in Computer Science,vol.4582,Springer-Verlag,Berlin,2007.110-125.
〔4〕LIU J,BAEK J,SUSILO W.Certificate-based signature schemeswithout pairings or random Oracles[A].ISC2008[C],Lecture Notes in Computer Science,vol.5222,Springer-Verlag,Berlin,2008.285-297.
〔5〕ZHANG J.On the Security of a Certificate-based signature scheme and its improvement with pairings[A].ISPEC2009[C],Lecture Notes in Computer Science,vol.5451,Springer-Verlag,Berlin,2009.47-58.
〔6〕SHAO Z.Certificate-based fair exchange protocolof signatures from pairings[J].Computer Network s 52(2008):3075-3084.
〔7〕LI J G,HUANG X Y,ZHANG Y C.Anefficient short certificate-based signature sc-heme[J].The Journal of Systems and Softw-are.85(2012):314-322.
〔8〕陈建能,岳昊,黄振杰.一个可证安全的基于证书聚合签名方案[J].计算机工程与应用,2013(21):60-64.
〔9〕BONEH D,GENTRY C,Lynn B.Aggregate and verifiably encrypted signaturesfro-m bilinear maps[A].Cryptology-Eurocrypt’03[C].Berlin:SpringerVerlag,2003.416-432.
〔10〕A.Lysyanskaya,S.Micali,L.Reyzin,H.Shacham,Sequential aggregate signaturesfrom trapdoor permutations,in:C.Cachin,J.Camenisch(Eds.),Eurocrypt 2004,LNCS3027,Springer-Verlag,Interlaken,Switzerland,2004:74–90.
〔11〕Lu S,Ostrovsky R,Sahai A,et al.Sequential Aggregate Signatures and Multisignatures Without Random Oracles[C]//Proc.of EURO-CRYPT’06.Berlin,Germany:Springer-Verlag,2006:465-485.
〔12〕Liu J K,Back J,Zhou J.Certificate-based Sequentialaggregate Signature [C]//Proceedings of WiSec’09.New York:ACM,2009:21—28.
〔13〕Kwangsu Lee,Dong Hoon Lee,Moti Yung. Sequential Aggregate Signatures with Short Public Keys:Design,Analysis and Implementation Studies.Public-Key Cryptography–PKC2013.Lecture Notes in Computer ScienceVolume7778,2013,pp 423-442.
