面向智能交通的多路径调度网络模型解析
2014-12-31秦维洋
秦维洋
(中国电信股份有限公司上海研究院 上海 200122)
1 车辆调度网络的现状
在现实世界,车辆调度是解决突发事件、应急事件等问题的重要研究课题,在智能交通领域更是研究的热点。目前,国内外诸多专家学者纷纷对车辆调度问题进行研究。
王旭[1]等人通过分析调度问题的需求信息提出顺序,将动态调度问题等效为不同时刻的静态调度,并建立了基于时间轴的动态调度模型,设计了“初始优化阶段+实时优化阶段”的分段求解策略;唐伟勤[2]等人通过对应急车辆调度路径的研究,以调度所花费时间的均衡性为目标建立了调度模型,并结合实例改进了最近搜索法;王晓博[3]等人建立了多车型、多车场的混合车辆导读模型,运用混合遗传启发式算法对车辆调度问题进行求解;张景玲[4]等人考虑了物流配送中需求的动态变化、车型、路线等,建立了数学规划调度模型,制定了预优化路径调度和实时调度策略,提出了2-OPT优化方法,提高了算法的收敛速度;刘芹[5]等人基于实际交通状况提出了改进的车辆调度模型,并运用粒子群算法和模拟退火算法混合求解了调度问题;何正文[6]等人基于禁止时间窗的应急物资调度问题,通过整数规划优化了调度模型,并定义了相关决策变量,对路径的节点和支线进行选择;王文蕊[7]等人从实际配送中变化的订货量出发,提出了变动成本概念,引入预优化策略,建立了能够根据订货量变化实时调整的两阶段数学模型,并采用粒子群算法求解调度模型,验证了两阶段模型的有效性;何建敏[8]等人基于调度问题中的时间紧迫性与车辆出发地数目相互矛盾的目标,运用模糊优化方法研究了限制期下的多出救点组合模型;赵燕伟[9]等人通过建立基于模糊满意度的多目标数学规划模型来优化车辆调度问题,提出利用分段优化的方法求解Pareto解,并为保持Pareto解的分散性,提出了一种自适应网格算子;安一帆[10]结合道路交通情况,建立了包含时间影响因素的结构模型,从而实现调度时间的优化。
Sangheon HAN[11]等人考虑到利用遗传算法计算车辆调度问题的收敛速度,提出了一种结合遗传算法与其他启发式算法的混合算法来解决车辆调度问题;William Ho[12]等人为解决多车场多路径的调度问题,提出了一种混合遗传算法,并验证了算法的有效性;Ombuki B[13]等人用遗传算法求解多目标调度问题,考虑了车辆数量和距离成本,从两个维度验证了算法的可靠性;Jin M Z[14]等人提出了一种时延最小的数学规划模型,并通过线性规划提高了模型的性能指标。
上述研究内容包含大量车辆调度问题的研究成果及应用,为多路径车辆调度问题的动态描述和求解提供了很好的思路,对建立和完善多路径车辆调度模型有很好的借鉴意义。
2 多路径调度网络建模
2.1 多路径调度网络的定义
在智能交通领域,多路径的车辆调度网络是一个由车辆出发地(S)、目的地(D)和连接路径(P)组成的网络。在复杂的多路径调度网中,调度目的地是构建车辆调度网络的诱因,也是车辆调度系统建模的首要元素,在调度过程中提出调度需求的类型、数量、时间等;车辆出发地是构建车辆调度网络的必备条件,是建模的重要元素,必须具备一定数量相同类型或不同类型的车辆,能够为车辆调度提供一定类型、数量的有效车辆;连接路径是网络中车辆进行有效调度的激活条件,是车辆出发地和目的地之间建立联系的必要元素,只有两者存在有效连接,车辆的调度需求才能得到满足。
在实际的调度网络中,车辆调度是一个实时的动态过程,调度目标有可能会发生改变,导致车辆数量增减、调度目的地变更等。如在调度中,由于天气、人为等因素的影响,调度策略需要做出修改和调整,可能出现已经出发的车辆虽然未到达目的地,但需要执行新的调度方案,原来未建立有效连接路径的两点间可以直接连接或通过间接路径连接。此时,原有模型中的节点、连接路径不能很好地体现此时调度网络的实际特征和性质。因此,模型中还应包含表征多路径、多类型车辆、多目的地以及动态因素的建模元素。
本文引入虚拟节点和虚拟路径的概念对调度过程中的动态特征进行描述,并给出多路径车辆调度网的形式化定义。多路径车辆调度网是一个满足如下条件的六元组N=(S,Sv,D,P,Pv,M):
·S={s1,s2,…}是一个有限的车辆出发地集合,其中S≠;
·Sv={sv1,sv2,…}是一个有限的车辆出发地集合,其中Sv可以为空;
·Dv={dv1,dv2,…}是一个有限的目的地集合,其中Dv可以为空;
·P={p1,p2,…}是一个有限的连接路径集合,其中P≠且P是((S∪Sv)∪D)×((S∪Sv)∪D)的多重子集;
·Pv={pv1,pv2,…}是一个有限的连接路径集合,其中Pv可以为空;
·M:P∪Pv→{(a,b)|a∈(S∪Sv)∪D,b∈(S∪Sv)∪D,a≠b}是连接路径P∪Pv到无序积((S∪Sv)∪D)&((S∪Sv)∪D)的映射,表示车辆出发地与目的地之间的连接关系;
· 存在M(pi)=(a,b),M(pj)=(a,b),其中a∈((S∪Sv)∪D),b∈((S∪Sv)∪D),且a≠b,表示网络中两点间存在多条路径;
·dom(P)∪cod(P)=(S∪Sv)∪D,其中dom(P)={a|埚b:(a,b)∈P},cod(P)={b|埚a:(a,b)∈P}。
上述定义中S和D分别代表车辆出发地、目的地,是网络的基本元素。其中S≠ 、D≠ 表示在调度网络中至少存在一个车辆出发地和一个目的地,同时P≠ 是((S∪Sv)∪D)×((S∪Sv)∪D)的子集,表示网络中不存在独立的出发地或目 的地,M(p)=(a,b),a∈(S∪D),b∈(S∪D),a≠b,p∈P,表示网络中没有无意义的自环。M是网络中任意两点间的映射,对于M(pi)=(a,b),M(pj)=(a,b),若M(pi)≠M(pj),表示网络中两点间存在的多条路径中,包含的映射函数是不同的;若M(pi)=M(pj),表示网络中两点间存在的多条路径,包含的映射函数是相同的。若Sv≠ ,Dv≠ ,则调度网络表示最基本的车辆调度网络。
2.2 多路径调度网络结构
节点和路径是多路径调度网络中重要的组成元素,而网络中很多结构特性也是通过节点、路径的种类和连接关系来反映的。下面从节点和路径两个角度分析多路径调度网络结构特征。
(1)路径角度
路径表示节点间复杂的关联关系,在不同的网络中,路径也会根据连接关系、限制条件等因素划分为不同的类型,如多路径调度网络中的路径可以分为公路、铁路、水路、航空线路等类型。
如图1所示,多路径调度网络的连接路径包含两种情况。
· 如图1(a)所示,网络中只有一种类型的路径,即网络中任意两个节点的连接路径只有单一类型,包含出发地之间和目的地之间,是车辆调度网络中一种基本的结构类型。
· 如果1(b)所示,网络中存在多种类型的连接路径。对于网络中任意两个关联节点可能包含两种情况:两节点间有多重连接路径,但每两个节点间的路径只有一种类型;两节点间有多重连接路径,两节点间连接路径的类型也不相同。

图1 多路径调度网络的连接路径
(2)节点角度
多路径调度网络中节点的度表示与该节点连接的连接路径数量,也是网络结构特征的基本参数。如图2所示,当节点入度为0、出度不为0时,表示该节点在网络中仅作为车辆出发地,如节点s3;当节点入度不为0、出度为0时,表示该节点在网络中仅作为目的地,如节点d4;当节点入度和出度均不为0时,表示该节点有可能同时作为车辆出发地和目的地,如节点d5。

图2 调度网络中节点的度
在实际的多路径调度网络中,连接路径通常无指定方向,以节点的度作为参考对象,可将连接路径看成一条双向的连接路径,如路径p6。
3 分层调度网络建模
在多路径车辆调度问题中,由于调度优先级等原因,网络结构会呈现出一定的层次性,不同层次的网络结构体现了节点、连接路径及网络结构的层次性。分层调度网络是一个满足如下条件的六元组N=(SD,PD,SH,PH,FPD,FPH):
·SD是一个有限的多层次节点的集合,SD={S1,S2,…},其中,Si={si1,si2,…},i=1,2,…,表示第i层内的节点(|SD|≥2,Si≠ ,i=1,2,…);
·PD是一个有限的连接同层节点的连接路径集合,PD={P1,P2,…},其中,Pi={pi1,pi2,…},i=1,2,…,表示第i层内连接节点的连接路径(|PD|≥2,Pi≠ ,i=1,2,… );
·SH是一个有限的分层网络间节点的集合;
·PH是一个有限的分层网络间的连接路径集合;
·:PD→{(x,y)|x,y∈Si,x≠y,Si哿SD},表示同层连接路径PD到无序积SD&SD(不包含自环)的映射;
·:PH→{(x,y)|x∈Si,y∈Sj,x≠y,i≠j,Si哿SD,Sj哿SD},表示跨层连接路径PH到无序积SD&SD(不包含自环)的映射。
在分层网中,节点分为多个层次,连接路径也相应地分为同层连接和层间连接,同层节点之间按照同层连接规则由同层连接路径进行连接,跨层节点之间的连接关系则由层间连接规则确定。
分层调度网络也具有一定的结构特征,本文定义变量如下:
·HS(S)={hs1,hs2,…},表示分层网络中节点所属的层次集,HS≥1;
·fhs:S→HS(S),表示节点到节点所属层次的划分函数;
· ω(si)=fhs(si),表示节点所属的层次,ω(si)∈HS;
·HP(P)={hp1,hp2,…},表示分层网络中连接路径所属的层次集,HP≥1;
·fhp:P→HP(P),表示连接路径到连接路径所属层次的划分函数;
· ω(pi)=fhp(pi),表示连接路径所属的层次,ω(pi)∈HP。
在分层调度网络中,任意两个节点间存在层次差,用DHS(si,sj)=ω(si)-ω(sj)表示。若DHS(si,sj)>0,即 ω(si)>ω(sj),则表示节点si所属的层次大于节点sj所属的层次;若DHS(si,sj)<0,即ω(si)<ω(sj),则表示节点si所属的层次小于节点sj所属的层次;若DHS(si,sj)=0,即 ω(si)=ω(sj),则表示节点si与节点sj属同一层次;若DHS(si,sj)=1,表示两节点是邻层节点;若DHS(si,sj)>1,表示两节点是跨层节点。
同理,分层调度网络中的连接路径也存在上述情况,用DES(pi,pj)=ω(pi)-ω(pj)表示连接路径的层次差。若DES(pi,pj)>0,即ω(pi)>ω(pj),则表示连接路径pi所属的层次大于连接路径pj所属的层次;若DES(pi,pj)<0,即 ω(pi)<ω(pj),则表示连接路径pi所属的层次小于连接路径pj所属的层次;若DES(pi,pj)=0,即 ω(pi)=ω(pj),则表示连接路径pi与连接路径pj所属的层次相同;若DES(pi,pj)=1,表示两条连接路径是邻层连接路径;若DES(pi,pj)>1,表示两条连接路径是跨层连接路径。
定义Vad(si)={uj|uj∈S-si,(si,sj)∈F(P)},表示节点si的邻接节点集合;VadS(si)={uj|uj∈Vad(si),ω(uj)=ω(si)},表示节点si的处于同层的邻接节点集;VadD(si)={uj|uj∈Vad(si),ω(uj)≠ω(si)},表示节点si的处于不同层的邻接节点集。其中,Vad(si)=VadS(si)∪VadD(si)。
(1)从邻接节点数量分析
·当存在|VadS(si)|=1时,表示节点si只与同层次中的一个节点连接。
·当存在|VadS(si)|>1时,表示节点si与同层次中的多个节点连接。
·当存在|VadD(si)|=1时,表示节点si只与其他层次中的一个节点连接。
·当存在|VadD(si)|>1时,表示节点si与其他层次中的多个节点连接。
(2)从邻接节点层次差分析
在同层邻接节点集VadS(si)中,DHS(si,uj)=0。
在不同层邻接节点集VadD(si)中,若DHS(si,uj)=1,表示在不同层邻接节点集中存在与节点si连接的邻层节点;若DHS(si,uj)>1,表示在不同层邻接节点集中存在与节点si连接的跨层节点。
图3为一个分层调度网络结构,该分层调度网N=(SD,PD,SH,PH,,)描述如下 :SD={S1,S2,S3},其中,S1={s1,d1,s2,d2,s3,d3},S2={s4,d4,s5,d5},S3={s6,s7,d6,d7},PD={P1,P2,P3},其 中 ,P1={p1,p2,p3,p4,p5,p6},P2={p8,p11,p12},P3={p24,p25},SH= ,PH={p7,p9,p10,p13,p14,p15,p16,p17,p18,p19,p20,p21,p22,p23}。
从图3中可以看出,第一层网络中存在两种类型的节点,单一类型的连接路径;第二层网络中存在两种类型的节点,3种类型的连接路径;第三层分层网中存在两种类型的节点,单一类型的连接路径。
(1)从节点的角度分析
对于节点s1,其邻接节点集为Vad(s1)={d1,d4,s6,d6},同层的邻接节点集VadS(s1)={d1},不同层的邻接节点集VadS(s1)={d4,s6,d6}。其中,DHS(s1,d1)=0,表示节点s1与节点d1为同层节点且两节点为不同类型;|VadS(s1)|=1,表示节点s1只与同层次中的一个节点连接。|VadD(s1)|=3,表示节点s1与其他层次中的多个节点连接。DHS(d4,s1)=0表示节点s1与节点d4为邻层连接节点,且两节点为不同类型;DHS(s6,s1)=DHV(d6,s1)=2表示节点s1与节点s6、d6为跨层邻接节点。
(2)从连接路径的角度分析
图3中分层调度网络存在不同类型的层间连接路径。对于层间连接路径p20,其两个节点为不同类型的邻层连接节点;对于层间连接路径p18,其连接的两个节点为不同类型的跨层连接节点。
4 多路径调度网络实例求解
图4为某一多路径车辆调度网络。已知网络中有3个车辆出发地,4个车辆目的地,按照实际调度情况及调度优先级对该调度网进行分层,包括第一层和第二层。出发地和目的地之间存在高速公路、一般公路、铁路、水路4种连接路径,对应的运输工具包括大货车、小货车、火车、轮船4类。为了提高调度的响应效率,以调度时间最短为目标。由于在车辆调度过程中调度策略发生变化,引入了虚拟车辆出发地和虚拟连接路径来完善该分层调度网络。

图3 分层调度网络结构

图4 多路径车辆调度网络示例
根据以上情况,对图4所示分层调度网进行描述:SD={S1,S2},其 中 ,S1={s1,sv1,d1,d2,d3},S2={s2,s3,d4},PD={P1,P2}其 中 ,P1={p1,p2,p3,p4,p6,p7},P2={p13,p14,p15},SH= ,PH={p5,p8,p9,p10,p11,p12,p16,pv1}。
图4中,车辆出发地与目的地之间连接路径P的邻接矩阵为:
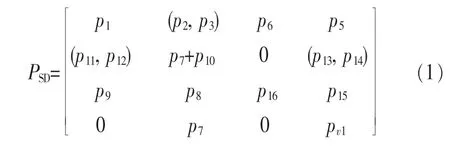
其中,矩阵中的任一元素pij表示车辆出发地si与目的地dj之间的连接路径集合。
每一条连接路径的路径编号、连接节点、路径类型及路径长度等信息见表1。
上述分层调度实例具有多个结构对象,其在调度过程中的组织结构、元素对象等也会发生变化,在求解这类问题时希望能够得到符合目标的最优结果。分层调度问题也可以看作求解最优调度策略问题。因此,采用遗传算法对分层调度问题实例进行求解,通过对初始化种群的评价,择优选择较好的种群进行交叉编译,产生新的种群,然后按照该顺序重复计算,直至达到总体收敛条件,求解出最优方案。

表1 路径信息
算法编码采用(
其中,车辆出发地储备的各类车辆数量与输出的车辆数量情况见表2。

表2 车辆出发地车辆储备数量与输出数量对照
目的地对各类车辆的需求数量与实际接收到的各类车辆数量情况见表3。
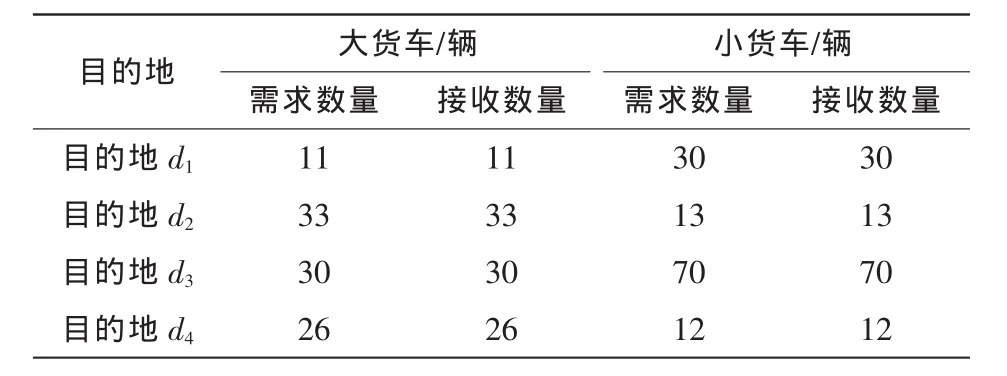
表3 目的地对各类车辆需求数量与接收到的数量对照
从表2和表3可以看出,各出发地能够有效地输出自身储备的车辆,且输出量不大于自身储备量。而目的地也能及时接收到其需求的各类车辆,需求被满足。
通过上述实例,本文的多路径车辆调度模型具有有效性,并能够在原有基础上通过引入虚拟节点、虚拟连接边等建模元素进行扩展,同时能够很好地应用于多层次调度等实际问题。
1 王旭,葛显龙,代应.基于两阶段求解算法的动态车辆调度问题研究.控制与决策,2012,27(2):175~181
2 唐伟勤,张隐,张敏.大规模突发事件应急物资调度中的车辆路径问题.物流技术,2008,27(12)
3 王晓博,李一军.多车场多车型装卸混合车辆路径问题研究.控制与决策,2009,24(12)
4 张景玲,赵燕伟,王海燕.多车型动态需求车辆路径问题建模及优化.计算机集成制造系统,2010,16(3)
5 刘芹,史忠科.混合粒子群算法求解交通路网中的车辆调度问题.控制与决策,2006,21(11)
6 何正文,贾涛,徐渝.基于禁止时间窗的应急物资调度车辆路径问题.运筹与管理,2009,18(12)
7 王文蕊,吴耀华.考虑变动成本的车辆路径问题建模及求解.计算机集成制造系统,2014,20(4)
8 何建敏,刘春林.限制期条件下应急车辆调度问题的模糊优化方法.控制与决策,2001,16(3)
9 赵燕伟,李川.一种新的求解多目标随机需求车辆路径问题的算法.计算机集成制造系统,2012,18(3)
10 安一帆.应急车辆调度中的最优路径研究.技术应用,2013(2)
11 Sangheon HAN,Tabata Y.A hybrid genetic algorithm for the vehicle routing problem with controlling lethal gene.Asia Pacific Management Review,2002(7)
12 William Ho,George T S Ho.A hybrid genetic algorithm for the multi-depot vehicle routing problem.Engineering Applications of Artificial Intelligence,2008(2)
13 Ombuki B,Ross B J.Multi-objective genetic algorithms for vehicle routing problem with time windows.Applied Intelligence,2006(1)
14 Jin M Z.Optimal routing of vehicles with communication capabilities in disasters.Comput Manag Sci,2010(7):121~137
