基于ARMA模型的运城市果蔬肉类价格预测研究
2014-12-28赵婧婧王宝丽姚喜妍
赵婧婧,王宝丽,姚喜妍
(运城学院应用数学系,山西运城044000)
果品、蔬菜与肉类是我国居民日常生活的重要消费品,也是支撑农村经济发展的一个重要产业,各级各类相关管理部门非常重视果蔬肉的生产、供应与销售。各级政府管理部门更是关注果蔬肉的价格波动,并将保持果蔬肉价格稳定作为一项重要职责。如何对果蔬肉市场未来的运行状况进行预测,以确保果蔬肉市场的平稳运行和保障果农、菜农、养殖农户的收入和消费者生活的稳定,逐渐成为社会各界关注的热点和研究界研究的焦点之一。
产品的价格预测是基于时间序列数据的。基于时间序列数据的预测方法有很多种,最常用的技术有分解分析法、回归分析法、移动平均法、指数平滑法、自适应过滤法、小波分频技术、混沌时间序列法、自回归滑动平均模型等[1]。ARMA(Auto-Regressive and Moving Average Model)是一类常见的随机时间序列模型,它是自回归模型(AR模型)和移动平均模型(MA模型)的结合,是对时间序列数据进行预测的较为科学的计量经济学方法之一。ARMA模型由于其较高的灵活性,预测精度较高而且有很多统计软件工具的支持,因此在很多实际时间序列数据分析任务中应用广泛[2-3]。李瑞莹等基于ARMA模型对某航空公司波音飞机的故障率进行预测,并用实例说明ARMA模型适用于故障率预测[4]。徐亚鹏等运用ARMA模型对ST天一的股票价格进行分析和预测[5]。章晨等利用我国房地产价格的历史数据,构建ARMA模型对2012年房地产价格变化进行较为准确的预测[6]。
为此,笔者随机选取运城市某大型超市的部分果蔬肉类价格周数据作为研究样本(数据来源于运城市农业信息网),样本区间设定为2010年第1周至2012年11月第2周,对序列建立一个合理的预测模型来预测2012年11月第3、4周及2012年12月的部分果蔬价格,并与实际周价格进行比较,获得了较为满意的效果。结果表明,ARMA模型可以对地区果蔬肉价格进行预测,预测结果在一定程度上能够对运城市农业管理部门调控果蔬肉市场的供求关系、农户调整生产结构以及果蔬肉交易商掌握较为准确的交易信息提供可靠的参考依据。
1 自回归滑动平均模型(ARMA模型)
自回归滑动平均模型由美国统计学家Jenkins和Box于20世纪70年代提出,主要用来进行时间序列分析。自回归滑动平均模型是自回归模型与滑动平均模型的结合。
1.1 自回归模型(AR:Auto-regressive)如果表示时间序列的Yt满足以下关系式:
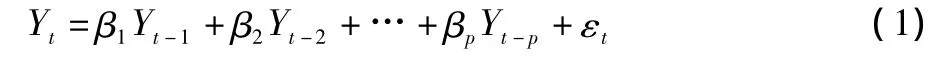
式中,εt表示独立同分布的随机变量序列,而且满足,则称做时间序列y为服从p阶的自回归t模型。
自回归模型的平稳条件:滞后算子多项式φ(B)=1-β1B-β2B2-…-βpBp的所有根都在单位圆外,即φ(B)=0的根大于1。
1.2 滑动平均模型(MA:Moving-Average)如果时间序列yt满足:
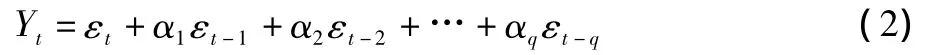
则称时间序列yt为服从q阶移动平均模型。移动平均模型在任何条件下都平稳。
1.3 自回归滑动平均模型(ARMR模型)假定影响因素为 x1,x2…xk,则 Yt=β1x1+β2x2+ … + βpxp+Z,其中,Z 为误差,Yt是预测对象的观测值,受自身变化的影响,其规律可由下式表示:
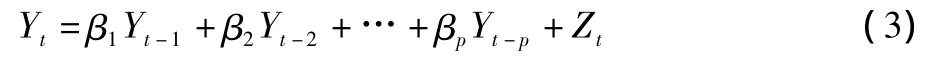
误差项在不同时期具有的关系:

由此,获得ARMA模型关系式:
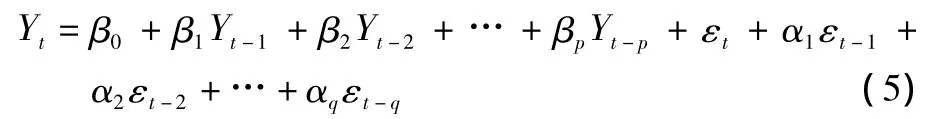
如果时间序列Yt满足:
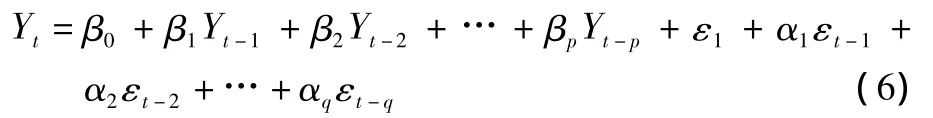
则称时间序列Yt为服从(p,q)阶自回归滑动平均混合模型,亦记为 φ(B)yt=θ(B)εt。
2 ARMA模型价格预测步骤
基于ARMA模型的价格预测可按照以下步骤进行。
2.1 获取数据,并对数据进行预处理首先,获得果蔬肉的价格时间序列,可表示为{p1,p2,…,pt}。然后,绘制价格时间序列变化的曲线图,观察价格变化时候有周期性的变化趋势,若存在,则对数据进行差分处理,形成新序列{Yt}={pt+i-pt},其中,i为周期长度。接着,对现有的时间序列进行零均值化处理,得到零均值化后序列,并对时间序列数据平稳性(此时间序列的一、二阶矩存在且对任意时刻t满足均值为常数、协方差为时间间隔的函数)进行检测。检测时间序列的平稳性的传统方法往往根据其自相关系数的图像进行判别,而此类方法由于存在人为主观性的差异造成判断的准确性局限,该研究利用平稳化的时间序列不存在单位根对其平稳性进行判别。
2.2 建立模型,参数估计在选定选择ARMA(p,q)模型的条件下,需要确定模型的阶数p和q,文献[1]中提供了大量的方法。为了消除人为因素的影响,采用了最小后验信息准则(BIC准则)。确定模型后,可对模型进行定阶,利用许多相关软件如SARS、SPSS、Eviews等软件进行数据计算。确定阶数的同时,软件工具可以辅助计算出各种参数估计,得到预测关系式(6)。
2.3 价格预测最后,运用预测关系式进行下一阶段的价格预测。通常数据越丰富,预测精度越高。
3 实例分析
3.1 原始数据获取到运城市某大型超市2010~2012年11月前2周的部分果蔬肉的周报价格数据。
3.2 数据预处理
3.2.1 检验数据是否存在周期性。图1A~H分别对应大白菜、番茄、大葱、苹果、香蕉、猪肉、鸡蛋、草鱼。从图1可以看出,8种商品的价格变化并没有呈现出周期性。
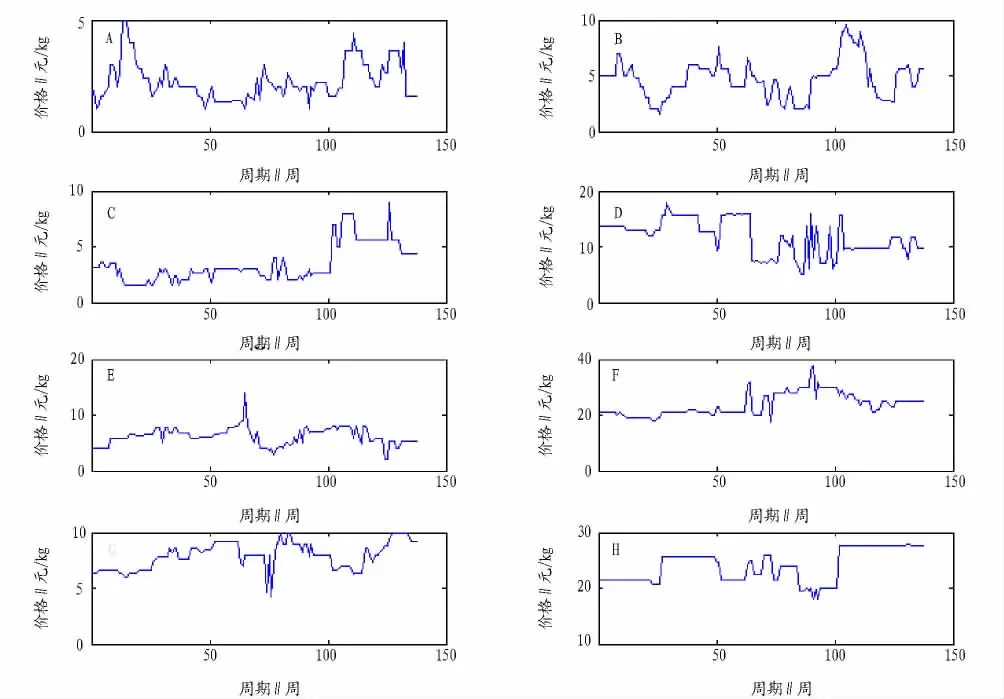
图1 8种商品的价格随时间变化的示意
3.2.2 平稳性检测。根据上一节提出的准则以及统计中的建设检验,对8个时间序列的平稳性进行检验,即:
原假设:时间序列具有单位根(非平稳);
备则假设:时间序列无单位根(平稳)。
利用SAS软件中的宏命令%DFITEST进行计算,结果如表1所示。从表1可以看出,在选定显著性水平0.05的条件下,除了大白菜(本身是平稳的)外其余商品的价格序列在进行一阶差分后均是平稳性时间序列(P<0.05)。
3.3 建立模型
3.3.1 模型阶数的确定。指定 p∈{1,2,3,4,5}和 q∈{1,2,3,4,5}的变化范围下,利用BIC准则得到最优的RAMA模型的阶数。表2为SAS软件计算结果。
3.3.2 模型参数的估计以及参数的显著性检验。利用最小二乘法对模型的参数进行估计,结果如表3所示。
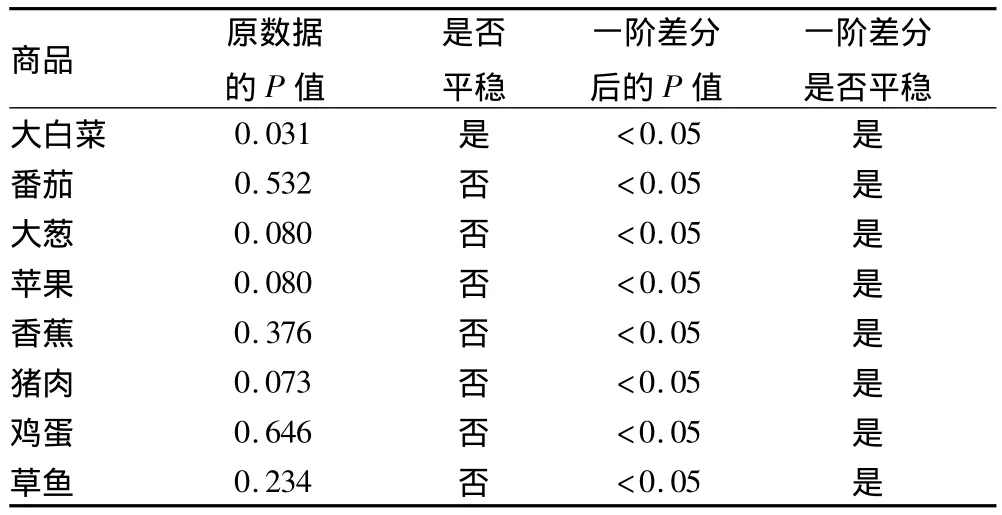
表1 8种商品价格序列的平稳性检验
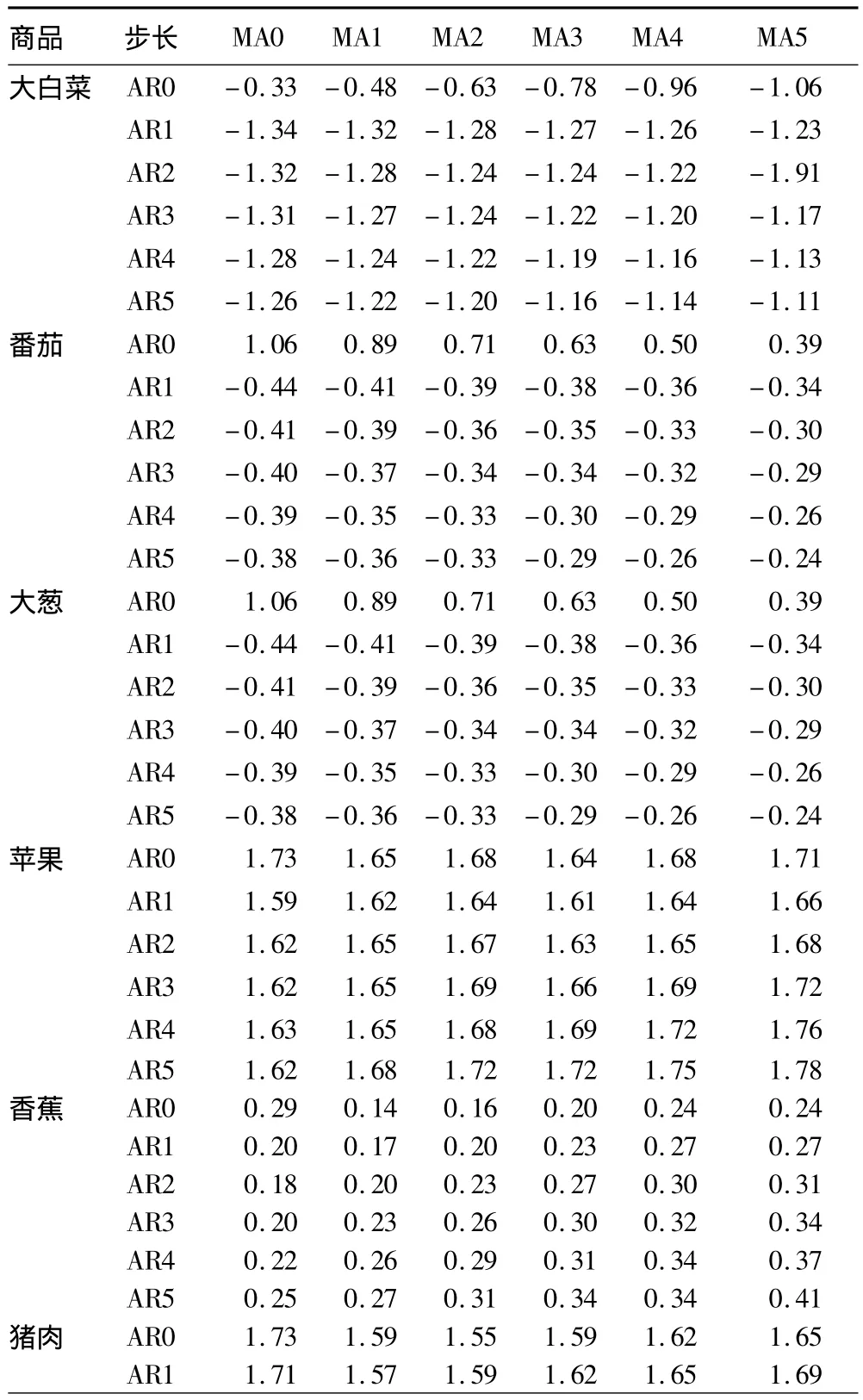
表2 BIC准则得到最优的ARMA模型的阶数
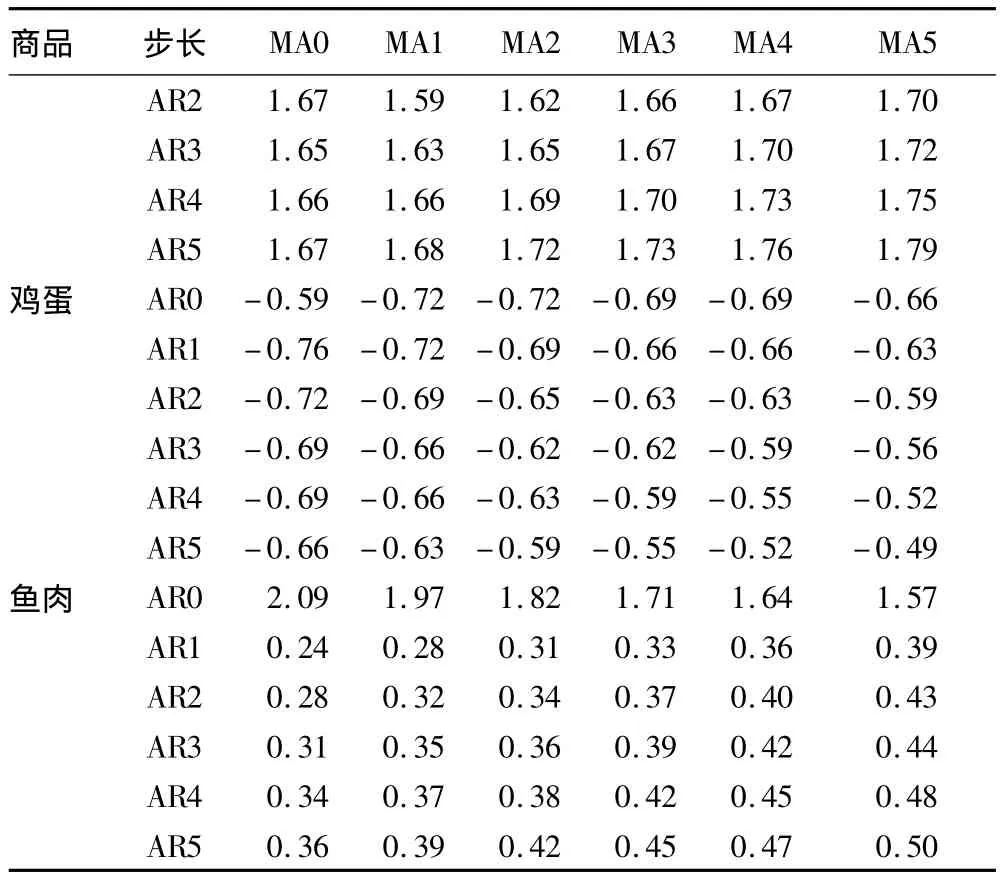
续表2
3.4 预测与比较 将表3中的参数估计值代入式(6),得到预测值如表4所示。95%置信水平下的预测结果见图2。

表3 模型参数的估计
4 总结
ARMA模型是一种比较完善的时间序列建模和分析方法,常用于对时间序列的短期预测。该研究运用ARMA模型对运城市部分果蔬肉类价格进行了预测及对比分析,结果表明其可信并可应用于相应农商管理决策。果品蔬菜肉类的实际价格波动规律还受到国家宏观政策的调控和发展环境的改变等影响,这时,预测误差会有所波动,因此要随时注意这些因素变化,适时根据实际情况得到相对准确的预测值。
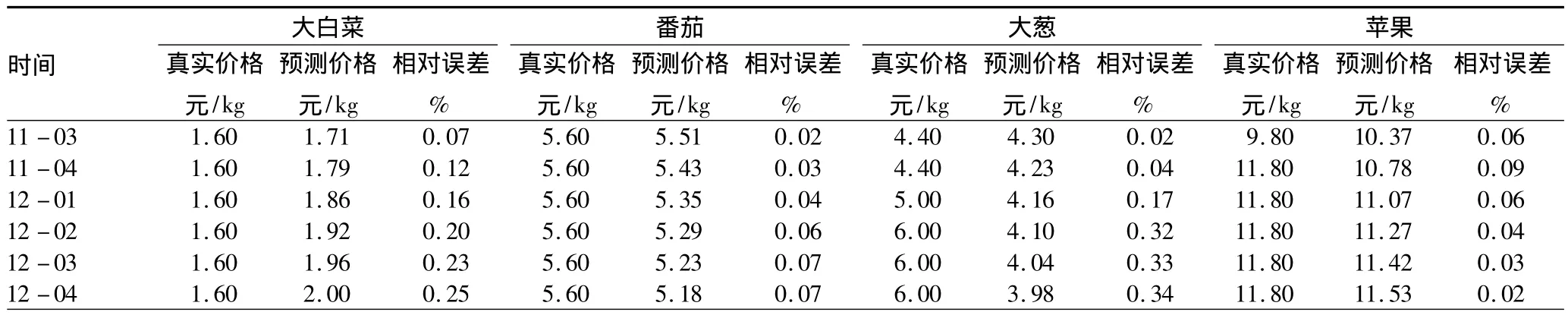
表4 2012年8种商品后6周价格预测

续表4
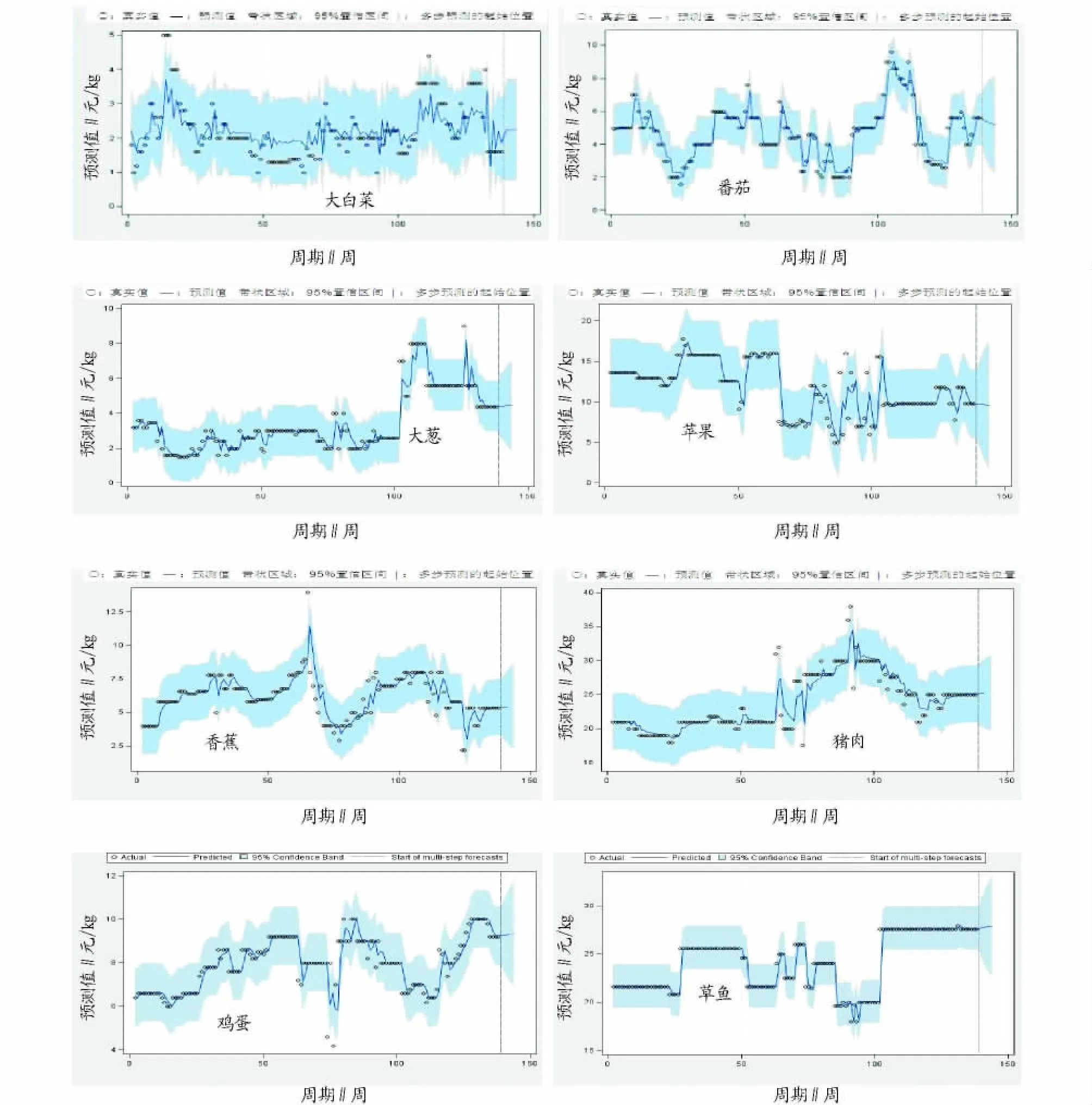
图2 置信水平为95%的价格预测结果
[1]何书元.应用时间序列分析[M].北京:北京大学出版社,2003.
[2]韩雯.ARIMA模型在贵州省农产品价格预测中的应用——以辣椒为例[J].安徽农业科学,2011,39(21):13226 -13227.
[3]邹伯贤,刘强.基于ARMA模型的网络流量预测[J].计算机研究与发展,2002,39(2):1645 -1655.
[4]李瑞莹,康锐.基于ARMA模型的故障率预测方法研究[J].系统工程与电子技术,2008,30(8):1588 -1591.
[5]徐亚鹏,陈贵磊.ARMA模型在股票价格预测中的应用[J].才智,2013(15):2 -3.
[6]章晨,郑循刚,龚沁.基于ARMA模型的我国房地产价格预测分析[J].生产力研究,2012(2):183-185.
[7]葛根,王洪礼,许佳.小波分频技术和混沌时间序列在国际石油价格预测中的应用[J].系统工程理论与实践,2009,29(7):64 -68.
[8]王燕.应用时间序列分析[M].北京:中国人民大学出版社,2012.
