航天器着陆碰撞动力学CUDA并行计算技术

高树义 谷良贤 张方 陈国平 李杨

（1 西北工业大学航天飞行动力学技术重点实验室，西安 710072）（2 南京航空航天大学机械结构力学及控制国家重点实验室，南京 210016）

1 引言

航天器着陆缓冲过程的瞬态分析问题，主要研究结构在碰撞过程的时间历程响应，计算结构在振动时的动位移和动应力的大小，以及变化规律，是结构动力学的一个重要研究方向。物体间的接触碰撞是复杂的力学问题，是引起物体失效和破坏的重要原因。接触碰撞过程在力学上通常涉及三种非线性问题：材料非线性、几何非线性和接触非线性。接触非线性来源于两个方面：接触界面随时间发生变化，要在求解过程中确定；接触条件的非线性。接触条件又包括两个方面：接触体之间在接触面的变形保持协调，即不可贯入性；切向接触的摩擦条件。根据是否考虑接触体的变形，可以将物体间的接触分为刚性接触和弹性接触。在弹性体的接触碰撞分析中，首先要将接触体进行有限元离散；然后将约束条件引入离散系统的运动微分方程，再通过直接积分法或者振型叠加法对系统的响应进行求解。

由于接触碰撞问题涉及非线性问题，并且需要求解时间历程的瞬态响应，其计算过程复杂，计算量大，因此并行计算在这类问题的处理上具有较大的应用价值。文献［1］开发了适应向量机的小球算法；文献［2］设计了三维壳体结构的冲击接触并行算法；文献［3］设计了接触碰撞问题的并行算法；文献［4］在多种并行机型上设计了接触搜索的并行算法，该算法在大规模工程问题上得到了应用。统一计算架构（CUDA）是显卡厂商NVIDIA 在2006年推出的基于图形处理器（GPU）的并行运算平台。其特点是能充分发挥图形显卡的潜力，通过显卡对密集数据实施高效率的并行计算。CUDA 采用C 语言编程，这在很大程度上简化了并行计算的编程，已经被推广应用到某些领域，如分子动力学模拟、计算天体物理的N-Body算法模拟、数字天气预报的加速处理、电磁模拟和地球物理数据处理等。

目前，CUDA 并行算法在航天器着陆碰撞仿真领域还处于研究起步阶段。将并行计算应用到有限元计算上，要从现有的串行算法入手，分析各个环节的并行性，包括有限元模型的建立、计算分析的过程和计算结果的后处理，然后在并行计算平台上设计优良的并行计算程序［5-9］。本文对接触碰撞问题的显式积分计算方法进行了讨论，研究了航天器碰撞问题的并行算法，并通过算例验证了该并行算法的高效性和准确度。

2 接触碰撞问题的显式积分过程

2.1 接触碰撞问题的基本描述

如图1所示，物体A 和B是两个发生接触碰撞的物体，虚线0VA和0VB是它们在接触碰撞之前的位形，tVA和tVB是它们在t时刻发生接触碰撞时的位形，tΓc是这两个物体发生接触碰撞时的接触面，该接触面在两个物体中分别是tΓAc和tΓBc。通常，称物体A 为接触体（Contactor），物体B为目标体或靶体（Target），则tΓAc和tΓBc表示从接触面和主接触面。

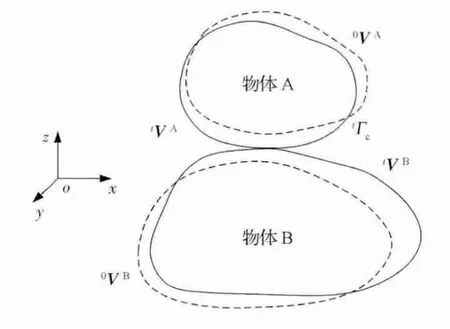
图1 物体A 和B在接触碰撞时的位形Fig.1 Arrangement figure of object A and object B in contact

接触物体在接触面上要满足不可贯穿性和法向接触力为压力的法向接触条件，一般将这两个法向接触条件称作接触碰撞的运动学条件和动力学条件。

2.2 接触问题计算方法

中心差分法是直接积分法的显式求解方法，系统在每一时刻的运动状态可以完全由上一时刻确定，因此可以避免每一增量步的迭代，这在非线性的瞬态分析中具有很重要的意义。由于中心差分法是条件稳定的算法，因此在利用其求解具体问题时，所选取的时间步长Δt必须不大于某个临界步长Δtcr，否则，算法是不稳定的。

中心差分法的稳定性条件为

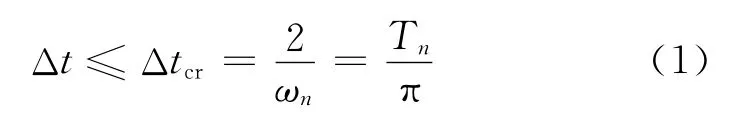
式中：ωn为离散系统的最高阶固有圆频率；Tn为离散系统的最小固有周期；n为阶次。

在利用中心差分法求解接触问题时，其迭代公式为

式中：tu和t＋Δtu分别为t和t＋Δt时刻的位移向量；和分别为t时刻的速度向量和加速度向量；和分别为t＋Δt时刻的速度向量和加速度向量。

从式（2）可以看出，下一增量步的增量解可以完全由上一步确定。

2.3 基于罚函数法的有限元方程计算机实施步骤

在全Lagrange格式下，接触碰撞问题的有限元方程为

式中：M为质量矩阵；t＋ΔtQL和t＋ΔtQc分别为系统在t＋Δt时刻的等效节点力向量和接触力向量；为系统在t＋Δt时刻的节点内力向量。

计算机实施流程简图见图2，具体步骤如下。

（1）令t＝0，并选择积分步长Δt、等效节点力QL、接触力Qc和节点内力F的初值；

（2）形成集中质量矩阵M，并计算M-1；

（5）计算t＋ΔtQL；

（6）由节点内力公式fe＝kTδe计算节点内力的初始值，然后再计算节点应力和节点内力，其中kT为刚度矩阵，δe为节点位移；

（7）搜寻接触点并判断接触点的接触状态；

（8）计算接触力t＋ΔtQc；

（11）令t＝t＋Δt；

（12）若t＜T，返回第4步，否则计算结束。

图2 实施流程Fig.2 Implementation flow chart

3 接触碰撞问题的并行计算

多核CPU 和多核GPU 的出现，使“分而治之”的并行处理思想获得硬件上的支持，随着处理器核心的不断扩展与成熟，并行系统已经开始成为主流。CUDA 是利用GPU 进行科学计算的全新并行计算体系架构，成为并行计算的一种实现模式，其主机、GPU 数据之间的传递关系如图3所示［10］。

图3 并行计算数据传递Fig.3 Data transfer of parallel computing

在接触碰撞问题的处理上，除了一般的有限元分析步骤，还增加了接触的搜索和接触力的计算两个过程。此外，结构的质量矩阵采用集中质量矩阵形式，这就使得运动微分方程得以解耦，简化方程组的求解。其有限元计算的主要步骤如下。

（1）输入相关参数并计算集中质量矩阵。

（2）时间历程的循环：①节点内力的计算；②接触搜索并计算接触力；③根据运动微分方程求解每一迭代步的运动状态；④根据需要输出中间结果。

（3）结果的后处理。

瞬态分析采用的积分步长一般较小，完成瞬态分析过程需要较长的时间，因此第2步是并行计算的主要步骤［11］。在这个步骤中，并行计算要完成节点力、接触力的搜索和计算，由于主机和设备之间数据的传输耗时取决于PCI-E 接口的带宽，因此这一步要尽量减少主机和设备的数据传输。

在有限元计算中，接触碰撞问题并行计算步骤如下。

1）质量矩阵和刚度矩阵的并行生成

采用CUDA 提供的原子函数atomicAdd（），其函数原型为：

unsigned long long int atomicAdd

（unsigned long long int＊address，unsigned long long int val）；

从函数原型中可以看到，atomicAdd（）只能进行整形数据的操作，由于计算能力支持64位数据的操作，因此可以先将质量矩阵的元素乘以一个大数（相乘之后的数值不能超过263-1），然后在完成质量矩阵的叠加之后除以这个大数。质量矩阵采用集中质量矩阵形式，按照单元数目为并行计算配置线程，一个线程控制一个单元，在每个单元内进行相关计算。在完成各个单元计算之后，要按照单元和节点对质量矩阵进行叠加。由于各个线程并行执行，在质量矩阵的叠加过程中会发生线程冲突，使矩阵在相应的叠加位置上只计入最后一个线程所计算的数值，这就要调用CUDA 的原子函数atomicAdd（）对叠加计算进行处理。其函数原型为：

int atomicAdd（int＊address，int val）；

unsigned int atomicAdd（unsigned int＊address，unsigned int val）；

unsigned long long int atomicAdd（unsigned long long int＊address，unsigned long long int val）；

从上面的函数原型可以看到，atomicAdd（）不支持双精度浮点数。为了有效利用这一函数，可以将质量矩阵的元素同时乘以较大的数值，所乘的数值一方面要满足计算的精度，另一方面要保证最后的计算数值不超过263，这一数值是由unsigned long long int所占的字节数决定的。在叠加完成之后，再将各个矩阵元素除以这个大数。由于刚度矩阵的某些元素值较大，在采用原子函数进行操作时会产生较大的误差，因此刚度矩阵只能按照上述方式生成。

为了减少数据在主机和设备端的传输耗时，质量矩阵和刚度矩阵应直接在设备端产生。由于系统只需要一次性生成质量矩阵和刚度矩阵，因此该过程的耗时在整个瞬态分析中占的比重较小，如果分析的时间较长，也可以直接在CPU 端生成刚度矩阵，然后再将数据传输到GPU 端。

2）节点内力的并行计算

在涉及几何非线性的接触碰撞问题中，节点内力fe计算公式［12］如下。

式中：几何矩阵可分解为B0和BL两部分，即

式中：B0是几何矩阵中与单元节点位移无关的部分；BL是与单元节点位移相关的部分。

3）接触搜索和接触力的计算

接触搜索的并行计算主要集中在全局搜索的过程中，而局部搜索主要是计算接触间隙并确定接触力的过程。在主从接触面算法中，首先要指定主接触面和从接触面，然后按照节点数目配置线程。所有线程并行搜索与该线程对应的主击节点的最近从节点，找出包含该从节点的距离主击节点最近的靶单元面。形成接触测试对后，计算主击节点与靶单元面的距离，判断接触状态并计算接触力。

4）数据的传输

主机和设备数据的传输速率取决于PCI-E 的带宽，PCI Express 2.0×16专门为显卡设计，理想的传输速率为10Gbyte／s，而PCI Express 3.0 的设计带宽为20Gbyte／s。但是，在有限元计算中，前后端的数据量很大。为了尽可能地减少数据传输耗时，一方面，将中间数据直接在显卡中产生；另一方面，只输出特定节点的运动状态，并且在输出选定节点运动状态时间隔一定时间步长来传输。

4 算例分析

4.1 气囊模型缓冲性能的仿真验证

气囊缓冲是航天器着陆缓冲的重要方式之一，如图4所示。简单气囊模型的负载施加6m／s的初速度，振动响应点为负载的中心点。上部负载和下部地面均为刚性体，为四边形的壳单元，其中负载总质量为50kg。气囊为三角形膜单元，1／4的尺寸坐标可由式（6）计算，厚度为0.254 mm，弹性模量为6GPa，泊松比为0.33，密度为875kg／m3。

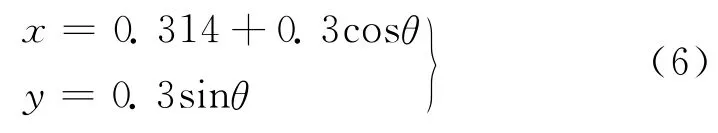
式中：线性坐标x和y的单位为m；θ为角度，0≤θ≤60°。

算例仿真的程序运行在同一平台，在计算分析过程中没有其他软件的干扰。计算仿真过程的计算机硬件平台如下。

由图5～7的计算仿真结果可以看出，采用分析方法的串行计算程序和并行计算程序计算结果，与MSC.Dytran的计算结果一致，表明分析计算程序的正确性和可靠性。计算分析误差首先来源于选取单元的类型和合理性，算例分析采用的是壳单元（Shell），而MSC.Dytran分析采用的是三角元（Tria3）等参元；另外，第2积分步长的选取也会产生计算分析结果的差异。

表1对比了本算例串行计算和并行计算的计算效率。结果表明：并行计算对串行计算的加速倍数，随着自由度数的增加而不断提高，提高的倍数会不断趋近于一个峰值。

图4 气囊模型Fig.4 Airbag model

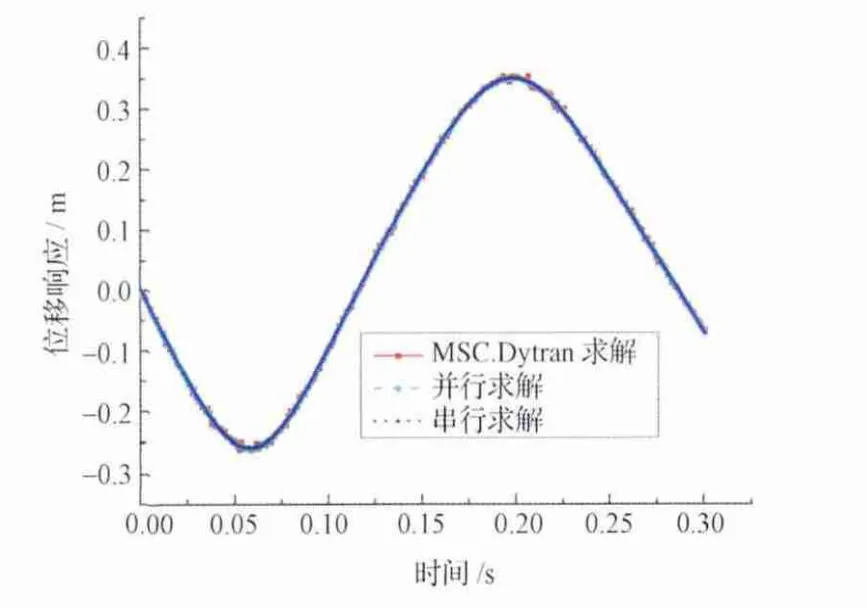
图5 气囊回收物重心处的位移响应曲线Fig.5 Displacement response curve of airbag recovery body center of gravity

图6 气囊回收物重心处的速度响应曲线Fig.6 Velocity response curve of airbag recovery body center of gravity

图7 气囊回收物重心处的加速度响应曲线Fig.7 Acceleration response curve of airbag recovery body center of gravity

表1 瞬态分析计算效率Table 1 Computation efficiency of transient analysis

4.2 典型圆柱筒接触碰撞瞬态分析

月球软着陆支架的主腿为一端开口的圆柱结构，如图8所示。结构仍然采用三角形单元离散，其底部直径为0.2 m，高度为1 m。材料的弹性模量为70GPa，泊松比为0.3，密度为2800kg／m3。假设该圆柱筒以10m／s的速度沿着垂直地面的方向与某一刚性墙相撞，计算结果如图9～11所示。

由图9～11可以看出：利用本文的串行算法和并行算法计算得到的薄壁筒上缘某节点的位移和速度响应曲线，基本与MSC.Dytran 的吻合，加速度响应曲线略有差别。产生差别的部分原因，与第4.1节一般瞬态分析问题一致；此外，还因为采用的接触搜索算法和接触力的计算方法不尽相同，加之MSC.Dytran采用变积分步长来进行数值积分。不过，利用本文算法计算的结果基本反映了接触碰撞的规律，具备一定的可靠性。

在比较并行计算的加速倍数时，以10个迭代步的计算时间为比较标准，计算时间和加速倍数见表2。由于接触碰撞涉及到非线性计算，每一个迭代步的节点内力都要在更新位形后进行计算，这与线性计算中提前生成刚度矩阵，然后利用刚度矩阵计算节点内力的方式不同。从表2可以看出：接触碰撞并行计算的加速倍数峰值约为5.70；在2000个自由度以内，加速倍数基本线性增长；当自由度在2000～5000范围时，加速倍数基本进入峰值阶段。由于主体的分析计算基本上为一个线性叠加的过程，没有涉及较为复杂的计算过程，因此，随着自由度的继续增加，并行计算的加速倍数基本维持在峰值附近。

图8 典型一端开口的圆柱筒Fig.8 Typical cylinder with open end

图9 薄壁筒上缘节点的位移响应曲线Fig.9 Displacement response curve of edge node on thin wall cylinder

图10 薄壁筒上缘节点的速度响应曲线Fig.10 Velocity response curve of edge node on thin wall cylinder

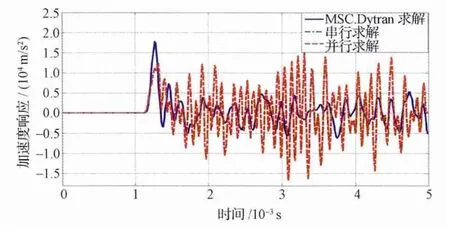
图11 薄壁筒上缘节点的加速度响应曲线Fig.11 Acceleration response curve of edge node on thin wall cylinder

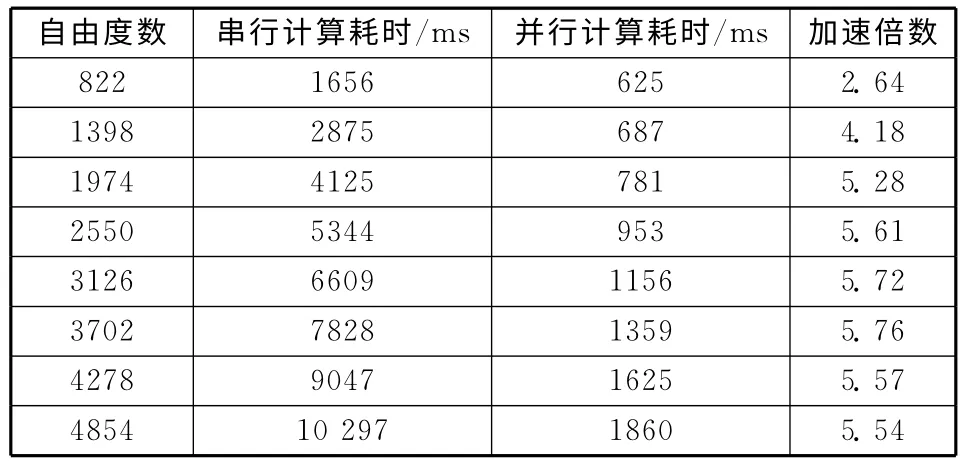
表2 接触碰撞的计算效率Table 2 Computation efficiency of contact impact

5 结论

（1）航天器着陆碰撞过程极为复杂，并行算法可有效提高碰撞仿真计算效率，实现航天器着陆过程中动力学计算的快速和高精度，并解决航天器着陆碰撞瞬态分析的长耗时、费资源等问题。

（2）本文将CUDA 并行计算技术应用到线性瞬态分析问题的显式求解上，研究了质量矩阵和刚度矩阵的并行生成方法，并将基于中心差分法的求解过程并行化实施。算例表明，本文算法具有较高的可靠性，并行计算效率随着自由度数的增加而不断提高。

（References）

［1］Belytschko T，Neal M O.Contact-impact by the pinball algorithm with Penalty and Langrangian methods［J］.International Journal for Numerical Methods in Engineering，1991，31（3）：547-572

［2］Malone J G，Johnson N L.A parallel finite-element contact-impact algorithm for nonlinear explicit transient analysis，part 1：the search algorithm and contact mechanics［J］.International Journal for Numerical Methods in Engineering，1994，37（4）：559-590

［3］Zhong Z H，Nilsson L.Contact-impact algorithm on parallel computers［J］.Nuclear Engineering and Design，1994，150（2／3）：253-263

［4］Attaway S W，Hendrickson B A，Plimpton S J，et al.Parallel contact detection algorithm for transient solid dynamics simulations using PRONTO3D［J］.Computational Mechanies，1998，22（2）：143-159

［5］Noor A K，Lambiotte J J.Finite element dynamics analysis on CDC Star 100computer［J］.Computers ＆Structures，1979，10（1）：7-19

［6］Ou Ronfu，Fulton E.An investigation of parallel numerical integration methods for nonlinear dynamics［J］.Computers ＆Structures，1988，30（1）：403-409

［7］余天堂.一种求解结构动力响应的并行解法［J］.河海大学学报（自然科学版），1999，27（3）：75-78 Yu Tiantang.A parallel solution of dynamic response of structure［J］.Journal of Hohai University （Natural Sciences），1999，27（3）：75-78（in Chinese）

［8］Hajjar J F，Abel J F.Parallel processing of central difference transient analysis for three-dimensional nonlinear framed structures ［J］. Communications in Applied Numerical Methods，1989，5（1）：39-46

［9］Chiang K N，Fulton R E.Structural dynamics methods for concurrent processing computers［J］.Computers ＆Structures，1990，36（6）：1031-1037

［10］NVIDIA Corporation.NVIDIA＿CUDA＿Programming Guide＿2.3 ［Z／OL］.（2009-07-01）.［2013-09-02］.http：／／www.nvidia.cn／object／cuda＿develop＿cn.html

［11］金先龙，李渊印.结构动力学并行计算方法及应用［M］.北京：国防工业出版社，2008 Jin Xianlong，Li Yuanyin.The parallel algorithm and its application for structure dynamics［M］.Beijing：National Defense Industry Press，2008（in Chinese）

［12］温文源.机械结构计算的有限元法［M］.南京：东南大学出版社，1989 Wen Wenyuan.Finite element method for mechanical structure［M］.Nanjing：Southeast University Press，1989（in Chinese）