关中Q2黄土流变特性及宏观流变试验研究*
2014-12-26徐增伟
赵 敏,徐增伟
(西安工业大学 建筑工程学院,西安710021)
黄土滑坡的发生、高速公路的路基沉陷、湿陷性黄土地基桩的负摩擦力问题、黄土地区挡土墙后土压力的变化和深基坑开挖过程中坑壁的稳定性等与时间有关,开展时间因素对黄土的力学特性、应力应变关系影响的研究,对于推动黄土力学的进一步发展,指导黄土地区各类岩土工程的设计、施工和进行稳定性分析,保证结构物的长期安全和正常使用等方面,具有重要的理论和实践意义.
20世纪50年代,荷兰的Geuze和国内学者陈宗基对土流变问题进行了系统研究,陈宗基[1]从宏观和微观两个方面提出了粘土的流变本构方程,二次时间效应及片架结构理论;对于黄土微观流变试验而言,高国瑞、雷祥义[2-6]等认为黄土的流变性质取决于它的结构特征,而结构的强弱又取决于连接颗粒之间键的强弱,键的强弱与颗粒间的距离、相对位置、生成历史以及外在环境等复杂因素有关.影响土流变性质的因素是多方面的,包括应力、围压、颗粒组成、应力历史和应力路径、温度、含水率等,这些因素关系到水分与粒间联系的相互作用,还关系到一定应力状态下黄土矿物颗粒晶体内部的变化;黄土流变过程的发生与发展,就是这些物理、化学、力学等因素共同作用的结果.关于黄土流变的研究还有很多不足,对于其在长时间范围内的变化规律还有待研究,建立的数学模型还有待完善,为此本文根据黄土流变模型构建并结合宏观流变试验分析了关中Q2黄土在不同压应力和含水量下的变形规律,以期得到关中Q2黄土的流变特性规律.
1 黄土流变模型的建立
岩土流变模型把土的流变特性看成是弹性、粘滞性和塑性共同作用的结果,其中土的弹性用符合虎克定律的弹性元件模拟,土的粘滞性用符合理想牛顿体规律的粘壶模型模拟,土的塑性用摩擦元件模拟,摩擦元件服从圣维南定律;三种基本流变元件可以分别以串联或并联的方式组合成不同的模型,不同的组合模型可以描述材料的不同特性.传统模型只适合描述岩土材料的衰减蠕变和等速蠕变.为了完整描述岩土材料的真实流变过程,文中模型构建分为线性流变建模与非线性流变建模[7].
1.1 线性流变建模
线性流变研究的主要问题是物体的本构关系,即应力、应变之间的关系,在不同的时刻是不同的,但在同一时刻,本构关系仍然是线性的,反映在应变速率与应力的关系图是一组直线或折线;当应力水平为定值时,对于粘弹塑性流变材料,其蠕变方程及其蠕变速率方程表示为

式中:ζve(t)为粘弹性蠕变柔量;ζvp(t)为粘塑性蠕变柔量;ηve(t)为粘弹性粘滞系数;ηvp(t)粘塑性粘滞系数.
只能描述岩土蠕变的前两个阶段,不能描述岩土材料的加速蠕变.只要基本元件是线性的,最终模型所反映的总是线性粘弹性、粘塑性性质,它也只能描述蠕变的衰减蠕变和等速蠕变阶段,无法描述加速蠕变阶段.
1.2 非线性流变建模
当考虑弹性元件的非线性应力应变关系和牛顿元件的非牛顿体的特性时,可以描述材料的的非线性流变特性和不稳定蠕变特性,即可以研究岩土材料的加速蠕变现象.非线性流变的应力应变关系在同一时刻是非线性的,反应在应力应变关系图上就是不同时刻下的每条应力应变等时曲线不再是直线或者折线,而是一簇曲线,图1为同一坐标系中土的等时曲线和蠕变曲线[8-10].

图1 土的等时曲线与蠕变曲线Fig.1 Soil tautochrone and creep curve
由图1可知,随时间的推移,粘性变形的发展导致应力应变等时曲线越向应变轴靠拢.应力水平越高,应力应变等时曲线偏离直线的程度也越大,说明非线性程度随应力水平的提高而增强.另外,随着时间增长,应力应变等时曲线偏离直线的程度增加,说明非线性程度亦随时间的增长而增强.
式(1)为线性流变的蠕变方程,其蠕变柔量仅是时间函数,与应力水平无关;而非线性流变的蠕变柔量不仅是时间函数,还与应力水平有关,即将式(1)经过变化即可得到非线性流变的蠕变方程为

2 宏观流变试验
2.1 试验方法
以关中地区渭河流域第四纪湿陷性黄土为主要试验对象,考察黄土在不同含水量和压缩压力下的流变特性.试验所用土样的基本物理力学指标见表1,试验历时2个月.
采用水膜迁移法对土体进行人工增湿,分别配备含水 量 为 10%,15%,20%,25%,30%,35% 的试验土样,根据土样的实际含水量及其预定目标含水量,采用式(4)计算需要增加的水的质量.

式中:mw为所需加水的质量;ω为所配土样含水率;ω0为初始土样含水量;m0为初始土样质量.

表1 土体基本参数Tab.1 Basic parameters of soil masses
试验所用仪器为CSS-2901TS型土体三轴流变试验机,该试验机主要用于土体在单轴尤其是三轴应力作用下的流变性能测试.试验机由主机、轴向力测量系统、轴向变形测量系统、孔隙压力测量系统、孔隙水流量测量系统、轴向控制系统、围压控制系统、计算机系统等组成.计算机能够自动对测量的数据进行实时处理,同步生成ε~t、σ~t、ε~lgt等曲线,并将数据处理结果与设定的试验结束条件进行实时动态对比,以确定是否满足结束试验的条件.为保护试验设备,试验负荷或变形超过设定值的120%,当试验力值超量程时,或试样破断时,均能自动停车,并发出相应灯光信号,同时保存最后试验结果.
试验内容:第1组为不同压应力下的黄土流变试验,4个试样进行的是固定含水率为20%条件单级加载流变试验;第2组为不同含水率下的黄土流变试验,6个试样的含水量分别为10%,15%,20%,25%,30%,35%,两组试样在进行流变试验之前进行充分固结.
2.2 结果与分析
2.2.1 不同压应力下的黄土流变试验
流变试验采用单试样单级加载方式进行,试样含水率为20%,试验围压300kPa;按照Boltzmann线性叠加原理对4个黄土试样大量的试验数据进行处理可得到的Q2黄土常规三轴流变曲线如图2所示.
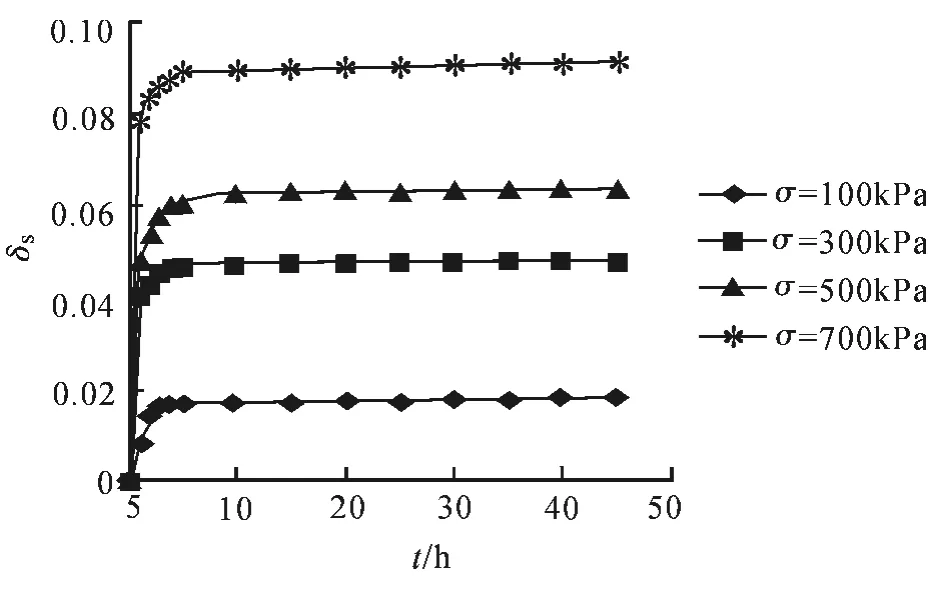
图2 不同压应力下Q2黄土三轴流变试验曲线Fig.2 Triaxial rheological test curve of Q2loess under different stress
从图2可以看出流变曲线有以下特征:① 曲线分为两段,第一段为呈对数函数的线减速阶段,即不稳定湿陷阶段,第二段可认为是线性变形阶段,流变速率为一接近零的常数;② 加载初期,各级荷载下都产生了相当大的瞬时变形;③ 变形总体趋势大致相同,均表现为荷载持续约5h后,不管应力水平高低,流变曲线都呈稳定流变,40h后,流变变形量与所持续时程相比几乎不变;④ 在高应力作用下流变速率明显加快,该阶段持续时间与低应力状态下相差不大.
第一阶段的变形是由水分与内部联系相互作用引起的结构不可逆现象造成的,具体表现在土体内部架空结构的逐渐破坏,这一阶段的变形仅具有塑性的本质.第二阶段的变形是由逐渐衰减的粘塑性流造成的,这种粘塑性流是由土粒矿物晶体内部的物理化学过程引起的,该阶段中流变过程虽有接近于零的趋势但并未停止,经过一定时间后,流速与过程持续时间相比变化不大,可认为流速是不变的.第一阶段的持续时间远小于第二阶段,各阶段的作用大小与荷载、含水量、黄土性质等有关[11-12].
同一含水率下随着压应力的增加,曲线的初始斜率依次增大,这与黄土的内部结构有关,黄土内部架空结构层所能承担的荷载不同,在低压力状态下,大部分结构拥有足够的强度抵抗外部压力,而当压力超过某一架空结构层所能承受的荷载时,就会突然破坏.
2.2.2 不同含水率下的黄土液态试验
图3为固定压力(σ=300kPa)和不同含水量下土的湿陷系数随时间变化的蠕变曲线.从图3可以看出,土的变形量和发展速度是随含水量的增加而增加的,即在相同的荷载下,含水量越高,完成等量变形所需的时间越短.

图3 不同含水率下Q2黄土三轴流变试验曲线Fig.3 Triaxial rheological test curve of Q2 loess under different water content
随着其成分和状态的不同,黄土湿陷时有可能产生长期塑性变形而不破坏其结构的连续性[11].因为长期塑性变形能使建筑物丧失整体稳定,所以在建筑物地基中,土的长期塑性变形是不容许的.土的塑性变形是稳定蠕变阶段发展的结果,在所有的情况下,湿陷性黄土的强度都可以用变形转入蠕变阶段的转变点来表示.土的含水量对湿陷过程的影响可以用像温度对连续物体蠕变的影响来解释,即塑性变形与因含水量变化所引起的土的某些结构单元的运动有关,在给定一时刻,每个结构单元都具有一定的能量,而且各单元间的能量分布服从马克韦尔定律.
与图2一样,随含水率的增加曲线的初始斜率也在增加,这与黄土的特殊化学成分有关.总之,无论是传统的溶盐假说还是新兴的结构学说,水在黄土的变形研究中都扮演着重要角色,水的参与赋予黄土特殊的性质,一定范围内,含水量的增加促进了水溶盐的溶解,更改了原本的架空结构体系,因而具有更大的变形量.
含水量对湿陷性黄土中发生长期变形的影响,可以根据水分与矿物颗粒晶格的相互作用机理来解释.组成湿陷性黄土的矿物团粒拥有活性晶格,在适当的条件下,它能把水分子吸入晶体内部,从而产生塑性变形.土的矿物颗粒及其团粒体的崩解过程能够在力场中发生,力场展开在带电土颗粒之间,由于胶粒分子对水分子的吸附作用,把水分和吸附离子吸附在土粒周围.水分是土的“减硬剂”,它给土以塑化作用,促成了流变过程的发展.
图4为不同含水量下土的湿陷值与压应力的关系曲线,证明湿陷时土的变形具有曲线规律.图4的曲线画在图5的对数坐标上成为直线,证明土湿陷时幂变形规律的正确性:δs=βσm,其中β为由压缩试验确定的黄土在压缩荷载广大变化范围内浸水时的变形参数,相当于黄土总变形模量的倒数,对于粗略计算来说,可以根据压缩试验的成果计算湿陷性黄土的变形参数[13],表达式为

式中:σ1、σ2为压缩荷载;lnδsσ1、lnδsσ2分别为与σ1、σ2相对应的土的湿陷值.

图4 不同含水量下土的湿陷值与压应力关系曲线Fig.4 Curve of collapsible value and stress under different water content
用图4的曲线族可以确定所给湿陷性黄土不同含水量下的“湿陷起点值”.如果认为土的相对变形达到1%属于湿陷的范围,那么用这个变形值画一条水平线与各条δs-σ关系曲线相交,各交点的横坐标就是响应含水量下土的“湿陷起点”值[11].

图5 不同含水率下Q2黄土三轴流变对数曲线Fig.5 Triaxial creep logarithmic curve of Q2 loess under different moisture
根据图4画出了土的“湿陷起点”随含水量变化的曲线如图6所示.由图6可以看出,随着含水量的增加,黄土的蠕变强度逐渐降低.这是由于黄土的强度基本上是由碳酸钙和硫酸钙造成的,这些盐类的胶结膜包裹土粒,在土中形成固化凝聚力;土粒及其团粒间固化凝聚力的抗水性较差,因此在水分作用下凝聚力大幅降低,为土结构各部分的彼此脱离创造了条件,当含水量增加时,黄土的强度因结构破坏而急剧降低,所以在压缩荷载下,黄土具有强烈被压缩的性质.

图6 土的湿陷起点随含水率变化的曲线Fig.6 Curve of collapsible point change with moisture
2.2.3 分时叠加流变曲线数学模型的推导
对于所有被研究的含水量值,由试验所得的蠕变曲线在很大的时间范围内是彼此相似的,因此δs(t)的全部曲线族可以用其中一族曲线将其纵坐标乘以某个量值(压应力的函数)而得到.在土中应力和含水量不变的条件下能引起变形随时间而发展的物理化学过程,与其相关的湿陷现象可以归入不平衡的流变之列.根据拉保特诺夫提出的时效理论可以假设湿陷性黄土在不变含水量条件下的变形、应力和时间之间存在着Φ(δs,σ,t)=0的固定关系,那么湿陷随应力和时间变化的关系式可以用两个函数的乘积表示为

式中:φ(σ)和ψ(t)分别为仅由应力和时间决定的函数.
黄土湿陷时的流变特性与含水率和所处应力状态密切相关,只有一定压力值而未知含水量时,不能确定是否会发生湿陷,只有当作用于土层的压力值与一定含水量值相适应时,才能发生湿陷变形.经试验关中地区黄土湿陷时的蠕变特点表现为加载初期呈非线性变形,这一阶段持续时间很短,而后期则表现为明显的线性变形.在确定变形与时间的数学模型时,建议分时间段叠加构建,同时考虑含水率、土性参数、所施加应力等因素,而含水率又与黄土的土性参数密切相关,其c、φ值在不同含水率下变化范围很大,即使在同一含水率下,湿陷不同阶段c、φ值也有较大差异,因而为简化模型,以含水率代表土性参数对流变特性的影响是有必要的,但此仅对同一种类黄土有效.考虑含水率和所施加应力的分时叠加黄土湿陷流变方程可表示为

式中:Γ1(ω)φ1(σ)ψ1(t1)为第一阶段非稳定流变函数;Γ2(ω)φ2(σ)ψ2(t2)为稳定流变线性函数.
3 结 论
1)不同压应力下Q2黄土流变曲线呈两阶段变化,第一阶段为对数减速变形阶段,主要由土体内部架空结构的逐渐破坏引起,第二阶段为稳定线性变形阶段,由逐渐衰减的粘塑性流造成.
2)不同含水率下Q2黄土土的变形量和发展速度随含水量的增加而增加,即在相同的荷载下,含水量越高,完成等量变形所需的时间越短,这与黄土的特殊化学成分有关,水的参与改变了土的物理化学性质,促进了流变过程的发展.
3)加载应力与含水率对流变的影响呈正相关,曲线变形趋势一致.
4)根据黄土流变呈两阶段变形的试验结果,考虑含水率和所施加应力对黄土流变的影响,得出黄土分时叠加流变模型.
[1] CHEN Z J.Structure Mechanics of Clay[J].China Science,1959,8(1):41.
[2] 高国瑞.兰州黄土显微结构和湿陷机理探讨[J].兰州大学学报,1979(2):123.GAO Guo-rui.Study of the Microstructures and the Collapse Mechanism in Loess Soil from Lanzhou[J].Journal of Lanzhou University,1979(2):123.(in Chinese)
[3] TIMP P,IAN S.Catastrophe Theory and Its Application[M].New York:Mc Graw Hill,l978.
[4] 王旭东,付小敏.压缩蠕变力学试验的数值模拟研究[J].工程地质学报,2009,17(4):533.WANG Xu-dong,FU Xiao-min.Numerical Simulation Test for Physical Compression Creep Experiment[J].Journal of Engineering Geology,2009,17 (4):533.(in Chinese)
[5] 孙钧.岩土材料流变及其工程应用[M].北京:中国建筑工业出版社,1999.SUN Jun.The Study on Rheology of Rock and Soil Materials and Its Engineering Application[M].Beijing:China Architecture &Building Press,1999.(in Chinese)
[6] 孔令伟,张先伟,郭爱国,等.湛江强结构性黏土的三轴排水蠕变特征[J].岩石力学与工程学报,2011,30 (2):365.KONG Ling-wei,ZHANG Xian-wei,GUO Ai-guo,et al.Creep Behavior of Zhanjiang Strong Structured Clay by Drained Triaxial Test[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(2):365.(in Chinese)
[7] 刘雄.岩土流变学概论[M].北京:地质出版社,1994.LIU Xiong.Introduction to Rock Rheology[M].Beijing:Geological Publishing House,1994.(in Chinese)
[8] 马莉英,肖树芳,王清.黄土的流变特性模拟与研究[J].实验力学,2004,19(2):178.MA Li-ying,XIAO Shu-fang,WANG Qing.Simulation and Study on Rheological Behavior of Loess[J].Journal of Experimental Mechanics,2004,19(2):178.(in Chinese)
[9] 赵玲,葛科,刘恩龙.黄土的流变特性分析[J].建筑科学,2011,27(3):69.ZHAO Ling,GE Ke,LIU En-long.Study on the Rheological Properties of Loess[J].Building Science,2011,27(3):69.(in Chinese)
[10] 谢星,王东红,赵法锁.Q2黄土流变特性及其统计损伤流 变 模 型 [J].水 文 地 质 工 程 地 质,2010,37(3):63.XIE Xing,WANG Dong-hong,ZHAO Fa-suo.Study on Rheological Properties and Statistical Damage Rheological Model for Q2Loess[J].Hydrogeology& Engineering Geology,2010,37(3):63.(in Chinese)
[11] 郭增玉,冯同新.高湿度Q2黄土的试验流变特性[J].地下水,2004,26(1):70.GUO Zeng-yu,FENG Tong-xin.Test of Rheologic Characteristics of Q2Loess with High Humidity[J].Ground Water,2004,26(1):70.(in Chinese)
[12] 张军辉,缪林昌.连云港海相软土流变特性试验及双屈服面流变模型[J].岩土力学,2005,26(1):145.ZHANG Jun-hui,MIAO Lin-chang.Tests on Rheological Behavior of Lianyungang Marine Soft Clay and Two-Yield-Surface Rheological Model[J].Rock and Soil Mechanics,2005,26(1):145.(in Chinese)
[13] 谢星,赵法锁,王东红.西安地区Q2黄土非线性流变模型[J].长安大学学报:自然科学版,2009,29(5):41.XIE Xing,ZHAO Fa-suo,WANG Dong-hong.Nonlinear Rheological Model for Q2loess in Xi’an Region[J].Journal of Chang’an University:Natural Science Edition,2009,29(5):41.(in Chinese)
