基于统计线性化伴随法的导弹制导系统精度分析
2014-12-25彭绍雄王海涛安进邹强
彭绍雄,王海涛,安进,邹强
(1.海军航空工程学院飞行器工程系,山东烟台264001;2.海军航空工程学院研究生管理大队,山东烟台264001)
0 引言
对于导弹制导系统这种复杂的、具有多种随机输入的非线性时变系统[1],主要采用蒙特卡罗法(Monte-Carlo)进行精度分析。蒙特卡罗法的仿真精度与模拟计算的次数相关,需要耗费大量机时才能达到较高的精度,不适于大量的计算分析。随着伴随技术(AT)和协方差描述函数技术(CADET)的相继发展,大大简化了对具有随机输入的非线性时变系统的分析过程,提高了分析效率[2-3]。
由协方差描述函数法和伴随技术相结合构成了导弹制导系统完整的统计性能分析方法,即统计线性化伴随法(SLAM)。本文运用该方法对导弹制导系统在多种随机干扰因素作用下的制导精度进行分析,不仅可以得到与CADET分析一样的均方根散布,同时还集合了AT法的优点,能够提供各种干扰对总的均方根值的影响,更为全面地反映了导弹制导系统的统计性能。
1 统计线性化伴随法
导弹制导系统为非线性时变系统,其状态方程可表示为:
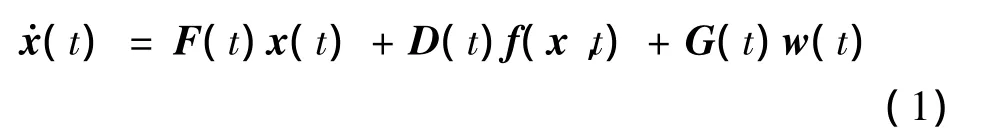
式中,x(t)为系统的状态向量;F(t)为状态矩阵;f(x,t)=[f1,f2,…,fn]T为非线性向量函数;G(t)为输入矩阵;w(t)为外部干扰,由一均值向量b(t)和一随机分量u(t)组成,且u(t)是具有谱密度Q(t)的白噪声过程。
1.1 系统协方差分析
运用描述函数理论将非线性向量函数f(x,t)进行统计线性化:
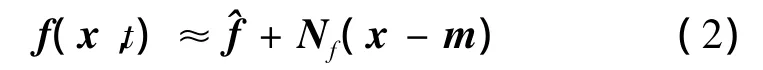
系统状态变量的均值和协方差传播方程为:
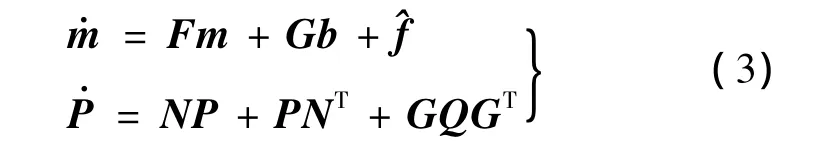
1.2 伴随系统的构建
由式(1)~式(3)可得:
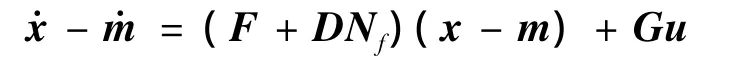
即
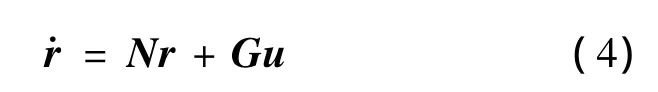
式中,r=x-m,r为系统状态向量的随机部分,为零均值的随机量。
系统的输出为y=Cr,于是得出SLAM模型为:
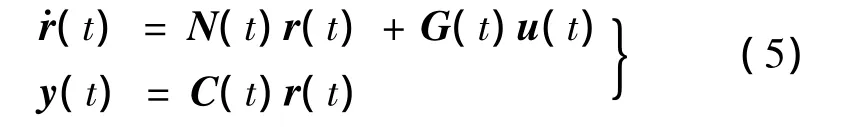
初始条件为 r(t0)=r0,0≤t≤tf。
根据伴随系统的形成规则,可得伴随系统为[4-5]:
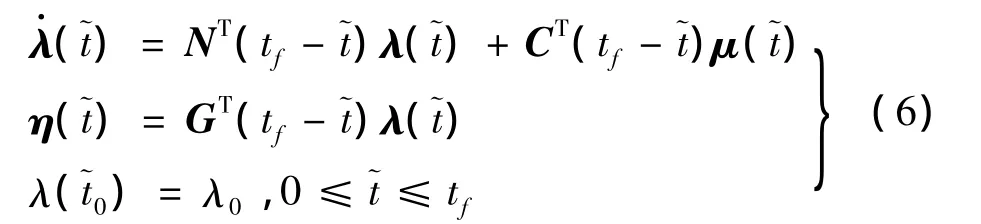
1.3 均方根计算
设系统的第i个白噪声输入信号为ui(t),根据文献[6]的推导,ui(t)引起的均方根散布表达式为:
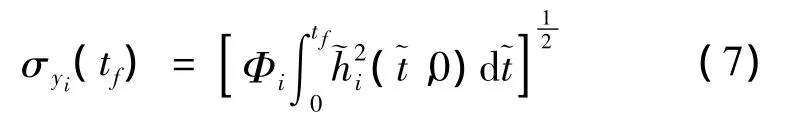
式中,Φi为ui(t)的谱密度。上式说明了均方根脱靶量与噪声功率谱密度的关系,也就给出了各个输入噪声对导弹脱靶量的影响。
由线性系统的叠加原理,系统输出y(tf)的总方根散布σy(tf)为:
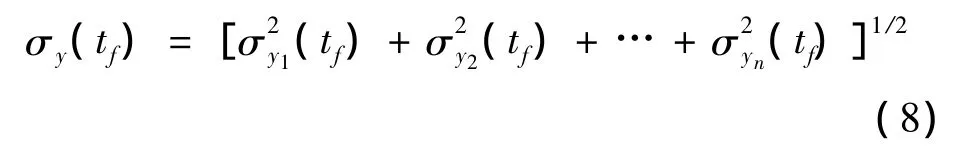
这样不仅得到了y(tf)的均方根散布,而且得到了均方根散布分量σyi(tf)。
2 制导系统数学模型
某导弹采用雷达导引头,制导系统包括导引头、自动驾驶仪、制导规律、目标机动及导弹目标运动学环节等,其相互关系如图1所示。
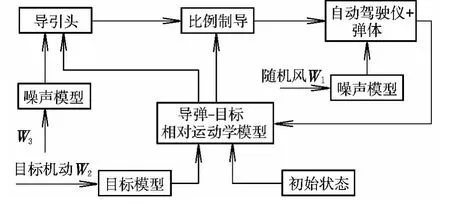
图1 导弹制导系统框图Fig.1 Diagram of missile guidance system
2.1 导引头模型
根据导引头的动态特性建立导引头模型,将导引头简化为一阶环节,输入输出关系为[7]:
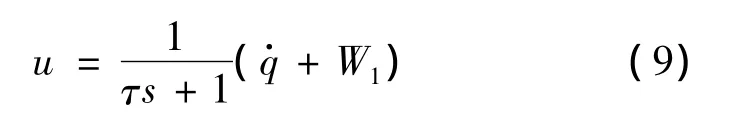
式中,u为导引头的输出信号;τ为导引头时间常数;W1为测角速度偏差,用高斯白噪声表示。
2.2 自动驾驶仪模型
导弹的加速度回路可简化为二阶系统,其数学模型为:

式中,TC为时间常数;ξC为阻尼系数;nC为指令过载;为无弹体过载限幅时弹体对控制指令的响应。须加以限制,限制过程用饱和非线性表示:
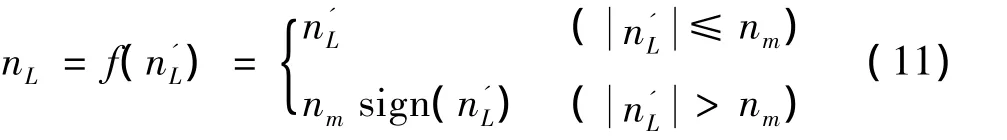
式中,nL为弹体实际过载;nm为导弹最大允许过载。
2.3 导弹、目标相对运动学模型
假设导弹、目标处于同一平面内运动,则导弹与目标的相对运动方程为:
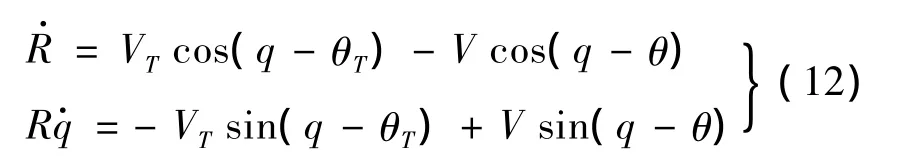
式中,R为导弹与目标的相对距离;q为目标视线角;V,VT分别为导弹与目标的速度;θ,θT分别为导弹和目标的速度航向角[8]。
2.4 目标运动模型
假设目标速度Vt为常值,横向加速度at是随机变化的,视为一阶马尔可夫过程,其传递函数为一阶低通滤波器,其功率谱密度函数为:
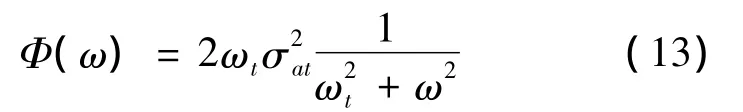
式中,σat为加速度均方根,反映目标的加速度水平;ωt为目标机动带宽。用白噪声模拟时,其传递函数为一阶低通滤波器
目标横向加速度用微分方程表示为[6]:
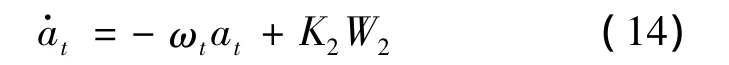
式中,W2为白噪声输入;ωt为目标机动带宽。
2.5 随机风模拟
鉴于风向变化的多样性,只考虑侧向阵风的影响。侧向阵风可以看作是由均值风和大气紊流组成。均值风不用模拟,侧向紊流采用Dryden大气紊流模型模拟,相应的传递函数为:
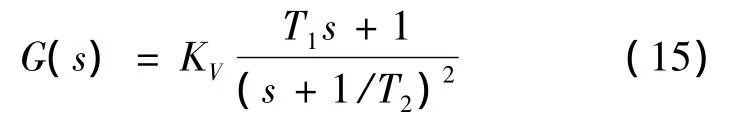
3 制导精度统计分析
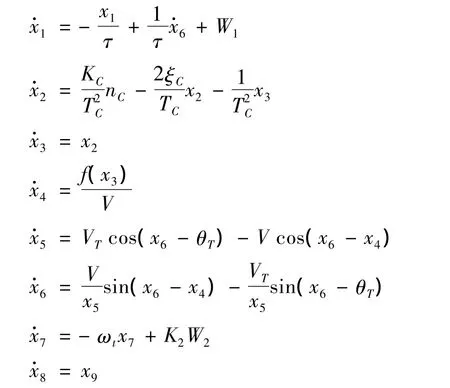

式中,nC=KVx1,nC为指令过载。分别取f1=f(x3),
将以上状态方程写成矢量形式为:
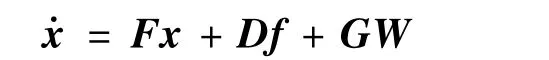
式中,F,D及G中大部分都是零元素,限于篇幅,不在此给出。对非线性函数f进行统计线性化,求出对应的描述函数和Nf。
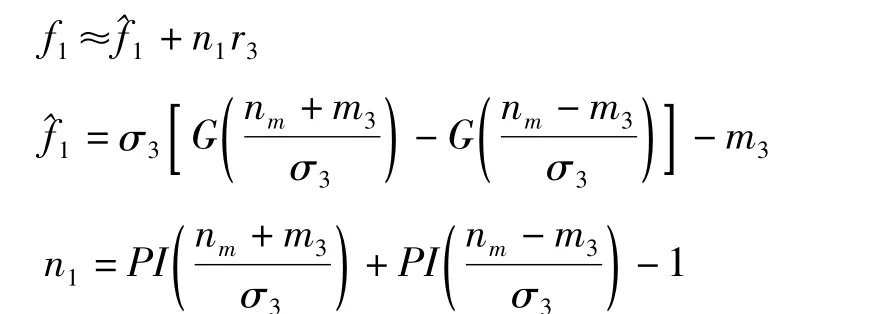
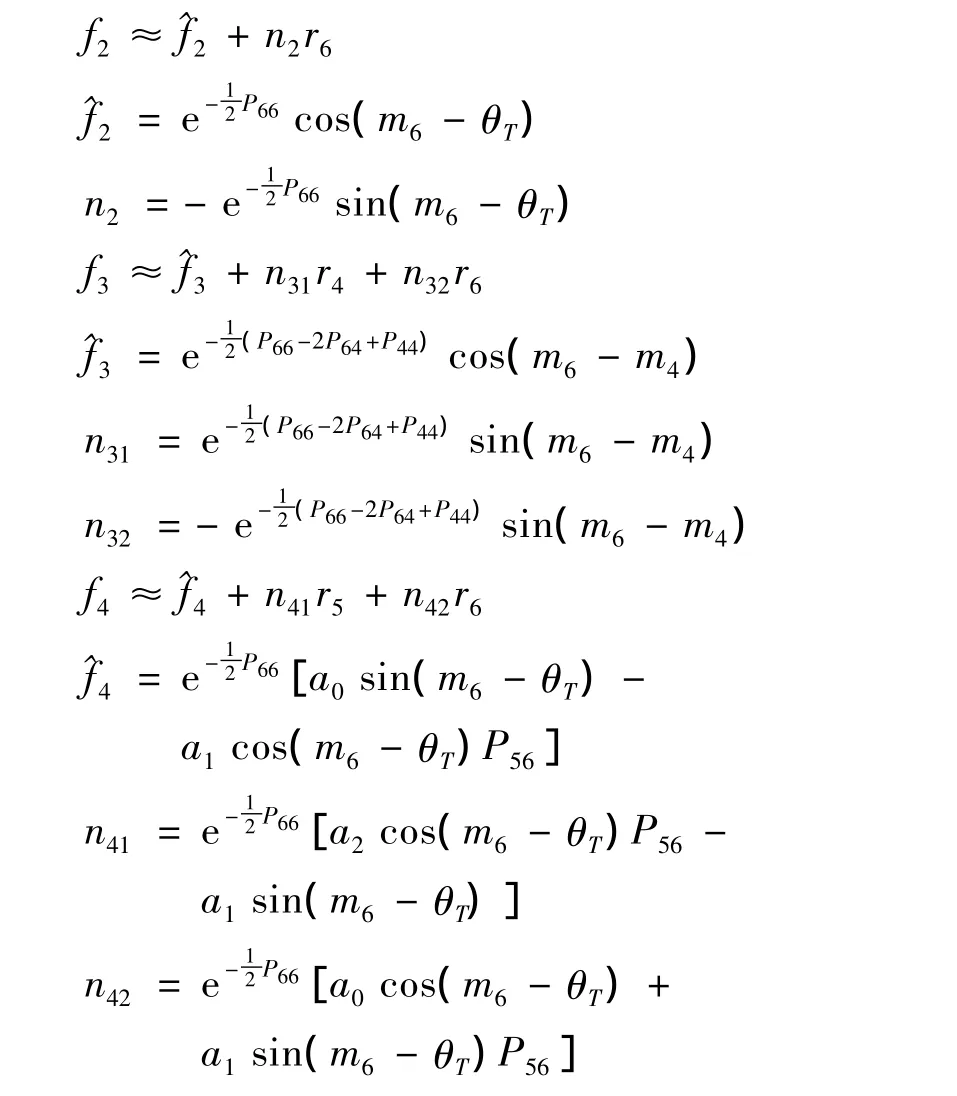
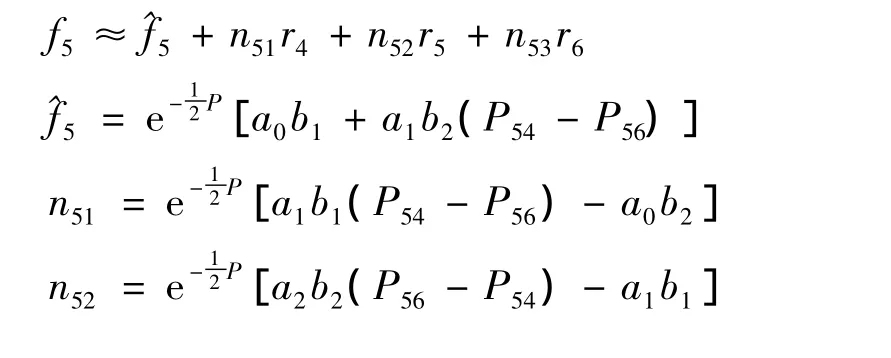
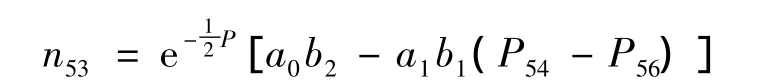
式中,P=P66-2P64+P44;b1=sin(m6-m4);b2=cos(m6-m4)。
由N=F+DNf,可得辅助矩阵N如下:
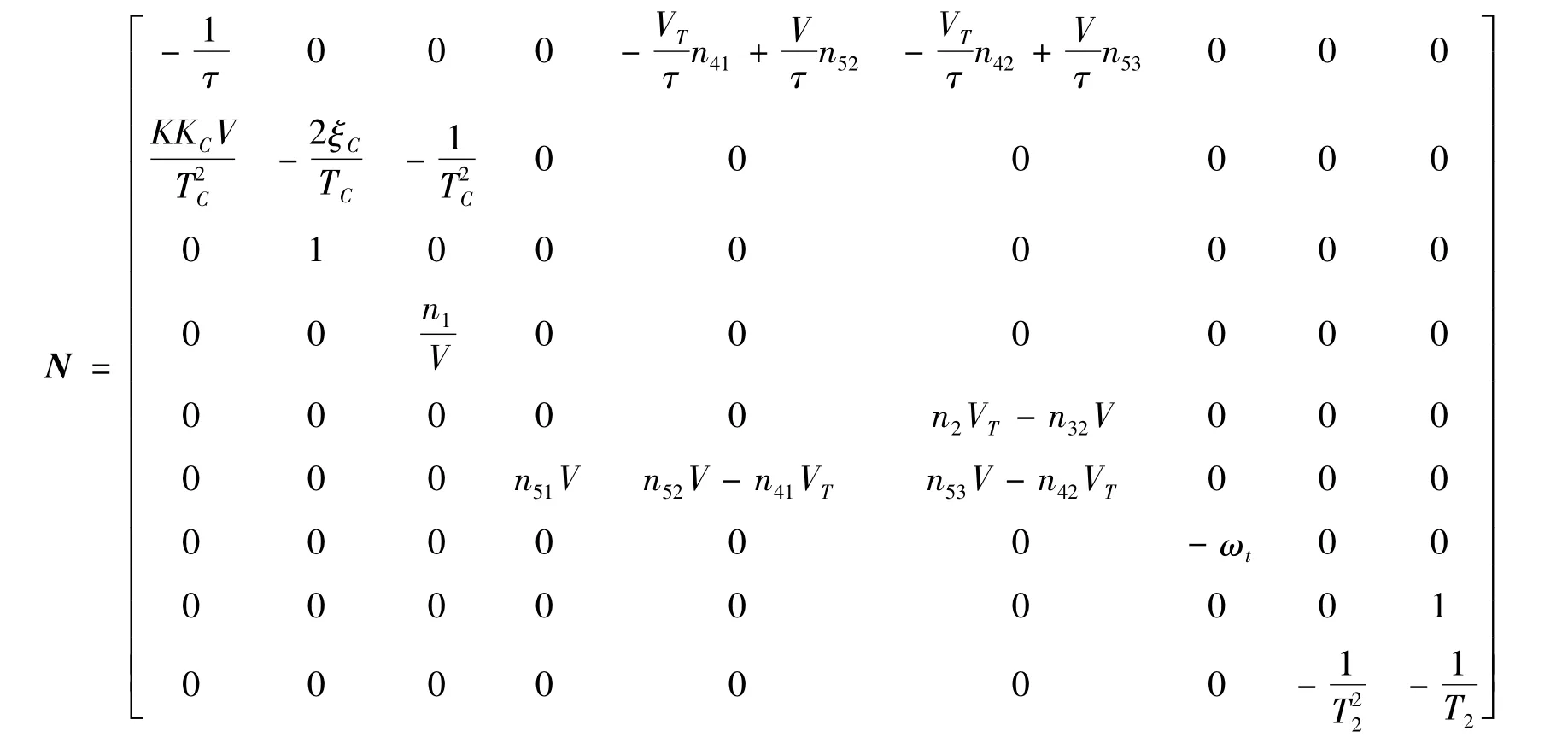

4 仿真结果及分析
已知导弹与目标的初始距离R=9 km,目标飞行速度VT=400 m/s,导弹的初始飞行速度V0=800 m/s,导引系数K=4。针对不同的随机干扰因素,仿真结果如图2~图5所示。
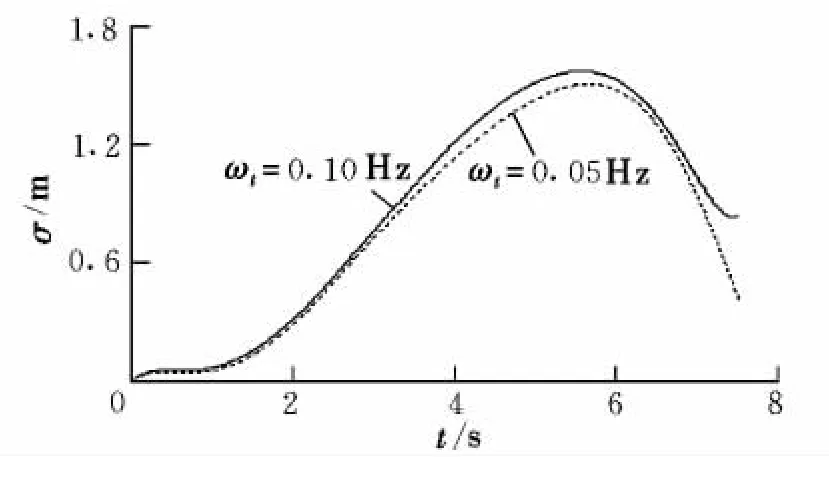
图2 目标机动对相对距离均方根的影响Fig.2 Effect of target maneuver on RMSof relative distance
由图2可知,相对距离均方根随导引时间的增加呈现先增大后减小的趋势。当目标机动带宽ωt=0.05 Hz时,7.5 s时的均方根值为0.415 m;当ωt增大至0.10 Hz时,相应的均方根值为0.837 m,表明目标机动带宽对相对距离均方根的影响比较显著。这是由于目标机动带宽增加引入高频分量,使得横向加速度随机波动性增大,直接导致脱靶量和均方根散布的增加[9]。
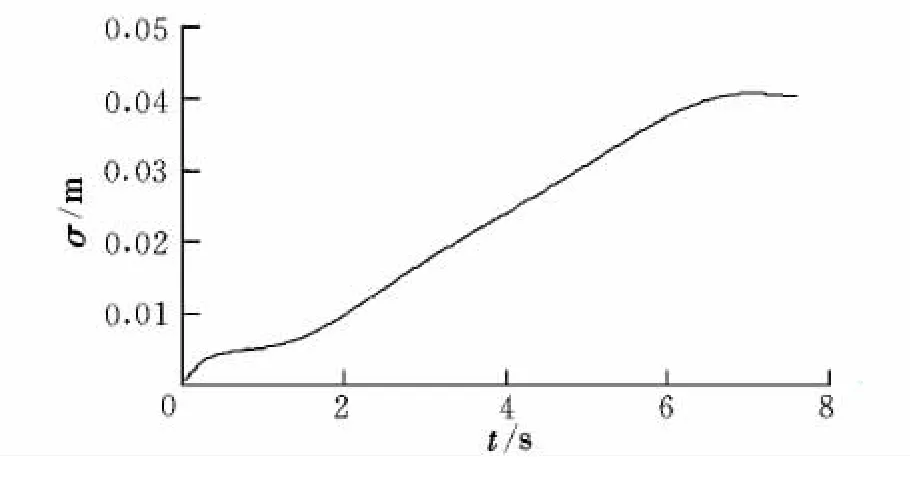
图3 随机风对相对距离均方根的影响Fig.3 Effect of random wind on RMSof relative distance
由图3可以看出,侧向阵风作用时相对距离均方根值很小,因为侧风的干扰作用主要表现在对侧滑角的影响,使弹体产生一个附加的侧滑角Δβ≈W3sin(ψ'-ψ)/V,而侧向阵风风速 W3相比弹体速度V要大很多,即风对弹体的侧滑运动影响不大,产生的脱靶量很小。
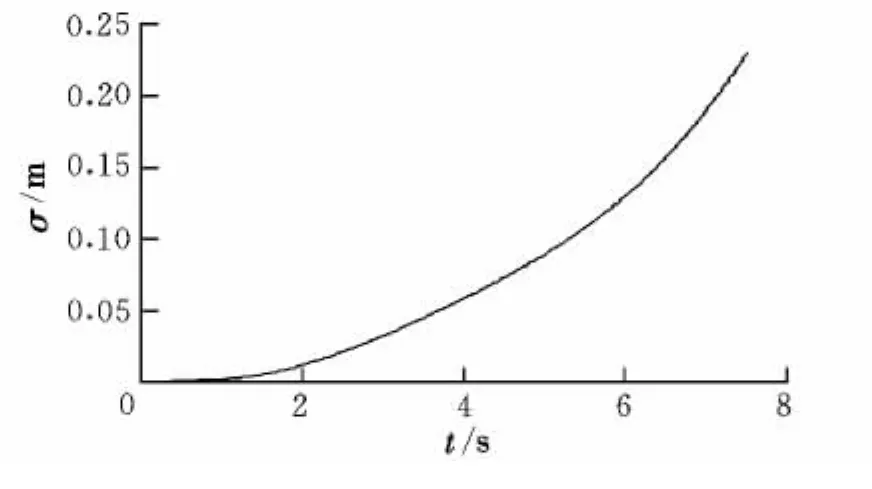
图4 导引头噪声对相对距离均方根的影响Fig.4 Effect of seeker noise on RMSof relative distance
由图4可知,导引头噪声对相对距离均方根的影响随导引时间的增加不断增大。相比侧向阵风的作用,导引头噪声的影响更为显著。
在目标机动、侧向阵风及导引头噪声这三个因素中,影响相对距离均方根最主要的因素是目标机动,其次是导引头噪声,而侧向阵风的作用十分有限。
将目标机动、侧向阵风及导引头噪声全部加入到系统中,运用SLAM进行计算。为了便于比较各种方法的优劣,还分别采用CADET和Monte-Carlo进行了仿真计算,其中Monte-Carlo分别进行了n=200,300,400,500 次试算,在图 5 中只给出了 n=400,500次的计算结果。
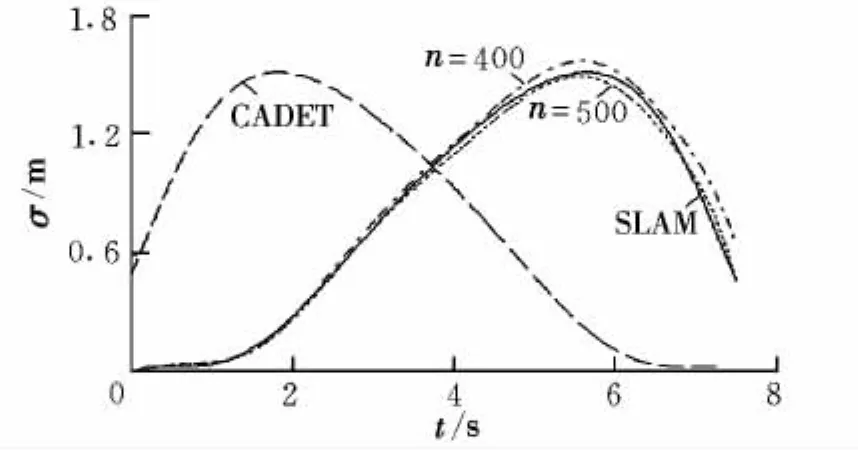
图5 综合干扰因素对相对距离均方根的影响Fig.5 Effect of comprehensive interference factors on RMSof relative distance
从图5可以看出,SLAM的结果与Monte-Carlo进行了500次计算的结果基本接近,且反映的均方根变化规律一致,两者具有同等的计算精度,只是因为伴随时间(tadd=tf-t)使均方根曲线反向;SLAM除了得到相对距离均方根,还能够得到各个干扰项对均方根散布的影响,因此SLAM比CADET更具有优越性,是评价导弹制导系统精度更为有效的工具。
5 结束语
以某型导弹制导系统为例,综合考虑目标机动、随机风干扰以及导引头噪声的作用,对导弹制导精度进行了统计分析。研究了各种随机干扰对总均方根值的影响,并与CADET和Monte-Carlo的仿真计算结果进行了比较,得到了更为全面、有效的分析结果,为导弹制导系统的性能分析和优化设计提供了有力参考。
[1] 林晓辉,崔乃刚,刘育华.协方差分析描述函数法在导弹惯性末制导精度计算中的应用[J].航空兵器,1997,(3):10-12.
[2] Gelb A,Warren R S.Direct statistical analysis of nonlinear systems:CADET[J].AIAA Journal,1973,1(5):689-694.
[3] 周卫文,梁晓庚,贾晓洪.自寻的导弹末制导系统仿真分析方法研究[J].计算机仿真,2012,29(8):45-46.
[4] Zarchan P.Complete statistical analysis of nonlinear missile guidance system_SLAM[J].Journal of Guidance,Control,and Dynamics,1979,2(1):71-78.
[5] 韩松臣.导弹武器系统效能分析的随机理论方法[M].北京:国防工业出版社,2001:42-43.
[6] Tarlor JH.战术导弹制导系统直接统计分析手册[Z].赵善友,译.上海:第8250研究设计所,1978.
[7] 郭庆,杨明,王子才.拦截器末制导段误差模型的建立与仿真[J].计算机仿真,2007,24(3):58-61.
[8] 张望根.寻的防空导弹总体设计[M].北京:宇航出版社,1991.
[9] 刘金,关世义,常伯浚.CADET方法在反舰导弹脱靶量研究中的应用[R].北京:机电工程研究所,1991.
