基于粗糙集的相邻交叉口信号控制方法研究

李璐兵，陈荣升

（北京交通大学交通运输学院，北京100044）

0 引言

城市道路交通系统是一个时变的，具有随机性、不确定性的复杂系统。随着城市交通量的快速增长、城市道路网建设的不断完善，尤其是路网密度的增强，交叉口之间的相关性日益明显，城市对交通信号控制提出了更高的要求。近年来在协调控制模型建立与协调控制策略选取方面，相关学者做出了大量尝试，也取得了相应的成果。模糊交通控制已成为交通信号控制的主流方向之一，许多研究成果也得以在实践中应用，但模糊控制也存在许多诸如隶属度函数的选取、模糊控制规则的形成大量掺杂人为主观因素等问题，这些因素都对整个控制的效果产生影响。

目前，将粗糙集理论应用于交通工程领域的研究已经有了许多研究成果。郑梦泽将粗糙集理论与交通控制结合起来，对交通控制过程中的属性进行了分析，并将粗糙集理论的知识获取和决策分析算法应用到单点交叉口信号控制中[1]。杨柳等人提出了基于粗糙集理论的公交优先的控制算法[2]，对于相邻交叉口的研究也取得了较多成果。郑长江、吴金花对行人过街信号与交叉口信号联动控制的研究介绍了城市主干道模糊控制方法[3]。卢凯、徐建闽等通过分析相邻交叉口间距、路段交通量以及交叉口信号配时参数对相邻交叉口关联性的影响，提出了关联度的概念，对相邻交叉口之间关联性进行了定量化描述[4]。

针对城市交通流特性和交通拥堵形成原因，本文选取交大东路上两个关联度较高的交叉口作为研究对象，对相邻交叉口信号控制决策过程中某些不确定性问题和交通情况的影响因素进行分析，阐明了粗糙集方法在实际信号控制中的应用，提出粗糙控制系统的粗糙集模型，对属性数据进行挖掘，最终提出基于粗糙集理论的相邻交叉口信号控制决策方案。

1 粗糙集理论

粗糙集理论在1982 年由波兰科学家Z.Pawlak创立，它最显著的优势是它不需要提供问题所需处理的数据集合之外的任何先验知识，粗糙集理论研究的出发点就是直接对数据进行分析和推理，从中发现隐含的知识，揭示潜在的规律，是一种天然的数据挖掘和知识发现方法。

知识的约简是粗糙集的核心内容，在知识约简中有两个重要概念就是核与约简。在条件属性到决策属性的映射中，一组或者多组属性对应一个决策，形成一对一或多对一的关系。若去掉某个条件属性，在条件属性和决策属性间仍存在一对一和多对一的关系，不存在一对多的关系，即对原来的对应关系没有影响，则该属性为非必要属性，可以去掉这个冗余的非必要属性。如果Q是独立的，则称Q为P的一个约简。记为一族等价关系P可能有多个约简，全部约简的交集定义为P的核（Core），记为core(p)=⋂red(p)。

2 问题分析

本文以北京市交大东路上相邻两个交叉口为研究对象，优化两个交叉口信号灯的联动控制方案，调查区域示意图如图1所示。交叉口一为交大东路与交大家属区东门的交叉区域，南北方向有直行机动车，东西方向有行人通过，该信号灯周期为90s，其中红灯时长28s，绿灯时长62s。交叉口二为交大东路与交通大学路交叉区域，交大东路上南北向左转车辆较少，在建模时忽略不计。交叉口二信号周期为86s，其中红灯41s，绿灯45s。交叉口一与交叉口二距离为350m。通过在早高峰对20 组车辆在该路段上的通行时间的统计，得出车辆通过该路段的平均时间为45s，平均车速为28km/h。在早晚出行高峰经常会出现东西方向上绿灯相位时间过长，南北向上游排队车队过长溢出至下游交叉口，导致交叉口通行效率降低。在调整后的方案中交叉口一与交叉口二采用相同信号周期，系统速度为28km/h，即相位差45s。由设置在各交叉口进口道的检测器检测交通流状况，通过粗糙控制模型对信号灯实时感应控制。

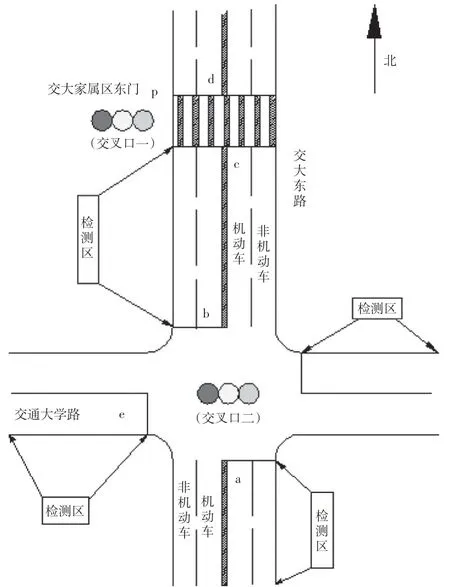
图1 调查区域示意图

采集数据包括：a、b、c、d 四车道绿灯转换红灯时刻检测区域内车辆总数以及移动车辆总数；e 车道红灯时检测区域内排队车辆数；p 区域内红灯相位等待过街的行人数量（包括闯红灯的行人）。

3 粗糙控制模型

粗糙控制[5]的基本思路是将车辆检测器实时获取的交通流数据经过预处理作为对交通信号控制的条件属性，然后建立决策表，利用RS 理论的约简算法删除多余的属性得到最简规则保存到知识库中作为对交通信号粗糙控制的主要依据。流程设计图如图2所示。

图2 控制系统流程

3.1 参数设定

3.1.1 绿灯相位时车辆阻塞参数b[6]

为了能准确反映车道上的拥挤程度，引入阻塞参数b，定义为：

本文中在测量绿灯时的阻塞参数时由于车辆多处于跟驰状态，因此取车辆的平均长度为10m。检测区内（120m）最多可以容纳车辆为12 辆，则为平均速率，等于车道上能够移动的车辆数与车道上车辆总数的比值。

3.1.2 红灯相位车辆拥挤度α[7]

定义车辆拥挤度为：

α为0～1之间的数，是由信号交叉口前后两个检测器之间的车辆数除以两检测器之间能检测到的理论最大车辆数，α的值越大表示越拥挤。

3.1.3 行人过街排队拥挤度δ

定义行人拥挤度为：

式中：A为红灯相位等待过街的行人数；T为交叉口能够容纳的最大行人数量。

3.1.4 决策属性

决策属性为绿灯延时E=｛0，6，9，12｝。南北方向固定绿时50s，最大绿灯延时36s。

3.2 控制程序

在该算法中，交叉口处车辆进入检测区时，将根据检测到的车辆信息计算绿灯相位的阻塞参数与红灯相位的拥挤度，并根据设计好的粗糙控制系统自动调整绿灯相位的延长时间，使交通信号根据车流情况更合理地分配相位时长，提高交大东路上车流的实际通行能力，减少交叉口停车延误和停车次数。

步骤1：结束上一红灯相位，执行固定时长绿灯相位Gfix，最大绿灯时长为Gmax；

步骤2：通过粗糙集模型计算绿灯延时GD。若GD=0，则结束当前绿灯相位切换到红灯相位；若GD≠0，则令G=Gfix+GD；

步骤3：当G＞Gmax时，结束当前绿灯相位切换到红灯相位；

步骤4：当G≤Gmax时，执行GD，令Gfix=Gfix+GD，返回步骤2。

流程图如图3所示。

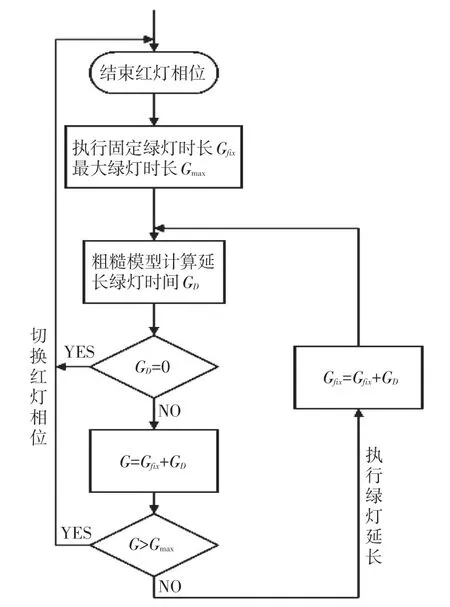
图3 算法流程图

4 算例分析

4.1 数据离散化

将交大东路与交通大学路相交的交叉口北南方向的绿灯车辆阻塞参数定义为Ua，Ub；将交大家属区出口人行横道两侧的车辆阻塞参数定义为Uc，Ud；交通大学路交叉口西口的红灯相位拥挤度定义为Ue，家属区东门的行人拥挤度定义为Up。令E=[0，1]，则Ua，Ub，Uc，Ud，Ue、∈E。由于采用RS 理论对数据分析时要求数据是离散的，所以需要对连续属性的数据离散化处理。

离散后的结果为：将Ua，Ub划分为4 个区间A（0.70，1.00]，B（0.50，0.70]，C（0.30，0.50]，D[0，0.30]；将Ub，Uc划分为4 个区间，分别为A（0.80，1]，B（0.60，0.80]，C（0.35，0.60]，D[0，0.35]；将Ue划分为4 个区间，分别为A[0.50，1.00]，B[0.30，0.50），C[0.15，0.30），D[0，0.15）。将Up划分为4 个区间，分别为A[0.60，1.00]，B[0.40，0.60），C[0.15，0.40），D[0，0.15）。

论域U表示当前绿灯即将结束时整个路口的状态，U=⋃{ }Ua,Ub,Uc,Ud,Ue,Up。xi∈U(i=1,2,3,…,50)表示采集的每一组数据。则有|U|=50，具体状态组合如表1所示。

表1 数据分组

4.2 知识划分

通常情况下，在求解问题的过程中，处理的是论域U上的一簇划分，这引出了知识库的概念。论域上的等价关系代表着划分和知识，知识库就表示了论域上的由等价关系导出的各种知识，即划分或分类模式[8]。定义粗糙控制模型知识库为：

R1：当绿灯累计时间不超过最大绿灯时间，可延长当前绿灯相位的绿灯时间；

R2：当车辆绿灯阻塞参数Ua或Ud为D时，延长当前绿灯时间；

R3：当车辆绿灯阻塞参数Ub或Uc为D时，延长当前绿灯时间；

R4：当绿灯累计时间超过最大绿灯时间时，结束南北向绿灯相位；

R5：当Ua，Ub，Uc，Ud均不为D时，若Ue为A时，结束南北向绿灯，东西向变为绿灯；

R6：当Ua，Ub，Uc，Ud均不为D时，若Up为A时，结束南北向绿灯，东西向变为绿灯。

根据给定的知识库K=(U,S)和论域U上的等价关系R∈IND(K)将论域U划分为：正域|R_(X)|负域|negR(X)|=7，上近似边界域论 域相等，这说明决策表是完全确定的决策表，决策表中不包含不一致的信息。

4.3 决策表

根据知识R划分结果，确定南北向绿灯相位结束时绿灯延长时间E。根据经验设定累计最大绿灯延长时间Gmax=18s。延时分为完全延时和不完全延时，其中正域为完全延时，完全延时时长C=12s，负域同样为完全延时，延长时间为C=0s，边界域为不完全延时，这里引入绿灯延时率γ以确定边界域的绿灯延长时间，定义如下[2]：

其中正域绿灯延长率γ =1，负域绿灯延长率γ=0，边界域绿灯延时率由以下函数确定：

则论域U及其决策属性如表2所示。

表2 决策表

4.4 属性约简

4.4.1 非必要属性剔除条件属性集合F={Ua,Ub,Uc,Ud,Ue,Up}，决策属性集说明该决策表为完全确定的决策表，表示决策表中不包含不一致的信息，即同样的条件属性组合对应不同的决策属性。依赖度可以这样计算，如决策属性E依赖于条件属性F的依赖度为：

对于属性集合，若去掉Ua，再对Ub、Uc、Ud、Ue、UP进行划分，可以得到条件属性集去掉属性Ua之后的等价划分U/F-{Ua}。计算得依赖度为说明对于决策属性E而言，Ua是非必要条件属性的。同理计算Ub,Uc,Ud,Ue,UP的依赖度，确定了Ub,Uc,Ue,Up为必要条件属性。将非必要属性剔除之后可得到20条规则。

4.4.2 规则简化

为使算法简化，对于有多种约简方式的规则只选取其中一个作为构成原算法的最简算法。最简算法的形式为if“条件1”and“条件2”…and“条件N”，then“结论或动作”。简化后的规则如下：

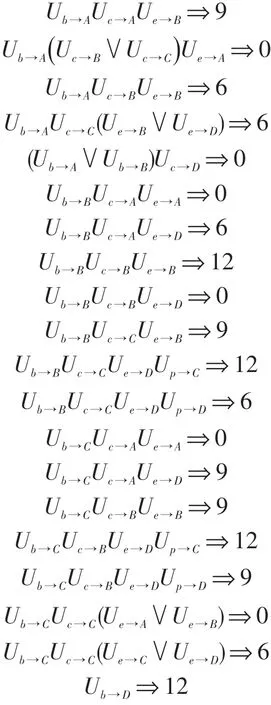
5 结语

本文在分析交通信号控制原理的基础上，结合交大东路实际情况，提出了一种基于粗糙集理论实现对相邻两个交叉口的信号联动控制算法，结果表明RS理论是一种处理交通信号动态控制的理想工具，同时也为多交叉口群的交通管理与控制提出了一种新的思路，是RS在交通领域应用的一次有益尝试。

[1] 郑梦泽.基于粗糙集的交通信号控制决策研究[J].通信技术，2010，43（4）：225-227.

[2] 杨柳，彭小波，王当仁.基于粗糙集理论的公交信号优先算法研究[J].交通标准化，2013（21）：127-129.

[3] 郑长江，吴金花.实时模糊控制的行人过街信号与交叉口信号联动控制[J]. 贵州大学学报：自然科学版，2011，28（6）：98-103.

[4] 卢凯，徐建闽，郑淑鉴.相邻交叉口关联度分析及其应用[J]. 华南理工大学学报：自然科学版，2009，37（11）：37-42.

[5] Toshinori Munakata, Zdzislaw Pawlak. Rough Control Application of Rough Set Theory to Control[C]//Proceeding of Fourth European Congress on Intelligent Techniques and Soft Computing. Aachen: Fourth European Congress on Intelligent Techniques and Soft Computing,1996:209-218.

[6] 王艳娜，周子力，王新伟.基于模糊控制的多相位交叉口交通信号控制[J].计算机工程，2006，32（2）：229-231.

[7] 李元元，巨永锋.城市信号交叉口公交优先及模糊控制策略[J].现代电子技术，2006，29（15）：155-157.

[8] 苗夺谦，李道国.粗糙集理论、算法与应用[M].北京：清华大学出版社，2008.