改进灰色预测模型在城市用水量预测中的应用

■罗 松，孙传斌 ■九江市城市规划市政设计院，江西 九江 332000

城市用水量预测对于城市规划、供水系统的管理及指导城市供水设施的建设有着重要的意义。随着我国城市与工业生产的规模不断扩大，水作为城市生存和发展的制约性因素，在我国大部分城市成为稀缺资源，全国2/3的城市面临缺水。合理地预测城市用水量，对城市具有显著的社会意义和经济意义。目前，常用的城市用水量预测方法有年增长法、GM(1，1)灰色模型法、时间序列法、回归分析预测法等。

GM(1，1)模型具有要求历史用水量数据少、不考虑分布规律、不考虑变化趋势、运算方便、易于检验等优点，因此得到了广泛应用，并取得了令人满意的效果。但是还存在这一定的局限性:一是当数据离散程度越大，即数据灰度越大，则预测精度越差;二是不太适合给水系统的长期后推若干年的预测［1］。所以，需对预测模型进行一定的改进，使得预测精度(0)(k+1)=(1)(k+1)-(1)(k)高。

Verhulst模型是1837年德国生物学家Verhulst在研究生物繁殖规律时提出的。其基本思想是生物个体数量是呈指数增长的，受周围环境的限制，增长速度逐渐放慢，最终稳定在一个固定值。Verhulst模型主要用来描述具有饱和状态的过程，即“S”型过程，常用于人口预测、生物生长、繁殖预测及产品经济寿命预测等［2］。

1 模型介绍

1．1 GM(1，1)模型

设为x(0)为n个元素的原始数列:

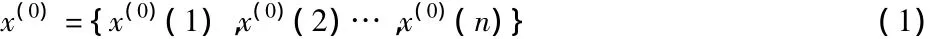
其中，x(0)(k)≥0，k=1，2，…，n;

x(1)为x(0)的一阶累加(1-AGO)序列:

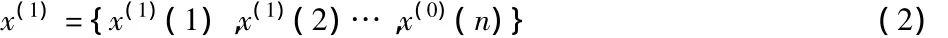
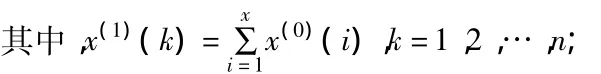
z(1)为x(1)的紧邻均值生成序列:

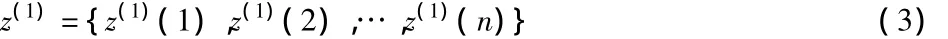
其中，z(1)(k)=0．5x(1)(k)+0．5x(1)(k-1);k=2，3，…，n．

建立灰色GM(1，1)模型的一级白化微分方程为

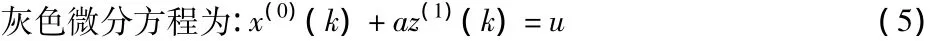
其中，a—为发展系数;u—为灰色作用量。

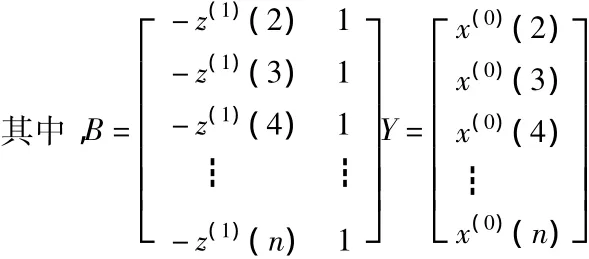
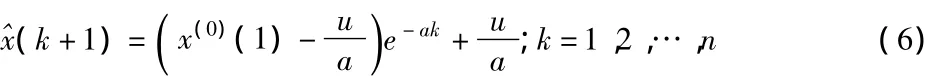
对此式做一阶累减(IAGO)还原计算，得原始序列的GM(1，1)预测模型为:

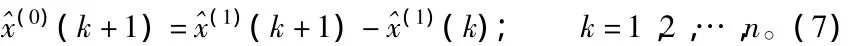
1．2 新陈代谢GM(1，1)模型

随着观测时间的推移，不断有新的观测信息加入原始序列中，使得数据信息量不断丰富。由于数据值不断增长，早起数据所占份额逐渐减少而显得较为次要，于是提出有了新陈代谢模型，也就是在增加一个新信息的同时，把最早的一个老信息删掉，从而维持数据总量保持不变［3］。

新陈代谢处理后x(0)得:

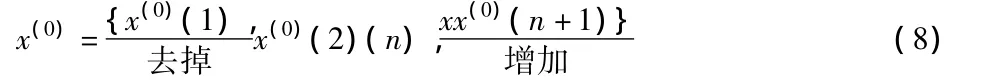
接下来重复GM(1，1)模型(2)～(7)进行建模计算

1．3 灰色Verhulst模型

根据原始数据序列x(0)分别得到一次累加新数据序列x(1)以及紧邻均值生成序列z(1)，建立灰色Verhulst模型的白化微分方程为:

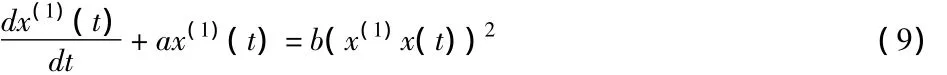
a、b 含义同 GM(1，1)模型，a——发展系数，b——灰作用量。

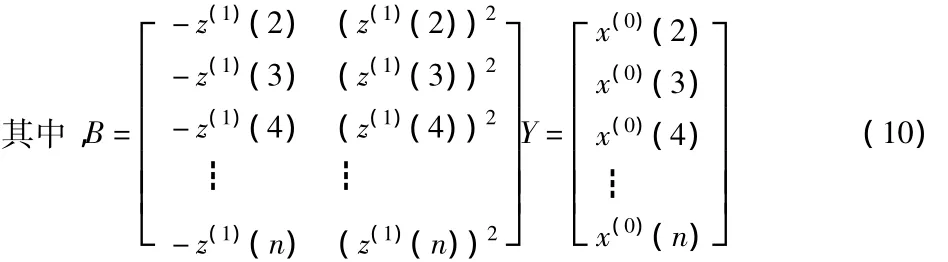
灰色Verhulst模型的时间响应式:

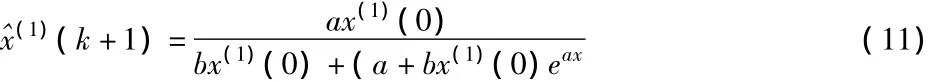
其中，k=1，2，…，n-1

的Verhulst预测模型还原值为:

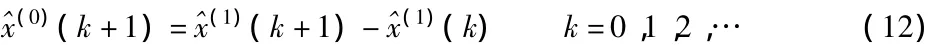
当 k→∞时，若a＞0，则x(1)(k)→0;若a＜0，则x(1)(k)→，即有充分大的k使x(1)(k+1)和x(1)(k)充分接近，此时x(0)(k+1)=x(1)(k+1)x(1)(k)≈0，系统趋近死亡，在处理“S”型或部分“S”型过程时预测精度更高。

2 模型精度检验实例分析

一般认为，预测精度≥85%，则认为预测是成功的［3］。目前预测值精度分级的一般原则如表1所示，表中MAPE为平均绝对百分比误差，其计算公式如下:

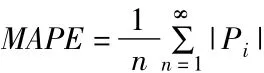
式中:n—样本数据个数;Pi—相对百分比误差(%)。

表1 预测精度划分表

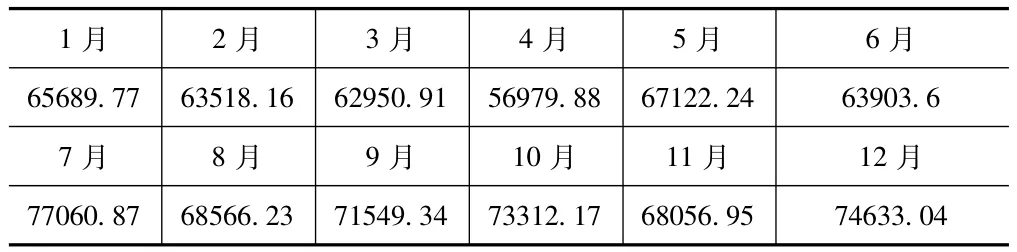
表2 陕西省某城镇水厂2010年的供水量(单位:m3)

对该城镇1月～9月用水量进行建模，预测10月～12月用水量。

从表3可以得出，GM(1，1)模型、新陈代谢GM(1，1)模型以及灰色Verhulst模型的MAPE分别是6.16%、5.32%、6.07%，都属于高精度预测。预测效果:新陈代谢GM(1，1)模型＞灰色Verhulst模型＞GM(1，1)模型。

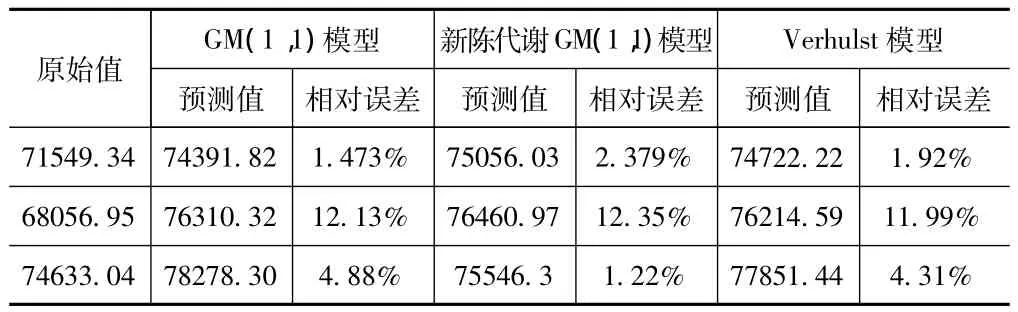
表3 用水量预测值与实际值的比较结果

3 结论

本文采用灰色系统理论对城市用水量进行预测，针对GM(1，1)模型存在的问题，提出了新陈代谢GM(1，1)模型。结果表明，新陈代谢模型(动态等维新息模型)比基本的GM(1，1)模型和Verhulst模型预测精度更高，拟合效果更好，适用于城市的用水量预测。

［1］尹学康，韩德鸿.城市需水量预测［M］.中国建筑工业出版社，2006(2):111.

［2］郭广猛.用 GM(1，1)模型和Verhulst模型进行建筑物沉降预测［J］.岩土工程界，2000，3(10):33-37.

［3］赵鸿宾.给水管网系统理论与分析［M］.中国建筑工业出版社，2003.