留预备队的思想与预备队最佳预留方案研究
2014-12-25严建钢杨士锋
严建钢 杨士锋
(海军航空工程学院,山东 烟台264001)
1 引言
战斗是具有主观能动性的双方之间进行的对抗。为了取得优势并利用优势取得胜利,战斗双方总是力图采取一些对方预料之外的策略。正因为如此,在战斗中,并不是所有的情况都可以预料得到:有些情况预料到了但没有发生,有些情况没有预料到却发生了。预备队就是为了应付这些意外情况而专门组建的预备力量,对于预备队的运用是作战决策迫切需要研究与解决的问题。
目前,关于预备队预留问题的把握,主要是根据我军丰富的作战经验,按照总兵力的一定比例进行掌握与控制[1]。这种方法处理问题简单,宏观性强,对指导我军作战确实起到了很大的作用。但是,在敌方兵力变化或在己方兵力紧张的情况下,这种按一定比例预留的原则是否还适用呢?本文针对这个问题,根据兰彻斯特方程、作战理论以及运筹学原理,提出了战争(战斗)预备队力量使用最佳方案的概念,并建立了预备队最佳预留模型,解决了在有限资源的情况下合理使用战争(战斗)各种力量的问题,使有限的资源发挥最大的效益。
2 留预备队思想的数理剖析
本文以一个实际的数值例子,用多战场的兰彻斯特方程来说明留预备队的策略是一种好的策略[2,3]。
2.1 问题描述
假定甲、乙双方发生一场战斗,乙方拟向甲方进攻,可能的战场有三个:主要进攻方向1,也即主要防御方向1;次要进攻方向2,也即次要防御方向2;甲方的大本营3。在大本营处交战有利于乙方进攻而不利于甲方坚守,所以乙方只要在主要进攻方向1 或次要进攻方向2 上有一处突破,就可长驱直入进攻甲方的大本营3,而甲方则要分兵把守主要防御方向1 与次要防御方向2,使其不能突破防线,一旦发现有一处吃紧,就可将留在大本营的预备队派往该处防守。现在进一步假定双方都为单兵种作战,乙方集中全部初始兵力于主要进攻方向1 或者次要进攻方向2,在另一个方向的佯攻或牵制等部队不明显地反映在模型中。事先甲方并不知道乙方的企图究竟是在哪一个方向进攻,甲方初始兵力x0中分x10于主要防御方向1,x20于次要防御方向2,留x30= x0-x10-x20于大本营。一旦发现乙方向主要进攻方向1 攻击时,甲方就将预备队x30全部派往方向1,在T1时间后即可到位作战;一旦发现乙方向次要进攻方向2 攻击时,甲方就将预备队x30全部派往方向2,在T2时间内即可到位作战。大本营的直接保卫、警戒部队等另行留出,也不明显地反映在模型中。已经部署到次要防御方向2 的部队x20由于种种原因,不能增援方向1。同样已经部署到主要防御方向1 上的部队也不能增援方向2。
如果取x30=0,就是不留预备队;如果取x10=x20=0,就是固守大本营,不在主要防御方向1 与次要防御方向2 部署防御力量。这两种极端情况可以作为一般情况的对比,现在的问题是如何分配x10、x20与x30,使甲方在抗击乙方进攻时效果更好。
2.2 兰彻斯特建模分析
进一步假定在三个不同战场交战的兰彻斯特方程如下:

初始兵力x0=10000,y0=12000,T1= T2=
ln1.25。
例子中所有参数的选择,特别是战场1 与战场2 参数的一致性,都是为了说明问题与讨论方便起见精心选取的,但其结论仍不失普遍性。现讨论以下三种方案。
2.2.1 方案1
甲方不留预备队,即取x10= x20=5000,x30=0。
假定乙方集中全力从主要方向1 进攻,则在战场1 的兰彻斯特方程的解为:

在这种部署下,甲方不能有效抵抗乙方的进攻,可以证明,该方案下甲方最多能有效抵抗乙方初始兵力y0=10000 的进攻。
2.2.2 方案2
甲方全部留在大本营,即取x10= x20=0,x30=10000。
这时乙方可轻易通过战场1、2 中任意一个方向进攻,直接到甲方大本营决战,此时在战场3 的兰彻斯特方程的解为:

甲方对兵力适当配置,取x10= x20=3000,x30=4000。
假定乙方将全部兵力用于战场1,则开始时战场1 的兰彻斯特方程的解为:

战斗开始后,甲方知道战场1 吃紧就将全部预备队x30派往战场1,经时间T1=ln1.25 后到达战场1。在预备队到达前的瞬间:

当预备队到达后,甲方实力变为:
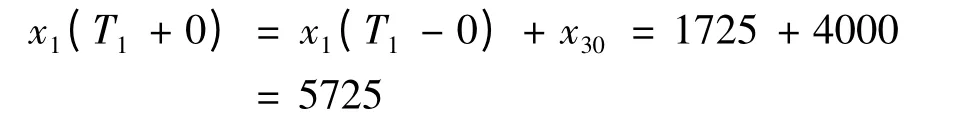
乙方实力不变。从T1时刻起算,战场1 处的兰彻斯特方程的解为:

显然这时乙方不能突破主攻方向,甲方有效地抵抗了乙方的进攻。这种情况下,若乙方在主要进攻方向1 与次要进攻方向2 上分兵进攻显然效果更差。
对以上三种作战部署方案的分析说明,无论是倾巢分兵把守还是全部留守,都不能抵御敌方的进攻,只有适当留预备队才是克敌制胜之道。这一结论与军事常识中留预备队的战术是一致的[4-6]。
3 预备队投入时的作战模型
为了说明预备队的使用对作战胜负的关键作用,尽量减少双方战术优劣等其他因素对作战的影响,可将双方兵力都看作一个整体,使用单兵种作战的兰彻斯特方程。假设甲、乙双方交战,甲方投入兵力的初始值为x0,且一次性投入战斗;乙方共有兵力为y0,且分期分批投入,这就是一个预留预备队的问题。针对这一特点,下面讨论一方留有预备队的作战模型。
设乙方留有一部分预备队兵力,在一定时间T内,按一定补充速度K投入战斗,其他条件不变,那么双方的作战模型为:

这时乙方兵力的初始条件y00为:总的投入兵力y0与在此模型下作战时间T内补充兵力K·T之差。即:
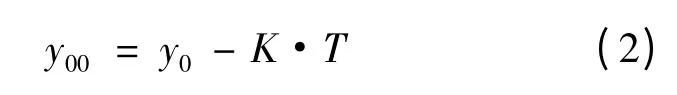
定理1:设甲、乙双方作战,甲方全力展开攻击乙方,乙方留取一定的兵力作为预备队,逐次展开增援,双方的初始实力为x(0)= x0,y(0)= y00=y0-K·T,则留预备队的作战模型(1)有唯一解为:

[7]中定理3.1,可得到式(3)。
设:

则由式(1)得:

变形为:
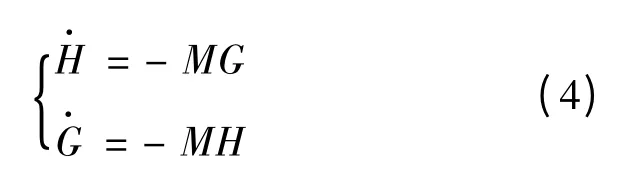
式(4)在形式上与参考文献[7]中定理3.1 完全相同,从参考文献[7]的定理3.2 知,甲方要取得胜利,必须是使

成立,而留预备队作战模型,甲方获胜条件是:

即:
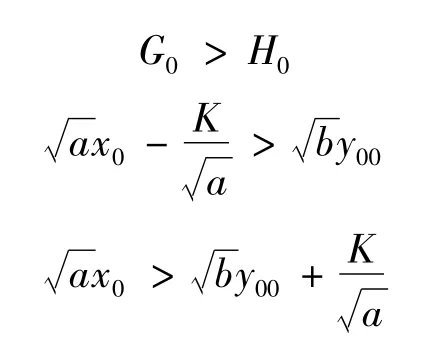
将式(2)代入得:
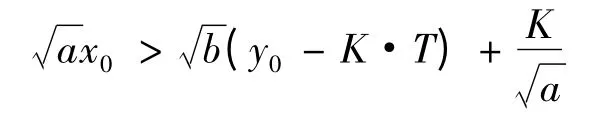
将参考文献[8]中3.6 代入得:

设:

再设:

式(9)说明在乙方留有预备队逐次展开增援的情况下,甲方获胜的条件发生了变化,这是一个重要的发现,对研究是否留预备队以及怎样留提供了依据。
4 预备队预留的最佳模型
式(9)与式(5)相比,差别在于不等式右边反映乙方实力的数值发生了变化,说明了留不留预备队确实影响双方作战实力的表现程度,从而影响作战进程与结果,这是一个重要的作战决策问题。
对式(7)进一步分析可以得出许多有价值的信息。式(9)与式(5)相比的变化项是:
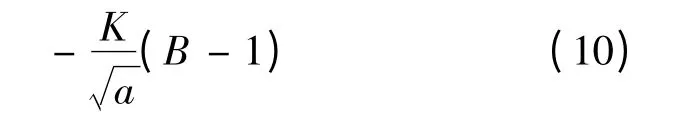
式(10)中,K与a分别是乙方预备队的增援速度、甲方攻击乙方的威力系数,它们都是大于0 的参数,那么式(10)的符号就取决于B的取值情况。
当B <1 时,式(10)始终是一个大于0 的数,说明乙方总的作战实力是增加了,按照这种方式预留预备队是一种好的策略。
当B >1 时,式(10)始终是一个小于0 的数,说明乙方总的作战实力是减小了,按照这种方式预留预备队是一种坏的策略,不但没有增加实力,反而减小己方的作战能力,把可能到手的胜利拱手让给了对方,得不偿失。
当B =1 时,式(10)始终为0,双方的实力都没有发生变化,这种预留预备队的方案是好是坏,不能笼统地下结论,必须根据具体情况加以分析。
从以上三种情况分析可以看出,B值全面反映了留预备队可能出现的各种情况,下面根据式(8),分析各种预留预备队方案的利与弊。
从式(8)中可以看出B值的取值情况又取决于R值,而R值取决于式(7),即:

定义1:甲、乙双方按照单兵种对单兵种交战,双方的杀伤系数为a、b,双方初始投入兵力为x0、y0,称R为交战双方实力差强度函数。当>0 时,称R为正强度函数;当时,称R为负强度函数;当时,称R为无差别度函数。
实力差强度函数R的大小直接反映B的取值情况,根据式(8)看出B值随R函数呈自然对数规律变化,可以通过调整R值的大小,来调整B值的大小。
定义2:甲、乙双方交战,一方全力以赴展开兵力交战,一方按照一定的预留兵力持续展开进行交战,由实力差强度函数R确定的B,我们称为预备队预留值比较函数,由此确定的模型(9)称为预备队预留判断模型。
通过对预备队预留判断模型(9)的分析,可以得到在一定的作战态势下是否留预备队,留多少。如不具备条件,是否调整兵力投入,预留一定数量的预备队,达到最佳作战效果。下面用定理的形式给出。
定理2:设甲、乙双方作战,甲方全力展开攻击乙方,乙方留取一定的兵力作为预备队,逐次展开增援,双方的初始实力为x(0)= x0,y(0)= y00=y0-K·T,则当时,可以预留一部分兵力为预备队,其预留兵力yl为:

式(12)中K可以根据作战的实际需要,由指挥员确定。当B =ln ■R >1 时,不宜留预备队,如特别需要留有一部分预备队,则通过调整兵力的投入y0,使yl达到:

当B =ln ■R =1 时,可以根据战场的实际情况确定留不留预备队和预留预备队的具体方案。
定理2 说明了一个非常重要的战术思想,在兵力一定的情况下留不留预备队主要取决于交战双方实力差强度函数R。R值较大时,说明战场上力量弱的一方承受压力较大,如果这时再分配一定比例的兵力留作预备队,势必加大己方战场上的压力,预备队预留值比较函数B增加,总体上削弱己方总的作战能力,影响全局作战的效果。只有在强度函数R值较小时,说明战场上力量弱的一方承受压力较小,如果这时分配一定比例的兵力留作预备队持续展开攻击对方,预备队预留值比较函数B减少,总体上增加己方总的作战能力,可以使作战资源的能力充分发挥出来,取得最佳的作战效果。
5 结论
利用比较函数B确定预备队预留的策略,不但考虑了己方兵力的情况,而且还考虑了敌方的兵力情况,将敌我双方的兵力综合起来进行定量考虑,使预备队的预留兵力建立在科学分析计算的基础上,做到了定性与定量、经验与理论相结合。本文中比较函数B的推导是建立在兰彻斯特“平方率”方程基础上,如果能够建立信息化条件下的兰彻斯特方程,比较函数B也适用于信息化条件下预备队预留方案的制定。
参考文献
1 江宁.高级战术学导论[M].北京:解放军出版社,2011.
2 薛兴林.战役理论学习指南[M].北京:国防大学出版社,2002.
3 国防大学.战役学[M].北京:国防大学出版社,2000.
4 刘金胜.战役[M].北京:中国大百科全书出版社,2007.
5 宋晓军.中外著名战役[M].北京:星球地图出版社,2012.
6 Eastern RAND Report.美军专家探讨战役预备队的过去,现在与未来[J].国际防务译文,2011(14):6 -13.
7 沙基昌.数理战术学[M].北京:科学出版社,2003.
8 严建钢.航空兵数理战术分析[M].北京:解放军出版社,2006.
