Decision Bayes Criteria for Optimal Classifier Based on Probabilistic Measures
2014-12-24WissalDriraandFaouziGhorbel
Wissal Drira and Faouzi Ghorbel
1.Introduction
In the last decade, the major technological advances have led to explosive growth in the size of data, where the number of variables is often in the hundreds or thousands and sometimes much larger than the number of observations.Classification of such a high-dimensional data is a difficult problem that appears in many sciences.The difficulty of this problem comes from the large number of variables that present challenges to conventional classification methods and makes many conventional techniques impractical.A natural solution is to add a dimension reduction step before proceeding to the classification phase.Many discriminate analysis methods have been proposed in the literature such as linear discriminate analysis (LDA), approximation of the chernoff criterion (ACC), and information discriminate analysis(IDA).In our previous work, we introduced a nonparametric probabilistic discriminate analysis method based on a new estimate of the Patrick-Fischer distance for binary classification[1]and an estimator to the L2-probabilistic dependence measure (L2-PDM) as an extension to the multi-class case[2].Since this stochastic approach is based on probabilistic distances, theoretically this method approaches indeed the nonparametric Bayes classifier.Unfortunately, in practice, the optimization of this algorithm cannot be solved analytically.
In this sense, we propose an optimization algorithm of the L2-PDM in order to approximate the Bayes classifier based on the adjusted kernel method estimation with the smoothing parameter.This optimization is illustrated in Section 3.With the aim to illustrate this fact, a performance evaluation by using the means of the misclassification error is performed and illustrated by simulation data, then we present experimental results for the UCI machine learning repository of data bases[3].We also conduct a comparative study between different pairs (discriminate analysis,classifier) to interpret and improve the classification results.
2.Probabilistic Approach for Reduction of Dimensions
In the pattern recognition field, reducing the dimension of a feature vector for a statistical pattern classifier is desirable for some reasons: it results in lower computational and memory demands of the system, and the decrease of the number of model parameters to be estimated to achieve more accurate estimates for a limited training database.In this sense and in his groundbreaking work, Fisher defined an easy and fast algorithm to reveal the sub-dimensional space that minimizes the Bayes error in a binary classification problem[4].This solution, known as LDA, is not guaranteed to find the optimal subspace dimension in some complex cases.Various techniques have been introduced to improve it, such as the one based on the Chernoff distance.This was introduced in [5]by Loog and Duin named ACC that maximizes the Chernoff distance in the original space to minimize the error rate in the transformed space.Another approach called IDA is based on the optimization of an objective function by using mutual information[6].These methods are defined either using statistical moments of the order less than or equal to two like in the case of LDA and ACC, or based on the hypothesis about the type of the law of distribution like the condition of heteroscedasticity (LDA, ACC, and IDA).
However, in more general cases, these methods fail todescribe completely the statistical dispersion of data. To address these limitations, the distance between the probability density functions weighted by apriority probabilities was introduced by Patrick and Fischer[7]. They proposed a kernel estimator of their distance in the scalar discriminate analysis case (d=1). The extension to the multivariate case was introduced in [2] and [8] with an estimate of the L2-PDM using orthogonal functions. As a generalization, the dimension reduction criterion corresponding to the specified discriminate analysis can be summarized as the search for a vector W*maximizing such criterion in the reduced space d. This criteria can be interpreted also as the objective function of the LDA, ACC,IDA or L2-PDM methods, represented respectively as the Fisher criterion, the Chernoff criterion, the μ-measure,and the estimator of the L2-PDM ().
Unlike LDA and ACC, the optimization in the IDA and L2-PDM methods does not admit an analytical solution.Numerical optimization methods are then implemented for the L2-PDM to approaching the Bayes classifier in a nonparametric case and for large dimensions. This system will be described in the next section.
3. Toward Nonparametric Bayes Classifier
We need the following approximations: First, we estimate the linear transformation which maximizes the estimated L2-PDM according to the distribution of the training samples and the initialization of the linear transformation W0. We recall that this optimization is reflected as follows[1],[2]:

Second, the multiclass Bayes error accuracy is approximated by applying this decision estimated using the adjusted kernel method over the reduced data, such that
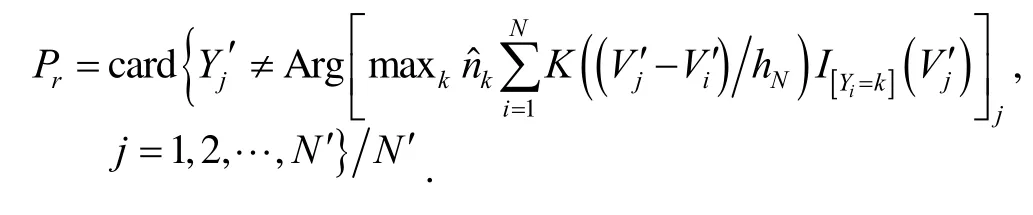
For each of these d-reducers, the misclassification rate corresponding is then estimated from a sample supervised test denoted by
The optimal smoothing parameter hNis obtained by minimizing the mean integrated squared error (MISE)according to the smoothing parameter. The well known plug-in algorithm is used to find this solution[9]. The following is the optimization algorithm of the classification system of the non-parametric optimal Bayes.
This optimization algorithm is to find a family of dimension reducersgenerated with different initializations of the numerical optimization procedure applied to the L2-PDM, and we will keep the one that minimizes the misclassification raterP:
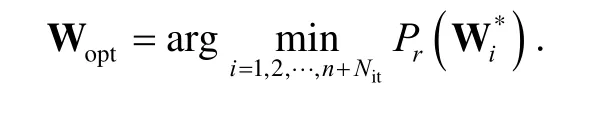
The algorithm of the proposed system BPFis shown as Fig. 1. We pass now to the analysis of the results for each of our databases (see Table 1) and the data set description is shown in Table 2, where K is the number of classes, D the data dimension, PC the data dimension after PCA, and N the size of the data. For the data set (a), we note that the error rates of the linear classifier are higher than the other classifiers, due to the fact that this classifier assumes that all the classes have the same covariance matrix. This may prove that there is indeed some separation of information present in the second order moments of the distribution of classes. Then, by applying PCA, we detected a slight improvement on the classification error rates especially when reducing to a one-dimensional space (d=1).
For the data set (b), we see that the best result obtained is that given by the proposed system, which is also given by the Bayes classifier in the original space. This can be explained by the fact that this data are close to the homoscedastic case with close mean values in every class.As a consequence, if the Bayes classifier described as the ideal is able to find the optimal error rate, then the only reducer that does not degrade this result is the proposed estimator, as it is based on the probabilistic distances. Thus,the estimator of the L2-PDM can only improve the separation of data for the classification or maintain the results of the optimal classification in the worst cases without reduction.
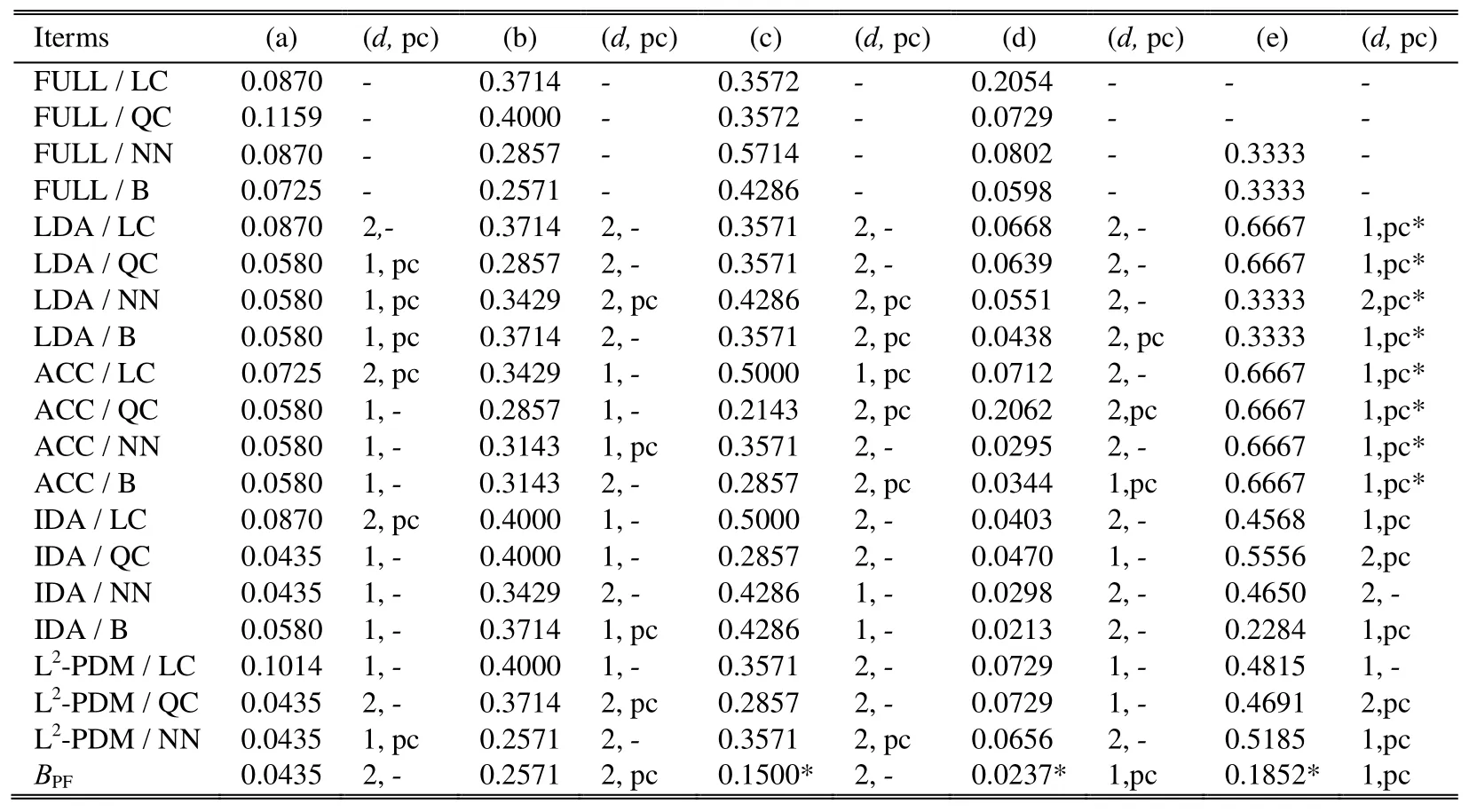
Table 1: Miss classification error by using different combinations

Fig.1.Algorithm of the proposed system.
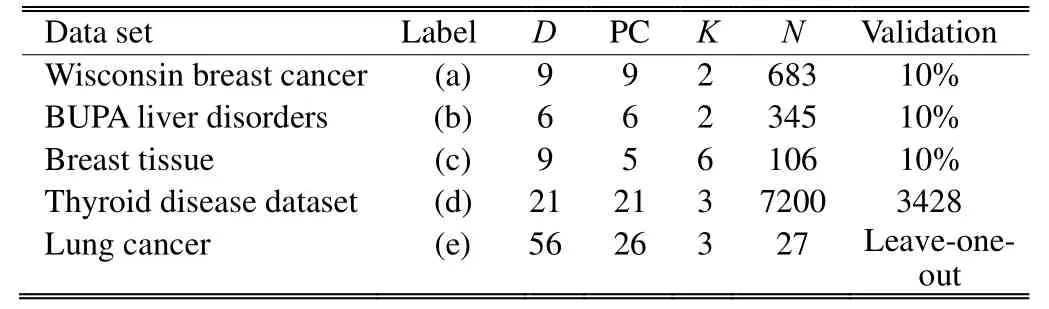
Table 2: Databases description
We can certainly note in the results of the data set (c),(d), and (e), the considerable improvement in the classification error is obtained after dimension reduction,regardless of the method involved.
Taking into account the fact that both the LDA and ACC require the calculation of the covariance matrices, the singularity problems may occur.This often happens when the data size is less than or equal to the number of primitives[10].This problem is often encountered in medical imaging; the number of patients is generally smaller than the number of primitives that are sufficient to make the diagnosis of the disease.As it is a common problem faced by many techniques, including LDA and ACC, there are a number of solutions such as the decomposition into sub-space, but the most commonly used is the removal of singularity of data through the method of PCA[11].But this problem of singularity of the covariance matrices does not figure in the case of IDA or the L2-PDM.Concerning the IDA, this approach does not directly address the covariance matrices ∑i; in contrary it is based on their representation in the transformed space T∑iTT.The major advantage of our system is that it is not limited by any assumption or condition, as the estimate of the L2-PDM is done without any assumption on the type of the distribution of the data.
Finally, the data base (e), where we can find the singularity problem (N<D), requires the application of the PCA, so we can use the reducers LDA and ACC.The best result is obtained for this database by using the system BPF,which confirms the optimality of the probability dependence measure that approximates the Bayes classifier.
4.Conclusions
In this article, we have introduced an algorithm that optimizes the maximization of the probabilistic dependence measure step to approach the Bayes classifier for high dimensions.It becomes possible by using the modified kernel estimator with the adjustment of the smoothing parameter to lower the mean integrated squared error.In order to evaluate the performance of this system, we have applied it on real world datasets, and the experiment results show the effectiveness of the proposed approach.As the perspective of this work, an asymptotic study of the discriminate analysis taking into account the information on the support of the data to be classified with these two estimators will be conducted.
[1]W.Drira and F.Ghorbel, “Nonparametric feature discriminate analysis for high dimension,” in Proc.of the 16th Ⅰnt.Conf.on Ⅰmage Processing, Computer Vision, and Pattern Recognition, Las Vegas, 2012, pp.864-868.
[2]W.Drira and F.Ghorbel, “Un estimateur de la L2mesure de dépendance probabiliste pour la réduction de dimension vectorielle pour le multi classes,” Traitement du Signal TS,vol.29, no.1-2, pp.143-155, 2012.(in French)
[3]P.M.Murphy and D.W.Aha.(2004).UCI Repository of Machine Learning Databases.[Online]Available:http://archive.ics.uci.edu/ml/citation_policy.html
[4]R.A, Fisher, “The use of multiple measurements in taxonomic problems,” Annals of Eugenics, vol.7, pp.179-188, 1936.
[5]M.Loog, R.P.W.Duin, and R.Haeb-Umbach, “Multiclass linear dimension reduction by weighted pairwise Fisher criteria,” ⅠEEE Trans.on Pattern Analysis and MachineⅠntelligence, vol.23, no.7, pp.762-766, 2001.
[6]Z.Nenadic, “Information discriminate analysis: feature extraction with an information-theoric objective,” ⅠEEE Trans.on Pattern Analysis and Machine Ⅰntelligence, vol.29, no.8, pp.1394-1407, 2007.
[7]E.A.Patrick and F.P.Fisher, “Nonparametric feature selection,” ⅠEEE Trans.on Ⅰnf.Theory, vol.15, no.5, pp.577-584, 1969.
[8]W.Drira, W.Neji, and F.Ghorbel, “Dimension reduction by an orthogonal series estimate of the probabilistic dependence measure,” in Proc.of Ⅰnt.Conf.on Pattern Recognition Applications and Methods, Vilamoura, 2012, pp.314-317.
[9]S.Saoudi, M.Troudi, and F.Ghorbel, “An iterative soft bit error rate estimation of any digital communication systems using a nonparametric probability density function,”EURASⅠP Journal on Wireless Communications and Networking, doi:10.1155/2009/512192.
[10]K.Fukunaga, Ⅰntroduction to Statistical Pattern Recognition,2nd ed.Salt Lake City: Academic Press, 1990.
[11]I.T.Jolliffe, Principal Component Analysis, Berlin:Springer Verlag, 1986.
杂志排行
Journal of Electronic Science and Technology的其它文章
- Absorption Spectrum Studies on the RDX Crystals with Different Granularity in Terahertz Frequency Range
- Classification of Diabetic Macular Edema and Its Stages Using Color Fundus Image
- Call for Papers Journal of Electronic Science and Technology Special Section on Terahertz Technology and Applications
- Terahertz Time-Domain Spectroscopy and Its Applications
- Efficient Terahertz Photoconductive Emitters with Improved Electrode Structures
- Low Power Computing Paradigms Based on Emerging Non-Volatile Nanodevices
