空腹梁上下弦肢高比对空腹式巨型框架抗震受力性能的影响
2014-12-24高荣誉熊裕林
高荣誉, 熊裕林
(安徽建筑大学 土木工程学院,安徽 合肥 230601)
0 引 言
随着高层、超高层建筑的不断发展,空腹式巨型框架结构的研究也在逐渐的深入。对于空腹式巨型框架结构与实腹式巨型框架结构的受力性能的对比已有部分研究,本文主要从空腹式巨型梁上下两肢的肢高比的不同着手,研究空腹式巨型框架结构的受力性能,从而为今后空腹式巨型框架结构的设计与施工提供参考。
1 时程分析基本理论[1]
时程分析法是对结构动力方程直接进行逐步积分求解的一种动力分析方法。采用时程分析法可以得到在地震作用下各个质点随时间变化的位移、速度和加速度,进而可以计算出构件内力和变形的时程变化[2]。下面对本文所用方法简单介绍。
Hiber-Huges-Taytor(HHT)方法:1987年休斯将Newmark-β法中的参数α进行修改,并将其导入结构的动力方程中,以后与Newmark-β方法无差别,这就是HHT法。
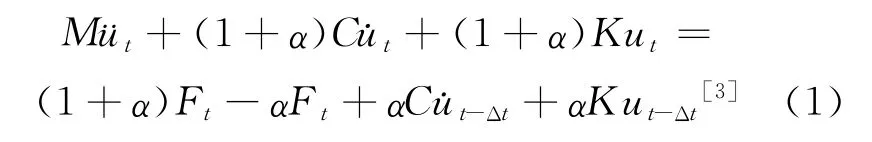
参数α在式中的取值范围为0~1/3。当α=0,此法就是Newmark-β方法当其参数α=0.5,β=0.25的情况,也就是平均加速度法,并且各种方法中最高的精度可由α=0解得,但此时会导致过多的具有与时间步长同阶或低阶周期的高频振型振动。选择负值α,此时阻尼耗散的情况较严重。通常结构为保证其收敛性,非线性分析中的α需要按负值来取得[3]。
2 空腹式[4]巨型框架的等效截面高度计算
我们可以通过相关的方法,根据刚度相等原理,将截面大小b×h的钢筋混凝土实腹式矩形截面转化为截面大小b×he(其中he为空腹式截面的高度)的钢筋混凝土空腹式矩形截面,设每肢高度分别为αhe、βhe(如下图1所示)。根据文献[5]有下式:
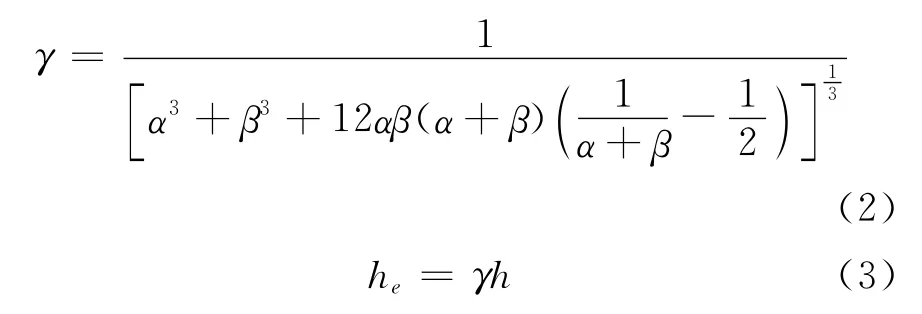
其中,α、β可以根据设计的实际需要来取值。本文在进行截面形式的换算过程中,是在保持变换前后截面的宽度b不发生变化的情况下进行的,在这种情况下,为了保持刚度不发生变化,必然会导致紧挨截面变换后的梁的上下两楼层层高发生改变,但在本文的研究中,忽略这种变化给研究带来的影响。另一方面,我们还可以在保持截面变换前后截面的高度h不发生变化,从变换截面宽度b的角度来确保刚度不变这一方向来考虑,鉴于篇幅的考虑,本文未从此角度进行相关的分析。
为了研究空腹式巨型梁上下两肢的肢高比对空腹式巨型框架结构的受力性能的影响,本文根据钢筋混凝土实腹式巨型梁(各部分尺寸见表1所示),根据空腹式等效截面的高度系数γ(如表2所示),换算成相应的空腹式巨型框架的尺寸,然后根据转换后的相应各构件的具体尺寸创建三个模型,三个模型各个构件的数据见表3所示。
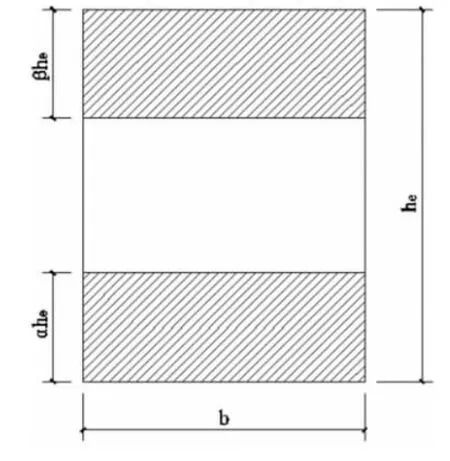
图1 空腹式截面
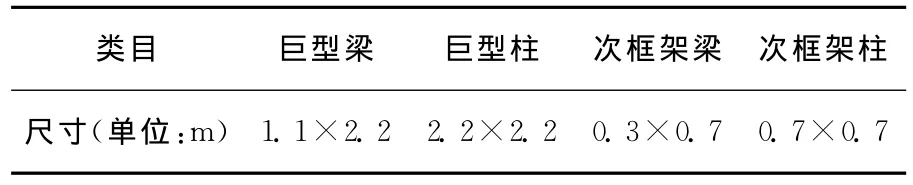
表1 钢筋混凝土实腹式巨型框架相关结构构件尺寸
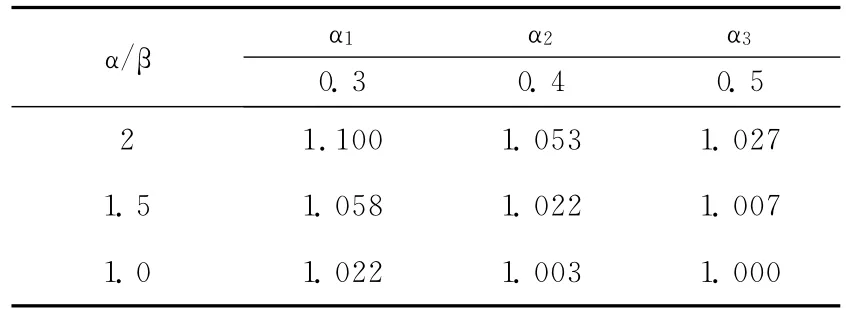
表2 空腹式等效截面的高度系数γ
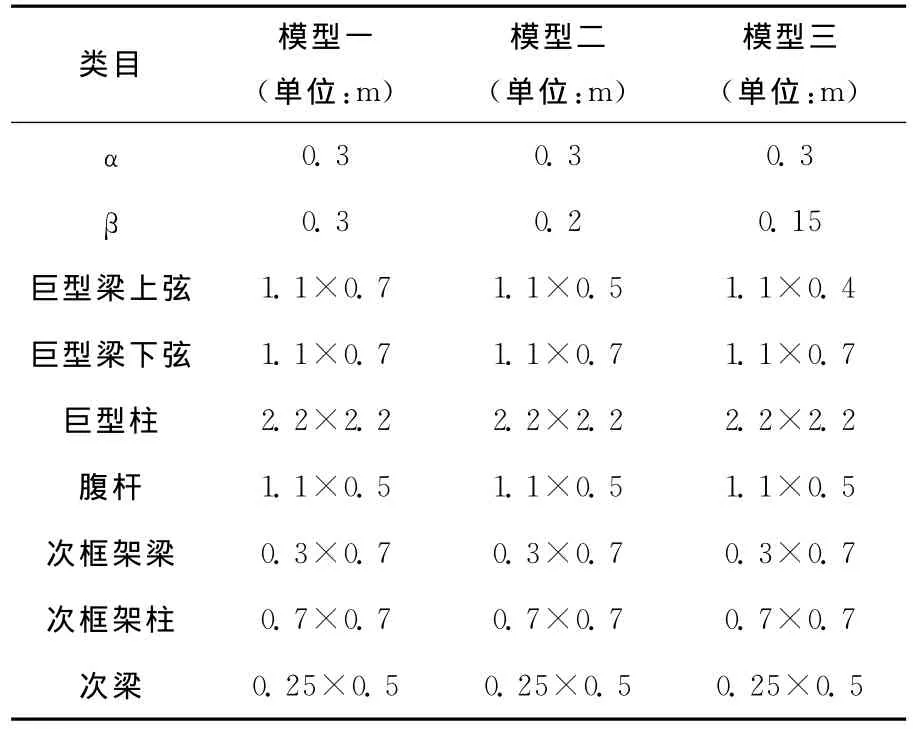
表3 三个模型空腹式截面的各部分的尺寸
3 巨型框架结构受力性能分析
3.1 建立结构模型
为了研究空腹式巨型梁上下两肢的肢高比对空腹式巨型框架受力性能[6]的影响,现建立三个模型。模型均取24层,高度100.8m,空腹式巨型梁柱采用C60级混凝土强度,次框架柱采用C40采用混凝土强度,结构构件的具体数据见上表3所示。
荷载取值按照《建筑结构荷载规范(GB 50009-2012)》中办公楼采用并稍加修改,具体设置荷载如下,楼面恒载2.0KN/m2,楼面活载341.7cm/s2,屋 面 恒 载 3.5KN/m2,屋 面 活 载0.5KN/m2,为了考虑填充墙在地震下的作用,在所有楼面边梁上施加一个6KN/m均布线荷载。模型一、模型二和模型三都设置三根主框架梁,位置在第8层、第16层、第24层。如图2所示。

图2 分析模型
设计使用年限50年,地震设防烈度为7度,设计其本地震加速度值为0.10g,Ⅱ类场地土,设计地震分组为第一组Tg=0.35s,根据建筑设计抗震规范规定,采用时程分析法时所用地震加速度时程的最大值:多遇地震时为35cm/s2,罕遇地震时为220cm/s2[7]。
3.2 模态分析
根据模态分析的结果,三个空腹式巨型框架结构的前12阶自振周期见下表4所示。
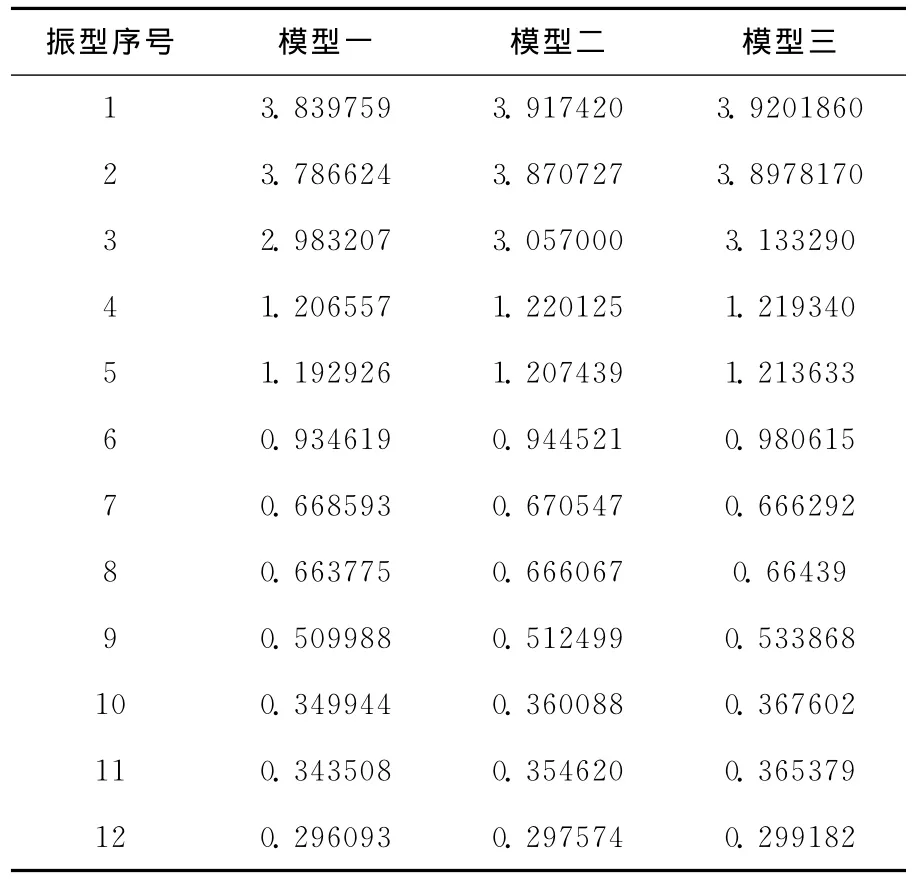
表4 空腹梁的上下弦肢高比变化模型自振周期对比(s)
根据上表数据可以做出下图3。
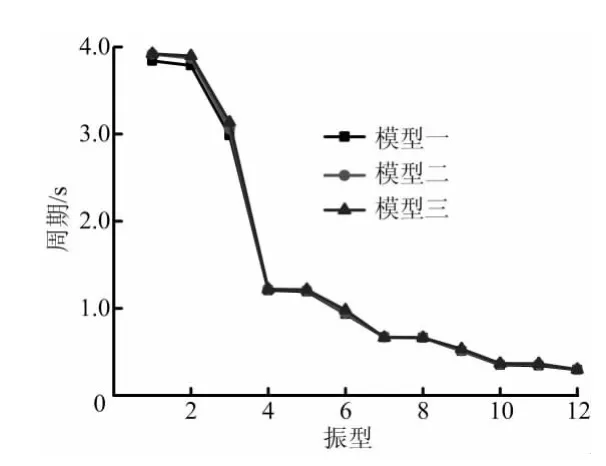
图3 空腹梁的上下弦肢高比
图3给出了不同方案模型的自振周期的对比图形,图中显示出了三种不同肢高比的空腹梁的各自前12阶自振周期,从图中我们可以得到三种模型自振周期的变化规律:模型的自振周期随着空腹梁上下弦肢高比的变化而发生变化,但由于上下弦肢高比的变化不大,自振周期的变化不是十分的剧烈。具体变现为,随着空腹梁下弦与上弦高度比的增大,模型的自振周期呈现相互逐渐变大的趋势。三种模型在前五阶振型变化较为剧烈,但在五阶以后,递减变得较为平缓。
3.3 结构动力弹性时程分析
对模型一、模型二、模型三分别采用El-centro地震波(El-centro地震波加速度曲线见图4),时程计算时间为30s,时间间隔为0.02s,其峰值加速度为341.7cm/s2;Taft地震波,时程计算时间为30s,时间间隔为0.02s,其峰值加速度为175.9cm/s2;Lanzhou地震波,时程计算时间为20s,时间间隔为 0.02s,其峰值加速度为196.2cm/s2。
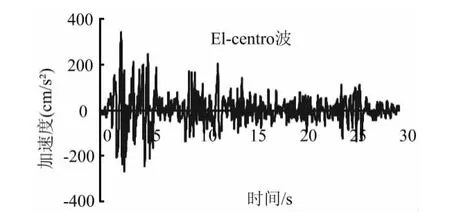
图4 El-Centro波加速度曲线
经过时程研究分析,我们可以得到模型一、模型二、模型三分别在El-centro地震波、Taft地震波、Lanzhou地震波作用下的结构楼层侧移、层间位移角、顶层位移、基底剪力。这里为简便起见,这里只给出模型一、模型二、模型三在Elcentro地震波作用下结构楼层侧移、层间位移角、顶层位移、基底剪力,分别见图5、图6、图7、图8所示(图5纵轴表示楼层侧移,单位mm,横轴表示楼层层数;图6纵轴表示层间位移角,单位10-3rad,横轴表示楼层层数;图7纵轴表示基底剪力,单位KN,横轴表示时间,单位s;图8纵轴表示顶层位移,单位mm横轴表示时间,单位s)。?
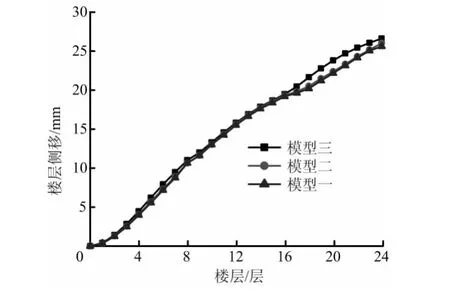
图5 El-centro波下不同方楼层侧移对比图
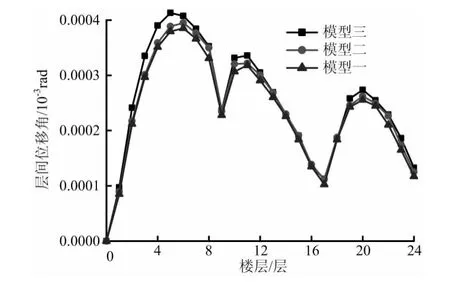
图6 El-centro波下不同方案层间位移角对比图
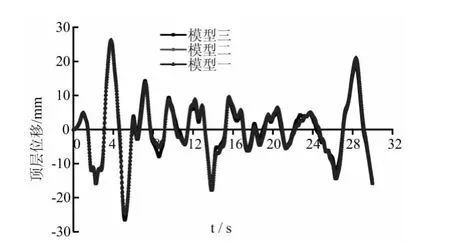
图7 El-centro波下不同方案顶层位移对比图
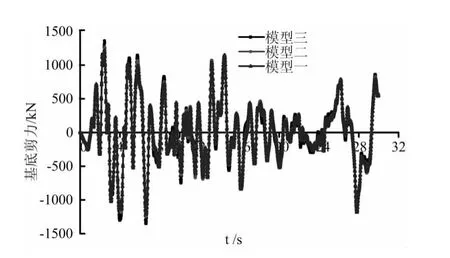
图8 El-centro波下不同方案基底剪力对比图
根据以上的相关分析,综合模型一、模型二、模型三在El-centro波、Taft波、Lanzhou波下相关数据列表如下:
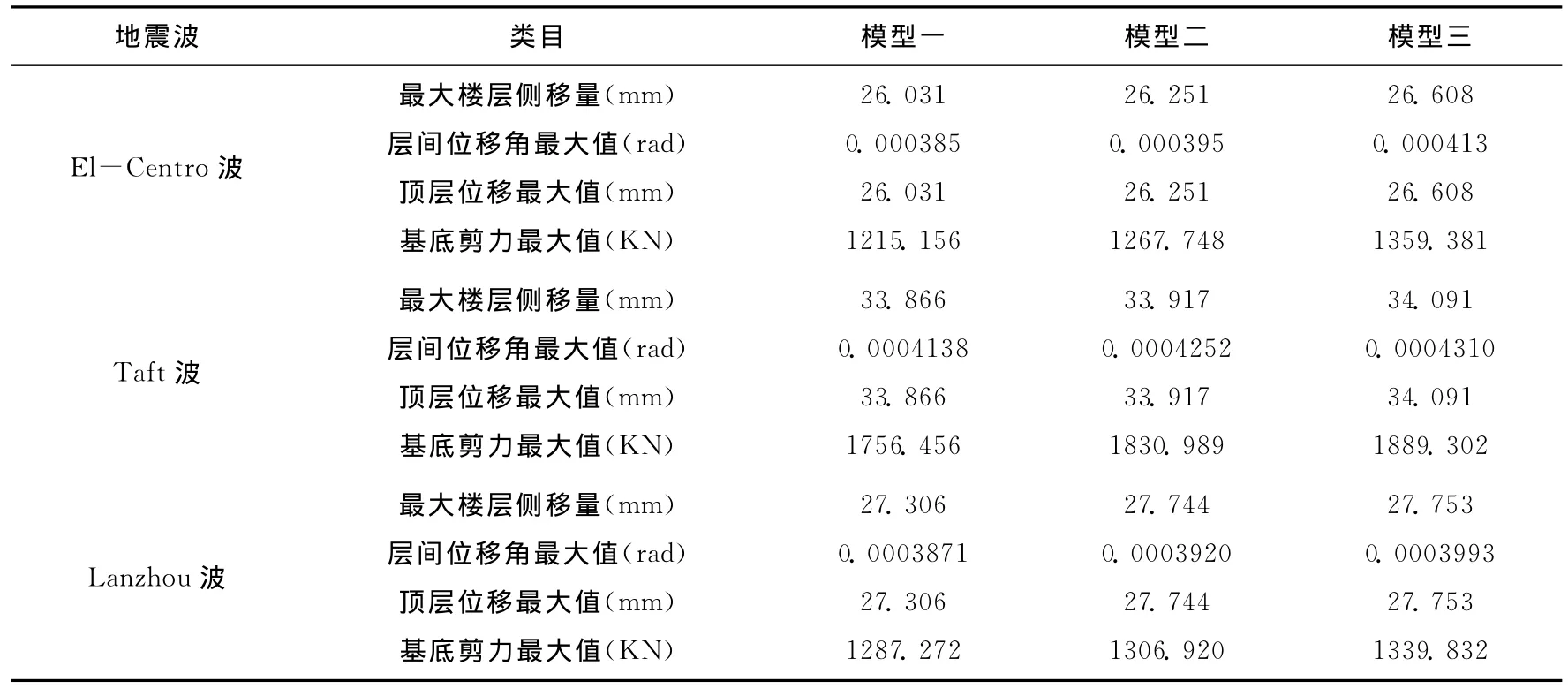
表5 三种模型在三种地震波下的相关数据对比
3.4 结构动力弹塑性时程分析
为简便起见,本文以空腹式巨型框架模型三为例,对其进行动力弹塑性时程分析,下图给出了模型三在El-centro波下动力弹塑性时程分析的相关数据和图表(如图9-12,表6)。
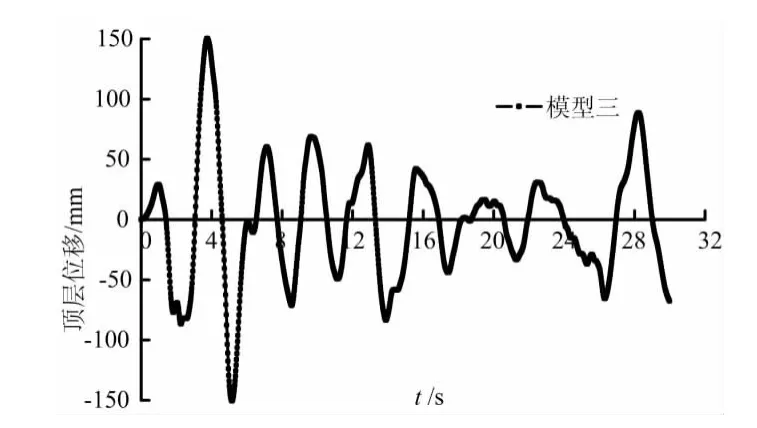
图9 El-centro波下顶层位移图
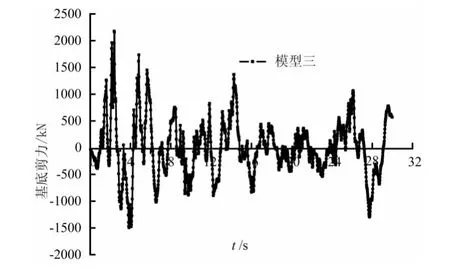
图10 El-centro波下基底剪力图
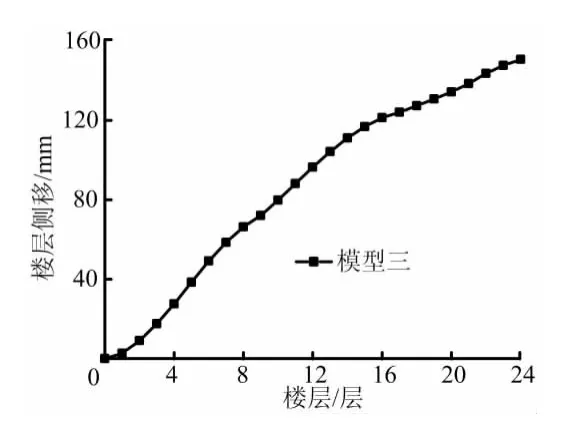
图11 El-centro波楼层侧移图
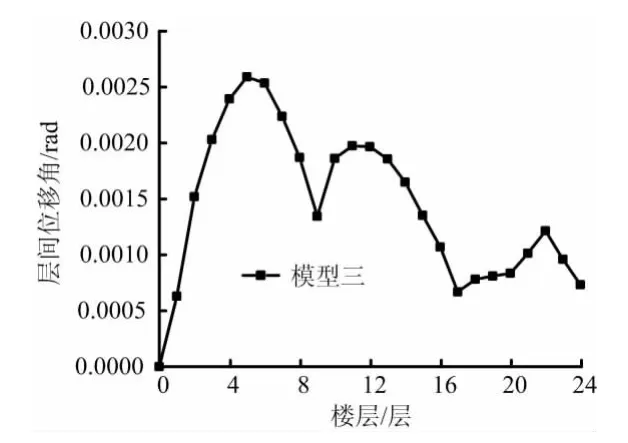
图12 El-centro波层间位移角图
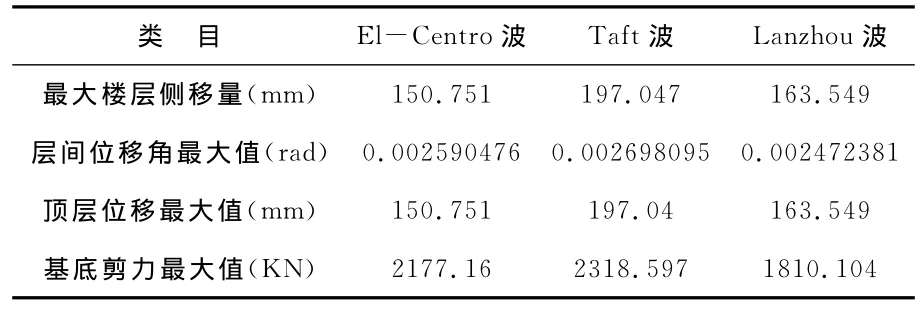
表6 模型三在三种地震波下动力弹塑性时程分析数据
在El-centro波、Taft波、Lanzhou波地震波作用下,结构会出现塑性铰。下图13给出了模型一塑性铰发展情况。
由图可知,在El-centro地震波作用下,塑性铰按一定的次序出现:第一次出现塑性铰实在1.54s。结构首先出现塑性铰的部位在结构的下部,由下往上发展,首先出现在次框架梁端,紧接着出现在空腹梁端,随着梁端塑性铰的不断发展,次框架柱端开始出现塑性铰,主框架柱不会出现塑性铰。
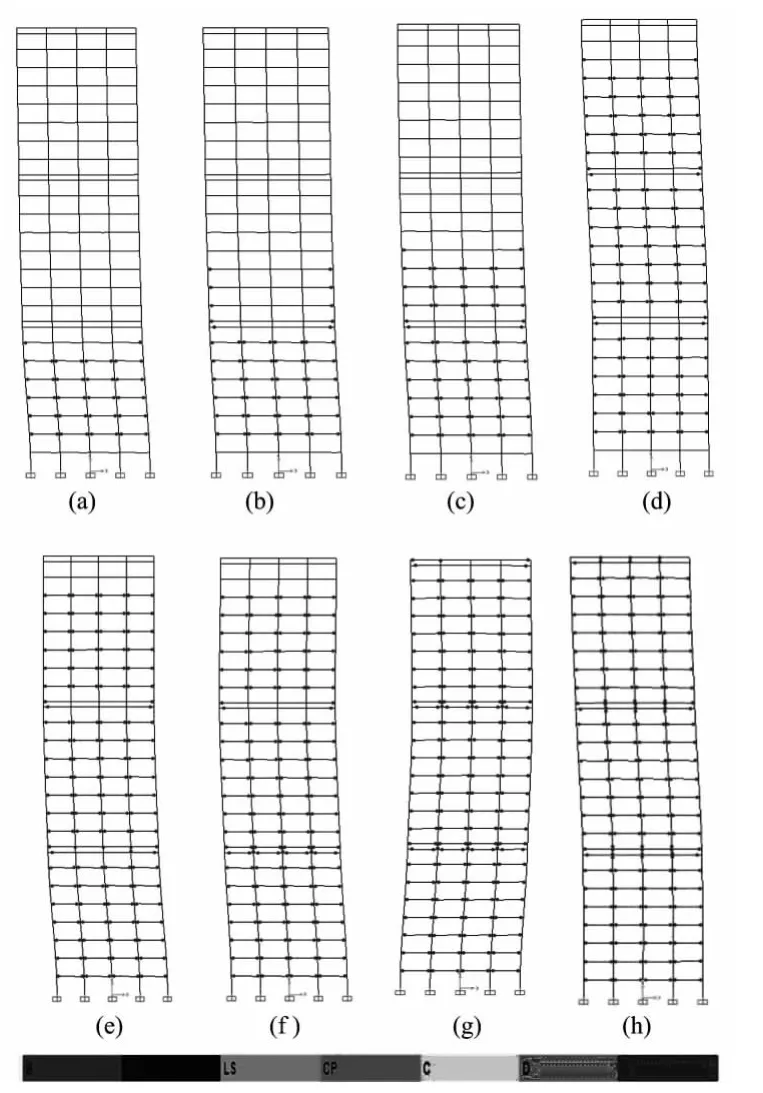
图13 El-centro波下模型三塑性铰发展情况
4 结 论
经创建模型并进行相关分析可得出:
1、在El-centro波、Tafa波、Lanzhou波作用下,模型一、模型二、模型三的最大层间位移角均小于抗震规范《建筑抗震设计规范(GB50011-2010)》规定的钢筋混凝土框架弹性层间位移角限值1/550[7]的限值要求。以结构在El-centro波作用下为例,模型一、模型二、模型三的最大层间位移 角 分 别 为 0.000413rad,0.000395rad,0.000385rad,模型二比模型一的最大层间位移角减少4.4%,模型三比模型二的最大层间位移角减少2.5%。
2、模型一、模型二、模型三在El-centro波作用下的基底最大剪力分别为1359.381KN,1267.748KN,1215.156KN;模型二比模型一的最大层间位移角减少7%,模型三比模型二的最大层间位移角减少4%。
3、模型一、模型二、模型三在El-centro波作用下的楼层侧移最大值分别为26.608mm,26.251mm,26.031mm;模型二比模型一的最大层间位移角减少1.3%,模型三比模型二的最大层间位移角减少0.84%,减少比率较小。
4、模型二比模型一的截面面积少14.3%,即节约建筑材料14.3%;模型三比模型二的截面面积少8.3%,即节约建筑材料8.3%。
5、通过对空腹式巨型框架结构的动力时程分析,可知:空腹式巨型框架的受力性能符合GB50011-2010建筑抗震设计规范里面相关的规定;并且,空腹式巨型框架结构在罕遇地震作用下,出铰合理,出铰顺序符合相关的设计要求。
在三种不同的地震波作用下,即便是同一建筑模型的在地震下的反应也不尽相同;在相同的地震波作用下,不同建筑结构模型在地震波下所得到的结果也相差较大。
1 高荣誉,汤 薛.巨型框架主框架梁均匀布置动力时程分析[J].安徽建筑工业学院学报,2012,20(1):1-3.
2 熊裕林,高荣誉.实腹式巨型框架与空腹式巨型框架抗震受力性能对比研究[J].安徽建筑工业学院学报,2014,22(2):29-32.
3 北京金土木软件技术有限公司,中国建筑标准设计研究院.SAP2000中文版使用指南(第2版)[M].人民交通出版社,2012:313-314.
4 沈蒲生.巨型框架结构设计与施工[M].北京:机械工业出版社,2007:15-22.
5 熊裕林,空腹式钢筋混凝土巨型框架抗震受力性能的研究[D].合肥:安徽建筑大学土木工程学院,2014.
6 林 倩.巨型框筒结构的动力特性研究[D].南宁:广西大学土木工程学院,2005.
7 GB50011-2010,建筑抗震设计规范[S].北京:中国建筑工业出版社, .
