基于GAIS-BP网络在故障诊断中的应用
2014-12-23佘喜萍田玉玲
佘喜萍,田玉玲
(太原理工大学 计算机科学与技术学院,山西 太原030024)
0 引 言
目前在网络故障诊断技术的研究工作中,人工神经网络 (ANN)的应用最为普遍,但该算法存在一些缺点,通过积极吸取国外先进理念和技术,来提高网络领域的智能诊断技术。
在人工神经网络模型中,BP网络是一种特殊的多层感知机,通常采用梯度下降法迭代优化权值来减小误差函数,将网络实际输出与目标输出的均方误差 (MSE)定义为误差函数。但是,梯度下降法也有一些不足之处,如:局部最优,对权值的初值敏感,不能处理非微误差函数[1]。
为了克服这些缺点,在过去几十年已经用计算智能技术方法进行训练权值,尤其在生物启发算法领域,如遗传算法、蚁群优化算法、粒子群优化算法、分布估计算法和人工免疫算法。这些算法基于种群搜索策略,能够成功处理复杂而庞大的搜索空间。
在这些算法中,人工免疫系统 (AISs)的特性被广泛地利用,即:种群大小的动态控制;探测或开发搜索空间的有效机制,能够发现和保存局部最优,并且采样和随机插入新个体能够保持种群多样性[2]。
尽管在解决一般问题上表现出高性能,但是也有许多免疫启发算法共有的缺点:随着问题规模和复杂度的增加,算法的性能与适当选择设计参数密切相关,如变异率。
为弥补AISs的缺点,研究者们提出采用概率模型来实现高性能的人工免疫系统。基于该思想,已经改进一些算法并且成功应用于不同优化问题上。例如:贝叶斯人工免疫系 统 (BAIS)[3]和 多 目 标 贝 叶 斯 人 工 免 疫 系 统(MOBAIS)[4],在离散域分别对应单目标和多目标优化,高斯 人 工 免 疫 系 统 (Gaussian artificial immune system,GAIS)[5]和多目标高斯人工免疫系统 (MOGAIS)[6]在连续域分别对应单目标和多目标优化。这些算法不仅能够处理构造模块而且有着上述AISs的优点。
本文提出采用GAIS算法训练BP网络的权值和偏差来解决连续域中的单目标问题。由于高斯网络能够正确捕捉变量之间的关系,因此,本文利用高斯网络概率模型。
1 GAIS
近年来提出用免疫启发算法来解决连续优化问题,概率模型替代变异和克隆操作来产生新抗体。由于高斯网络能够极大地表示变量之间的关系,本文中的算法采用高斯网络,故称之为高斯人工免疫系统 (GAIS)。该算法用一个候选解集 (抗体)实现,这样的解集能够根据问题增加或减小。
GAIS算法如下:
(1)初始化抗体种群;
(2)种群估计;
(3)选择最佳抗体;
(4)每迭代p 次建立一个高斯网络;
(5)采样新抗体;
(6)抑制亲和力小于阈值的抗体;
(7)消除相似抗体;
(8)随机插入新抗体;
(9)如果不满足停止条件,则返回 (2),否则,算法结束,得出最优解集。
GAIS中,随机产生初始种群。从当前种群挑选最佳解(抗体),根据这些抗体建立高斯网络。从网络中采样一些新抗体插入到种群中,消除相似的和亲和力低的抗体。为保持种群多样性,随机生成少量抗体并插入到种群中,更好地搜索种群空间。
为了减少计算代价、降低运行时间,每p 次迭代重建网络结构 (p>1),每迭代一次重新计算网络的联合概率。
GAIS不仅保持种群多样性,还实现多峰优化,根据待解问题动态调整种群大小,最重要的特性是,能够识别和处理构造模块。该算法就同一问题运行多次后,搜索过程更具鲁棒性。此外,候选解大量减少直到BP网络达到某一性能水平。
该算法中提到两个方法,一个是根据选出来的抗体建立高斯网络 (即:高斯网络的学习);另一个是如何利用高斯网络产生新抗体。
1.1 高斯网络——学习和采样
GAIS最基本的两个任务是高斯网络的学习和采样。对于一个给定的潜在解集,学习高斯网络,相当于估计它们的联合分布。根据已建立的高斯网络采样新实例作为新候选解。
高斯网络是概率图模型,通常用于连续域,来估计变量的概率依赖性[7]。高斯网络通常用一组变量集合X={X1,X2,…,Xn}表示,它是有向非循环图,节点表示问题的变量,边表示变量之间的依赖关系。图1 表示有5个变量的高斯网络。
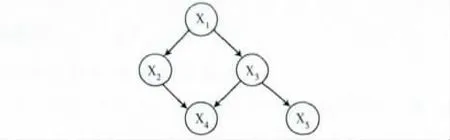
图1 变量个数为5的高斯网络
图1中5个变量的联合概率
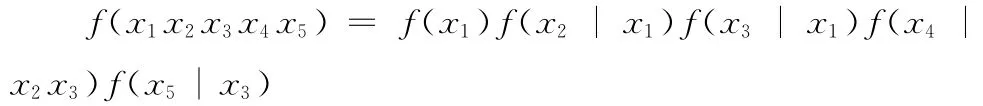
X 的联合概率由n 维高斯分布表示,故称之为高斯网络
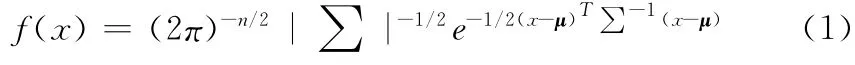
例如,如果节点X1到节点X2有一条边,那么称X1是X2的父节点,所以X2的值条件依赖于X1的值。如果Xi有一系列父变量pai,它的概率分布是由条件概率密度函数 (PDF)决定,表示为f(Xi|pai)。另外,没有父变量的节点Xj的概率分布用无条件概率密度函数f(Xj)表示。所以,X 的联合概率分布由条件概率密度函数表示,每个密度函数是一个独立的高斯分布
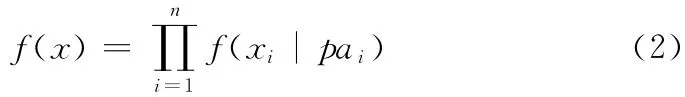
式中,μi 是Xi的均值,σ2是Xi条件依赖于Xi父节点的方差,bki是线性系数,表示Xk与Xi之间的连接强度。如果bki=0,那么Xk与Xi之间没有联系。
将高斯网络中的bki和σ2i表示精度矩阵W,通过下列递推公式得到等价的高斯分布[8]
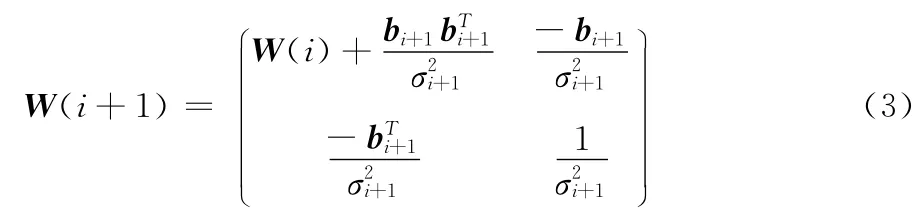
1.2 学 习
高斯网络从数据集中的学习过程如下:首先给定一批观察数据,搜索网络中满足条件的网络并计算网络得分,最高得分的网络模型表示这些数据的联合分布。通过搜索和评分方法学习的网络来提供图的结构,也就是估计每个变量的概率分布。
学习高斯网络的通用方法是,给定的一个可以提供到空间中每个节点的相对得分的矩阵,采取一种用于搜索所有可能的候选网络结构空间的程序。GAIS 采用启发式搜索,初始网络为只有节点没有边的网络;用数据集估计每个变量的概率分布并计算网络得分。建议搜索过程中通过增加、删除一条边,或转换边的方向来改变图的结构,以便获得比之前有更高得分的网络。每次更改图的结构之后计算网络变量的概率分布。而高斯网络的得分矩阵,GAIS采用贝叶斯信息准则 (BIC)计算[9]
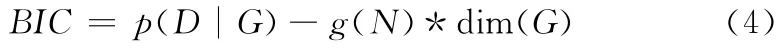
其中
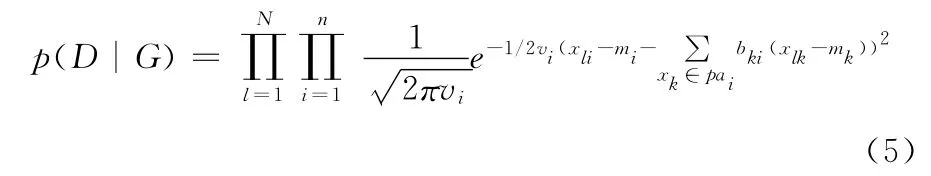
D 表示数据集,G 是被估计的网络,N 是实例数,n是变量数,bki是Xk和Xi的线性系数,pai是Xi的父节点集,vi是Xi的 条 件 方 差,存 在X1,…,Xi-1i,k。函 数是惩罚复杂模型的函数,dim(G)=2n+是被估计参数的个数。
1.3 采 样
一旦建立高斯网络,利用高斯网络编码的联合概率分布 (式 (1))产生新实例。本文在高斯网络中使用一种寻找节点祖先顺序的方法,一次实例化一个变量,也就是,直到该变量所有的父节点被采样之后,它才被采样。GAIS中,采样实例的数目随时间变化。
2 GAIS学习BP网络的权值和偏差
为证明GAIS 训练BP 网络权值的有效性,在这一部分,主要介绍分类问题,BP网络的拓扑结构采用完全连接的标准BP网络,即只有3 层。图2 描述了GAIS训练BP网络权值用于网络故障诊断的过程。首先,将数据集归一化,并分为两类数据:训练样本和测试样本。训练样本送入GAIS中进行学习,而测试样本直接送入训练后的BP模型中进行检测。
2.1 编 码
由于BP网络的误差函数由权值和偏差构成的,训练网络变成了一个搜索最佳权值和偏差的问题,而最佳权值集要有最小的误差。抗体是实数编码向量,由BP 网络输入层、隐藏层和输出层的个数决定抗体的长度。
2.2 初始化种群
GAIS中的初始种群是用均匀分布编码,随机生成数值在 [-0.5,0.5]的矩阵。
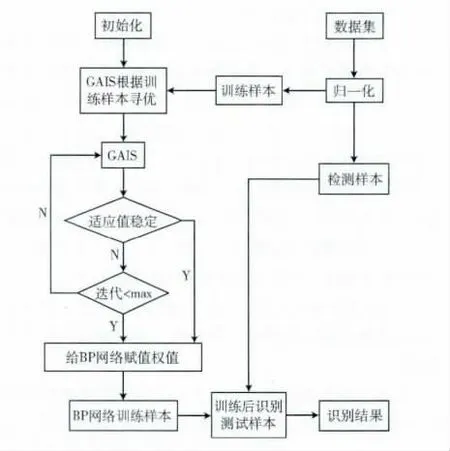
图2 GAIS训练BP权值的故障诊断方法
2.3 适应度函数
适应度函数基于BP网络性能定义,引用一个能正确分类训练模式数目的函数计算。适应度函数可表示为

其中,NPCC (Abi)是网络对抗体Abi编码的正确分类模式的数目,NP 是训练集的实例总数。
2.4 抑 制
此阶段,消除相似抗体来避免冗余、保持多样性。
初步实验表明,抑制机制依赖于待解决问题的维数,即待调整的权值和偏差数量。因为抑制机制采用解之间的欧氏距离,对于规范化向量,维数越大,距离越大。由于要研究的问题需要不同的神经网络维数,与参数抑制独立有关。以下步骤实现抑制:
(1)权值向量规范化为 [0,1]区间的值;
(2)确定规范化解的欧氏距离阈值ε;
(3)通过阈值将欧氏距离小于ε的抗体从种群中移除。
3 实验结果与分析
本文引用广泛应用于机器学习的6 种分类数据集和NS2模拟网络数据集,分别对GAIS-BP 网络和GA-BP 网络[10,11]两种算法进行对比及分析。
3.1 实验方法
实验中六种数据集使用的参数一致。GAIS初始种群包含50个抗体,最大的迭代次数作为算法的终止条件,这里定义为500。
GAIS算法与GA 算法分别学习BP 网络的权值。GABP是用遗传算法优化BP网络的权值,遗传算法采用选择、交叉、变异、克隆等免疫操作。
对于GAIS,每迭代10次建立高斯网络,但是每迭代一次更新网络的概率。为惩罚模型的复杂度,对一个节点能拥有父节点的个数加一个约束。相当于一个可以覆盖最大相互作用的顺序,并且直接影响模型的复杂度。通过对高斯网络学习的初步实验,我们知道网络复杂度越高,越有可能检测出数据间伪相关性。因此,每个变量只能有两个父节点。对于GAIS,当前种群个数的80%用于建立概率模型。产生样本的数量是当前种群大小的一半。为产生多样性,插入到种群的随机个体数大约是当前种群大小的3%。
GAIS使用概率模型,GA 不包含概率模型,因为高斯对非高斯的免疫启发算法,所以采用这两种算法对比是有道理的。
算法的参数通过初步实验调整。两种算法使用相同的神经网络拓扑结构,见表1的第5列。
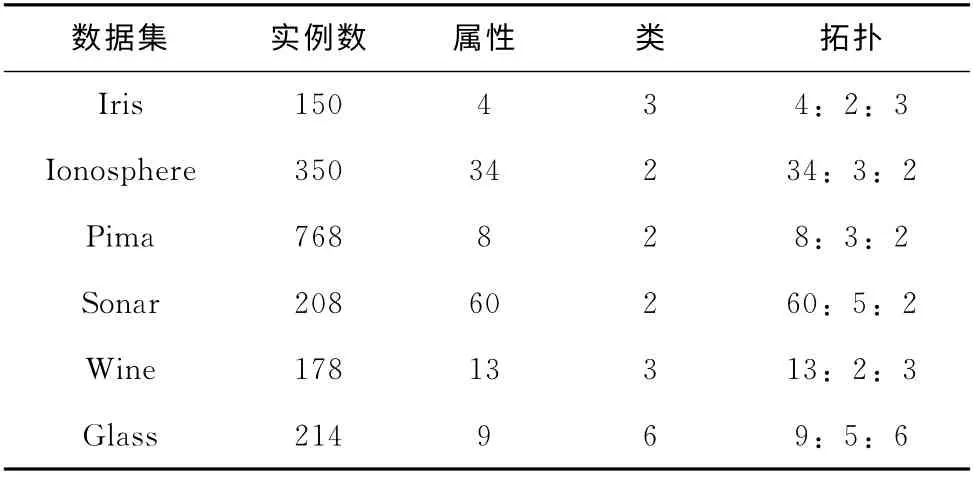
表1 数据集的特性
3.2 UCI数据集
3.2.1 描述数据集
我们采用UCI标准数据集中的六种数据集:Iris、Ionosphere、Pima、Sonar、Wine、Glass。表1 给出每组数据的特性,包括实例总数、属性数量、分类数和网络的结构(输入数,隐藏神经元数和输出数)。考虑每个数据集的初步实验的基础上确定隐藏层神经元的数目。所有数据的属性规范化到 [-1,1]范围内。
3.2.2 实验结果
实验中把数据集分为训练样本和测试样本,其中80%的数据集作为训练样本,剩下的20%作为测试样本。
从表2中可以看出所有算法对测试样本检测的正确率都低于训练样本,因为测试数据集是未知数的数据,在六组分类数据集上表现出较高的泛化能力。由于GA 算法的变异操作不能捕捉变量之间的关系,故GAIS算法的正确率高于GA 算法。从搜索过程可以看出,GAIS随着种群的大小动态地增减。实验中,GAIS在单次运行中能产生几个不同高质量的神经网络。此外,在相对较短的迭代次数中能得到最优解。表明识别和保存构造模块与执行多峰搜索的能力一样,使算法收敛速度更快。
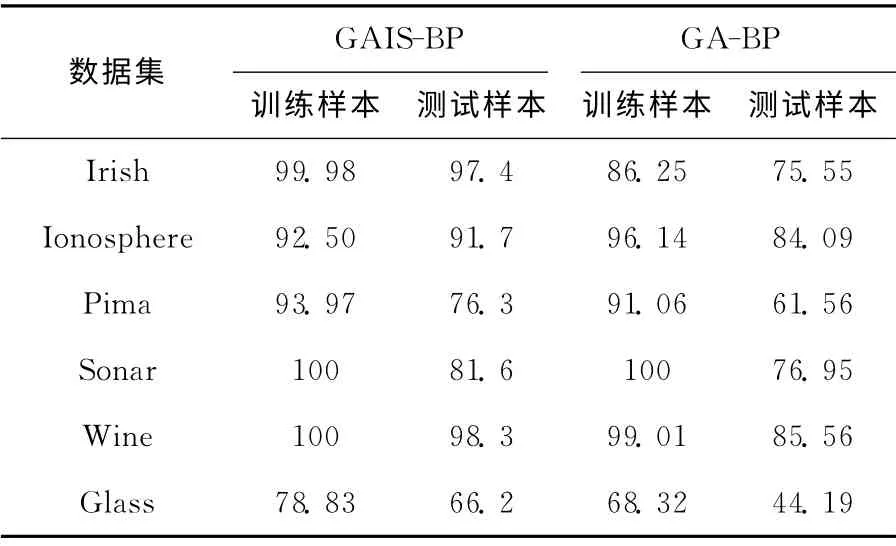
表2 测试数据集的正确率 (%)
3.3 网络实测数据集
3.3.1 描述数据集
以NS2仿真软件对某网络仿真的实测数据进行验证。网络拓扑如图3所示。
图3 实验网络拓扑图
NS2的模拟仿真图如图4所示。

图4 NS2仿真结构
对核心交换机相连的3个子网端口及与路由器相连端口平均输出、输入流量,CRC校验错,丢包率,端口协议,端口管理状态,端口当前状态,端口检测数据进行采集,采样间隔为10s,获得5000条样本数据,每个样本包含10个属性。取其中对故障状态有较大影响的3个属性 (即端口管理状态、端口当前状态、端口检测)进行预处理。实验过程中人为设置链路通断状态及网络阻塞等故障现象。由于每组数据有10个属性,隐含层节点数根据经验得出,输出结果有已知故障4 种:适配器故障、物理链路故障、管理性关闭、协议故障和未知故障、正常数据共6 类,故其神经网络拓扑结构为10:3:6。
3.3.2 实验结果
GAIS随机选择80%的数据作为训练数据。采用抑制机制消除相似网络。实验结果见表3。
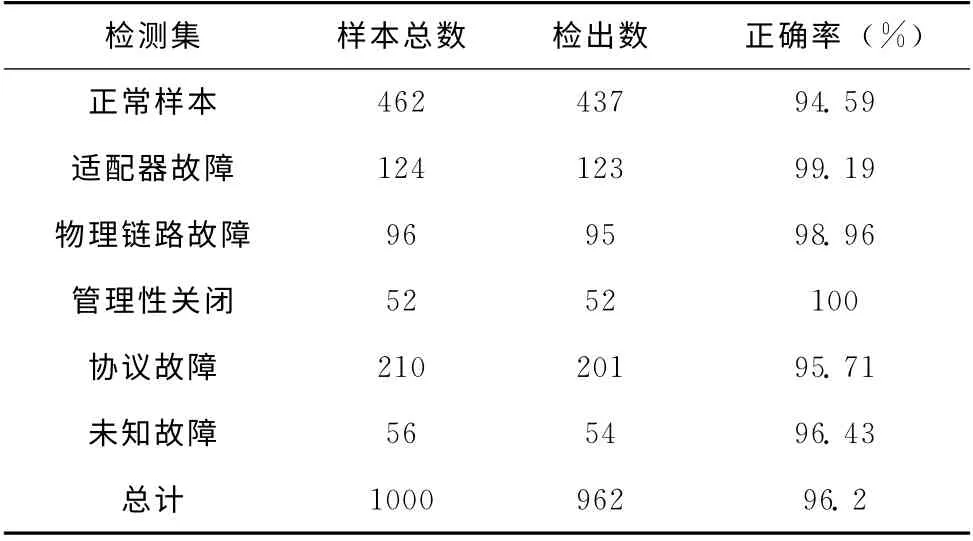
表3 网络故障实验结果 (测试样本)
从实验结果中可以看出,正常样本和协议故障有重叠导致了正确率偏低,由于未知故障是未确定的类,不能很快确定其故障类型,其它类的故障的识别率都达到了满意值,本文提出的方法在实测网络数据上的正确率可以满足实际网络故障检测的需要。
4 结束语
网络故障诊断中,算法的运行时间及检测故障的正确率是网络管理系统评价一个方法是否有效的两个性能指标。本文提出将利用采用概率模型的GAIS 来优化BP 网络权值,提高了收敛速度并能识别和保存构造模块,与遗传算法相比减少了运行时间,提高了正确率。在UCI数据集和网络实测数据集的实验结果中可以看出,GAIS-BP 和GABP算法的运行时间随着数据维数的增加而增加。实验表明,GAIS设计精确网络分类模型,并根据该模型的性能产生更好的结果。
尽管取得满意结果,但仍然还有一些需要进一步完善的地方,比如,评估高斯网络的方法、采样新个体的方法。
[1]HOU Rui.Introductions and applications of BP artificial neutral network [J].Science & Technology Information,2011,30(3):75-418 (in Chinese).[侯瑞.人工神经网络BP算法简介及应用 [J].科技信息,2011,30 (3):75-75.]
[2]Al-Enezi J R,Abbod M F,Alsharhan S.Artificial immune systems-models,algorithms and applications [J].International Journal of Research and Reviews in Applied Sciences,2010,3(2):118-131.
[3]Castro P A D,Von Zuben F J.Learning ensembles of neural networks by means of a bayesian artificial immune system [J].IEEE Transactions on Neural Networks,2011,22 (2):304-316.
[4]Castro P A D,Von Zuben F J.Multi-objective feature selection using a Bayesian artificial immune system [J].Journal of Intelligent Computing and Cybernetics,2010,3 (2):235-256.
[5]Castro P A D,Von Zuben F J.GAIS:A gaussian artificial immune system for continuous optimization [R].Australia:Proc 9th Int Conf on Artificial Immune Systems,2010:171-184.
[6]Castro P A D,Von Zuben F J.A gaussian artificial immune system for multi-objective optimization in continuous domains[R].USA:Proc 10th International Conference on Hybrid Intelligent Systems,2010:159-164.
[7]LI Bin,ZHONG Runtian,WANG Xianji,et al.A continuous optimization algorithm based-on progressive estimation of gaussian mixture model[J].Chinese Journal of Computers,2007,30 (6):979-985 (in Chinese).[李斌,钟润添,王先基,等.一种基于递增估计GMM 的连续优化算法 [J].计算机学报,2007,30 (6):979-985.]
[8]Prakash P Shenoy.Inference in hybrid Bayesian networks using mixtures of Gaussians[R].USA:Twenty-Second Conference on Uncertainty in Artificial Intelligence,2012:428-436.
[9]XU Jinchao,ZENG Guosun,WANG Wei.Software reliability assessment based on Bayesian method [J].Journal of Tongji University (Natural Science),2012,40 (7):1102-1110 (in Chinese).[许金超,曾国荪,王伟.一种基于贝叶斯理论的软件可靠度评估方法 [J].同济大学学报 (自然科学版),2012,40 (7):1102-1110.]
[10]XIAO Zhiping,WU Wenquan,ZENG Yang.Research on application of GA-BP neural networks is fault diagnosis of airborne radar[J].Computer Measurement & Control,2011,19 (1):14-16 (in Chinese).[肖治平,吴文全,曾洋.遗传BP网络在机载雷达故障诊断中的应用研究 [J].计算机测量与控制,2011,19 (1):14-16.]
[11]NONG Jifu.Precipitation forecasting model based on neural network and genetic algorithms [J].College Mathematics,2012,28 (5):114-118 (in Chinese).[农吉夫.遗传算法与神经网络结合的降水预报模型 [J].大学数学,2012,28(5):114-118.]
