基于改进粒子群优化的车辆自适应巡航控制
2014-12-23赵法信金义富
张 强,赵法信,金义富
(湛江师范学院 信息科学与技术学院,广东 湛江524048)
0 引 言
车辆自适应巡航控制 (adaptive cruise control,ACC)是一种车辆辅助系统,可以增强道路安全性和乘客的舒适度。由于系统的非线性和动态切换,以及存在的限制使得设计ACC存在很多挑战,传统的控制技术已经不适用[1]。
模型预测控制 (model predictive control,MPC)在多种系统建模方法中具有重要地位,如为混合系统建立模型[2],但是MPC在线优化过程中因需要大量的计算而不适合在需要频繁采样的ACC系统中使用[3]。近年来,学者为降低计算时间提出很多方法。文献 [4]提出离线计算即显示MPC,但是显示MPC 限制在相对小的问题规模中 (典型1~2个输入,至多8个状态)[5]。为了处理大规模的混合系统,文献 [6]提出混合模型预测控制 (hybrid model predictive control,HMPC),并且设计混合系统描述语言(hybrid systems description language,HYSDEL)为开环系统的切换和受限建模,自动将模型转换成一系列线性等式和不等式。混 合 整数线性 规 划 (mixed integer linear programming,MILP)是基于线性等式和不等式组的无限优化控制,一些元素必须等于0或1。在公共领域MILP问题求解器有GNU (gnu's not unix)线性编程工具GLPK (gnu linear programming kit),商 用 混 合 整 数 规 划 软 件 有CPLEX[7]。
随着人工智能的发展,开始在MPC 中引入智能算法。Susuki等人利用粒子群优化算法 (particle swarm optimization,PSO)调整MPC的参数[8]。Na等人设计了一种基于PSO 的模型预测控制器[9]。标准PSO 适用于优化非凸连续问题,因此在混合或者离散问题中使用PSO 时,设计变量都应该作为连续变量来处理,也就是要将离散的设计变量通过一些方法转换成连续变量[10]。
针对ACC 系统计算时间过长问题,将多目标优化(multi-objective optimization,MOO)技术引入到标准PSO算法中,如Pareto 支配[11],提出一种改进的粒子群优化(modified particle swarm optimization,MPSO)算法。MPSO 基本思想:利用HMPC 为ACC 建立混合模型;采取HYSDEL将模型转换成MILP问题;将MILP 问题转换成MOO 问题,利用MPSO 算法在线求解MILP问题;最后利用优化得到的控制序列作用于巡航车辆,自适应改变车辆的速度。
1 混合模型预测控制
混合逻辑动态 模型 (mixed logical dynamical,MLD)主要用于混合系统的建模和控制,其模型可以用线性动态方程组和线性约束不等式组来描述。ACC 系统的混合模型预测控制设计思想:在给定限制条件下建立预测模型,然后构造相应的约束优化,采用MLD 将MPC 的优化问题转换成混合整数线性规划问题,实现混合模型预测控制的滚动优化过程。
1.1 预测模型
混合模型预测控制采取的MLD 模型为

式中:x (k)——第k 个采样时刻系统的状态向量,包括车辆当 前 位 置 和 当 前 速 度,即x (k)= [s,v]。u(k)——系统控制输入向量,δ (k)和z (k)——辅助变量,其中δ (k)∈ {0,1},z (k)∈R。A 和Bi——实数常量矩阵。
基于巡航车的安全、舒适考虑,需要给系统一些限制,因此在巡航车的位置、速度和加速度上增加如下限制

式中:x (1,k)和rx (1,k)——表示巡航车和前车的位置,dsafe——前车 与 巡 航 车 之 间 的 安 全 距 离,x (2,k)——表示巡航车的速度,它的范围为 [13m/s,34m/s],并且amin=-2m/s和amax=2.5m/s,Ts为采样间隔。
1.2 滚动优化
滚动优化控制是模型预测控制的主要特征,通过在滚动优化域中计算一个最小化的无限域优化控制问题来确定预测序列。
代价函数为如下形式

式中:Np——优化控制域,x (k+j|k)和u (k+j|k)——k采样时刻预测的k+j 时刻的系统状态和控制输入。rx (k+j)——k+j采样时刻前车的状态。QNp、R 和Qx——权值,可以离线计算。
由代价函数产生的预测序列分别为控制输入向量U(k)、辅助向量ε (k)和Z (k)

控制序列中每个向量的第一个元素u (k)、δ (k)和z(k)作为MLD 模型式 (1)的输入,求得x (k+1)的值。控制序列中其他元素被丢弃,x (k+1)作为初始状态更新优化问题式 (3)。
HYSDEL自动将代价函数转换为线性向量;位置、速度和加速度的限制及前车状态转换成不等式组。将模型预测控制转化为在线求解混合整数线性规划问题。即

式中:f——代价函数的线性向量,xm——Np 个控制输入和辅助向量的序列,g——限制不等式集。
2 改进的粒子群算法
粒子群优化算法的基本思想是:系统初始化一组随机的合法解,粒子群中的每个粒子通过跟踪自身的个体最优解和整个粒子群的全局最优解来不断的更新每次迭代的位置和速度。当得到允许误差范围内的最优解或达到最大迭代次数时,粒子群优化算法终止。
结合多目标优化的PSO 算法的主要思想是:将混合整数线性规划问题转换为具有两个目标的多目标优化问题,第一个目标为原问题的目标函数f (x),第二个目标为粒子违反约束条件的程度G (x)[12]。然后根据Pareto支配原则挑选最优解。
2.1 算法中的基本概念
(1)违反约束程度
第i个解pi违反第j 个约束的程度可表示为

其中,i= {1,2,…,N},j= {1,2,…,q}。N 为粒子群的规模,q为约束不等式的个数。
解pi违反约束的程度记为
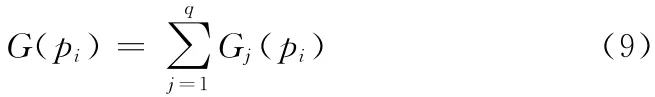
其中,如果G (pi)值为0,则表示pi为可行解,否则pi为不可行解。
(2)Pareto支配
如果解pi的Pareto支配解为pk,那么满足

其中,l= {1,2,…,q}。解pi的Pareto支配解为pk记为pi<pk。
(3)被支配度
种群中所有支配解pi的个体组成的集合为Pareto支配集PDS
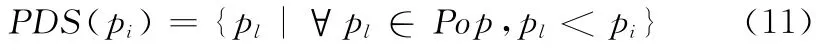
其中,Pop 为所有解的集合,PDS (pi)集合中元素个数为解pi的被支配度。
2.2 算法中的操作
(1)速度更新

其中,k= {1,2,…,max_gen},max_gen 为最大迭代次数,d= {1,2,…,D},D 为解的维数,c1和c2为学习因子,分别表征了粒子思考自身和学习群体中其他粒子的能力。c1、c2在此实验中都设置为固定值2,r1d和r2d为随机值,ω 为惯性权重,它的范围是 [0.4,0.9],随着迭代次数的增加,ω 递减。计算式为

其中,ωmax=0.9,ωmin=0.4。
(2)位置更新

其中,k= {1,2,…,max_gen},d= {1,2,…,D}。
(3)个体最优解更新
(4)全局最优解更新
检查所有粒子的个体最优解,看个体最优解中是否有可行解:①若有可行解,则从可行解集中找出具有最小适应值的个体最优解来更新整个粒子群的最优解;②若没有可行解,则计算粒子群中每个个体最优解的被支配度,所有被支配度为0的粒子构成Np 的非劣集F,比较非劣集F中所有个体的违反约束程度,用具有最小违反约束程度的个体最优解来更新整个粒子群的最优解。
2.3 改进的粒子群算法
改进的粒子群算法的具体流程如下:
步骤1 采用随机选取方式,初始化粒子群中每个粒子的速度和位置;
步骤2 使用粒子的位置信息进行初始化,求解粒子群个体的最优解;
步骤3 根据每个粒子的个体最优解初始化粒子群的全局最优解;重复步骤4至步骤6,直到获得满足要求的最优解或达到最大迭代次数;
步骤4 更新粒子的位置和速度;
步骤5 根据每个粒子的当前位置和上一次迭代的个体最优值更新当前迭代的个体最优解;
步骤6 从N 个粒子的个体最优解中选择最优值更新粒子群全局最优解;
步骤7 返回找到的全局最优解。
3 改进的粒子群优化的混合模型预测控制
将改进的粒子群优化算法应用到混合模型预测控制中,具体算法流程如下:
步骤1 建立式 (1)的MLD 模型,作为算法的预测模型;
步骤2 为模型添加限制,建立模型的混合控制器;
步骤3 开始仿真控制器的控制过程,令k=1;
步骤4 在k采样时刻,采样获得前车的状态,并根据此状态更新系统的代价函数式 (3)和约束不等式 (7)。
步骤5 利用MPSO 计算MILP 问题,得到新的预测序列U (k)、ε (k)和Z (k);
步骤6 第一个控制输入u (k)、δ (k)和z (k)用来执行车辆控制,并且根据MLD 模型更新x (k+1);
步骤7 令k=k+1,重新从步骤4 开始,直到结束采样。
4 仿真结果
仿真实验分别列出使用GLPK 和MPSO 算法求解MILP的混合模型预测控制巡航车得到的仿真结果,并对两种混合模型预测控制框架得到的结果进行比较。仿真工具采用MATLAB 7.8,编程工具采用Visual studio 2010,操作 系 统 是windows XP SP3,处 理 器 是AMD Athlon(2.81GHz)。
仿真环境是高速公路下的自适应巡航控制。前车的初始速度为60km/h,巡航车辆初始速度为55km/h,与前车的初始距离为20m。
图1显示了仿真过程中前车的基于GLPK 的HMPC 和基于MPSO 算法的HMPC控制的巡航车速度变化情况。可以看出两种HMPC 框架的巡航车都能很好地跟踪前车的速度。

图1 仿真过程巡航车跟踪前车的速度变化
图2显示了仿真过程巡航车的加速度变化。从结果可以看出两种HMPC框架产生的加速度都满足约束条件。
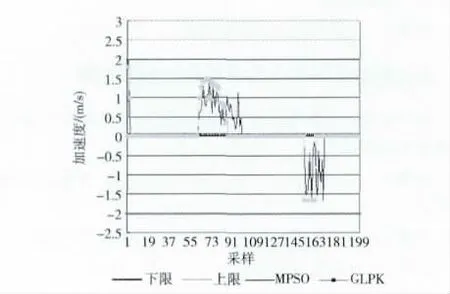
图2 仿真过程巡航车的加速度变化
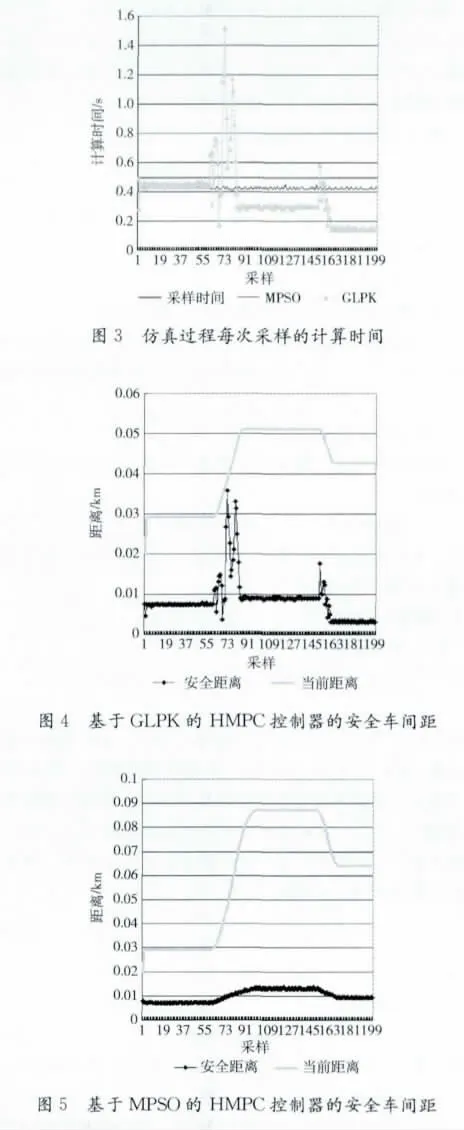
图3显示了仿真过程每次采样的计算时间。采样周期是0.5s。使用基于GLPK 的混合模型预测控制的采样计算时间超过了采样间隔,不能满足汽车ACC 的实时要求。而基于MPSO 的混合模型预测控制的采样计算时间都小于0.5s,符合采样的时间要求。
由于巡航车的速度和每次采样的计算时间不同,所以安全车间距也在不断变化。仿真过程中,基于GLPK 的HMPC控制器和基于MPSO 的HMPC 控制器的安全车间距和两车的实时车间距变化情况如图4 和图5,两种HMPC框架得到的车间距都大于两车的安全距离。
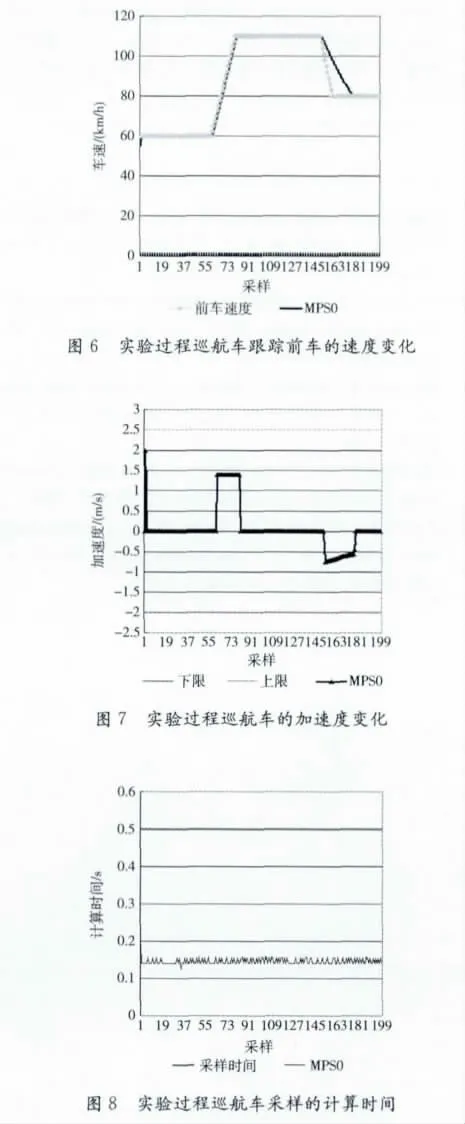
在车辆上实现ACC系统时,使用C语言编程,为更准确考察实现的程序在车辆上运行能否满足要求,在Visual studio 2010上实现了MPSO 的优化过程,实验结果如图6-图9。结果显示各方面的性能都优于Matlab 7.8 上取得的结果,尤其是每次采样的计算时间变得更短。
5 结束语
利用混合模型预测控制方法实现了车辆的自适应巡航控制。提出的MPSO 算法结合了多目标优化技术和标准PSO 算法,适用于求解混合优化问题。为了加速混合模型预测控制的过程,提出在模型预测控制的滚动优化阶段采用MPSO 算法求解混合整数线性规划问题。Matlab和VC仿真实验结果表明,提出的自适应巡航控制方法能够使巡航车辆很好地跟踪前导车辆,并且MPSO 能够加速混合模型预测控制,明显改进ACC系统的车辆跟踪问题。

图9 实验过程巡航车与前车的安全车间距
下一步将会在分布式系统上实现基于改进的粒子群优化算法的混合模型预测控制,利用多个电子控制单元 (e-lectronic control unit,ECU)的资源进一步加速控制过程,实现更好的车辆主动安全的性能。
[1]Rajamani R.Vehicle dynamics and control [M].Springer Science,2012:141-170.
[2]Zheng T.Model predictive control [M].Rijeka,Croatia:Ciyo,2010:1-110.
[3]Kouro S,Cortes P,Vargas R,et al.Model predictive control--a simple and powerful method to control power converters [J].IEEE Trans Industrial Electronics,2009,56 (6):1826-1838.
[4]Mariethoz S,Domahidi A,Morari M.High-bandwidth explicit model predictive control of electrical drives[J].IEEE Trans Industry Applications,2012,48 (6):1980-1992.
[5]Wang Y,Boyd S.Fast model predictive control using online optimization [J].IEEE Trans Control Systems Technology,2010,18 (2):267-278.
[6]Vratislav H,Lubos P,Jan S.Modeling of a system with hybrid dynamics [J].Acta Electrotechnica et Informatica,2011,11 (1):14-19.
[7]Michal K,Dawid Z,Iwona P K.Overlay multicast optimization:IBM ILOG CPLEX [J].International Journal of Electronics and Telecommunications,2013,58 (4):381-388.
[8]Susuki R,Kawai F,Nakazawa C,et al.Parameter optimization of model predictive control using PSO [C]//Proc SICE,2008:1981-1988.
[9]Na D,Zengqiang C,Qinglin S,et al.Particle-swarm optimization algorithm for model predictive control with constraints[J].Control Theory &Applications,2009,26 (9):965-969.
[10]Pradipto G,Bruce A C.Numerical trajectory optimization with swarm intelligence and dynamic assignment of solution structure[J].Journal of Guidance,Control,and Dynamics,2012,35 (4):1178-1191.
[11]HE Yijun,CHEN Dezhao.Hybrid particle swarm optimization algorithm for mixed-integer nonlinear programming [J].Journal of Zhejiang University,2008,42 (5):747-751 (in Chinese).[贺益君,陈德钊.适于混合整数非线性规划的混合粒子群优化算法 [J].浙江大学学报,2008,42 (5):747-751.]
[12]WANG Yong,CAI Zixing,Zhou Yuren,et al.Constrained optimization evolutionary algorithms [J].Journal of Software,2009,20 (1):11-29 (in Chinese).[王勇,蔡自兴,周育人,等.约束优化进化算法 [J].软件学报,2009,20(1):11-29.]
