基于MapReduce模型的并行遗传k－means聚类算法

贾瑞玉，管玉勇，李亚龙

（安徽大学 计算机科学与技术学院，安徽 合肥230601）

0 引 言

K－means算法是聚类算法中划分聚类的一种，由于算法简单且高效，因此得到了普遍的应用。但是k－means算法的聚类结果的准确性不是很高，计算量较大，对初始化中心较为敏感［1］。目前有许多针对k－means算法的研究，文献［2］主要针对k－means算法对初始聚类中心敏感提出基于密度的改进算法。文献［3］提出了自动获取最佳k值的算法。文献［4］将并行的遗传算法和k－means算法相结合，优化聚类的结果和k值。文献［5］将k－means算法放在Hadoop平台下进行并行化设计可以提高算法运行的时间效率以及改善最后的聚类结果。将遗传算法加入到k－means算法中去可以明显的改善k－means算法的性能［6］，但是串行的算法会增加程序运行的时间。因此，有必要对其进行并行化设计。

传统的基于MPI或PVM 的并行化设计，不仅需要对计算机的体系结构有较好地认识，实现起来也比较困难，而且节点之间的通信开销会占据较多的时间［7］。相对于此，MapReduce并行化模型不需要编程人员去考虑体系结构方面的细节知识，实现起来较为容易，而且节点之间的通行时间也会减少。因此，目前基于MapReduce模型的并行化设计是当前的研究热点之一，文献 ［8－10］分别从不同方面研究了遗传算法的MapReduce并行化设计，但主要都是基于遗传算法粗粒度并行化模型进行设计。将遗传k－means算法进行并行化设计不仅可以提高算法执行的时间效率，在一定程度上还可以防止早熟现象的发生，从而提高聚类的效果。

1 遗传k－means聚类算法

k－means聚类算法虽然简单、通用，但是对初始聚类中心的选择较为敏感，所以需要对初始聚类中心的选择进行优化。遗传算法是一种智能搜索算法，它不依赖于问题的本身，所需要的仅是通过事先设定的适应度函数，对算法产生的染色体进行评价，使适应度高的染色体得到更好的繁殖机会。算法的终止条件是事先设定的最大遗传代数或者是达到最佳适应度值。将遗传算法加入到k－means算法中去，利用遗传算法的优势可以较好地克服k－means算法的一些不足。

遗传k－means聚类算法具体的做法是：将各个聚类中心坐标作为染色体的基因，染色体的长度等于聚类中心的个数；然后初始化若干个相异的染色体作为一个种群进行遗传操作；最后得到适应度最大的染色体，解析出各个中心点的坐标即可以认为是最佳的聚类中心坐标。算法的主要步骤如下：

（1）初始化运行参数 （种群个数p，聚类个数k，最大遗传代数）。

（2）初始化种群即随机产生p个染色体，每个染色体表示一个聚类的结果。

（3）对每个染色体进行k－means操作，然后评价其适应度并记录。

（4）判断是否达到结束条件 （满足最大代数或问题最优解），未满足则进行以下操作：

1）选择操作

2）交叉操作

3）变异操作

（5）转到步骤 （3）。

1.1 适应度函数设计

遗传聚类算法中的每一个染色体表示一个聚类的结果，而判断一个聚类结果的好坏标准是要求各个划分集合之间的联系要松散而集合内的各个数据对象间的联系要紧密。所以适应度函数设计为

其中，分子表示一个染色体中各个聚类中心之间的最大距离；分母表示各个集合中的数据点到其中心点的距离总和。

1.2 遗传算子

选择算子：为保护最优个体可以代代相传，采用无条件保留种群中的最优个体复制到下一代，用来替换新种群中的最差个体。同时对于种群中的其它个体采用概率选择的方法复制到下一代：适应度较大的个体有较大的机会复制到下一代中。

选择概率

其中，分子表示个体的适应度值，分母表示种群中所有个体的适应度值之和。

交叉算子：对种群中的n 个个体随机选择两两配对，进行交叉操作。本文采用基于最短基因距离的单点交叉策略。

变异算子：种群中的个体变异可以维护种群的多样性，也可在一定程度上防止种群的早熟现象的发生。变异的概率一般较低，一般在0.001～0.01之间。

2 遗传k－means聚类算法的并行化实现

遗传k－means算法虽然提高了聚类效果的准确性，但同时也产生了效率低的问题，尤其是在处理大数据集时，这样的问题显得尤为突出。考虑到遗传算法具有的天然并行性，可以将遗传聚类算法进行并行化设计。这样不仅提高算法的时间效率而且增加了种群的多样性，可以防止早熟现象的发生。

2.1 MapReduce模型

Hadoop平台下的MapReduce 并行计算模型是模仿Google开发出的MapReduce 并行计算模型，而且是开源免费的。

MapReduce模型首先对输入的数据有格式的要求，必须以键值对＜key，value＞的形式作为输入，key可以理解为数据的编号，value表示数据的值。其次数据的处理过程主要分为Map过程和Reduce过程。Map过程主要对原始的输入数据进行处理产生中间的＜key'，value'＞，然后根据相同的key'，对数据进行规约处理，作为Reduce过程的输入，最后输出结果。它的计算模型如图1所示。

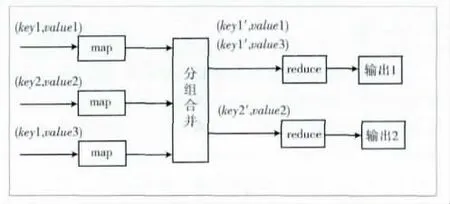
图1 MapReduce简单计算模型

2.2 种群迁移策略

种群迁移作为遗传算法的并行化设计是区别于串行遗传算法的重要方面，常用的方法是最优／最差替换法，即将子种群中的最优个体迁出用来替换邻居种群中的最差个体。在每一个Map过程中，改变满足条件的染色体的编号从而达到迁移的目的。

2.3 Map和Reduce过程设计

针对MapReduce模型对输入数据的特殊性要求，将本文的输入数据格式化为＜key，value＞的形式，其中key表示子种群的编号，value表示个体的值。此外，将染色体的长度设为k＋1，最后一位用于存储个体的适应度值，初始化时设为0。个体的初始化、适应度评价和k－means操作可以放在Map过程进行；Reduce过程主要是针对相同的键，达到停机条件，输出各个子种群中最优的个体，然后再选出这些最优个体中的最优个体，根据每个染色体最后一位的适应度值。否则，完成一个子种群的遗传操作。

3 实 验

采用4台普通的计算机搭建的Hadoop集群系统进行实验，Hadoop的版本是Hadoop－0.20.2。每台计算机使用的操作系统是Red Hat Linux 9.0版本。所使用的数据集是人工数据，维度为2。分别构造了3个数据集Data1，Data2，Data3。Data1 包 含100 个 数 据，分 为3 类；Data2 包 含1000个数据，数据类别5；Data3包含了5000个数据，类别为10。各数据集每个类别中包含的数据个数都是相等的。采用运行20次的平均值作为最终的实验结果。相关的参数设置：交叉概率为0.9；变异概率为0.009；种群大小设为40；算法的最大迭代次数设为50。

由表1可以看出k－means算法即使在处理小的数据集时所得到的结果往往也不太理想，再将遗传算法加入到kmeans算法中，所得到的相应的结果明显得到了改善。然后再将其进行并行化设计后，随着处理的数据集规模不断增大，所得到的聚类结果和串行的算法相比较也会有明显的改善。这主要是因为并行遗传算法能够有效防止早熟现象的发生从而收敛到较好的结果。

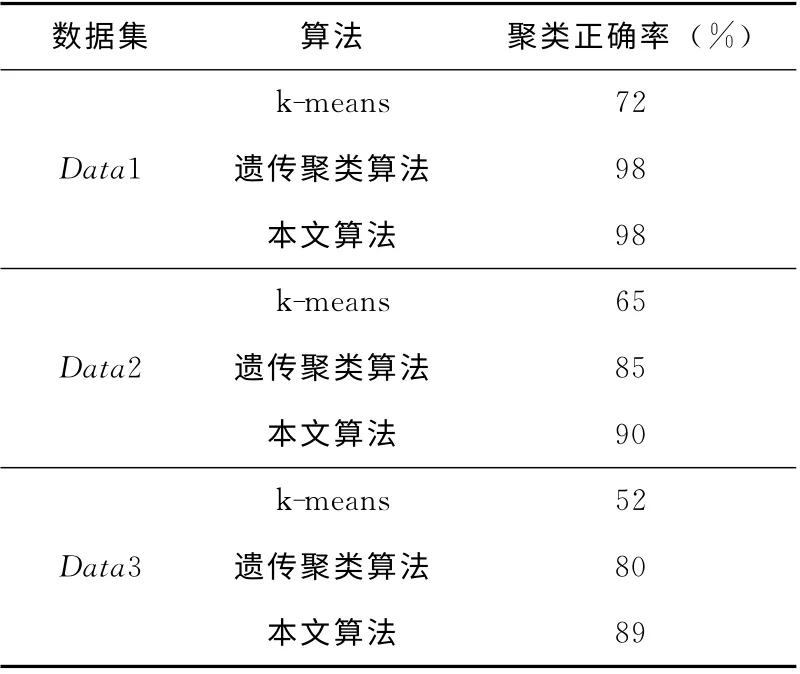
表1 不同算法的聚类性能比较

图2反映了加速比与节点数之间的关系，从图2可以看出，加速比与节点数并不是线性关系或正比例关系，这主要是因为随着节点数的增加，节点之间的通信开销也会增大，但对于在相同的节点数下面，数据集规模越大，所得到的加速比也会较大。而且对于大数据集，随节点数增加，加速比增加的更快一些。这是因为大的数据集可以更有效地利用每个节点的计算性能。

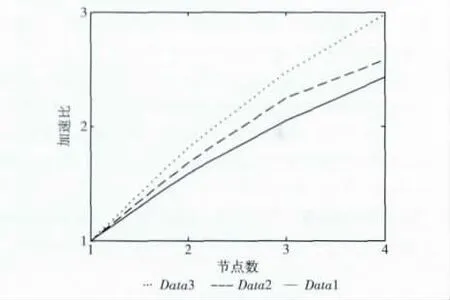
图2 节点数与加速比的关系

图3主要反映了算法的并行效率，从图3中可以看出，数据规模较小的并行效率要低于数据集较大的并行效率，而且随着节点数的增加，下降会更快一些；而数据规模较大时，下降得更为平缓。这些主要是因为数据规模增大，处理的时间也会增加，节点数的增加，节点之间的通信开销也会增加。从图2 和图3 可以得出并行化后的遗传kmeans算法具有良好的并行性和可扩展性。

4 结束语

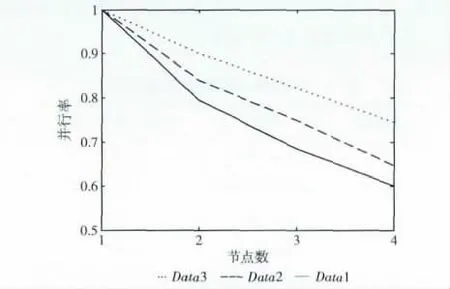
图3 节点数与并行效率的测试结果

将智能算法与聚类算法相结合可以提高聚类算法的聚类结果，但同时又会产生智能算法的低时间效率的问题。遗传k－means算法在Hadoop平台下的并行化设计和实现，不仅提高了算法运行的时间效率而且也改善了算法运行的结果。

对于如何改进遗传算子加速收敛从而缩短达到最优的遗传迭代次数，以及对k－means算法中如何确定最佳的k值，能否通过可变长的染色体来达到，这些都是有待于以后进行研究的问题。

［1］LI Qun，YUAN Jinsheng.Optimal density text clustering algorithm based on DBSCAN ［J］.Computer Engineering and Design，2012，33 （4）：1409－1413 （in Chinese）. ［李群，袁金生.基于DBSCAN 的最优密度文本聚类方法 ［J］.计算机工程与设计，2012，33 （4）：1409－1413.］

［2］LAI Yuxia，LIU Jianping.Optimal study on initial center of kmeans algorithm ［J］.Computer Engineering and Applications，2008，44 （10）：147－149.（in Chinese）［赖玉霞，刘建平.kmeans算法的初始聚类中心的优化 ［J］.计算机工程与应用，2008，44 （10）：147－149.］

［3］TIAN Senping，WU Wenliang.Algorithm of automatic gained parameter value k based on dynamic k－means［J］.Computer Engineering and Design，2011，32 （1）：274－276 （in Chinese）.［田森平，吴文亮.自动获取k－means聚类参数k值的方法 ［J］.计算机工程与设计，2011，32 （1）：274－276.］

［4］DAI Wenhua，JIAO Cuizhen，HE Tingting.Research of kmeans clustering method based on parallel genetic algorithm［J］.Computer Science，2008，35 （6）：171－174 （in Chinese）.［戴文华，焦翠珍，何婷婷.基于并行遗传算法的kmeans聚类研究 ［J］.计算机科学，2008，35 （6）：171－174.］

［5］ZHAO Weizhong，MA Huifang，FU Yanxiang，et al.Research on parallel k－means algorithm design based on Hadoop platform ［J］.Computer Science，2011，33 （10）：166－168（in Chinese）.［赵卫中，马慧芳，傅燕翔，等.基于云计算平台Hadoop的并行k－means聚类算法设计研究 ［J］.计算机科学，2011，33 （10）：166－168.］

［6］LU Linhua，Wang Bo.Improved genetic algorithm－based clustering approach ［J］.Computer Engineering and Application，2007，43 （21）：170－172 （in Chinese）.［陆林华，王波.一种改进的遗传聚类算法 ［J］.计算机工程与应用，2007，43（21）：170－172.］

［7］ZHAO Jiuling，WEI Haipeng.Design and realization of parallel genetic algorithm based on MPI ［J］.Computer Science，2006，33 （9）：186－189 （in Chinese）. ［赵玖玲，卫海鹏.基于MPI的并行遗传算法的设计与实现 ［J］.计算机科学，2006，33 （9）：186－189.］

［8］Verma A，Llora X，Goldberg D E，et al.Scaling genetic algorithms using mapreduce ［C］／／In International Conference on Intelligent Systems Design and Applications，2009.

［9］Jin C，Vecchiola C，Buyya R.Mrpga：An extension of mapreduce for parallelizing genetic algorithms［C］／／IEEE Fourth International Conference on eScience，2008：214－221.

［10］LI Dong，PAN Zhisong.Research on parallel genetic algorithm based on MapReduce ［J］.Computer Science，2012，39 （7）：182－204 （in Chinese）. ［李东，潘志松.一种适用于大规模变量的并行遗传算法研究 ［J］.计算机科学，2012，39 （7）：182－204.］