量子原胞自动机遗传模拟退火算法改进研究

周日贵，肖天儒

（华东交通大学 信息工程学院，江西 南昌330013）

0 引 言

量子原胞自动机作为新型纳米器件首先由C.Lent等人提出，与传统CMOS器件相比，它具有器件超高密度、极低功耗、克服线路共面穿越信号相互干扰等独特的优点，因此受到人们广泛的关注和研究。近些年来，人们对量子原胞自动机的仿真研究进展显著［1－3］，主要焦点在于如何提高仿真的速度以及仿真的精准度。由于纳米元件工作时是否稳定极受温度的影响，因此有学者提出用模拟退火的方法［4］对量子电路进行仿真，此方法是把量子细胞半经典化，将细胞中的电子看作是经典力学中的粒子来进行模拟退火的，这种方式由于增加了对当前最优解的记忆功能，因此对于少数量子细胞信号传递的模拟此方法就存在着高复杂度的计算问题，另外，其仿真结果正确率也较低，虽然Macucci等人也提到循环退火可以提高仿真的正确率，但对于高复杂度的量子电路［5］而言，利用这种方法依然会使系统陷入仿真时间过长的局面。遗传算法与模拟退火算法的结合对于寻找全局最优解具有一定实效性［6］，将其用于量子原胞自动机仿真，可以缩短仿真时间，且在一定程度上提高了量子电路系统的收敛的速率，然而随着电路规模的扩大仿真的正确率就会明显下降。赵晓辉等人将量子遗传算法应用于量子原胞自动机仿真［7］，当仿真过程中出现多极值问题时，此方法有效降低了陷入局部最优的概率，在一定程度上解决了仿真正确率不高的问题。通过比较分析上述仿真方法，它们存在共同的弊端，即在处理大规模量子电路时，仿真时间过长，仿真精确度不高。

本文针对量子原胞自动机遗传模拟退火算法应用于较大型QCA 电路效率不高、准确度较低的问题提出了新的解决方法，它主要通过对QCA 电路中的可定态细胞定态来减小遗传模拟退火处理问题的规模，被减小的规模部分可利用定态规则来计算电路的状态，这样就可使得仿真速度更快，仿真结果更精确。

1 量子原胞自动机概述

1.1 量子细胞

量子原胞自动机电路的最小单元是量子细胞，量子细胞由4个量子点和两个自由电子构成，由于库仑作用力的排斥作用，两个自由电子更易处于对角线上的两个量子点上［8］。如图1所示，空心圆圈表示量子点，实心圆表示电子，电子位于左对角线上时，细胞的极化状态为＋1，位于右对角线上时，极化状态为－1。

图1 量子细胞

1.2 相互作用能

量子原胞电路中的细胞负载的信号在电路系统处于稳定态时应是让系统的静电能处于最小的信号。量子电路系统总静电能量的计算式［9］见式 （1）

其中，qi表示第i个量子点的电荷量，ε0与ε1分别是真空介电常数和介质相对介电常数，rij表示量子点i与j 的距离。

2 定态规则与可定态细胞

2.1 3×3QCA子系统

王森等人提出了3×3QCA 细胞模块化设计的方法［10］，3×3QCA 子系统如图2所示。

2.2 定态规则证明

假设QCA 细胞被锁存时极化率只存在p ＝－1 和p＝＋1两种状态，QCA 细胞参数按文献 ［7］进行设置，细胞尺寸s＝20nm×20nm ，细胞最小间距d＝20nm ，细胞内相邻量子点间距a ＝10nm ，细胞有效影响半径为r ＝41nm 。

图2 QCA 模块子系统

文献［10］中提到相邻两个细胞组合共有5种配置能量ei（1≤i≤5），如图3所示。配置能量的计算可利用式（2）

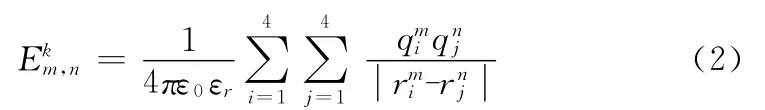
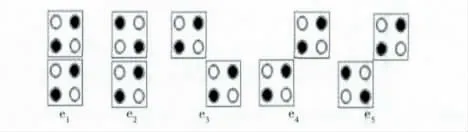
图3 相邻细胞不同配置

接下来，我们通过比较分析5种配置能量来确定细胞极化状态判定的规则，此规则可以描述为

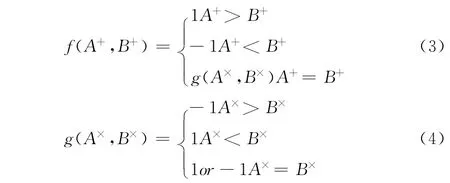
式中：f、g——可定态细胞 （位置5 细胞）的极化状态，A＋（B＋）——2、4、6、8位置极化状态为＋1 （－1）的个数，A×（B×）——1、3、7、9 位置极化状态为＋1 （－1）的个数。

下面是规则的证明过程，利用式 （2）计算5种配置能量，结果见表1。

表1 不同细胞间距的配置能量

由表1可知e1＝－e2，e3＝e4＝－e5。假设要求极化状态的细胞位置位于3×3QCA 子系统位置5 （如图2所示）。其它位置放置极化状态已定的细胞或不放细胞，如果系统中有i个e1，j个e2，m 个e3，n个e4，p 个e5，则子系统总能量为

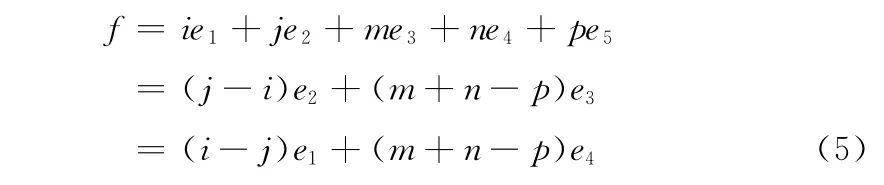
步骤1 证明位置2、4、6、8的细胞对位置5细胞的影响力权值要大于1、3、7、9位置的细胞。

ie1＋je2刻画了2、4、6、8位置细胞与位置5细胞的能量关系，因为e1＝－e2，若2、4、6、8位置上有多个细胞，能量会相互抵消，所以只考虑只存在一个细胞的情况，此时系统能量有式 （6）、式 （7）两种可能

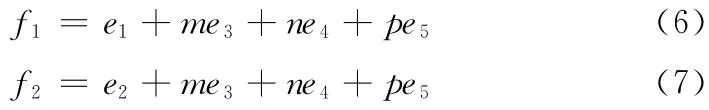
对于式 （6），因为e1＜0，要体现2、4、6、8的细胞对位置5细胞的影响力更大，则要使1、3、7、9位置的细胞与位置5的细胞能量和尽可能的大，于是有

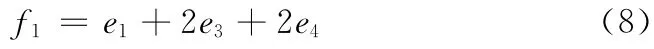
因为f1＜0，即1、3、7、9位置的细胞与位置5细胞能量总和最大时，子系统的能量也为负，说明2、4、6、8的细胞对位置5 细胞的影响力要大于1、3、7、9 位置的细胞。

对于式 （7），因为e2＞0，要体现2、4、6、8的细胞对位置5细胞的影响力更大，则要使1、3、7、9位置的细胞与位置5的细胞能量和尽可能的小，于是有

因为f2＞0，即1、3、7、9位置的细胞与位置5细胞能量总和最小时，子系统的能量也为正，说明2、4、6、8的细胞对位置5 细胞的影响力要大于1、3、7、9 位置的细胞。

步骤2 证明2、4、6、8位置不放细胞或放了细胞能量相抵消，e3、e4个数大于e5个数的系统能量更大，否则更小。

如果2、4、6、8位置不放细胞或放了细胞能量相抵消，则系统能量为

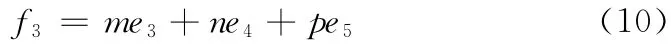
由e3＝e4＝－e5易证e3、e4个数大于e5个数的系统能量更大，否则更小。

2.3 可定态细胞

设位置5的细胞为要求极化状态的细胞，那么其邻域每个位置有4种情形：极化状态为＋1的细胞、极化状态为－1的细胞、未知极化状态的细胞、没有细胞。不防设3×3QCA 子系统位置5细胞邻域所有环境为集合A，可定态细胞环境为集合P，不可定态细胞环境为集合U 。设位置2、4、6、8细胞极化状态为＋1的细胞个数为p1，极化状态为－1的细胞个数为n1，极化状态未知个数为x1，位置1、3、7、9细胞极化状态＋1的细胞个数为p2，极化状态为－1的细胞个数为n2，极化状态未知个数为x2。则不可定态细胞环境可表示为

由于当x1，x2大于等于极化状态已定的细胞个数时，即位置5细胞邻域大部分位置细胞状态不定，所以其极化状态暂时无法判断。

知U 可推出可定态细胞环境集合为P ＝A ∩U ，定义满足环境P 的细胞为可定态细胞。

3 遗传模拟退火算法 （gass）

3.1 编码方法、适应度函数与退温函数

假设细胞存在两种极化状态，故编码方法可用二进制编码。把QCA 电路作为一条染色体，电路中的细胞作为基因。

退温函数采用线性函数，tk＋1＝αtk，其中α小于并极接近于1，本文设α＝0.95。

3.2 选择、交叉和变异过程

选择是根据适应函数的概率分布由高到低优先选出概率值最高的新种群的过程，交叉时采用变化交配法，由于是二进制编码，因此基因变异的概率较小，可设基因变异概率为Pm＝0.001。

3.3 中止规则

最大遗传代数设为MAXGEN ，当迭代次数达到最大遗传代数MAXGEN 时算法中止。

3.4 算法伪代码描述

proc gsaa；

var g，MAXGEN，Maxpop，ej，ei，r；

‘变量定义，g表示迭代次数，MAXGEN 表示最大遗传代数，Maxpop表示最大种群数目，ej表示新染色体的能量，ei表示旧染色体能量

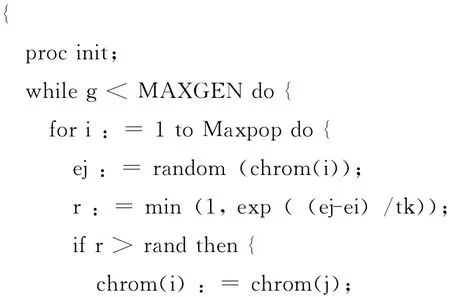
4 改进的遗传模拟退火算法 （lgass）

4.1 可定态细胞的判定

根据式 （11）通过寻找细胞邻域环境已知和未知极化状态的细胞的个数来判断细胞是否为可定态细胞。

4.2 可定态细胞极化率计算

根据定态规则对可定态细胞极化状态进行计算。

4.3 改进算法伪码描述

4.3.1 结构体变量定义

4.3.2 函数的定义

func divByClk（circuit：cell），此函数的作用是将整个电路按时钟域划分成4个量子阵列。

func checkPolar（ccell：cell）：boolean，此函数用于判断某个量子细胞是否可定态。

func calPolar（ccell：cell），此函数用来计算量子细胞的极化状态。

func setup（ccell：cell，ncell：cell），此函数根据电路环境对某个量子细胞邻域环境进行设置。

func updateCircuit（），此函数用于更新电路状态，当某个细胞的状态发生改变时就立即更新电路状态。

func make（cirClk：cell，circuit：cell），此函数按时钟域依次确定细胞极化状态。

4.3.3 make函数伪码

鉴于divByClk，checkPolar，calPolar，setup，update－Circuit函数代码易于实现，在此只对make 函数作伪码描述。

5 仿真实验与结果分析

在进行仿真实验时，对量子细胞参数设置如下：细胞尺寸s＝20nm×20nm ，细胞最小间距d＝20nm ，细胞内相邻量子点间距a＝10nm ，细胞有效影响半径为r＝41nm。仿真实验环境：Windows操作系统，Matlab工具软件。

5.1 仿真实验一

为检验算法的有效性，我们先对基本的逻辑电路进行仿真，4种基本逻辑电路的设计如图4所示。将gsaa与lgsaa分别应用于基本电路仿真，为方便对比，假设用lgsaa算法处理的电路系统初始为能量最大状态，这样两种算法对比得到图5仿真结果。

限于文章篇幅，输入细胞其它输入信号情况在此不作详细描述，其它输入信号也同样可得到正确的仿真结果。gass算法与lgass算法对4种基本的逻辑电路仿真的正确率见表2。

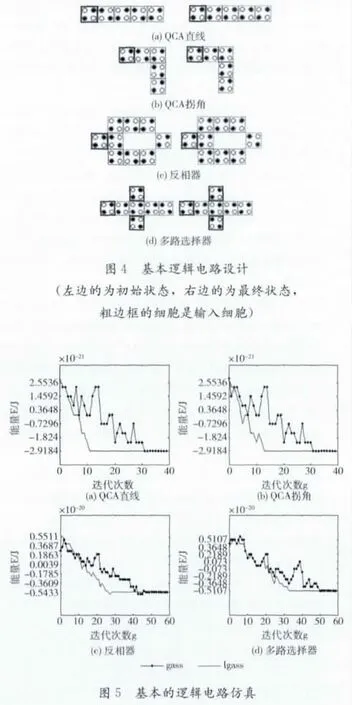
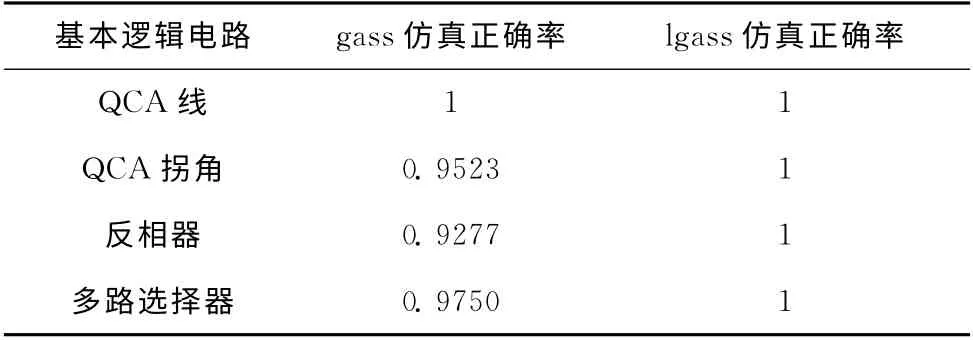
表2 基本逻辑电路gass与lgass仿真正确率比较

5.2 仿真实验二

为检验算法的优越性，我们将gsaa与lgsaa分别应用于一较大规模电路 （如图6所示）。图7展示了此电路系统收敛过程两种算法迭代次数。lgass算法在迭代次数到达100至150之间时，电路系统将处于能量最低状态，而gass算法电路系统能量还处于较高的不稳定状态。

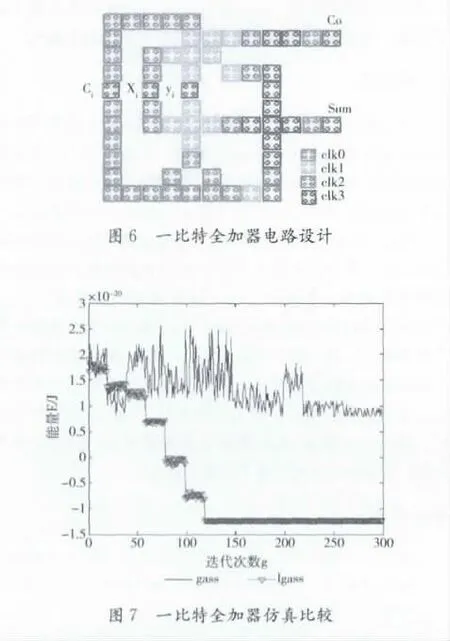
接下来，我们比较两种算法应用于大型电路的仿真正确率，利用gass算法与lgass算法对图6电路进行100次仿真，每次得到的仿真结果由QCADesigner来检验，若得到的结果与QCADesigner仿真得到的结果一致，则认为仿真正确，否则认为仿真不正确。通过对比，两种算法仿真正确率和最大误差值见表3。

表3 gass与lgass仿真正确率比较

5.3 结果分析

由图5和图7可以看出，lgass算法相比于gass算法能在较少迭代次数的情况下达到电路系统能量较低的效果，并且lgass算法曲线波动性明显小于gass曲线，从而可以判断lgass算法比gass算法收敛速度更快。这就克服了实际应用中系统仿真长时间等待的弊端。

由表2与表3可知，lgass算法在提高仿真速度的同时也大大提高了仿真的精准度，对于一些基本的逻辑电路两种算法都可在较短时间内得到正确率高的仿真结果，其中lgass算法仿真正确率近乎为1。对于大规模量子电路而言，在同样的仿真时间内，gass算法的应用会使仿真正确率明显下降，而lgass算法却依然保持了较高的仿真正确率。

6 结束语

本文做的主要工作是首先提出了3×3QCA 模块子系统判断极化状态的规则，即定态规则，并且证明了定态规则的正确性，根据规则定义了可定态细胞，然后设计了基于定态规则的局部遗传模拟退火算法 （lgass）并将其应用于大型QCA 电路仿真。算法中对可定态细胞的先定态操作的目的是为了减小模拟退火算法问题的处理规模从而提高电路的仿真效率。从理论上讲，遗传模拟退火算法 （gass）对大型QCA 电路仿真是可行的，如果算法参数如遗传代数设置足够大，退火循环次数足够大，那么QCA 电路仿真的正确率就会无限接近于1，然而这在实际应用当中不大可能。文章最后利用两个仿真实验验证了lgass算法的有效性，相比gass算法lgass算法收敛速度更快，仿真正确率更高，更有利于大规模量子电路的仿真。

［1］Jarosaw Adam Miszczak.High－level structures for quantum computing ［J］.Synthesis Lectures on Quantum Computing，2012，4 （1）：1－129.

［2］Miszczak J A.Models of quantum computation and quantum programming languages［J］.Bulletin of the Polish Academy of Sciences：Technical Sciences，2011，59 （3）：305－324.

［3］Ganesh E N，Kishore L.Implementation of quantum cellular automata combinational and sequential circuits using majority logic reduction method ［J］.International Journal of Nanotechnology and Applications，2008，2 （1）：89－106.

［4］ZHU Haodong，ZHONG Yong.A kind of renewed simulated annealing algorithm ［J］.Computer Technology and Development，2009，19 （6）：32－35 （in Chinese）. ［朱颢东，钟勇.一种改进的模拟退火算法 ［J］.计算机技术与发展，2009，19（6）：32－35.］

［5］Bibhash Sen，Manojit Dutta.An efficient multiplexer in quantum－dot cellular automata［G］.LNCS 7373：Progress in VLSI Design and Test，2012：350－351.

［6］XUE Yingchun，XU Wenbo，SUN Jun.Rectangle－packing optimization utilizing hybrid genetic algorithms［J］.Computer Engineering and Design，2007，28 （22）：5457－5460 （in Chinese）.［薛迎春，须文波，孙俊.基于遗传模拟退火混合算法矩形包络求解 ［J］.计算机工程与设计，2007，28 （22）：

5457－5460.］

［7］ZHAO Xiaohui，CAI Li，ZHANG Peng.Simulation of quantum cellular automata based on quantum genetic algorithm ［J］.Micronanoelectronic Technology，2011，48 （1）：3－9 （in Chinese）.［赵晓辉，蔡莉，张鹏.基于量子遗传算法的量子细胞自动机仿真方法 ［J］，微纳电子技术，2011，48 （1）：3－9.］

［8］Cho H，Swartzlander EE.Adder designs and analyses for quantum－dot cellular automata ［J］.IEEE Transactions on Nanotechnology，2007，6 （3）：374－383.

［9］Zhou Rigui，Xiao Tianru.A research on simulation engines of quantum－dot cellular automata［J］.J Comput Inf Syst，2013，9 （3）：977－985.

［10］WANG Sen，CAI Li，SU Fayuan.Design method based on quantum cellular automata ［J］.Nanoelectronic Device and Technology，2007，（44）4：171－174 （in Chinese）. ［王森，蔡莉，苏发院.基于量子细胞自动机的设计方法 ［J］.纳米器件与技术，2007，（44）4：171－174.］