融合运动幅度与方向特性的快速运动估计算法

万智萍

（中山大学 新华学院，广东 广州510520）

0 引 言

运动估计算法在对视频压缩时，其特有的块匹配方法与高效的预测模式使得在视频压缩领域被人们广泛的运用［1－4］。为了进一步减少运动估计算法耗时，人们相继提出了各种新的快速估计算法，例如三步搜索算法 （TSS）［5］、钻石搜索算法 （DS）［6，7］以及全搜索算法 （FS）［8］等；这 些算法虽然进一步完善了现有的压缩技术，但仍然存在着许多不足，如FS算法在对视频图像进行压缩时，虽能够得到较为清晰的视频图像但算法需要计算的搜索点太多；TSS算法与DS算法虽然能够利用运动矢量的中心偏置分布特性来提高算法的搜索速度，但当处理的视频运动幅度较大时，容易出现局部最优化现象。因此，为了弥补上述的不足，人们提出了UMHexagonS算法［9，10］，通过结合运动矢量的水平垂直偏置分布特性与半路中止条件，得到与FS质量相近而时间却缩短90%的运动估计效果。但通过对UMHexagonS算法的研究发现，该算法中仍然存在着不足，如在搜索过程中，未能充分利用视频图像的运动方向性和存在着一些多余的搜索点等；因此，本文通过优化起始搜索点的预测方式，并根据视频序列的运动幅度与方向特性［11］，提出了一种新的阈值运动估计算法，充分利用SAD 准则与图像的运动特性对视频图像进行分类；并结合改变搜索过程中的搜索长度与搜索模式，提出了具有自适应的方向搜索模式来对各类运动块进行处理，经测试，本文算法能够在保持视频图像的质量的情况下，有效减少算法搜索过程中的搜索点数。

1 自适应搜索长度

为了方便算法的计算。在运动估计算法中，将其搜索目标进行切割处理，而H.264标准算法中共有7种不同尺寸的分割块分别为：16×16、16×8、8×16、8×8、8×4、4×8、4×4，图1为这7种分割块的形式。

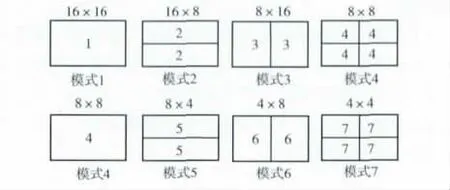
图1 H.264标准下的7种模式

而通过对传统算法的研究，我们可以发现在传统的运动估计算法中，为了得到清晰的视频图像，通常对图像中不同的分割块采用相同的搜索窗进行预测；虽然这样有效的降低了算法的复杂程度，但显然容易造成图像的搜索冗余，例如采用32×32搜索窗来对8×8的分割块和16×16的分割块进行搜索就容易出现搜索的冗余现象，从而降低了算法的搜索效率。

为了减少算法在搜索过程中的冗余现象的发生，本文针对不同大小的分割快模式，采用动态的搜索窗来定义各搜索模式的长度，其函数的表达式

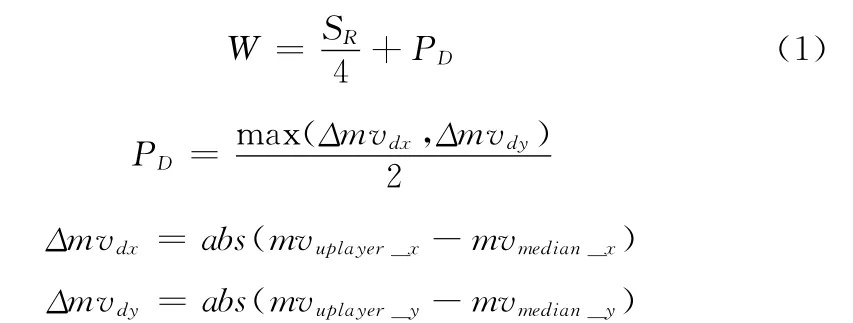
其中，SR为在算法中固定搜索窗的尺寸大小，mvuplayer＿x、mvuplayer＿y是上层预测时预测运动矢量中的水平分量与垂直分量，mvmedian＿x、mvmedian＿y是中值预测时预测运动矢量中的水平分量与垂直分量。通过采用上述方法，来减少算法搜索过程中多余的搜索点，从而为算法的进一步完善提供有利的条件。

2 起始搜索点的预测

在进行的运动矢量预测时，先使用中值预测，得到当前搜索点，并将其设为最佳点best，引入自适应的阈值Th1、Th2进行预先判断

公式

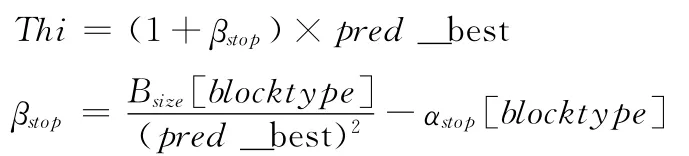
其中βstop 为块的尺寸，αstop为常数组，常数组αstop＝｛0.30，0.33，0.33，0.27，0.13，0.13，0.44｝；

通过在起始点的预测搜索过程中引入阈值，来到减少算法中的必要的搜索，从而节约了搜索的点数；在此过程中，对运动矢量幅度较小的采用菱形模板进行搜索；

3 运动类型分类

为了减少算法中的计算量与降低运动估计算法的算法复杂度，采用当前块与预测起始点对应块的像素值SAD 进行分类；SAD（s，c（m））为源视频信号s与编码视频信号c之间的绝对误差和，能够较好的反映视频图像的块运动幅度的大小，本文通过引入阈值λ1来对其进行判断。

其计算函数表达式，定义如下

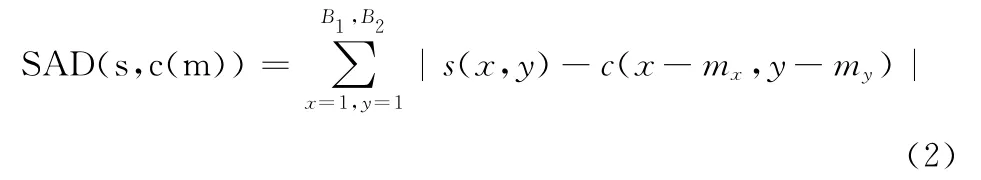
其中B1，B2＝16，8或4；s是当前编码的数据；c （m）是编码重建的参考帧数。

为了进一步提高算法的分类的准确性，根据视频的运动特性；本文引入运动的特性，令

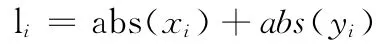
其中i的取值为1，2，3，4；得到运动特性的函数表达式：L ＝max｛l1，l2，l3，l4｝。

其函数的分类如下：

当SADP≤λ1时，可直接定为静止状态；

当λ1＜SADP＜λ2＆L ≤L1时，为运动幅度慢的运动块；

当（λ1＜SADP＜λ2＆L1＜L ＜L2）｜｜ （λ2≤SADP＆L ≤L2）时，则当前块为运动幅度中等的运动块；

当λ2≤SADP＆L2≤L 时，则当前块为运动幅度快的运动块；

其中L1、L2为预设的门限常数。

下面对阈值的取值进行定义，如下所示：

（1）阈值L1、L2根据多次试验最终总结出来经验，即当L1＝1，L2＝2时，其分离出来的运动块最为精确。

（2）若当前块的第一个P 帧内的块，则此时令阈值λ1＝512，否则令λ1＝a×REF＿SAD ，其中a为常数，在本文中a的取值为0.95，REF＿SAD 为参考帧对应位置块的SAD 最小值。

若λ1＜512，则λ1＝512

若λ1＞1024，则λ1＝1024

阈值λ2的取值则为λ2＝λ1＋256；

研究发现，对于视频图像的运动块，当其运动块运动幅值较小的时候，由于其搜索目标主要集中在搜索原点以及其附近，则直接对其进行小菱形搜索模式就能精确的得到搜索目标；而当运动幅值中等的时候，其搜索目标由于运动幅度大使其偏离模式原点，因此采用圆形搜索模式先对其进行初步的搜索，后进行菱形搜索模式进行缩小搜索范围，最终由小菱形搜索模式对其进行精确定位；当运动幅值较大的时候，其搜索目标点由于运动太过于激烈使其远离了搜索原点并分散在离原点较远的范围，而十字搜索模式能较好的对分布较为广的运动块进行搜索，因此可以采用十字搜索模式对其进行搜索，最后采用小菱形搜索模式定向精确搜索。其最终的分类处理方法如下所示：

当SADp≤λ1时，直接提前停止搜索；

当λ1＜SADp＜λ2＆L ＜L1时，采用菱形搜索模式；

当满足（λ1＜SADp＜λ2＆L1＜L＜L2）或者满足（λ2＜SADp＆L ＜L2）；则采用圆形＋菱形＋小菱形搜索模式；

当λ2＜SADp＆L2＜L时，采用十字＋小菱形搜索模式。

4 运动块的运动分布情况

在现实的生活中，采集回来的视频图像通常是沿着水平方向与垂直方向上进行扫描，为了验证运动块中搜索目标所分布的位置，本对QCIF 的3 个标准视频测试序列：news、foreman、coastguard分别进行仿真并取其平均值进行统计，其中news的空间细节比较少，并且运动较为缓慢，因此用来表示运动幅度小的运动序列；foreman虽然镜头与画面的背景一起运动，但其纹理复杂度一般，因此用来表示运动幅度中等的运动序列；coastguard运动形式丰富并且其纹理的复杂度极高，因此用来表示运动幅度很大的运动序列。在标准搜索窗下，得到的数据，表1 为通过仿真后各视频搜索目标所在位置平均概率表。

表1 搜索目标所在位置概率

由表1可以看到，搜索点在出现在预测中心的概率最高，高达60.05%；而其他则基本上集中在水平方向与垂直方向上；因此，本文在对搜索目标点的时候，主要将搜索重心集中在搜索原点 （0，0）、水平方向与垂直方向上，将上面的圆形搜索模式与十字搜索模式引入运动块的方向特性，提高算法估计效率。

5 方向性搜索模式

5.1 方向六边形搜索模式的选用

采用圆形搜索模式，圆形搜索模式包括三角搜索模式、正方形搜索模式以及正六边形搜索模式；而其中正六边形的搜索中心间隔最大且其覆盖面最广，有利于更为精确的搜索。

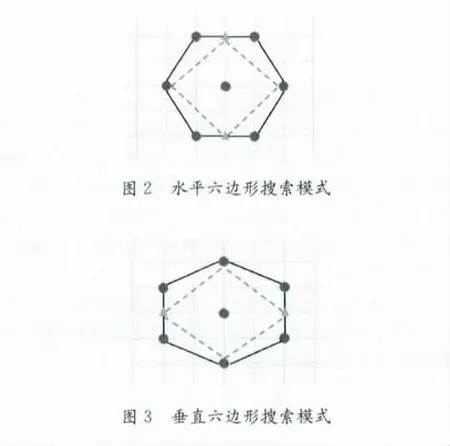
根据表1数据中搜索点的分布情况，则先进行搜索原点进行判断，如果不是最优点，则将正六边形搜索模式分为水平六边形搜索模式与垂直搜索模式，并采用式 （1）定义其搜索窗的长度；图2为水平六边形搜索模式，图3为垂直六边形搜索模式。

为了更好的对视频进行搜索，本文采用阈值判断算法将其进行选择如下所示：

令水平方向与垂直方向的相对二价距为Lx，Ly；

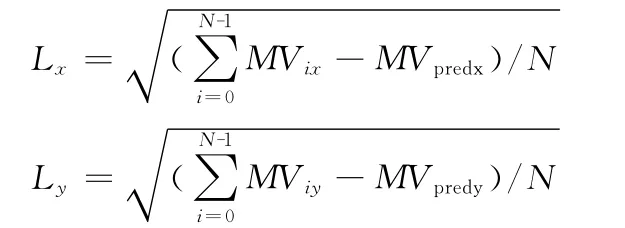
其中N 为运动矢量集的元素个数，MVix、MViy为MVi的水平与垂直方向的分量，MVpredx、MVpredy是MVpred在水平与垂直方向的分量；

当处于Lx＜λ3＜Ly时，说明在垂直方向上相对剧烈，即在该范围内可采用垂直六边形搜索模式进行搜索；

当处于Lx＜λ3＜Ly时，说明在水平方向上相对剧烈，即在该范围内可采用水平六边形搜索模式进行搜索。

5.2 非对称十字搜索模式的选用

为了更好的利用视频的方向特性［12］，本文将十字搜索模块分为两类：水平十字搜索模块、垂直十字搜索模块。在对视频进行搜索的时候，对其进行判断，判断搜索点是否在搜索中心，是则进行小菱形搜索；否则，根据最佳匹配点的位置来确定，根据运动方向函数来确定采用什么十字搜索模块进行搜索，并通过采用式 （1）定义其搜索窗的长度。图4为水平十字搜索模式，图5为垂直十字搜索模式，如下所示。

其中水平十字搜索模板，该模板在水平方向上的移动速度快于垂直方向，将其运用于具有水平特性的运动块上，可以明显加快水平方向上的搜索速度，并且减少对不必要点的匹配计算，提高运动估计速度。同理，垂直十字搜索模板也具有相同的效果；引入判断法则，将当前宏块运动估计得到的最佳运动矢量记为MV，则该运动矢量方向的计算方法

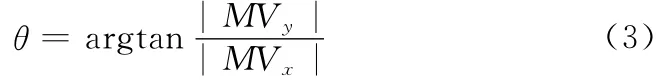
其中MVx、MVy分别为MV 的水平与垂直分量。

6 算法的流程

步骤1 起始搜索点的预测，先使用中值预测，得到当前搜索点，并将其设为最佳点best；引入自适应的阈值Th1与Th2，对其best进行判断：若best＜Th1；提前停止搜索；若Th1 ＜best＜Th2；跳到菱形模板搜索；若Th2＜best；则执行步骤2。

步骤2 根据运动类型自适应法，采用SAD 值与运动特性来对视频进行分类处理，当SADp≤λ1时，为静止模块，提前停住搜索；当λ1＜SADp＜λ2＆L ＜L1时，即为运动幅度小的运动块，则采用菱形搜索模式，后可以转至步骤7；（λ1＜SADp＜λ2＆L1＜L ＜L2）｜｜（λ2＜SADp＆L ＜L2）时，即为运动幅度中等的运动块，转至步骤3；当λ2＜SADp＆L2＜L 时，即为运动幅度大的运动块，转至步骤4；

步骤3 采用方向六边形搜索模式，通过比较Lx、Ly与阈值λ3的大小关系来选择方向六边形搜索模式；当Lx＜λ3＜Ly，使用垂直六边形搜索模式，当Lx＜λ3＜Ly，使用水平六边形搜索模式；经过方向六边形搜索模式后，采用菱形搜索模式进行进一步精确搜索，最后转至步骤5；

步骤4 采用非对称十字搜索模式，并通过式 （3）来获得水平分量与垂直分量的比例，来获得的θ 的范围；当＜θ＜π 4 时，采用水平十字搜索模式，当＜θ＜时，采用垂直十字搜索模式；经过十字搜索模式后，转至步骤5；

步骤5 小菱形模板反复搜索，得到运动矢量；

步骤6 输出MV。

7 仿真实验

本文在JM12.2平台上进行算法验证，采用的视频测试序列为代表不同运动剧烈程度的两种不同格式的6个标准序列：其中QCIF 格式的采用news、foreman、coastguard，而CIF格式采用akiyo、foreman、football；并设置编码帧数为60，参考帧数为5，帧率30，编码格式为IPPPP，QP值为32。各视频序列的分类，见表2。

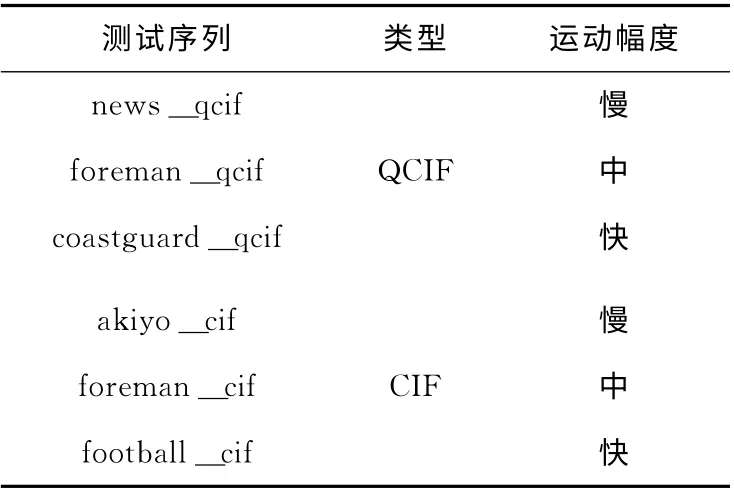
表2 各视频序列的分类

7.1 搜索点与搜索时间的比较

算法的搜索消耗时间可以用宏块中的搜索点数来衡量，其中搜索点数越少，其过程越简单，所花费的时间也就越少；因此，为了更好的验证算法在搜索方面的优越性，本文通过对比各算法间的搜索点数，体现算法在搜索方向的优势，经检测，得到表3为各算法每个宏块中的平均搜索点数数据表。

由表3可以清晰的看到，全搜索算法的搜索点数最多，而钻石搜索法由于有效的利用运动矢量的中心偏置分布这一特性来进行搜索，大幅度的减少了运动估计算法中的搜索点数，有表可以看到，其平均搜索点数相比全搜索算法减少了95%的搜索点数；UMHexagonS算法却在其基础上进一步提升，使搜索点数进一步减少；而本文算法的搜索点数比UMHexagonS算法的搜索点数将近一半，有效的证明了算法的优越性。表4为UMHexagonS算法与本文算法的耗时数据表。

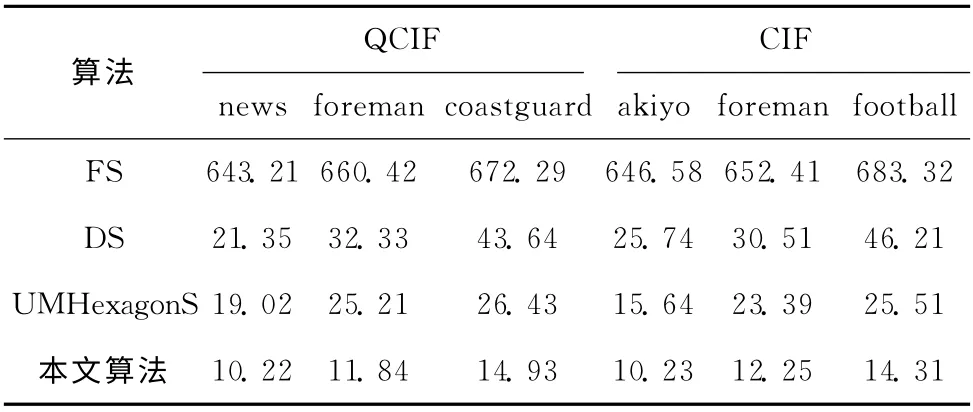
表3 各算法每个宏块平均搜索点数

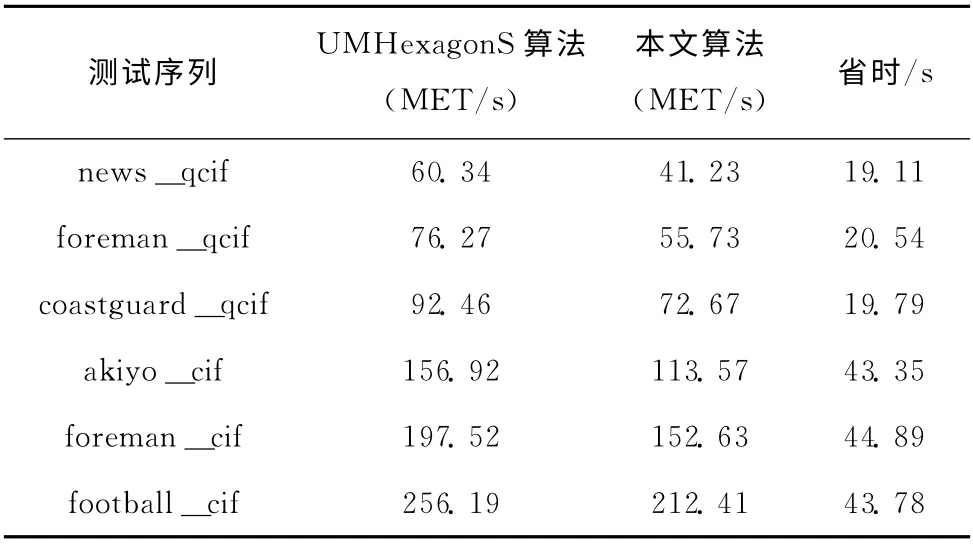
表4 UMHexagonS算法与本文算法的平均耗时

7.2 峰值信噪比的比较

本文采用的峰值信噪比计算公式如下所示

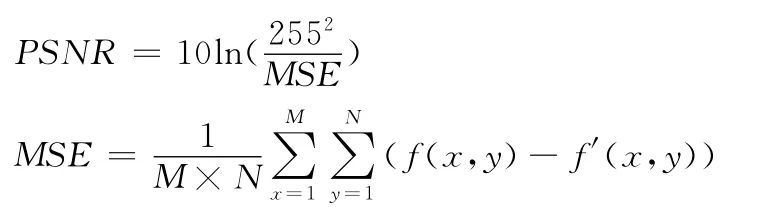
其中M，N 为视频图像的长和宽，f（x，y）为原始图像的像素灰度值而f′（x，y）为重构后的视频图像像素灰度值，其中所测得的PSNR 值越大，则表示的视频处理效果最好。通过检查，得表5为各算法的峰值信噪比数据表。

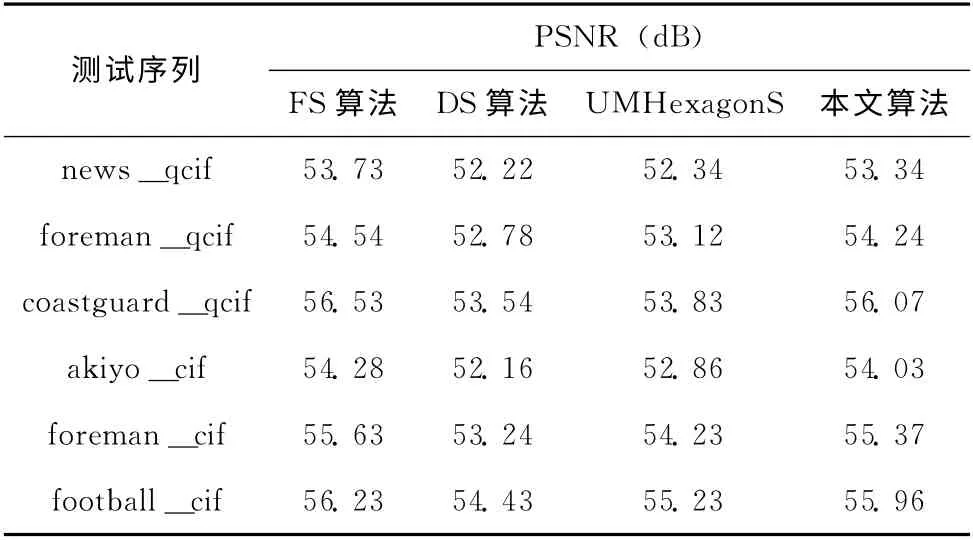
表5 各算法的峰值信噪比数据

由表5可以看到，本文算法所测得的峰值信噪比与全搜索算法的峰值信比相差无几，并且伴随着所测视频的运动幅度的变换，本文算法的PSNR 值依然与全搜索算法相同，其中最大的比全搜索差0.46dB，最少相差只有0.25dB；而钻石搜索法与UMHexagonS算法由于其算法的局部最优解，使得得到的视频质量受到视频运动幅度大小的影响。进而有效的验证了算法在视频保质的优越性。

为了检验算法的可行性，本文采用运动幅度相对较大点的football标准序列对以上算法进行测试，其中采用QP＝28；其仿真结果图如图6所示，图6为football第47帧各算法的主观效果对比图。

图6 football第47帧各算法的主观效果对比

当QP＝28时，通过采用FS、DS、UMHexagonS算法以及本文算法对football进行仿真的最终效果图，从图6我们可以看到，本文算法与DS、UMHexagonS算法相比，其解码图的效果与理想的FS算法的效果很接近，与预期的效果相符，具有一定的可行性。

8 结束语

本文提出一种融合运动幅度与方向特性的快速运动估计算法，充分调用运动块的SAD 值与运动特性进行分类，并结合方向搜索模式来减少算法中不必要的搜索点，到达算法的最优化。经实验，该算法能够在保证图像质量的情况下有效的减少算法中的搜索点数，进而大大减少算法花费的时间；而且在搜索的过程中不受图像运动幅度大小的影响，始终保持与全搜索算法相近的搜索效果。

［1］Juwon Byun，Jinha Choi，Jaeseok Kim.A fast multi－reference frame motion estimation algorithm ［J］.IEEE Transactions on Consumer Electronics，2010，56 （3）：1911－1917.

［2］LIU Shaowei，WEI Shouder，LAI Shanghong.Fast optimal motion estimation based on gradient－based adaptive multilevel successive elimination ［J］.IEEE Transactions on Circuits and Systems for Video Technology，2008，18 （2）：263－267.

［3］Sangkwon Na，Chong－Min Kyung.Activity－based motion estimation scheme for H.264 scalable video coding ［J］.IEEE Transactions on Circuits and Systems for Video Technology，2010，20 （11）：475－1485.

［4］Yasser Ismail，Jason B McNeely，Mohsen Shaaban，et al.Fast motion estimation system using dynamic models for H.264／AVC video coding ［J］.IEEE Transactions on Circuits and Systems for Video Technology，2012，22 （1）：28－42.

［5］Su Chungyen，Hsu Yipin.Reused SAD for partial search area in efficient three－step search algorithm ［J］.Journal of the Chinese Institute of Engineers，2007，30 （3）：537－543.

［6］Chatterjee S K，Chakrabart I I.Low power VLSI architectures for one bit transformation based fast motion estimation ［J］.IEEE Transactions on Consumer Electronics，2010，56 （4）：2652－2660.

［7］Po L M，Ting C W，Wong K M，et al.Novel point－oriented inner searches for fast block motion estimation ［J］.IEEE Transactions on Multimedia，2007，9 （1）：9－15.

［8］Sarwer M G，Wu Q M J.Efficient two step edge based partial distortion search for fast block motion estimation ［J］.IEEE Transactions on Consumer Electronics，2009，55 （4）：2154－2162.

［9］Xu Xiaozhong，He Yun.Improvements on fast motion estimation strategy for H.264／AVC ［J］.IEEE Transactions on Circuits and Systems for Video Technology，2008，18 （3）：285－293.

［10］Martin Schwalb，Ralph Ewerth，Bernd Freisleben.Fast motion estimation on graphics hardware for H.264video encoding ［J］.IEEE Transactions on Multimedia，2009，11 （1）：1－10.

［11］Takumi Kobayashi，Nobuyuki Otsu.Motion recognition using local auto－correlation of space－time gradients［J］.Pattern Recognition Letters，2012，33 （9）：1188－1195.

［12］Hannah M Dee，Anthony G Cohn，David C Hogg.Building semantic scene models from unconstrained video［J］.Computer Vision and Image Understanding，2012，116 （3）：446－456.