基于偏微分方程与边缘检测的图像去噪算法

张 帆

（河南工程学院 计算机科学与工程系，河南 郑州450053）

0 引 言

目前图像去噪的方法有很多种，传统的均值滤波、中值滤波等一些比较典型的空域去噪方法［1，2］，基于小波的去噪方法［3］。而近20年来，基于偏微分方程 （PDE）的方法在图像去噪中也得到了广泛的应用［4］。Perona和Malik［5］首次提出了经典的各向异性扩散P－M 模型，该模型由一个关于图像梯度模值的扩散函数控制图像的扩散程度，使图像在梯度模值小的区域进行大规模地扩散，在梯度模值小的区域行小规模地扩散。自P－M 模型的提出，出现了大量的基于偏微分方程的各向异性扩散的图像去噪方法研究［6－9］。基于二阶偏微分方程的扩散模型可以达到很好的去噪效果，但是由二阶偏微分方程处理得到的结果图像中会产生很明显的阶梯效应。该现象不仅会产生不良的视觉效果，而且会造成后续图像处理工作中对图像理解和分析的误判断。为了解决该问题，You和Kaveh首先提出了基于四阶偏微分方程的Y－K 模型，该模型使图像最终扩散为一个分段光滑的斜面，有效地避免了阶梯效应。尽管Y－K 模型不会产生阶梯效应，但该模型过度平滑图像的高频成份，包括边缘细节，而且在结果图中会产生孤立的脉冲噪声，即所谓的 “斑点效应”［10］。

梯度矢量场 （GVF）［11］是作为主动 轮廓模型［12，13］的 外力场提出来的，可以有效检测图像的轮廓边缘。但GVF的抗噪能力很弱，因此Ghita［14］等人提出一种改进的GVF场（INGVF）边缘检测算法，并把INGVF 引入到P－M 模型中。虽然提出的基于INGVF 的P－M 模型能得到更好的去噪算法，但由于二阶偏微分方程固有的阶梯效应，因此，本文将INGVF场引入到四阶Y－K 模型中，提出了基于边缘检测的各向异性四阶扩散模型，该模型不但消除了二阶模型的阶梯效应，而且能够使图像在梯度方向的扩散小于在边缘方向的扩散，从而在去除图像噪声的同时能更好地保留图像的边缘细节。实验结果表明，新的四阶PDE 模型不仅可以提高结果的峰值信噪比和平均结构相似度，而且能更好地保持图像的边缘特征。

1 边缘检测模型和四阶偏微分方程

1.1 INGVF边缘检测模型

INGVF是针对主动轮廓模型中的一种外力场——梯度矢量场 （GVF）做的改进。GVF是通过最小化能量方程

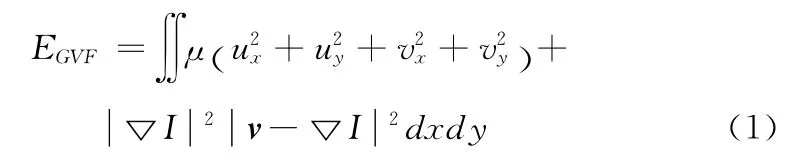
其中，f 是图像的边缘图；μ 用来调节式中第一项和第二项作用范围的权重。对式 （1）使用变分法得到对应的Euler方程

其中，Δ代表拉普拉斯算子。尽管GVF可以得到较好的边缘检测能力，但是仅限于无噪声或者噪声很小的情况中。GVF场的噪声鲁棒性极低，当图像存在噪声的时候，GVF模型会极大的受到噪声影响而使检测得到的边缘很不准确。另外GVF很难扩散到凹形区域，因此对凹形区域的边缘检测区域的边缘检测也极不准确。针对这种情况，Ghita提出了一种新的GVF场，通过最小化能量方程

其中IN（I）定义为噪声检测算子

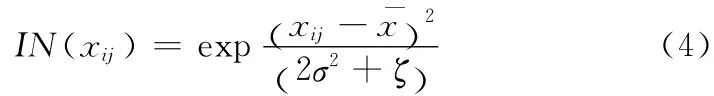
图1显示了GVF 和INGVF 在一幅噪声图像N（0，0，3），N（0，0，4）不同噪声等级中的效果。

为了对比GVF 与INGVF 的效果，我们选取相同的GVF和INGVF参数：μ＝0.2，迭代次数都为80次。从图中可以看出，INGVF可以能顺利进入深度凹陷区域，对噪声也很鲁棒。

1.2 四阶偏微分方程

为了得到较好的去噪效果并有效去除二阶偏微分方程中出现的阶梯效应，You和Kaveh首先提出了基于四阶偏微分方程的去噪模型。该模型的建立首先定义了一个关于图像灰度拉普拉斯的能量函数

图1 GVF和INGVF在噪声图像中效果

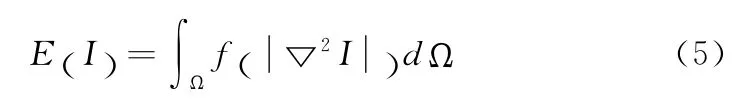
最小化该函数通过求解如下欧拉方程得到

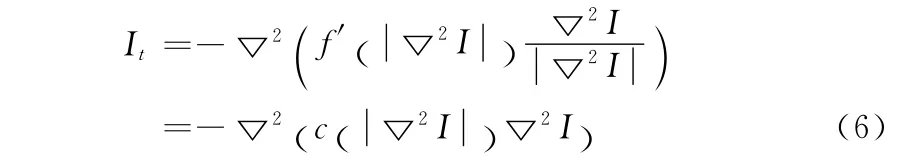
该方程将图像扩散为分段的光滑斜面，所以能有效地去除二阶模型中的阶梯效应并能够得到较好的去噪效果。但是该模型会过度平滑图像中的边缘，导致图像的边缘细节特征丢失。另外，在去噪过程中会在结果图中产生一些孤立的脉冲噪声，影响视觉效果。

2 基于边缘检测的四阶扩散模型

首先，对于图像引入其局部坐标系 （η， ξ） ，其中η 代表梯度方向，ξ代表垂直于梯度方向，即边缘方向。图像的空间坐标系 （x ，y） 与局部坐标系 （η， ξ） 的对应关系为

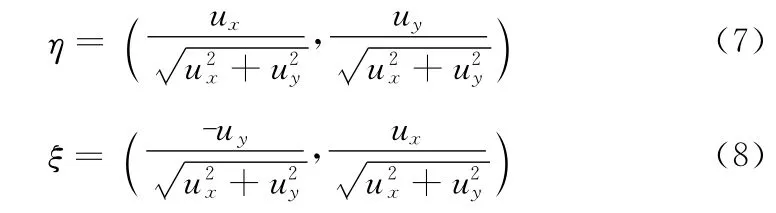
Y－K 模型是一个各向同性的扩散模型，它在梯度方向和边缘方向进行同等程度的扩散。将INGVF 模型引入到Y－K 模型中，使得改进后的模型为各向异性扩散的模型。图像I（x，y）在方向η和ξ 上求二阶导数可得到

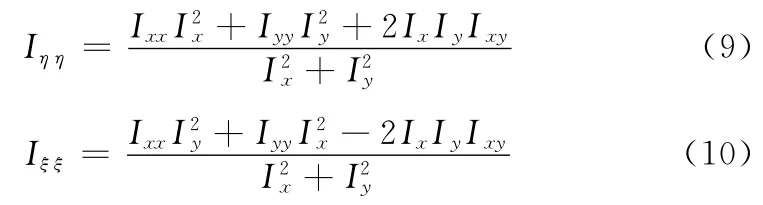
由方程 （6）和方程 （7）可以得出

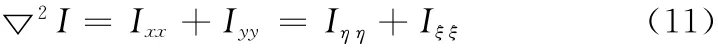
因此，为了使Y－K 模型可以达到各向异性的特性，YK 模型可以改写为

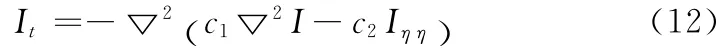
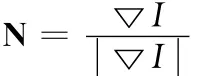
这就是本文提出的基于INGVF的各向异性扩散四阶模型。由于INGVF场可以在去噪迭代之前计算出来，因此迭代求解方程（14）时只需要从图像I中计算出单位梯度矢量，避免了计算二阶导数Iηη所引起的误差。该模型不仅具有各向异性的特性，而且其数值计算的稳定性也得到了提高。

在方程 （14）中，c1和c2的选取也会影响到模型的去噪效果。当c2＝0 时，则方程退化为原始Y－K 模型。当c1＜c2时，会使图像在整个梯度方向进行逆扩散，而在边缘方向进行正向扩散，这样进过多次的迭代后会破坏图像的原始特征。因此，在图像的整个区域，我们令c1＞c2，这样可以保持图像在整个区域都沿梯度方向和边缘方向进行正向扩散，并保持沿着梯度方向的扩散小于沿着边缘方向的扩散程度。从而达到保护边缘的目的。因此，在本文中，我们取扩散系数c1和c2为

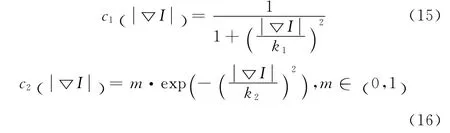
可以通过调节k1，k2和m 值的大小来得到最佳的去噪效果。图2给出了c1和c2随梯度模的变化关系，其中，扩散系数c1和c2的参数选取为k1＝k2＝3，m＝0.5，这就决定了模型 （14）为各向异性扩散的四阶滤波器。

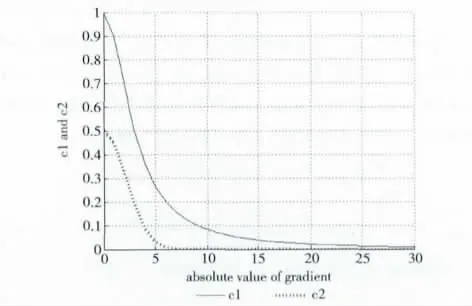
图2 c1 和c2 随梯度模的变化关系

3 实验结果

通过两组实验来展示模型 （14）的去噪效果和边缘保护能力，并和Y－K 模型进行比较。模型中参数取为k1＝k2＝7，m＝0.4，模型 （14）的时间步长是0.03，迭代次数为300，Y－K 模型的时间步长是0.2，迭代次数为500。图像去噪评价方法有很多种［15］，在本文中采用的是评价效果较好的PSNR 和MSSIM 两种方法，PSNR 的计算公式为

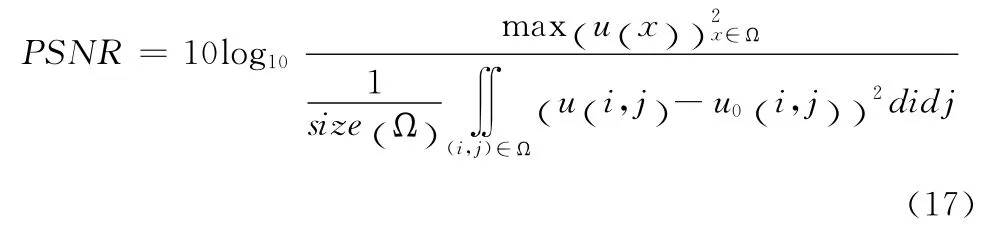
MSSIM 的计算公式为

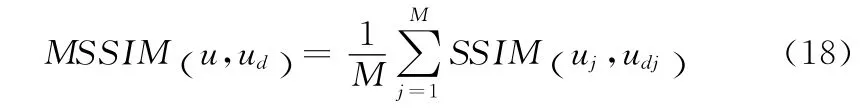
其中SSIM 是用来比较两幅图像的亮度，对比度和结构的相似度，它的计算公式为

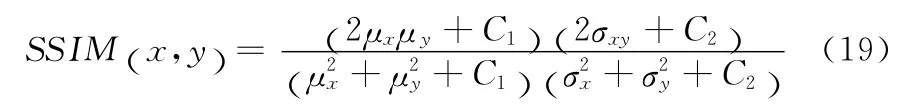
其中σx和σy代表图像x和y的方差。σxy是x和y的协方差。C1＝ K1（ ）L2，C2＝ K2（ ）L2，其中K1＝0.01，K2＝0.03，L代表图像灰度值的动态范围 （灰度图像L＝255）。计算结果的MSSIM 值越大，越接近1，代表去噪之后的图像与原始无噪声图像的相似度越高，去噪效果越好；而MSSIM 值越小，则代表去噪效果较差。

图3和图4给出了两个模型在Lena图像和Boat上的结果。图像大小均为512×512。图3和图4中第一行为整幅图像的去噪结果，为了更清晰地显示效果，我们截取了图像中的一部分放大显示在图中的第二行。

图像中的噪声均为方差为20的零均值高斯噪声。从图3和图4中均可以看到Y－K 模型的处理结果中边缘细节很模糊，同时会有一些斑点噪声的产生，整体视觉效果也较差。而经过本文模型处理的结果中边缘细节得到了更好地保留，比如在Lena图像中的羽毛部分，以及Boat图像中的字符 “LA2ORN”的边缘都更加清晰。图3 与图4 的数值比较见表1。

图3 Lena图像实验结果

图4 Boat图像实验结果

表1 图3、图4的PSNR 与MSSIM 的比较

可以看出本文方法可以得到更高的峰值信噪比和平均结构相似度。因此，从视觉效果和数值比较中都表明了本文模型比Y－K 模型具有更强的去噪效果和边缘保护能力。

4 结束语

将边缘检测算法INGVF 场引入到四阶Y－K 模型中，提出了基于边缘检测的各向异性四阶偏微分方程的模型。因为INGVF场引入了噪声监测算子，因此具有更强的噪声鲁棒性，同时具有进入深度凹陷区域强的特点，所以提出的模型提高了抗噪声和数值计算稳定性。而且该模型具有各向异性扩散的特性，从而有利于保持图像边缘细节。与Y－K 模型相比，该模型不仅具有更好的去噪效果，而且图像的边缘特征保护能力也得到了提高。

［1］DUAN Jinghong.A new varialbe－coefficient error diffusion method based on image edge detection ［J］.Computer Engineering and Science，2012，34 （7）：120－123 （in Chinese）.［段敬红.基于图像边缘检测的变系数误差扩散方法 ［J］.计算机工程与科学，2012，34 （7）：120－123.］

［2］CHEN Ying，YAO Heng，DAI Meng.Image colorization based on total variation and partial differential equation ［J］.Computer Engineering and Design，2012，33 （9）：3531－3534 （in Chinese）.［陈颖，姚恒，戴蒙.基于变分法和偏微分方程的图像彩色化方法 ［J］.计算机工程与设计，2012，33 （9）：3531－3534.］

［3］WANG Youming，WU Qing，WANG Wenqing.Operator custom－design decoupling algorithm for partial differential equations［J］.Computer Simulation，2013，30 （2）：261－264 （in Chinese）.［汪友明，吴青，王文庆.偏微分方程的算子自定义小波解耦算法研究 ［J］.计算机仿真，2013，30 （2）：261－264.］

［4］Aubert G，Kornprobst P.Mathematical problems in image processing：Partial differential equations and the calculus of variations［M］.2nd ed.New York：Springer，2006.

［5］Liu F，Liu J.Anisotropic diffusion for image denoising based on diffusion tensors ［J］.Journal of Visual Communication and Image Representation，2012，23 （3）：516－521.

［6］FU Jinhui，GUO Dinghui.A application of fourth order partial differential equation in image denoising ［J］.Chinese Journal of Engineer Mathematic，2012，29 （6）：791－798 （in Chinese）.［傅金辉，郭定辉.一个四阶偏微分方程在图像去噪中的应用 ［J］.工程数学学报，2012，29 （6）：791－798.］

［7］Li F，Shen C，Liu R，et al.A fast implementation algorithm of TV inpainting model based on operator splitting method ［J］.Computers and Electrical Engineering，2011，37 （5）：782－788.

［8］LIU Xilin，WANG Zewen，QIU Shufang.PDE－based image noise removal models based on Priwitt operator［J］.Computer Applications，2012，32 （12）：3385－3388 （in Chinese）.［刘西林，王泽文，邱淑芳.基于Priwitt算子的偏微分方程图像去噪模型 ［J］.计算机应用，2012，32 （12）：3385－3388.］

［9］ZHANG Fuping，ZHOU Shangbo，ZHAO Can.Novel color image denoising method based on fractional－order partial differential equation ［J］.Application Research of Computers，2013，30 （3）：946－949 （in Chinese）.［张富平，周尚波，赵灿.基于分数阶偏微分方程的彩色图像去噪新方法 ［J］.计算机应用研究，2013，30 （3）：946－949.］

［10］WANG Yu，XUE Hong.Applying oriented fourth－order partial differential equations to fluorescence microscopic image denoising ［J］.Computer Engineering and Design，2012，33（8）：3121－3124 （in Chinese）.［王瑜，薛红.基于方向四 阶偏微分方程的荧光显微图像去噪 ［J］.计算机工程与设计，2012，33 （8）：3121－3124.］

［11］ZHANG Yixiong，LI Xiying.Extraction of dumbbell shape object based on GVF and balloon improved model［J］.Computer Engineering and Design，2010，31 （9）：2131－2134 （in Chinese）.［张奕雄，李熙莹.基于GVF和压力Snake模型的哑铃型目标提取 ［J］.计算机工程与设计，2010，31 （9）：2131－2134.］

［12］DONGYE Changlei，ZHENG Yongguo，JIANG Donghuan，et al.SAR image segmentation based on global minimization Chan－Vese model ［J］Computer Engineering and Design，2012，33 （11）：4255－4258 （in Chinese）.［东野长磊，郑 永果，姜东焕，等.基于全局极小解Chan－Vese模型的SAR 图像分 割 ［J］. 计 算 机 工 程 与 设 计，2012，33 （11）：4255－4258.］

［13］ZHOU Liangfen，HE Jiannong.Weak interactive waterside line extraction new algorithm ［J］Computer Engineering and Design，2013，34 （4）：1442－1445 （in Chinese）.［周 良芬，何建农.弱交互式水边线提取新算法.［J］.计算机工程与设计，2013，34 （4）：1442－1445.］

［14］Ghita O，Whelan P F.A new GVF－based image enhancement formulation for use in the presence of mixed noise［J］.Pattern Recognition，2010，43 （8）：2646－2658.

［15］LI Hang，LU Yang，CUI Huijuan，et al.Image quality assessment based on frequency domain based strural similarities［J］Journal of Tsinghua University，2009，49 （4）：559－562 （in Chinese）.［李航，路羊，崔慧娟，等.基于频域的结构相似度的图像质量评价方法 ［J］.清华大学学报，2009，49 （4）：559－562.］