基于斜率约束插值的燃油流量特征提取方法
2014-12-23孙文柱曲建岭周胜明邸亚洲海军航空工程学院青岛校区山东青岛266041
孙文柱,曲建岭,周胜明,邸亚洲,高 峰(海军航空工程学院 青岛校区,山东 青岛266041)
0 引 言
准确的飞机状态监控可以发现飞机的状态变化趋势,从而有效保障飞行安全。现有飞机广泛安装有飞参记录系统 (flight data recorder,FDR),利用FDR 记录的飞参数据监控飞机状态能够实现以较低的成本长时间较完整地监测每架飞机,是一种可行性较高的飞机状态监控手段。
燃油流量是描述飞机发动机运行状态的主要参数之一,通过监测同等状态下的燃油流量的变化趋势可以监控飞机发动机性能退化程度。然而目前大多数机型虽然安装有燃油流量计,却不实时记录燃油流量值。因此利用飞参数据中记录的剩余燃油量获取燃油流量特征是一种有效的手段。目前已有许多学者对基于飞参数据中发动机状态参数和环境参数的燃油流量提取方法进行了研究,例如:文献 [1]采用多元线性回归方法对波音737-700飞机巡航段的燃油流量进行了回归建模,适用于发动机巡航稳定阶段燃油流量的计算,但该方法无法完成整个飞行架次的燃油流量提取;文献 [2]以发动机运行参数为输入,采用BP 神经网络燃油流量模型辨识的方法预测飞行全过程的油耗,但使用该方法获得的燃油流量与发动机运行参数存在相关性,不适用于飞机性能的综合监控。本文提出一种飞参数据中的剩余燃油量中提取燃油流量的方法,该方法通过对飞参数据中的离散剩余燃油量进行数据清洗及插值得到连续的剩余燃油量曲线,而后求取剩余燃油量曲线对时间的变化率提取出燃油流量。
飞参数据中可用于飞机状态监控的数据可以定义为3种类型:累积量、瞬时状态量和瞬时变化量。瞬时状态量指在不受外力情况下保持不变的量,如速度、角速度等;瞬时状态量的一次积分为累积量,如高度、距离、角度等;瞬时状态量的一阶导数为瞬时变化量,如各向加速度。累积量一般不可直接用于监控飞机状态;瞬时状态量常用于多参数组合监控,如航空发动机转子固定转速下的排气温度和滑油压力;瞬时变化量可以用于参数的极值监控,如飞机接地时刻过载监控。在基于飞参数据的飞机状态监控过程中,为了充分挖掘飞参数据参数中的有用信息,发挥每个飞参数据参数的作用,常需要进行3类参数间的转化。将瞬时状态量转化为累积量或将瞬时变化量转化为瞬时状态量的问题叫做一次积分量特征提取问题。将累积量转化为瞬时状态量或将瞬时状态量转化为瞬时变化量的问题叫做一阶导量特征提取问题。本文致力于解决一阶导量特征提取问题,并对一种典型的该类问题——从剩余燃油量飞参数据中提取燃油流量进行了详细描述。
1 剩余燃油量的数据清洗
本文以飞参记录系统记录的剩余燃油量为研究对象,此剩余燃油量参数的采样频率为2Hz,量程0~12000 升,每个采样值以9个二进制位存储,采样分辨率约为25升。某架次完整飞行过程的剩余燃油量记录值如图1所示,图1中可以看出,由于采样分辨率较大,剩余燃油量数据基本呈阶梯状单调递减的趋势。但在个别位置会出现偏离真实值较大的野值点 (6500s左右)和二值间反复变化的波动点(775s左右)。野值点的产生原因一般为线路间接触不良或较大的电磁干扰,而波动点是由剩余燃油量的原理性误差产生的。该型飞机剩余燃油量G 的计算公式为
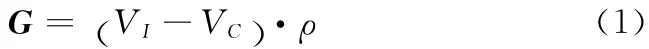
式中:VI——燃油 初 始 值;VC——燃油耗 量;ρ——燃 油密度。
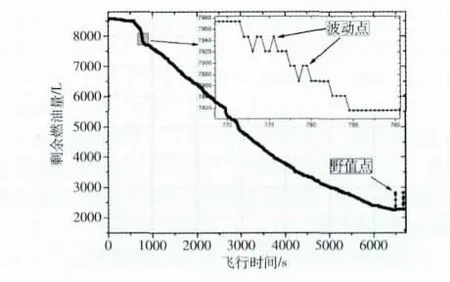
图1 飞参数据中的剩余燃油量数据
VI需要在每飞行架次前人工装定,因此对于一个架次来说,VI是恒定的。VC由叶轮式耗量传感器输出脉冲累积产生,因此VC一定是单调增加的。ρ为大气静温T 的函数,即ρ=Θ(T),而T 由飞行过程中的全压和静压解算产生,因此ρ是实时变化的。实时变化的ρ会导致计算所得的剩余燃油量数值偶然增大,经采样后就形成了剩余燃油量中的波动点。
真实剩余燃油量一定是随飞行时间的增加而减少的,即剩余燃油量数据应具有单调递减性。但野值点和波动点破坏了剩余燃油量的单调递减性,因此需要对剩余燃油量数据进行清洗以去除野值点和波动点,增加剩余燃油量数据的精度[3]。对于野值点的处理采用文献 [4]所述参数变化率失真法进行野值点判别,判别后利用前值替补后值法对野值点进行修正。波动点的去除采用中值滤波算法,具体内容参见文献 [5]。由中值滤波的原理可知,要保证中值滤波后的数据单调,只需要保证窗口滑动过程中进入窗口的数据值小于等于流出窗口的数据值。剩余燃油量在除少数波动点外,趋势上是单调递减的,只要使用窗口宽度足够大,就可以保证窗口滑动过程中进入窗口的点小于等于流出窗口的点,从而完全去除剩余燃油量数据中的非单调点。为检验不同窗口宽度下中值滤波去除剩余燃油量波动点的效果,对现有1280架次飞参数据中的剩余燃油量数据进行统计分析,剩余燃油量数据中波动点占所有采样点的比例随中值滤波窗口宽度的变化规律如图2所示。从图2中可以看出,采样点中波动点所占的比例随中值滤波窗口宽度的增加而减少,当窗口宽度增大到107 时,波动点所占的比例降为0。因此,在去除剩余燃油量波动点过程中,只需要将中值滤波的窗口宽度设置为大于等于107的奇数就可以保证完全去除剩余燃油量中的波动点。
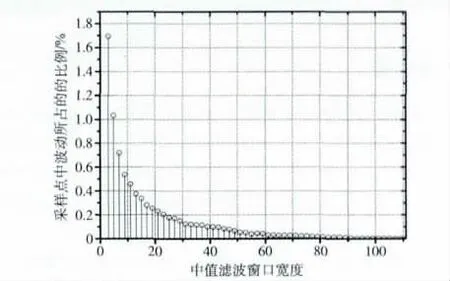
图2 剩余燃油量数据中波动点占所有采样点的比例随窗口宽度的变化规律
剩余燃油量数据中带有野值点和波动点的数据进行清洗的结果如图3所示,从图3中可以看到,604s处附近有野值点存在,经过去除野值点运算后野值点消除,618~632s处、646~650s处和673~693s处均存在不同程度的波动点,使用窗口宽度为107的中值滤波算法进行滤波后波动点消除,经过数据清洗的剩余燃油量数据呈严格阶梯递减状。
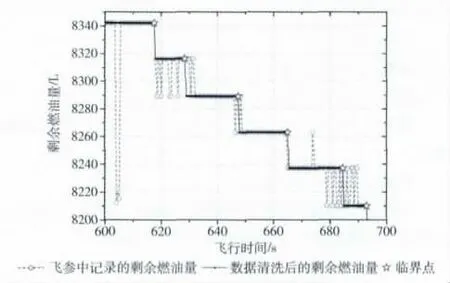
图3 剩余燃油量的数据清洗
2 剩余燃油量的插值
记数据清洗后剩余燃油量中数值序列为
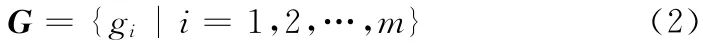
因此G 的形式为阶梯状递减,而真实的剩余燃油量应为连续递减,因此可以在每个阶梯上选择一个临界点以代替此阶梯上的所有值。
定义 如果样本点满足

则称该样本点为临界点 (见图3)。
图3标明了临界点的位置,临界点位于每一个阶梯的末尾,其包含了剩余燃油量递减过程中的所有信息量,因此可以舍弃临界点以外的所有采样点,只对临界点插值即可得到连续的剩余燃油量估计曲线。
插值方法的选择会较大程度上影响特征提取结果的精度。经总结,对临界点插值的方法需满足如下要求:
(1)插值所得的曲线需可导;
(2)插值曲线中的高频分量应尽量低以减少特征提取结果的震荡幅度;
(3)插值方法需保持临界点的单调性,且插值曲线斜率的绝对值应大于某常数,其物理意义为燃油流量始终大于飞机发动机最小稳定工作状态时的供油量。
综合以上3点要求,在临界点的插值过程中应选择一种低阶多项式的Hermite插值方法,且该插值方法应具有约束插值斜率的功能。现有对曲线斜率可调插值方法的研究主要集中于保单调插值方法[6-13],能够进一步限制斜率取值范围的方法国内外未见发表。本文在研究现有保单调插值方法的基础上对二次样条插值方法进行改进,提出一种适用于剩余燃油量临界点插值的斜率约束二次样条Hermite插值方法。
首先来讨论一下两点间的二次样条Hermite插值问题,这是二次样条Hermite插值问题的基础。
问题1:给定两点P1=(t1,z1)和P2=(t2,z2),(t1<t2)。假设s1和s2分别为点P1和P2处的插值斜率。寻找一个函数f ∈C1[t1,t2],使得

以下定理表明,在特定条件下,问题1 可以使用二次多项式样条解决。
定理1 问题1可以使用二次多项式样条解决的充要条件为

式中:Δ=(z2-z1)/(t2-t1)。
证明:结论是显然的。
当式 (5)成立时,两结点间的插值方式如图4 (a)所示,区间[t1,t2]上的插值函数为
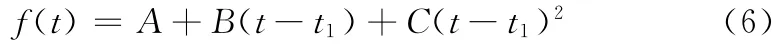
其中,A =z1,B =s1,C =(s2-s1)/2(t2-t1)。
当式 (5)不成立时,两结点间的插值方式如图4 (b)所示,需要对区间增加一个细分点ξ,珋s为细分点处的斜率

其中,a=s1-Δ,b=s2-Δ。
区间[t1,ξ]上的插值函数为
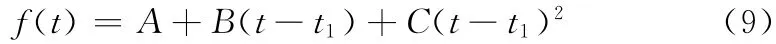
其中,A =z1,B =s1,C =-s1)/2(ξ-t1)。区间[ξ,t2]上的插值函数为
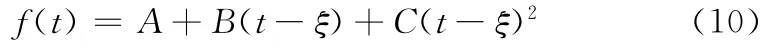
其中,A =z1+(ξ-t1)(珋s+s1)/2,B =珋s,C =(s2-)/
2(t2-ξ)。
在点列的插值问题中,每相邻的两点可以看做一个两点间的插值问题,并用定理1解决。
具有斜率约束的插值可以描述为以下问题:
问题2:给定点列
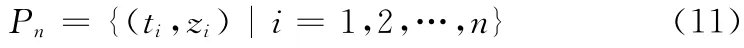
满足
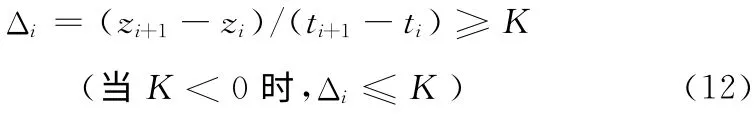
式中:K——斜率约束系数。
寻找一组插值函数f ∈C1[t1,tn]使得
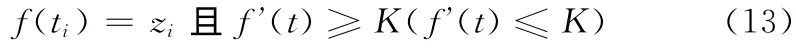
以下定理可以解决问题2。
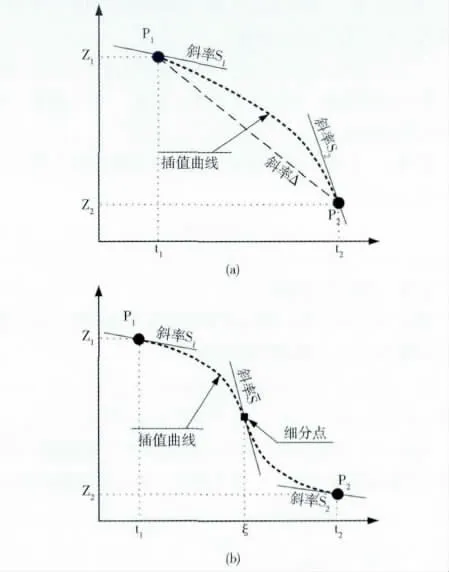
图4 两点间的二次样条Hermite插值

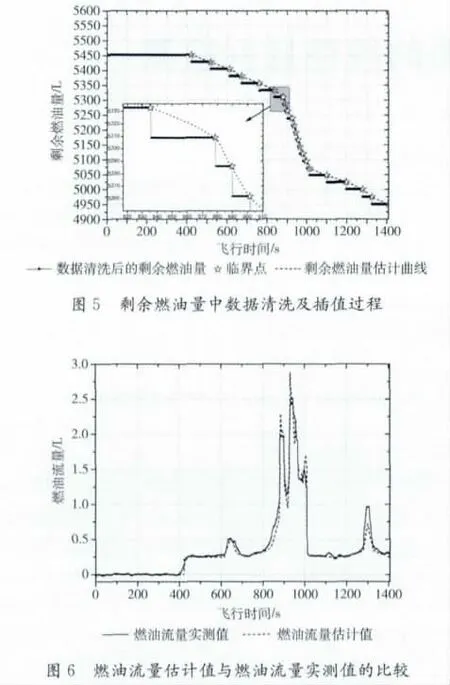
定理2 当插值点处的斜率满足时,问题2可以在定理1框架内解决。式 (14)中,si为点Pi处的斜率。
证明:不失一般性,我们假设Pn单调增,令

(1)当a+b=0时,式 (5)成立,区间[ti,ti+1]内无细分点,因此
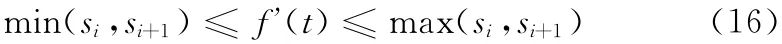
由式 (14)可得si≥K,所以f'(t)≥K;
(2)当a+b≠0且a·b≥0时,将式 (14)代入式(8)可得

因此,f'(t)≥min(si,,si+1)≥K;
基于以上讨论,给出一种斜率约束的二次样条Hermite插值算法如下:算法1:
步骤1 读入点列;
步骤2 由式 (14)计算si;
步骤3 由式 (7)~式 (10)计算pi和pi+1间的插值函数fi;
将算法1应用于临界点构成的点列GC上可以得到连续的剩余燃油量曲线,从而燃油流量估计值为

3 实例分析
在某一架次飞机地面试车过程中对燃油流量进行了精确测量,选取该架次实测燃油流量可以对本文提出的方法进行验证。已知该型飞机燃油流量最低值约为0.245L/s,因此斜率约束二次样条Hermite插值算法中取斜率约束系数K=-0.245,数据清洗过程中中值滤波窗口宽度为107。剩余燃油量数据清洗及临界点插值过程如图5所示,从图5中可以看出:数据清洗过程去除了剩余燃油量中的野值点和波动点,插值后的剩余燃油量曲线连续平滑并单调递减。燃油流量估计值与燃油流量实测值的比较如图6所示,实线为燃油流量实测值,虚线为燃油流量估计值,从图6中可以看出:发动机自423s发动机开车后,燃油流量估计值取值均大于0.245L/s,且燃油流量在0.245L/s附近时燃油流量估计值与实测值拟合程度很高,说明斜率约束的二次样条Hermite插值有效保证了插值斜率范围和燃油流量估计值范围。在880s到1000s区间内燃油流量值较高,此时燃油流量估计值与实测值拟合程度稍差。由此可以看出,本方法通过约束剩余燃油量的最小斜率,增加了燃油流量较低时的预测精度。
燃油流量的估计精度可以由相对预测误差 (relative prediction error,RPE)来衡量,相对预测误差的计算其公式为

通过计算得到:本实验中燃油流量特征提取方法的RPE为4.13%,其中燃油流量值低于1.0L/s部分RPE 为1.53%,高于1.0L/s部分RPE 为8.61%。当燃油流量值较高时,燃油流量估计值与燃油流量实测值相差较大,这是由于剩余燃油量在测量时即存在误差 (原理误差、安装误差、传输误差、干扰误差等),这部分误差在此方法中不能被有效滤除。当燃油流量值较低时,燃油流量估计值与燃油流量实测值相差较小。这说明斜率约束的燃油流量插值方法有效抑制了燃油流量值较低部分的误差,提高了燃油流量估计的精度。因此,利用该方法得到的燃油流量值较适合于的状态监控。
4 结束语
本文研究了从参数中提取其一阶导量的特征提取问题,并在从剩余燃油量中提取燃油流量过程中进行了实现,形成了一种燃油流量特征提取方法。在剩余燃油量的数据清洗过程中,引入了中值滤波理论,实验结果表明当窗口宽度达到一定值时,中值滤波可以完全去除剩余燃油量中的波动点。在插值环节中,本文设计了斜率约束二次样条Hermite插值方法有效保证了所求燃油流量的取值范围。实例分析结果表明,该估计方法得出的燃油流量值与实测燃油流量值在发动机低转速条件下具有较高的重合程度,估计精度较高,适用于所有飞参记录系统中记录了剩余燃油量的机型,具有较高的应用价值。同时,本文提出的方法对其他一阶导量特征提取问题具有借鉴作用。
[1]GENG Hong,JIE Jun.Aviation fuel flow regression model of aircraft cruise based on QAR data [J].Aeroengine,2008,34(4):46-50 (in Chinese).[耿宏,揭俊.基于QAR 数据的飞机巡航段燃油流量回归模型 [J].航空发动机,2008,34 (4):46-50.]
[2]LIU Jing.The aircraft fuel estimation model based on flight data analysis[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2010 (in Chinese). [刘婧.基于飞行数据分析的飞机燃油估计模型 [D].南京:南京航空航天大学,2010.]
[3]LI Yingying,TAN Guangyu,QU Jianling.Prehandling research of flight parameter strange points based on matlab digital filtering technique [J].Electric Machines and Control,2009,13 (1):135-138 (in Chinese). [李映颖,谭光宇,曲建岭.飞行记录参数奇异点的处理 [J].电机与控制学报,2009,13(1):135-138.]
[4]WU Jiangang,CHEN Zhiwei,LI Shulin,et al.Study on computer processing of recorded flight data[J].Computer Simulation,2007,24 (2):18-21 (in Chinese).[吴建刚,陈志伟,李曙林,等.飞参记录数据计算机处理的有关问题研究 [J].计算机仿真,2007,24 (2):18-21.]
[5]Gonzalez R C,Woods R E.Digital image processing [M].3rd ed.New Jersey:Pearson,2010.
[6]Hussain M Z,Sarfraz M,Hussain M.Scientific data visualization with shape preserving C1rational cubic interpolation [J].Eur J Pure Appl Math,2010,3 (2):194-212.
[7]Volkov Yu S,Bogdanov V V,Miroshnichenko V L,et al.Shape-preserving interpolation by cubic splines[J].Mathematical Notes,2010,88 (5):798-805.
[8]Sarfraz Muhammad H M Z.Hussain maria shape-preserving curve interpolation [J].International Journal of Computer Mathematics,2012,89 (1):35-53.
[9]ZHU Xiaolin,GE Chuanfeng.C~3convex T-B interpolating curve and an algorithm for shape preserving interpolation [J].Journal of Engineering Graphics,2009,30 (6):76-82 (in Chinese).[朱晓临,葛传丰.连续的保凸T-B插值曲线及保形插值算法 [J].工程图学学报,2009,30 (6):76-82.]
[10]Feng Renzhong L F.A shape-preserving quasi-interpolation operator satisfying quadratic polynomial reproduction property to scattered data [J].Journal of Computational and Applied Mathematics,2009,225 (2):594-601.
[11]Yong J P,Min C.A survey on shape preserving interpolation[C]//International Conference on Digital Object Identifier,2012:2521-2523.
[12]Chen Z,Su K.Research on a class of shape-preserving quasiinterpolation functions [C]//2nd International Conference on Digital Object Identifier,2010:1442-1445.
[13]Meng T.A shape preserving rational cubic interpolation spline[C]//2nd International Conference on Digital Object Identifier,2010:1-4.
