改进的基于位平面的图像加密算法
2014-12-23张雪锋
徐 超,张雪锋
(西安邮电大学 通信与信息工程学院,陕西 西安710061)
0 引 言
在当前的通信媒介中,数字图像因其存储方便、传输快捷且能给人以视觉直观感受等优势已成为信息传输的主要形式,并广泛应用于个人电子相册、医学图像传输、军用图像传输等场合。但同时这也为不法分子利用网络获取未授权数据提供了渠道。图像合法拥有者为了保护自身的利益,就需要可靠的图像数据加密技术。也正是因为如此,图像加密技术是目前研究最为广泛的领域之一。当前图像加密的技术可谓种类繁多,总的归结为以下几类:像素置乱,像素置换,以及以上两种方法的综合使用。每种加密方法都具有其各自优缺点,近年来如文献 [1]中所采用的基于位平面的图像加密算法因其具有的独特优点被很多学者广泛研究。
本文给出一种改进的基于位平面的图像加密算法,在采用文献 [1]所提出算法将图像按位面划分并对行列分别进行排序处理后,作为改进,本文给出一种作用于各位平面的置乱处理算法,本算法的改进在于不仅使用了传统置乱处理中的扩散思想,并在置乱过程中引入了混沌元素以增加加密算法的密钥空间。其基本思路为将各位平面等分为4份,然后将每个部分的值分别采用固定的方法扩散到整个位平面中去,同时定义出4 个集合与4 种排序方法,引入混沌序列后用加入的混沌元素来控制扩散排序方法。相比于文献 [1]中对各位平面采用猫脸变换,本文所采用的算法在密钥空间上具有较强的优势,具有较强的抗穷举攻击能力,以此使得穷举攻击理论上不再可能。实验结果表明,该算法具有较好的抗统计攻击和穷举攻击的能力,同时具有较强的抗剪切攻击的能力。
1 算法基础
1.1 混沌系统
1.1.1 Logistic映射
由于混沌序列的一些特性,使得其很适合来被用作序列加密。到目前为止,已经有很多种混沌系统被人们所发现,这里首先描述一下Logistic混沌系统的形式。其标准形式见式 (1)

其中,当0<μ <4 时,x0∈[0,1],μ ∈(3.5699456,4]时,系统处于混沌状态,生成的序列具有对初始值和参数敏感的特性,适合用来做序列加密的序列生成。
1.1.2 Chebyshev映射
与Logistic映射类似,Chebyshev映射具有以下形式
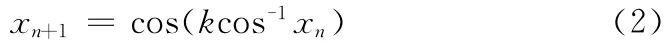
其中,当xn∈[-1,1]且K >2时系统进入混沌状态,同样可被用来进行序列加密。
1.1.3 Arnold变换
Arnold变换是V.J.Arnold在研究环面上的自态时提出的,俗称猫映射。为了将其方便地使用到图像加密中并且保留其一些有用的特性如混合性质和对初始参数敏感的性质,常常在使用前对其进行离散化处理,经处理后的猫映射表达式见式 (3)

其中,N 为正方形图像的长或宽,而p 和q 则可以作为加密密钥来保存,mod N 表示对N 取余数。猫映射为混沌映射,它具有非常典型的产生混沌运动的几个特性:拉伸和折叠,除此之外它还有可逆性和周期性,由于猫映射的混沌运动的特性,使它比较适合于二维数字图像的置乱处理。
1.2 图像加密的基本流程
引言中已经提到当前常用图像加密算法主要分为3类,一些传统的如猫映射,面包师变换等均属于像素置乱加密算法。由于单纯置乱处理仅对图像各点像素的位置进行保密规则的置乱处理而并不改变其像素值因此有较低运算复杂性的优势,但是其缺点也是很明显的,归结为一下3类:
(1)由于像素置乱处理并不改变各点像素值,因此其并不改变原始图像的直方图信息,因此在抵抗统计分析攻击时其效果不好;
(2)由于传统置乱算法的特性所决定,其具有周期性的特点,即对图像迭代使用该置乱算法后会在固定轮次后得到原始图像;
(3)传统像素置乱算法密钥空间不足,如猫映射中密钥p 和q 均为整形数类型,其抗穷举攻击的能力较弱。
作为弥补以上所述不足,往往将像素置换处理配合置乱处理来进行加密。由于像素置换处理能改变各点的像素值,且能够配合置乱处理来克服以上所提到的3 种不足,因此在加密处理中被广泛的使用。目前一些常见的置换处理基本思路为由密钥控制来生成若干序列 (包括伪随机序列和混沌序列等),并由这些序列通过与原始像素值进行XOR,ADD 等操作来改变各点的像素值。然而,由于传统像素置换处理所采用的操作特性,其对计算机操作而言是一个很耗时的过程。时间复杂度也是对一个加密算法的评价标准,为了克服传统置换处理的一些缺陷,文献 [1]提出了一种基于位平面的像素置换算法,该算法包括两个部分,即对原始图像扩展后得到的位平面分别进行行和列的排序操作以及排序完后再分开为8个位平面和分别对各位平面进行的保积混沌映射置乱处理。第一部分的大概步骤如下:
步骤1 通过密钥控制来生成一组混沌序列 (文献 [1]中使用Chebyshev映射),并去掉其前面若干项记为X。
步骤2 将所得到的混沌序列按大小进行升序排列,得到一组新的序列记为Y。
步骤3 将开始得到的序列X 中的确定数目的项与原始图像扩散后的位平面的行一一关联,并将各行按照对应的属于序列X 中的各项在重新排序后的序列Y 中所处的位置关系进行重新排序。
步骤4 对位平面的各列也同样按照上述方法通过另一个混沌序列的8*N 项来控制进行排序,N 为原始图像像素的列数。
文献 [1]中加密算法的第二步对各层进行保积混沌映射变换主要采用上节所介绍到的猫映射变换,通过8组各不相同的密钥来控制猫映射变换对各层位平面进行置乱处理。
由于本节开始已经分析到,传统的猫映射变换具有固有的缺点,为了克服其在图像置乱处理操作中密钥空间较小以及具有较小周期的缺陷,本文给出一种改进的置乱方法,将其替代猫映射变换应用到文献 [1]加密算法的第二步中。
1.3 改进的置乱算法
本文以图像分块置乱为基本思想,给出一种改进的算法,为传统置乱操作加入了混沌序列元素以改善其性能。实验结果表明,本文所给出置乱算法较传统如猫映射变换和面包师变换等算法具有更大的密钥空间及更好的加密效果。作为改进,在不改变传统算法中分块,穿插和扩散的总体思路的基础上,可以采用以下办法,即每轮都对分块扩散后的点进行不同的排序方法,如图1所示。

图1 4种排序方法
为了增加密钥空间以及让算法具有更好的加密效果,可以先将排序后的每一个位平面的按照图2分割为4等份后按照所处位置进行扩散,扩散后的点采用何种排序方法可以由一个特定的混沌序列来控制,具体控制方法为:生成一个混沌序列,获取从某一项开始的4个项,这4个项分别与该位平面的4个等分相对应,定义4个等大小的集合,将这4个混沌序列值判定到4个等大小的集合内,该4个集合又与图1中提到的4种排序方法相对应,位平面每轮扩散后采用的排序方法为与其相扩散前所处位置对应的混沌序列所判定到的那个集合相关联的那个排序方法。直到将位平面中所有像素进行按规则扩散及排序后开始第二轮置乱,使用混沌序列中第一轮置乱所使用的4个项之后的连续4个项做为参数,与第一轮置乱后的位平面再划分的4等份一一关联,同样适用第一轮置乱的方法判定后置乱,以此方法迭代置乱各位平面。
集合划分法的基本思路为:每次迭代置乱将选取Logistic混沌序列中上轮置乱所使用的序列值的之后连续4项乘以256后取整,即可将其划分到以下4个集合中的某一个。

进行排序处理后的位平面的分割及扩散方法如图2所示,框图代表整个位平面。
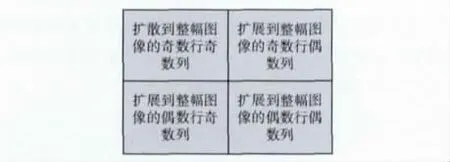
图2 分割及扩散方法
对每一个位平面的置乱算法的具体步骤如下:
步骤1 利用Logistic混沌系统生成一个混沌序列,由加密者控制选取该混沌序列中的某一项开始的4个连续值设为a(1),a(2),a(2),a(4),作为第一轮置乱使用。
步骤2 如式 (4)划分4个集合,将这4个集合与图1中的4种排序方法相关联。如A 与方法一项关联,B与方法二项关联等。
步骤3 将该轮置乱所用的4个混沌值乘以256以后划分到式 (4)所示4个集合中。
步骤4 如图2所示方法,将上一轮置乱后的位平面分为4个等份,分别记为f1(x,y),f2(x,y),f3(x,y),f4(x,y),与本轮置乱所用混沌序列的4 个项一一关联起来,如a(1)关联于f(1)1(x,y),a(2)关联于f(1)2(x,y),等。
步骤5 将该位平面进行扩散及排序,每一块的扩散方法如图2所示,排序方法由该点所处位置与步骤4所述相关联的混沌值来决定,该混沌值处于式 (4)中的哪一个集合,就对该点采用步骤2中所述该集合所相关联的方法来排序。直到整个位平面上的点都进行移位为止。
步骤6 生成本轮置乱所用混沌序列值之后的连续4个混沌值,重复步骤3到步骤5的过程直到加密者设定的迭代次数。
该算法相应解密过程是加密过程的逆过程,同样需要定义集合与引入混沌序列元素,这里就不再详细讲述。
2 安全性分析
一个加密算法的好坏主要是从其一些性能上得以分析,本节给出一些对出几个关于图像加密算法的优劣的评定方法,对本文给出的改进算法的性能进行讨论。
2.1 密钥空间分析
所谓密钥空间就是指所有可以被用做各个密钥来进行加/解密的数字的空间。一个好的加密算法,其为了保证有足够的抗强行攻击的能力,其密钥空间一定要足够大。
分析本文所给出的算法的密钥空间,可以看出其包含两个方面的密钥:①位平面排序过程中所采用的两个混沌序列的初始值和参数。②对各层位平面进行置乱处理时采用的混沌序列的初始值和参数。若按照文献 [1]中所述方法在位平面排序过程中采用Chebyshev map.来生成混沌序列,分别控制对行和列进行排序,参照式 (2),两个混沌序列则需要两个初始值x0和y0,以及两个参数k和v 来进行控制,其4个值均为浮点型。同时,在对排序后各位平面进行置乱操作中,分别对各层使用不同参数与初始值的Logistic序列。参照式 (1),每一个Logistic序列包括μ 和初始值x0两个参数来控制生成。8个位平面则包含8*2个浮点型数字可以来作为密钥。同时根据需要,每一个混沌序列生成后从哪一位开始选取也可以作为一个整形密钥来,每一个位平面进行置乱处理时的迭代次数也是可以作为一个整形密钥来辅助使用,以加强整体加密算法的抗攻击能力。相比较于文献 [1]中对各平面采用猫脸
变换时为整形密钥,本文所给出算法具有更强密钥空间,因此具有更强抵抗攻击能力。
2.2 统计分析
在上一章的分析中已经提到,为了能够抗统计分析攻击,一个好的加密算法必须具有足够的鲁棒性来面对各种形式的基于统计理论的攻击方法。本节我们将从直方图,相邻像素相关性以及信息熵3个方面对本文所给算法的抵抗统计分析攻击的能力进行分析。
在接下来的实验中,我们分别将基于混沌序列的位平面排序时使用的两个Chebyshev映射的初始值和参数分别标记为x0和y0以及k和v,同时将排序操作后的8个位平面在置乱处理时分别采用的8个Logistic映射的初始值和参数分别记为x10,x20,x30,x40,x50,x60,x70,x80以及μ1,μ2,μ3,μ4,μ5,μ6,μ7,μ8。(最低一位的平面对应x10和μ1,第二低位的平面对应使用x20和μ2,以此类推)。最后将位平面置乱时的统一迭代次数记为M。
基于以上分析,我们按照表1~表3中的参数使用本文所给加密算法对原始图像进行加密。

表1 Logistic映射的初始值

表2 Logistics映射的参数

表3 Chebyshev映射初始值和参数
2.2.1 直方图
对于灰度图像,直方图就是该图像中所有像素点的像素值的一个统计量。攻击者可以通过对加密图像的直方图进行统计分析的方式获取明文图像的相关信息,因此,一个好的加密算法必须使得加密图像的直方图相比原始图像的直方图发生较大的改变。
在使用表1~表3中参数进行直方图实验仿真结果如图3所示。
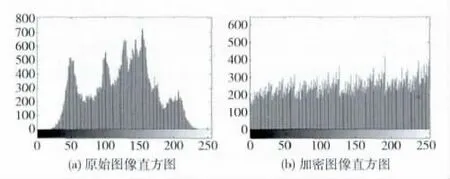
图3 直方图分析
图3的实验结果表明,在采用本文所给出的加密算法后加密图像的直方图较加密前有了较大的改变,仅从加密后的图像中很难获取原始图像的有用信息,而且加密后的图像的直方图相比于待加密图像的直方图更加接近于均匀分布,无法从加密后图像当中获取任何有效的统计信息。综上所述,本加密算法具有较好的抗统计分析的安全性能。
2.2.2 相邻像素相关性
由于所有的图像都携带有视觉内容,其相邻像素的灰度值一定存在很高的相关性,这种相邻包括水平相邻,垂直相邻以及对称轴相邻。在对图像的这一项属性进行定量分析的时候,往往使用式 (5)
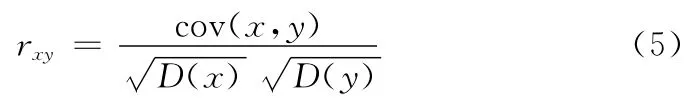
通过式 (5),我们随机选取1000组相邻点进行计算分析可以得到加密前后图像相邻像素值的相关系数见表4。

表4 相邻像素相关系数
以下我们用统计图像来分别展示原始图像和加密图像的相邻像素值的相关性,这里只选取垂直相邻像素来做以展示,如图4所示。

图4 垂直相邻像素相关性
通过以上实验所得数据和图像可见,本文所给出加密算法能够较好地改变原始图像相邻像素间的相关性,因此在此方面具有较好的加密效果。
2.2.3 信息熵
在信息论中,信息熵被用来作为一个极其重要的属性来描述信息的不可预见性。为了方便统计信息熵,常使用以式 (6)

式中:si——每一个可能的取值,P(si)——可能取si的概率,N——可能取值的总数。经过计算后得到原始图像及加密图像的信息熵见表5。

表5 原始图像及加密图像信息熵
对于本实验中采用的灰度值为256 的原始图像,其最理想的信息熵的值应该为8,使用本文给出加密算法所得到的信息熵很接近最理想值。可见本算法具有较强的抵抗信息熵攻击的能力。
2.3 密钥敏感性
一个好的加密算法应该对密钥有良好的敏感性,具体说来,其表现为,当解密密钥即使非常接近于正确加密密钥时,解密图像也与原始图像具有很大的差别,以确保该算法具有抗暴力攻击的能力。为了对本文所给出的加密算法的密钥敏感性做以评估,在对排序后的8个位平面采用表1~表3中所示数据分别加密后,我们将每一个位平面上某一个密钥做微小改动 (其它的不变)进行错误解密 (具体数据改动见表6),然后将错误解密位平面与对应的排序后位平面进行异或运算,最后统计其不相同点的比例,结果见表7。

表6 错误密钥值

表7 错误解密相差比例
如表7中可以看出,对于每一个位平面,只要在解置乱过程中某一密钥发生微小改变,错误解密位平面将会与原始位平面各点的值发生较大差错,通过对两个不相关二值图像进行同样分析可发现差错50%已属于不相关,因此该位平面置乱方法具有较好的密钥敏感性。
2.4 抗剪切攻击
由于本文所给出加密算法中的位平面置乱环节的基本思想是将各位平面分块后穿插组合再多次迭代,使得本来相邻很远的点有机会变为邻近点,同时把相邻的点分散开来,这样就使得加密后的图像具有一定的抗剪切攻击的能力。
为了验证本文所给出加密算法的抗剪切能力,以下实验模拟加密后图像被非法获取者剪切攻击,在合法获取者得到剪切后的加密图像后用正确的密钥解密图像。实验结果如图5所示。

图5 剪切14%以后的恢复效果
通过实验结果可以看出,图5为加密图像被攻击者进行剪切攻击掉一定比例后用正确密钥解密所得图像,所得图像具有较好的恢复效果,实验结果表明本加密算法具有较好的抗剪切攻击能力。
3 结束语
本文给出一种改进的图像加密算法。参照文献 [1]中加密算法基于位平面加密的主体思路及结构,作为改进,将其对位平面的处理时采用了一种改进的置乱算法,该种图像置乱算法与传统的猫脸变换等算法相比较,在密钥空间方面具有较大改进,同时具有一定的抗剪切攻击能力。由实验结果可以看出,本文所给出加密算法具有较好像素置换效果,加密后的图像较原始图像直方图有了较大改变。另一方面本算法具有较大的密钥空间,并且对密钥具有较强的敏感性。同时由于加密算法中采用改进的像素置乱算法所具有的扩散穿插作用,使得算法具有了一定的抗剪切攻击的能力。
[1]Fu C,Lin B,Miao Y,et al.A novel chaos-based bit-level permutation scheme for digital image encryption [J].Optics Communications,2011,284 (23):5415-5423.
[2]LI Chuanmu,HONG Lianxi,WAN Chun.An image blocking encryption arithmetic based on chaotic sequences [J].Computer Technology and Development,2007,17 (8):51-54 (in Chinese).[李传目,洪联系,万春.基于混沌序列的图像分块加密方法[J].计算机技术与发展,2007,17 (8):51-54.]
[3]YANG Xue,YU Xiaoyang,ZOU Qifeng,et al.Uniform block encryption algorithm of image based on affine modular transformation [J].Journal of Nanjing University of Science&Technology:Natural Science Edition,2010,34 (4):441-447 (in Chinese).[杨雪,于晓洋,邹奇峰,等.基于仿射模变换的图像分块均匀加密算法 [J].南京理工大学学报:自然科学版,2010,34 (4):441-447.]
[4]REN Hong'e,SHANG Zhenwei,ZHANG Jian.Image encryption algorithm based on chaotic map [J].Computer Engineering and Applications,2009,44 (31):202-204 (in Chinese).[任洪娥,尚振伟,张健.基于混沌映射的图像加密算法 [J].计算机工程与应用,2009,44 (31):202-204.]
[5]SUN Jinguang,WANG Jie,JIANG Wentao,et al.Application of improved blocking algorithm in rectangle image encryption [J].The Research and Application of Computer,2013,30 (1):282-284 (in Chinese). [孙 劲 光,汪 洁,姜 文 涛,等.改进的分块算法在矩形图像加密中的应用 [J].计算机应用研究,2013,30 (1):282-284.]
[6]TIAN Yan,XIE Yubo,LI Tao,et al.An image scrambling method based on image blocking and chaos system [J].Journal of Image and Graphics,2007,12 (1):56-60 (in Chinese).[田岩,谢玉波,李涛,等.一种基于分块和混沌网的图像置乱方法 [J].中国图象图形学报,2007,12 (1):56-60.]
[7]YUAN Suiwei,FAN Jiulun.Image encryption algorithm based on permutation transformation [J].Journal of Xi’an University of Post and Telecom,2010,15 (3):60-67 (in Chinese).[袁岁维,范九伦.一种基于排序变换的图像加密算法 [J].西安邮电学院学报,2010,15 (3):60-67.]
[8]Indrakanti S P,Avadhani P S.Permutation based image encryption technique[J].International Journal of Computer Applications,2011,28 (8):45-47.
[9]Fateri S,Enayatifar R.A new method for image encryption via standard rules of CA and logistic map function [J].International Journal of Physical Sciences,2011,6 (12):2921-2926.
[10]Li S,Li C,Lo K,et al.Cryptanalyzing an encryption scheme based on blind source separation [J].IEEE Transactions on Circuits and Systems,2008,55 (4):1055-1063.
[11]Patidar V,Pareek N K,Sud K K.A new substitution-diffusion based image cipher using chaotic standard and logistic maps[J].Communications in Nonlinear Science and Numerical Simulation,2009,14 (7):3056-3075.
