曲面的有限元网格顶点法矢算法

阳湘安，阮 锋

（1.广东技术师范学院 机电学院，广东 广州510635；2.华南理工大学 机械与汽车工程学院，广东 广州510640）

0 引 言

在薄板的有限元成形过程仿真中，经常采用四边形网格或三角形网格或两者的混合网格对模型进行曲面的离散化。其中，离散网格顶点法矢对于计算顶点曲率、网格光顺、网格优化和网格变形以及离散网格的曲面拟合等都具有重要的作用［1－3］，对于有限元的计算结果也有一定的影响。

计算离散网格顶点法矢的主要方法目前可以区分为2类，即基于二次误差矩阵法向表决的法矢计算方法和权重平均的法矢计算方法。第1类计算方法精度较高，但是计算的法矢仍然依赖于某权重，同时，对于两面偏差角大于或等于90°时，需要调整算法，甚至得不到结果，而且通过测地线来计算顶点的邻域也很耗时［4，5］。对于曲面的离散网格顶点的法矢计算，更多的是采用第2类计算方法［6－8］，考虑到网格的不规则性，也有提出计及质心位置坐标的权重方法或者单独引入网格的形状因子来计算权重［9，10］，但是，对于曲面的有限元网格划分，由于有限元计算的要求，曲面划分后的离散网格的形状通常是较为规整的，因此，需要正确评估这种情况下各种权重平均的法矢计算方法的计算精度和效率，同时，目前针对三角形网格的顶点法矢算法比较成熟，但关于四边形网格、四边形网格与三角形网格并存的混合网格的顶点法矢计算的研究则较少，基于这种情况本文提出了解决这一问题的算法。

1 三角形离散网格曲面的法矢计算

1.1 基于二次误差矩阵法向表决的法矢计算方法

这种方法的思想首先是确定顶点的邻域，即一系列的三角形网格平面fi，则点x 到三角形网格平面的距离为

式中：p——三角形网格平面上的某个点，δi＝－为三角形网格平面到原点之间的距离，——三角形网格平面的法矢。

而带权重wi的n 个通过同一个点p 的平面与x 的距离的平方为

这里采用权重wi是考虑各三角形网格平面的贡献差异，而采用距离的平方则考虑到对方程求最小值后得到二次误差矩阵方程，对于所求网格顶点，其与1－ring三角形网格平面的距离为0。式 （2）最小化后得到如下方程

一般来说，A 是对称、半正定的，假设求得其特征值为λi（λ1≥λ2≥λ3），对应的特征向量为，则其中的特征向量即为要求取的顶点法矢。

1.2 权重平均的法矢计算方法

基于二次误差矩阵法向表决的法矢计算方法需要较大的工程计算量，相比来说，权重平均的法矢计算方法则简便得多，然而，很多确定权重的方法都是基于经验来进行的，只对某类曲面的网格有较高精度。典型的权重确定方法有：

（1）等权重方法，即各三角形网格的权重相等且一般都取为1，因而，网格顶点法矢的计算为

（2）面积权重法。这种方法认为三角形网格的面积对顶点法矢的影响是主要的，因而以各三角形网格的面积Ai作为各自法矢的权重，网格顶点法矢的计算则为

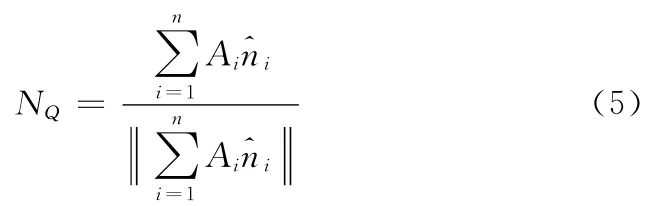
（3）角度权重法。这种方法则认为顶点相邻两边的夹角对顶点法矢的影响具有最大影响，因而根据顶点相邻两边的夹角αi大小来确定权重，网格顶点法矢的计算为

（4）角度和面积乘积的权重法。在这一方法中，权重的确定综合考虑了角度和面积的影响，其表达式为

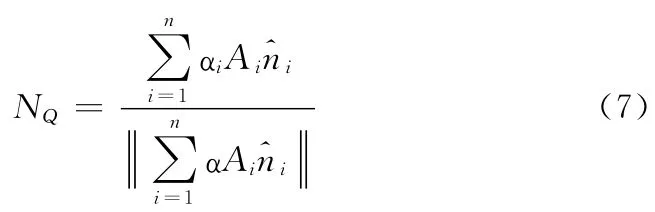
（5）质心位置的权重确定方法。这种方法认为质心的位置能够比较全面地反映三角形网格的形状。为了考虑三角形网格形状对权重确定的影响，权重的确定采用如下表达式

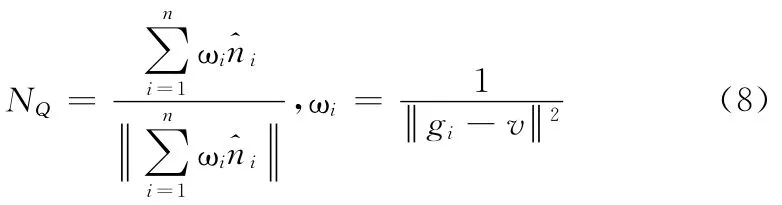
式中：ωi——质心权重，gi——三角形网格的质心位置。

1.3 Max方法的原理

1.2节中各种权重平均的法矢计算方法都是根据经验来确定的，缺乏相应的理论依据，而Max算法虽然形式上体现为一种通过权重平均来确定网格的顶点法矢，但本质上来说是一种通过外接球面拟合四面体来确定顶点法矢的方法，因而具有相应的理论依据。

图1所示，对于以Q 为顶点、Vi为节点的三角形网格系列，选取其中的2 个三角形网格QV1V2和QV2V3，则点Q、V1、V2和V3构成一个四面体，而通过四面体的4个顶点可以做出唯一的一个外接球面，于是，通过三角形网格边线QV1、QV2、QV3的中点A、B、C可以构建其相应的3个法平面方程，对3个方程的联立求解则可以得到球面圆心O 的坐标，而矢量O→Q 则为由这2个相邻三角形网格确定的法矢。

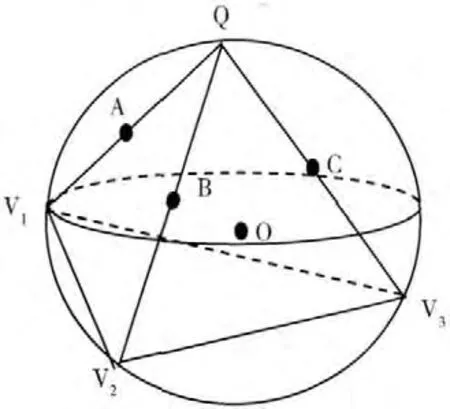
图1 Max算法原理

对网格顶点及其邻接n个三角形网格循环采用上述方法并将结果归一化，则得到最终的网格顶点法矢

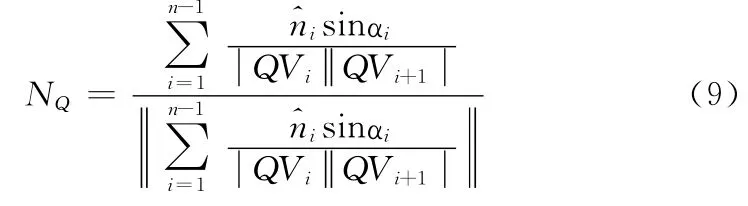
2 有限元网格顶点的法矢算法

2.1 典型曲面样本的有限元网格模型

为了比较各种权重平均的法矢计算方法的结果精度，选取以下4种曲面为对象，通过有限元网格划分后得到四边形网格模型或者同时带有四边形网格和三角形网格的混合网格模型。划分后的网格模型如图2所示。

图2 典型曲面样本有限元网格模型

在上述曲面的有限元网格模型中，半球面和圆锥面大部分为四边形网格，但在边界处出现三角形网格，这种情况在实际中最为常见，而环面和圆柱面则由于比较规整，因而划分出的网格只有四边形网格。由于实际中三角形网格的顶点法矢计算较为成熟，因而，可以采取将四边形网格转化为三角形网格的顶点法矢计算模式。

2.2 有限元网格顶点法矢的算法流程

将四边形网格转化为三角形网格的方法有很多种，典型的有3种，如图3所示。方案 （a）中，对于四边形网格中的某节点Vij，将Vij与Vi－1，j－1和Vi＋1，j＋1连接 起来 即 产生新的边，这样四边形网格就分解成了三角形网格；方案（b）中，对四边形网格中的满足i＋j为偶数的点Vij，将点Vij与其1－邻域中的对角点连接，产生的线段作为加入的新边，这样也形成了三角形网格；方案 （c）中，则直接对矩形域上的所有顶点作Delaunay三角剖分［11］。

图3 四边形网格到三角形网格转换的典型方法

对于网格顶点法矢的计算来说，应该尽量利用顶点周围邻近节点的信息，而上述方案都没有满足这一要求，并且，由于物理上并不需要将四边形网格划分为三角形网格，因而，对于所需求取法矢的网格顶点，可以首先搜寻到与其直接相邻的其他网格顶点，将其中属于同一个四边形网格单元的网格顶点连接起来，从而与所需求取法矢的网格顶点一起构成计算所需的三角形网格。如对于顶点Vij，将与其直接相邻的节点Vi，j＋1、Vi－1，j、Vi，j－1和Vi＋1，j依次连接起来构成四条新边，进而与顶点Vij共同构成计算其顶点法矢的三角形网格，如图4所示。

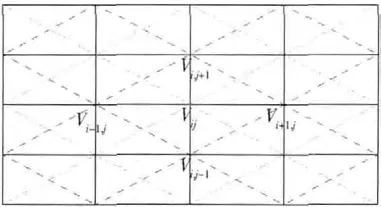
图4 四边形网格到三角形网格的处理

编程计算流程为首先将四边形网格转换为三角形网格模式，再针对三角形网格采用不同的权重平均算法来计算，具体流程如图5所示。

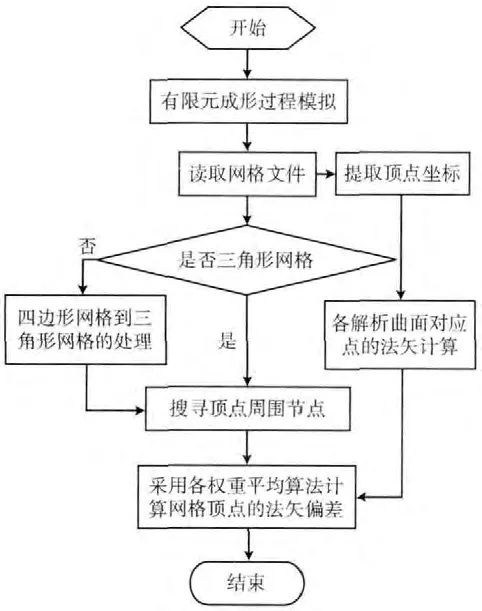
图5 有限元网格顶点法矢的算法流程

采用各种权重平均的法矢计算方法对上述曲面样本网格模型分别进行编程，计算各顶点的法矢，得到的结果见表1。

各类型曲面网格顶点法矢计算结果的最小均方根偏差和最小绝对值平均偏差对应的计算方法见表2。

3 结果分析

从表1和表2可以看出，对于半球面、环面和圆柱面，Max方法相对于其他权重平均方法来说，其计算结果的均方根偏差和绝对值平均偏差都最小，对于圆锥面来说，其计算结果的绝对值平均偏差也最小，而均方根偏差为0.0046 mm，相对于其他权重平均方法的最小值0.0042 mm 来说，差距也并不是很大。

这说明，Max 方法不但计算精度很高，而且具有很强的适应性。这主要是因为Max方法在计算顶点法矢时对于两相邻的三角形网格构成的四面体采用外接球面进行拟合，精确计算出2个三角形网格时顶点的法矢，并循环采用这一方法计算出其它两相邻三角形网格时的顶点法矢，由于这种方法在计算时同时考虑了两个相邻三角形网格的法矢，因此，当将所有结果作矢量加得到最终顶点的法矢后，其结果精度必然就会很高；而且，由于对两相邻的三角形网格构成的四面体采用外接球面进行拟合，因而也必然计及了三角形网格的形状规整性，这一结论从文献［10］中也可以看出。从计算效率来说，由于Max方法最终可以推导为如式 （9）所示的简单形式，因而其算法的效率也不会很低。相对而言，其它的权重方法只是考虑如何对一个单独的三角形网格确定权重，而且其权重的确定也主要是从经验的角度来考虑，没有相应的理论依据，因而其结果精度不但较低，而且对于不同类型的曲面其结果精度不稳定。

表1 各方法的偏差比较

表2 最小偏差对应的计算方法

从表1和表2还可以看到，采用等权重法计算后结果的均方根偏差和绝对值平均偏差也都比较小，其中对于圆锥面来说，其均方根偏差和绝对值平均偏差都最小，对于半球面，其均方根偏差也最小。究其原因，主要是由于有限元计算的要求，通常划分后的网格都比较规整，而其它的经验性权重平均方法中引入的权重因子由于并不能全面反映三角形网格的形状差异，因而这些方法并不能有效提高计算结果的精度。由于等权重的计算简单，又具备一定的计算结果精度，因而，对于有限元网格顶点的法矢计算要求不是非常高的情况下，从计算效率的角度考虑是可以采用的。

4 结束语

文中首先阐述了计算三角形网格顶点法矢的各种方法的原理和特点，针对典型曲面的有限元网格的顶点法矢计算，分析了基于经验的权重平均法与Max方法的计算结果精度。结果表明，对于计算结果精度要求较高且计算效率要求也较高的情况，可以采用等权重法来确定曲面有限元网格的顶点法矢，而对于计算结果精度要求很高的情况，则应该采用基于外接球面拟合四面体的Max 方法达到这一目标。

文中针对四边形网格以及四边形和三角形网格并存的情况，提出了将四边形网格处理为三角形网格并有效计算出网格顶点法矢的方法，这一方法尽量考虑到了利用网格顶点相邻节点的的信息；设计的算法不但可以单独处理四边形网格或三角形网格，而且能够处理曲面有限元网格划分后四边形网格和三角形网格混合并存的情况。

［1］HE Qiang，ZHANG Shusheng，BAI Xiaoliang.Mesh smoothing algorithm based on local surface approximation ［J］.Journal of Harbin Institute of Technology，2011，43 （5）：89－93（in Chinese）.［贺强，张树生，白晓亮.基于局部曲面逼近的网格光顺算法 ［J］.哈尔滨工业大学学报，2011，43 （5）：89－93.］

［2］CHEN Zhiyang，HAN Chunlei.Simplification and reconstruction of mesh model in CAE ［J］.Computer Systems ＆Applications，2011，20 （5）：188－191 （in Chinese）. ［陈志杨，韩春雷.面向CAE的网格模型特征简化与重建 ［J］.计算机系统应用，2011，20 （5）：188－191.］

［3］ZHANG Aiwu.Surface reconstruction with normal control［D］.Jinan：Shandong University，2009 （in Chinese）.［张爱武.法矢控制的网格曲面重建若干问题研究 ［D］.济南：山东大学，2009.］

［4］Di Angelo L，Di Stefano P.Experimental comparison of methods for differential geometric properties evaluation in triangular meshes［J］.Computer－Aided Design and Applications，2011，8 （2）：193－210.

［5］Hyun Soo Kim，Han Kyun Choi，Kwan H Lee.Feature detection of triangular meshes based on tensor voting theory ［J］.Computer－Aided Design，2009，41 （1）：47－58.

［6］YANG Nan，XIAO Jiangchao，WANG Minghai.Estimation of normal and curvature based on the triangle mesh model［J］.Modern Manufacturing Engineering，2010，38 （3）：104－107 （in Chinese）.［杨楠，校江超，王明海.基于三角网格模型的法矢及曲率估算［J］.现代制造工程，2010，38 （3）：104－107.］

［7］Kim Hyoung－Seok，Kim Ho－Sook.New computation of normal vector and curvature ［J］.Wseas Transactions on Computers，2009，8 （10）：1661－1670.

［8］ZHANG Yajuan，LI Ze’an，CHENG Chen.Modified smoot－hing algorithm of triangular mesh model［J］.Computer Engineering，2012，38 （9）：220－222 （in Chinese）. ［章雅娟，李泽安，程晨.一种改进的三角网格模型光顺算法 ［J］.计算机工程，2012，38 （9）：220－222.］

［9］Chen Yueping，Gao Jian，Wen Hao，et al.Estimation normal vector of triangular mesh vertex by angle and centroid weights and its application ［J］.TELKOMNIKA，2013，11 （4）：1841－1848.

［10］PENG Yuhui，GAO Chenghui.An improved algorithm for vertex normal computation of triangular meshes based on shape correction ［J］.Journal of Image and Graphics，2010，15（1）：142－148 （in Chinese）.［彭育辉，高诚辉.基于形状修正的三角网格模型顶点法矢估算方法 ［J］.中国图象图形学报，2010，15 （1）：142－148.］

［11］WANG Cheng’en，CUI Dongliang，YAN Zhiyuan，et al.Finite element triangle mesh generation in planar area ［J］.Computer Integrated Manufacturing Systems，2011，17 （2）：256－260 （in Chinese）.［王成恩，崔东亮，严智远，等.平面区域有限元三角形网格划分研究及实现 ［J］.计算机集成制造系统，2011，17 （2）：256－260.］