提离式基础抗震性能研究综述

董 凯

（同济大学 土木工程学院,中国 上海200092）

0 引言

震是困扰人类的一大自然灾害，就近年来说，最近30余年，地球上发生了多次地震灾害。2008年5月12日发生在我国四川的“汶川”8.0级特大地震，造成了巨大的人员伤亡和经济损失。桥梁工程作为震后重要的交通枢纽，对于营救伤员、发放救援物资具有重要作用。而桥梁由于其特殊性，往往又是线路上的薄弱环节，在地震作用时易产生破坏。其中基础的破坏较为常见。过去，扩大基础为了地震时能够承受较大的地震力，往往将尺寸设计得过大，高度过厚；桩基础中，桩或桩中主筋往往深入承台，地震时地面运动通过桩-承台固结体系，将能量传至上部结构，上部结构过大的惯性力反过来又可能导致桩上拔及剪切破坏。为此，地震时，如果允许扩大基础底面与土体短暂分离（或桩与承台分离），这样传至上部结构的地震能量会大大减小。同时，由于基础（或承台）与下面交替提离与接触，这样会来回摇摆，延长结构自振周期，从而避开了场地的卓越周期，进而减小了整个桥梁的地震反应。各国学者从上世纪六十年代以来，投入大量精力进行研究，以期给桥梁抗震带来新的设计思路。本文从理论研究、试验研究和工程应用三个方面来进行简要叙述。

1 理论研究

二十世纪六十年代，有地震工程师（Housner1963；Meek 1978）指出了结构摇摆减震机制的应用前景.。在大地震的震害调查中发现，有一些很脆弱的结构由于不经意的摇摆而在地震中安然无恙（Cloud 1963；Hanson 1973）。Housner(1968)被认为是第一个明确地将基础提离与结构的地震反应联系起来的科学家。Clough和Huckelbridge(19771978)根据三层钢框架式房屋模型的振动台试验也证明，允许柱基产生提离可改善结构的性状，使其破坏大大减轻，也就是说允许基础出现提离，可以降低对于框架的强度和延性要求。Muto等（1980）通过单自由度结构模型的振动台试验和计算分析，发现柔性结构在其基座上做摇摆运动，在地震时是十分稳定的。经过几十年的发展，研究者已经提出了几种模型来模拟提离的发生，常用的模型有以下三种：

1.1 Housner刚体摇摆理论

Housner[1]首先观察到地震中建筑物的摇摆并对这种现象进行分析。在他的一本书中,分析了块体的自由振动并建立了数学方程来计算摇摆周期及由于振动而产生能量损失。Housner的摇摆块模型如图1所示。

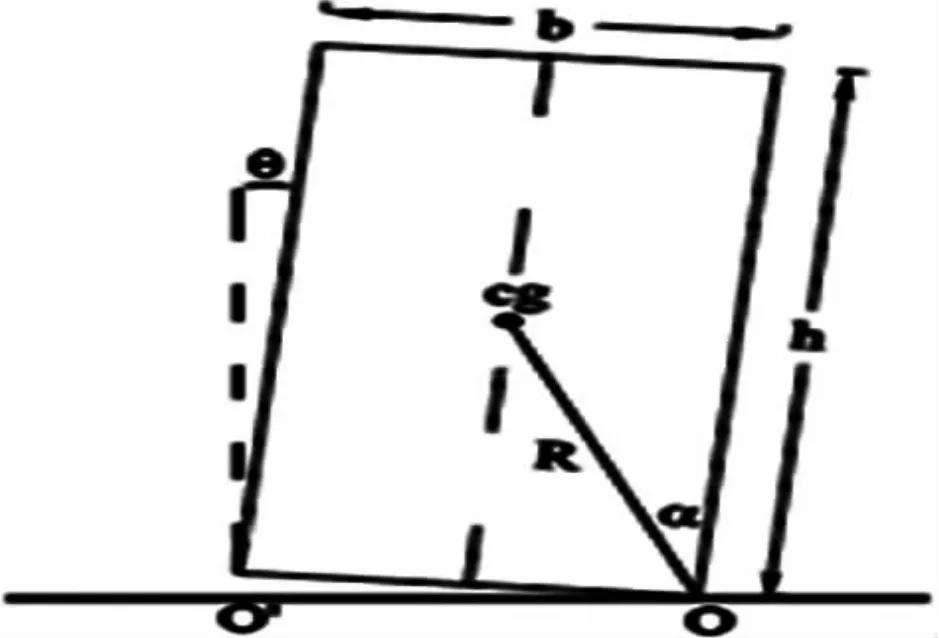
图1 Housner刚性摇摆模

1.2 采用Winkler弹簧模型扩大基础的提离

和复杂的有限元及边界元模型相比，Winkler弹簧模型在模拟土-结构相互作用时更为简便。Winkler模型更便于实际应用。Allotey通过研究Winkler模型，推导出可以应用于土-结构相互作用的状态方程并成功地求解了基于Winkler模型的刚性基础的弯矩-转角响应问题。基于Winkler弹簧模型，提离基础共有6种不同的响应状态，分别是：先弹性后提离、弹性与提离同时发生、先提离后弹性、先屈服后提离、先提离后屈服及达到弹塑性极限。

1.3 改进的Winkler弹簧模型

美国联邦应急管理局推荐了几种不同的方式来使用Winkler弹簧。他们推荐采用竖向刚度和旋转刚度非耦合的模型[2]。如图2所示，有两种不同的弹簧：中弹簧和边弹簧。边弹簧单位长度的刚度是基于L×B/6的基础竖向刚度；中弹簧单位长度的刚度等于无限长基础的竖向刚度。

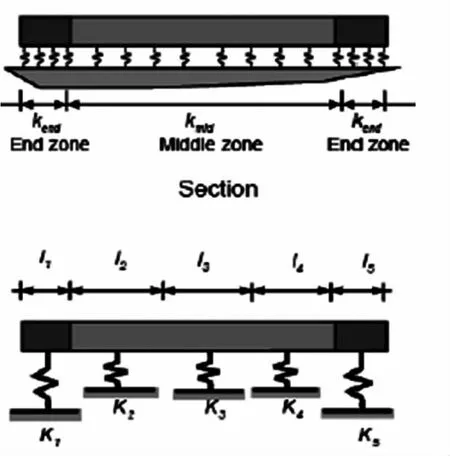
图2 Winkler弹簧模型

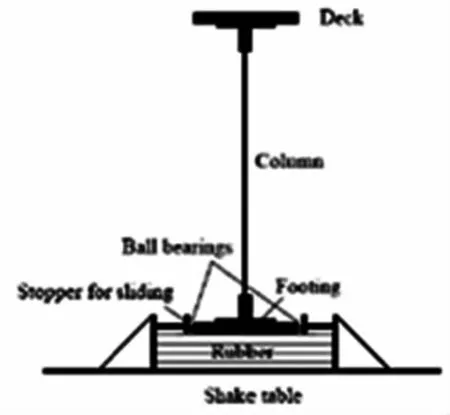
图3 Sakellaraki的试验模型

2 试验研究

试验研究主要分为两种类型，一种重点是研究基础和土体相互作用，此时基础与土体接触面会产生永久变形；另一种是主要研究提离对上部的影响[3]。下面就这两类试验分别选取一个典型例子进行说明。

2.1 Sakellaraki试验

Sakellaraki[4]进行了一次小型提离式基础的振动台试验。他通过使用缩尺模型模拟了基础-桥墩-主梁系统，这个系统包括桥面板、立柱、桥墩、基础以及土体。试验构件高度是840mm，基础截面宽度是300mm，他所采用的构件如图3。考虑了主梁两侧质量、墩柱刚度、基础大小及地面刚度。振动台试验考虑了五条地震波，包括Kobe1995、Turkey1999和 Ojiya2004。

2.2 Espinoza和Mahin试验

Espinoza和Mahin[5]采用大比例尺模型来分析桥墩的提离效应。这些桥墩承受多向地震荷载。虽然这仅仅是个初步的试验，但很多结果值得一提。经过简化将钢筋混凝土墩柱及基础模型放在50mm厚的橡胶垫上。墩柱直径为410mm，选择的基础宽度是3倍的墩柱直径，构件总高度为275cm，构件如图4所示。采用各级地震单向及双向加载。然后各级地震加载均保持墩柱为弹性。

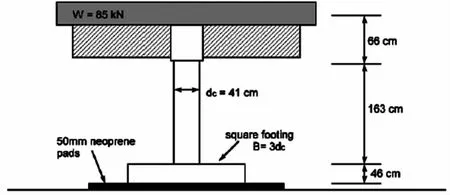
图4 Espinozo的试验模型

图5 Rion-Antirion桥加筋土隔震基础

3 工程应用

近几十年中，已有一些实际桥梁采用提离式基础的概念，主要有新西兰的 Honshu-Shikoku 桥、Akashi Straight桥、Kurushima Straight桥以及希腊的Rion-Antirion桥。希腊的Rion-Antirion桥采用新型的基础形式--加筋土隔震基础，我们可以看到提离式基础的概念，从下面的介绍中，可以看出此种基础形式混合了提离式桩基础和扩大基础的特点。

Rion-Antirion横跨希腊科林斯海峡，主桥为多塔结合梁斜拉桥，桥面连续，采用五跨全漂浮结构体系。该桥桥位的建设条件非常复杂，要求大桥能够承受2000年一遇的地震，最大峰值加速度达到1.2g。桥梁要承受巨大的地震力，而此处海床20m深范围的土层力学性能不好。主桥桥塔基础最终构造如图5所示，采用了直径达90m的圆形钢筋混凝土箱筏基础。为提高土的性能，用长25～30m的钢管以7～8m的间距进行土体加固，每墩下约有250根钢管桩。为允许基础和地基之间的滑动，在钢管上铺设厚50cm的反虑砂层，其上铺设厚2m、直径为10～80cm的鹅卵石层，最上面铺设厚50cm的碎石层。这样桥梁基础直接摆放在上述总厚3m的砂砾层上，基础和砂砾层连接较弱，可在地震时产生向上及左右的移动（但在运营期及小地震时不会滑动），起到了隔震的作用。[6]

4 总结

本文从提离式基础的理论研究、试验研究和工程应用三个方面进行叙述，简要回顾了这种新型基础形式近几十年来的发展状况。提离式基础由于能够通过土体塑形耗能和摇摆减隔震来减小上部结构在地震时所承受的加速度，由此会很大程度的降低桥梁整体由于抗震设计而增加的费用。相信在不远的将来，提离式基础能够成为一种地震区常采用的基础形式。必须说明的是，我们国家在这个方面起步晚，和世界先进水平（如新西兰）相比，有较大差距。希望通过本文的简要叙述，引起工程技术人员的重视并为他们提供一些参考。

［1］Housner G W．The Behavior of Inverted Pendulum Stuctures during Earthquake[A]//Housner G W．Bulletin of the Seismological Society of America，Vol．53，No．2，pp．403-417．

［2］FEMA 356．Prestandard and Commentary for Seismic Rehabilitation of Buildings[Z]．Washington，D．C：Fedral Emergency Management Agency，2000．

［3］王立忠．提离式桩基础抗震性能拟静力试验研究[D]．上海：同济大学，2010．

［4］Sakellaraki，D．and Kawashima，K．Effectiveness of Seismic Rocking Isolation of Bridge Based on Shake Table Test[A]//Sakellaraki．First European Conference on Earthquake．

［5］Espinoza A．and Mahin S．Rocking of Bridge Piers Subjected to Multi-Directional Earthquake Loading[A]//Espinoza．Technical Memorandum of Public Works Research Institute，No.4009，pp．65-71．

［6］Espinoza A．and Mahin S．Rocking of Bridge Piers Subjected to Multi-Directional Earthquake Loading[A]//Espinoza．Technical Memorandum of Public Works Research Institute，No．4009，pp．65-71．