应力知识在热水瓶防爆上的应用
2014-12-23吴月勇曹明纬朱文旺
吴月勇 曹明纬 朱文旺
(1.河海大学 港口航道与近海工程学院,江苏 南京 210098;2.河海大学 土木与交通学院,江苏 南京 210098)
我们平时在使用保温瓶接开水时,时常都有水瓶内胆玻璃突然爆炸碎裂的现象,且这种现象在冬季尤为严重;今年入冬,身边就又多起水瓶爆炸的现象。而且令人担心的是许多保温瓶内胆玻璃破碎是无法预计的,如地震、玻璃自爆。撞击等。这些情形下,现在的保温瓶可能大多没有任何形式的防护,这样危险的不确定性就更大了。之前有一些人对开水瓶做过改进,他们大多采用以下两种方式:一是采用金属材料制作保开水瓶,金属瓶胆虽然坚固耐用,不易损坏,但导热率远大于玻璃,制成的瓶胆保温效能较差,且较普通开水瓶重;二是用塑料制成的单层或双层壁容器,填充泡沫塑料隔热,轻巧方便,不易破碎,但其保温效能比真空瓶胆差。
为了克服服现有技术中的不足,提供一种带有防爆膜的防爆热水瓶。它与传统开水瓶最大的不同是在水瓶内胆外覆有防爆膜。使其在不增加水瓶重量的条件下起到防爆或者减小爆炸伤害的作用。
所述防爆膜为条状PET 膜,防爆膜的粘贴角度与内胆径向轴线的夹角为40~50 度,防爆膜许可宽度为内胆内径的2~4 倍。所述防爆膜防爆膜的粘贴角度与内胆径向轴线的夹角为45 度,防爆膜许可宽度为内胆内径的3.14 倍。有益效果:本实用新型的有益效果是在不明显增加开水瓶重量,保证开水瓶保温效果的基础上,提高开水瓶内胆防爆性能,且结构简单,易于推广。
附图说明:
图1 是本防爆热水瓶的正面半剖视图。
图2 是本防爆热水瓶的内胆计算模型图。
图3、4、5、6、7 是本防爆热水瓶的计算简图
具体实施方式:
如图1 所示的一种防爆开水瓶,包括有内胆1,所述内胆1 外覆有条状PET 膜作为防爆膜2,防爆膜2 的粘贴角度与内胆1 径向轴线的夹角为45 度,防爆膜2 许可宽度为内胆1 内径的3.14 倍。
如图2 所示,设内胆1 内直径为D,内胆1 厚度δ 远小于内胆1内直径D,将内胆1 简化为一圆柱形压力容器,将防爆膜2 粘贴其上,防爆膜2 与内胆1 横截面夹角为θ,防爆膜2 的宽度为b。容器内蒸汽压为P,防爆膜2 能承受的最大应力为W,那么由圆筒受力对称性可知,圆筒横截面处各点的正应力σ1 相等。
如图3、图4 所示,设F 代表力,圆筒横截面上的正应力σ2=F/A=P*(πD^2)/4=(PD)/(4δ)由于δ 远远小于D,故计算中圆筒横截面积A=π Dδ。
如图5 所示,为计算圆筒纵截面上的正应力σ1,假想地截取一段单位长的圆筒,沿纵截面将其切开,并研究其上半部分。由于圆筒上下部分的对称性,所以,纵截面上没有切应力,对于δ 远小于D 的薄壁圆筒,可以认为纵截面上个点的σ2 相等,而该段圆筒内表面上压力的合力Fp=PD,于是由上半部分圆筒的平衡方程∑Fy=0,PD-2,σ1*δ*1=0,即得σ1=PD/(2δ)(y 是下标,即∑Fy=0 来表示径向压力的合力为0),容器内表面上任一点处沿直径方向的正应力为σ3=-P,于是,可得圆筒内表面上各点的应力分别为σ1=PD/(2δ)、σ2=(PD)/(4δ)、σ3=-P,由于D/(4δ) 远大于1,即σ3 得绝对值远远小于σ1 和σ2,故可以视σ3=0,如图6 所示,可得圆筒各点处于平面应力状态。
上述中σ1、σ2、σ3 均需小于W所述防爆膜2 呈条状,宽度(即许可宽度)为b,如图7 可得防爆膜2 的粘贴接缝方位角θ(“防爆膜2 与内胆1 横截面夹角θ”与本方位角θ 为同一角)的正弦、余弦分别为sinθ=b/(∏D),cosθ=√((∏D)**2-b**2)/(∏D),防爆膜2 接缝处拉应力σθ 应满足的条件为σθ=σ1*sinθ**2+σ2*cos**2<=σ1 即防爆膜2 条内最大拉力,将σ1、σ2、sinθ、cosθ 代入式中得b<=(∏D)=3.14D,所以防爆膜2 的许可宽度b 为内胆1 内径的3.14 倍。
由第三强度理论可得最危险点位于圆球部分,可以在圆球部分适当增加防爆膜2 的厚度,为了安全可为其它部分的两倍。
如附图6,最大切应力作用面为附图六中的阴影面,其与σ2 与σ1 各成45 度,所以θ 取45 度最安全。

图1
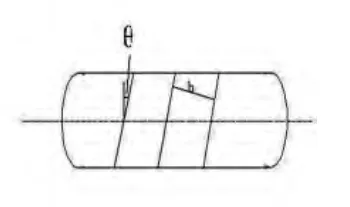
图2

图3
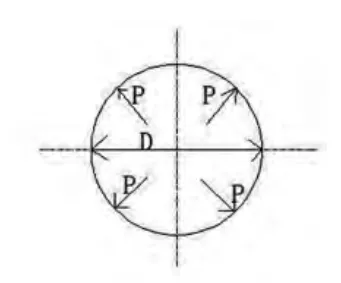
图4
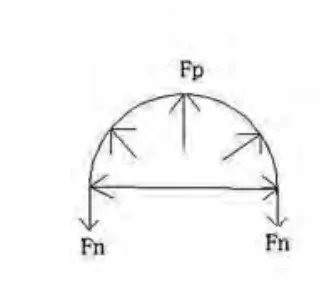
图5

图6
[1]孙训方,方孝淑,关泰来.材料力学[M].北京:高等教育出版社,2009,7.
[2]王非.压力容器设计应力分析[M].北京:化学工业出版社,2011,1.
