行业电量中的相关性分析及其在电力营销中的应用

2014-12-23庞建军夏振超张雪莲

科技视界 2014年31期

关键词：供电量回归方程电量

庞建军夏振超张雪莲

（广州供电局有限公司萝岗供电局，广东广州 510400）

0 引言

电量预测[1-3]是供电企业开展电力营销[4-5]的基础性工作。现有的电量预测模型，往往仅考察历史电量数据自身的特点，而对数据形成背后的影响因素缺乏深入的分析，这样预测得到的结果可信度其实有待商榷。

电量变化受多种因素影响，若能计算出各影响因素对电量变化的具体影响程度，则可以对电量预测结果进行修正，并可以挖掘出影响电量变化的关键因素，从而明确电力营销工作重点。

影响电量变化的因素有很多，可分为外部因素和内部因素。外部因素中的某些因素，如人口、气候、经济等都有一定的数据记录，可进行相关性分析，而另外一些因素，如能源政策、环保标准、科学技术水平等通常是通过语言来表述，没有量化数据，难以直接分析其对电量的影响。不过，这些因素的影响往往可以通过某些经济指标的变化反映出来，因此可以通过对经济指标与电量做相关性分析，间接地反映这些因素对于电量的综合影响。

每个行业的电量可以看做是影响电量变化的内部因素。一个地区的总电量是由若干个不同行业的电量组成的，不同行业的发展情况不同，电量变化规律也不相同，通过对行业电量和总电量进行相关性分析，就可以知道哪些行业是影响总电量变化的重要因素[6]。

本文拟引入相关性分析[7]方法，利用简单相关系数[8]和复相关系数来考察电量与单因素及多因素之间的相关程度，从而找出影响电量变化的关键因素，为做好电力营销工作提供重要依据。

1 相关性分析方法

研究各种不确定因素（如人口、气候、经济等）对电量预测的影响程度，需要对它们进行相关性分析。常用的相关性分析方法是计算变量之间的相关系数。相关系数可分为线性相关系数和非线性相关系数[7-8]。线性相关系数又分为简单相关系数和复相关系数。本文只研究线性相关系数。

1.1 简单相关系数

简单相关系数（简称相关系数）是反映两变量间线性相关关系的统计指标。设n 维向量X 与Y，则X、Y 的相关系数为：

相关系数ρXY取值在-1 到1 之间，ρXY=0 时，称X，Y 不相关；ρXY＞0，表示正相关；ρXY＜0，表示负相关。ρXY的绝对值越大，表示变量X、Y 的线性相关程度越高；ρXY的绝对值越小，则变量X、Y 的线性相关程度越低。|ρXY|=1 时，称X，Y 完全相关，此时，X，Y 之间具有线性函数关系。|ρXY|＞0.8 时称为高度相关，当|ρXY|＜0.3 时称为低度相关，其余为中度相关。

1.2 复相关系数

复相关系数是反映一个变量与其他多个变量之间线性相关程度的指标。复相关系数无法直接求出，需要先求出多元线性回归方程。

设n 维向量Y 与其他m 个n 维向量X1，X2，…，Xm，则Y 与X1，X2，…，Xm之间的复相关系数计算过程如下：

（1）求Y 与X1，X2，…，Xm的多元线性回归方程，得：

（2）Y 与X1，X2，…，Xm的复相关系数为：

可发现，简单相关系数其实就是复相关系数m=1 时的一个特例，计算简单相关系数的时候也可以先求出X 与Y 的一元线性回归方程。由于多个变量的变化趋势很难保持一致，复相关系数的正负就失去了意义，因此一般只看复相关系数的绝对值，|ρ|越大，表明变量Y 与X1，X2，…，Xm之间的线性相关程度越密切。

2 行业电量中的相关性分析

由上文的分析可知，影响电量变化的因素有外部因素和内部因素，可量化因素和不可量化因素。行业电量就是影响总电量变化的内部因素，尤其是一些支柱行业、朝阳行业具有重要的分析价值。行业电量中的相关性分析，应当筛选出可进行分析的和具有分析价值的影响因素，并设计合适的相关性分析方法，从而全面考察电量与各影响因素之间的关系。

2.1 行业分类依据

供电企业统计的电量数据一般是按照电价类别和国家标准《国民经济行业分类》来对用电行业进行分类。按照电价标准的不同可以将用电用户分为大宗工业用户、非工业普通工业用户、商业用户、居民用户、农业用户、稻田排灌用户。《国民经济行业分类》将用电行业分为若干门类、大类、中类和小类，共有4 个层次，分类的细致程度逐层加深。实际应用时可根据需要进行灵活合理的分类。

2.2 对行业电量进行相关性分析

2.2.1 影响因素的筛选

外部因素中可进行分析的有经济、人口、气象数据，其中经济指标有GDP、工业增加值、进出口总额等，人口指标有户籍人口、常住人口、流动人口等，气象指标有年平均气温、月平均气温、月最高（低）气温等。内部因素中可进行分析的为各行业的历史电量值。

具有分析价值的影响因素有：常住人口、月平均气温、GDP、工业增加值、进出口总额、地区支柱行业的电量值。

2.2.2 行业电量的相关性分析方法设计

（1）单因素相关性分析

计算总电量与单个因素之间的简单相关系数，验证两变量的线性相关程度。

（2）多因素相关性分析

计算总电量与多个因素之间的复相关系数，验证总电量与多因素之间的线性相关程度。

3 算例分析

以某供电局（以下以L 局代替）为例，进行相关性分析。由于人口和气象数据缺乏，外部因素只选取了GDP、工业增加值和进出口总额。而内部因素选取了大工业用户中的汽车、电子、食品药品、金属加工、轻工日化五个支柱行业。

（1）单因素相关性分析

分别计算L 局总供电量与当地GDP、工业增加值和进出口总额的相关系数，结果如表1 所示。为了更直观的反映总共电量与各因素之间的相关程度，也求出了各组的一元线性回归方程。其中L 局季度供电量与当地GDP 的散点图及一元回归曲线如图1 所示。

表1 单因素相关性分析结果

图1 L 局季度供电量与当地GDP 的散点图及一元回归曲线

由表1 可见，L 局总供电量与三项经济指标之间都呈正相关的关系，且简单相关系数值都在0.8 以上，说明L 局总供电量与三项经济指标分别具有较高的线性相关程度。由图1 可见，原始数据的散点散落在一元回归曲线附近，直观的显示出L 局总共电量与当地GDP 较高的线性相关程度。

（2）多因素相关性分析

分别计算L 局总供电量与GDP、工业增加值、进出口总额之间、L局总供电量与五大行业供电量之间、L 局大工业供电量与五大行业供电量之间的多元线性回归方程和复相关系数，计算结果如表2 所示。

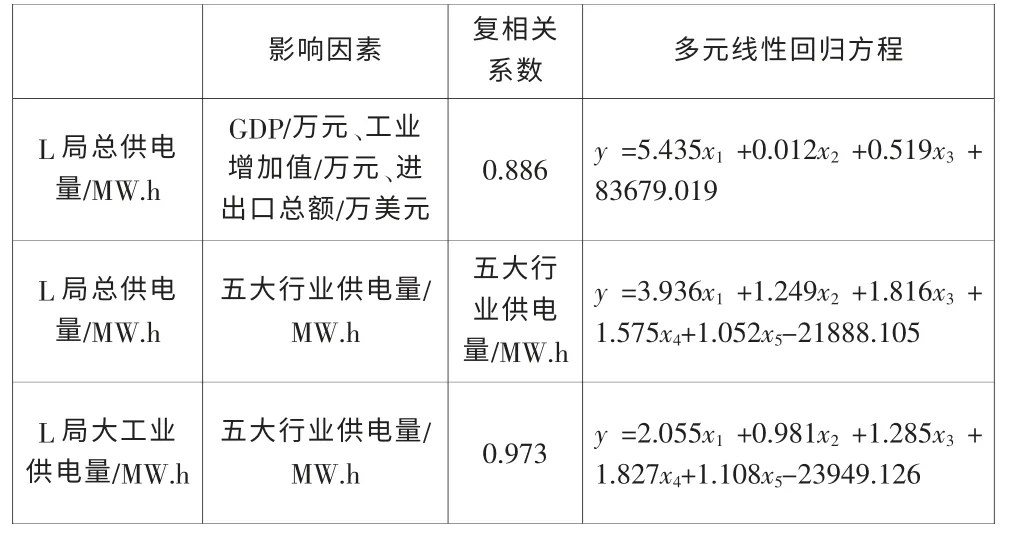
表2 多因素相关性分析计算结果

由表2 可见，3 组多因素相关性分析得到的复相关系数都在0.8以上，属于高度相关。L 局总供电量与五大行业供电量之间、L 局大工业供电量与五大行业供电量之间的复相关系数都达到了0.95 以上，表明这五个行业作为支柱行业，对于L 局总供电量和L 局大工业供电量的带动作用都是很明显的，应作为做点关注对象。

综上，该算例中选取的影响因素都是与L 局总供电量相关程度很高的因素，应作为电力营销工作关注的重点。参照这些影响因素的变化趋势，可以对电量变化趋势进行一定的估计。甚至在政府经济相关部门对GDP、工业增加值、进出口总额等经济指标作出预测的基础上，结合表2 中的多元线性回归方程，可直接预测出L 局的总供电量。