基于多分辨率小波变换的砂岩累积疲劳损伤识别
2014-12-21吴振祥樊秀峰简文彬
吴振祥,樊秀峰,简文彬
(1.福州大学环境与资源学院,福建福州350108;2.福州大学岩土工程与工程地质研究所,福建 福州350108)
岩石的声波信号是岩石中各种裂隙与损伤产生的反射、折射等多种波相互叠加的结果,也是岩石内部微观结构的综合表现。声波信号中包含复杂的频谱成分,但目前对于岩石中各种裂隙的声波信号生成机理还无法给出理论上的描述,声波信号中各成分波的时频特性未知,使得对声波信号的精细分析受到相当大的限制[1-3]。
目前小波在岩土工程领域得到广泛应用[4-8],近几年用在岩石等材料损伤检测方面的研究也日益增多[9-12]。有些学者曾尝试把小波变换用于混凝土损伤及岩石破裂过程的研究,对混凝土结构损伤进行在线监测,确定损伤位置[11];也有基于小波变换时频能量分析技术进行岩石声发射信号的时延估计,以确定损伤[12];赵明阶[1]应用小波变换理论对岩石在加载及卸载过程中的声波信号进行分解,提出了对应力敏感变化的波谱参数。在循环荷载下岩石的损伤与单独的加、卸载过程不同,呈现循环累进的特点,微裂纹从萌生、发展到形成经历了一个累积发展过程。如何能有效跟踪损伤的发生、发展,进行累积疲劳损伤的精细识别,对于揭示损伤的声学机理,评价岩石(体)结构完整性具有重要的意义。
本文针对循环荷载作用下砂岩的累积疲劳损伤问题,利用Fourier变换(FFT)进行声波信号频域分析的同时,引入小波变换理论,运用小波变换的多分辨率理论对声波信号进行分解,获得不同频带的信号分量,对各频带分量进行独立分析,从声波分析信号中提取出反映循环荷载条件下岩石疲劳损伤程度的敏感波谱参数。
1 砂岩疲劳损伤的声波测试
本次试验在疲劳加载的同时,同步进行超声波速的测量,设计超声波传感器固定在试件上,在加载过程中可以连续、实时测量超声波的变化。试验砂岩采自福建三明沙县,为中风化,岩石试件呈灰黄色,块状结构。试件尺寸为50 mm×50 mm×100 mm的长方体,测试过程如图1所示[13]。

图1 试验系统原理图
2 声波信号的快速Fourier频谱分析
对岩石声波信号进行快速FFT变换,对信号的频率结构进行分析。
2.1 快速Fourier变换(FFT)的基本原理
信号X(t)的快速Fourier变换为:

它表示一个声波波形X(t)可分解为数个不同频率、不同振幅、不同相位的正弦波的叠加。
2.2 砂岩疲劳损伤过程的FFT变换结果
为了研究疲劳损伤过程中岩石试件超声波信号的频域变化规律,对循环加载试验中所测得的声波记录进行FFT频谱分析,其中选取典型试件的分析结果如图2所示。
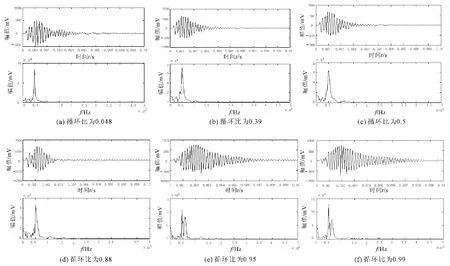
图2 典型试件不同循环比下超声波信号波形及其频谱图
图2中显示砂岩试件在经历了不同次数的循环荷载后从波形图上几乎看不出明显的变化。观察其相应的频谱图,在循环次数比从0.048到0.5的过程中,频域的幅值发生衰减,试件频谱主要以单峰形式出现,内部损伤表现不明显;循环次数比达到0.88以后,频谱形态开始由单峰向双峰转变,预示着宏观的微裂纹已经快形成,在整个损伤过程中主频率的变化不敏感。
通过对多个试件进行FFT变换后的主频及最大频域幅值进行统计分析,得到其随疲劳循环次数比的变化规律曲线如图3、图4所示。

图3 典型试件主频随循环次数的变化规律曲线

图4 典型试件最大频域幅值随循环次数的变化规律曲线
图3、图4曲线显示,在整个循环加载过程中,试件的主频呈现有规律的波动,总体趋于稳定;试件的频域幅值在整个疲劳过程中出现较大幅度的波动,无明显规律,到临近破坏时出现急剧下降。
前述可知,利用传统的FFT方法得到的频谱特性参数(主频、频域幅值)在疲劳损伤过程中随损伤的变化不敏感。岩石试件未出现宏观裂缝前,对于微裂纹的萌生、扩展,响应信号频谱变化规律性不明显,只有当试件彻底开裂后(宏观裂纹已经形成),信号频谱才发生明显的下降。因此,利用FFT方法只能对破坏发生时的宏观裂纹作出明显响应,而对微小损伤不敏感。
3 基于小波变换的砂岩疲劳损伤超声波信号的损伤识别
由于岩石的超声波信号是一种复杂的、带有噪声的非平稳随机信号,其频谱是时变函数,传统的FFT方法对频率的分辨率较低,且分辨率不可调,使计算结果敏感程度大幅度降低,多种噪声信号干扰,无法精细地识别出有用的特征信号。
小波多分辨率分析继承并发展了FFT方法,使频率成分在时域或频域上均可调,并可逐步精细化,有效抓住信号的瞬变、奇异等细节,可以很好地反映岩石节理、裂纹等萌生、扩展的损伤程度[14]。
3.1 超声波信号的多分辨率小波变换理论
多分辨率分析是小波变换的精髓之一,根据Mallat提出的小波变换的多分辨率分析理论[14-15],将信号f(x)分解成不同的频带:
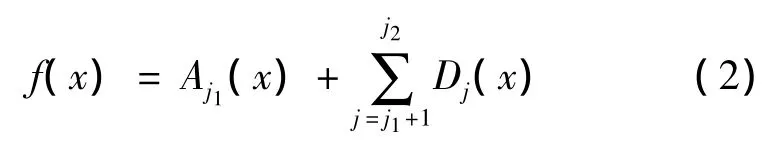
其中系数由递推公式经C0推出:
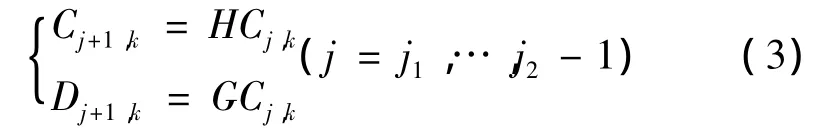
其中φ(x)为尺度函数,ψ(x)为小波基函数,低通滤波器H和高通滤波器G均由φ(x)和ψ(x)决定。
3.2 砂岩疲劳损伤过程中超声波信号的小波变换
3.2.1 小波基函数的选择
在工程应用中,用于变换的小波基函数有多种,最优小波基的选取是重要的环节,选择的正交小波基应满足一定的平滑性、紧支集和对称性[16]。岩石声波信号小波基选择方法,首先,查找与超声子波形状相近、衰减较快的波形作为初选;其次,对原始信号和小波变换后的重构信号进行误差比较,择优选定。经过几个小波函数的比较,最后选用 Daubechies小波对响应信号进行正交小波变换。
3.2.2 砂岩损伤过程中超声波信号的小波变换结果
采用Daubechies5小波对疲劳损伤过程中的超声波信号进行了4尺度的小波分解,选择上述典型试件进行分析说明,其小波分解变换结果如图5所示。
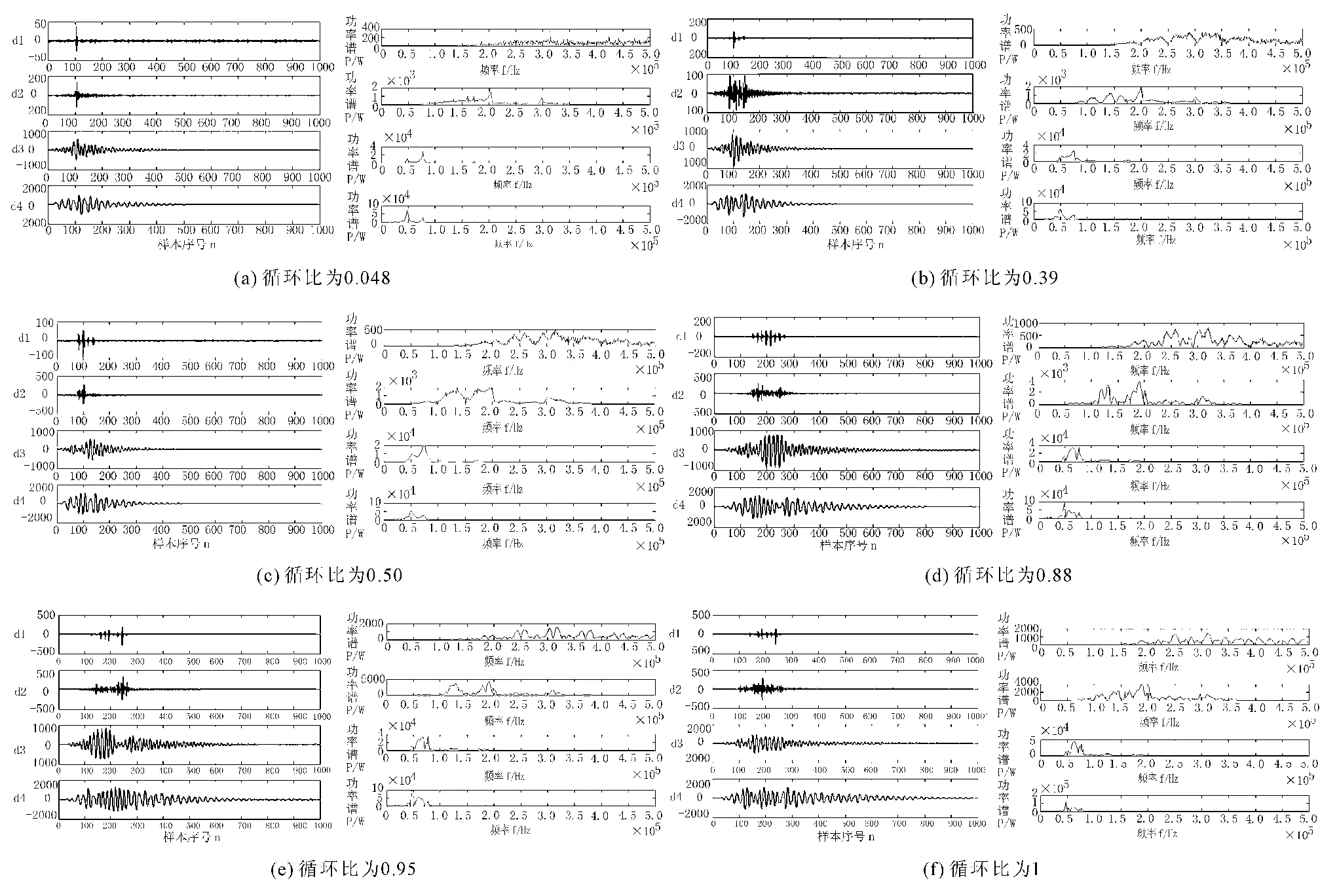
图5 典型试件的超声波信号4层小波分解及相应的频谱分析
图5显示,损伤过程中裂纹的萌生与发展对超声波信号的低频段影响不太显著,而对高频段的影响比较显著。从小波系数重构的时域图(尺度分析图)可以看出低频段(d3、d4重构段)在整个循环过程中幅值及波形的变化很小,对损伤的识别不够敏感;而在高频段(d2、d1重构段)在整个循环过程中幅值及波形都发生了显著的变化,当岩石试件出现微小裂缝时,在小波尺度信号的高频部分相应出现了一些峰值(如图5(c)开始),对损伤过程比较敏感。从超声波信号尺度对应的频谱分析中可以看出,d1、d2段的频谱曲线幅值及频率成分在循环加载过程中随着裂纹的萌生与发展呈现有规律的变化。
对声波信号经小波变换后不同频带再进行Fourier变换,处理后得出主频率(f0在频谱曲线中最大振幅对应的频率),频域最大振幅(Afmax),谱面积(M0,振幅谱曲线对频率的积分,它表征了声波传播所携带的能量)等参数随应力循环比的变化曲线,如图6所示。图6中显示不同尺度上主频率、频域幅值及谱面积随循环应力比均表现出较强的规律性,但不同尺度变化的敏感程度不同,其中第一尺度(d1)由于其中含有较高的噪声污染,不重点考虑;第二尺度(d2)的频域参数值随循环应力比的变化最为敏感(见图6(a)、图6(b))。
主频率在不同损伤阶段发生较为明显的变化,随循环次数比的增大呈逐渐衰减的趋势,表现出高频向低频漂移的渐进过程,表明岩石试件损伤不断加大的同时,穿过损伤的超声波主频率在不断的衰减。由于FFT变换对整个时域进行分析,因而在不同频带上的频率变化相互干扰,并且还有高频噪声的污染,真正的频率变化特征被其它频带所掩盖,所以只通过FFT变换无法精细地识辨频率的变化。
对于频谱幅值及谱面积随损伤过程的变化,在第一阶段中,由于试件的初始损伤程度不同,内部结构及成分的差异比较大,所以这阶段不同岩石试件的频谱幅值及谱面积的变化差异性比较大;进入第二阶段,频谱幅值及谱面积在不同频率段(不同尺度条件)下敏感性不同,总体呈现出一定的上升趋势;到第三阶段,频谱幅值及谱面积参数发生突然下降,伴随着裂纹的贯通,高频成分大幅度衰减。

图6 超声波信号小波变换各尺度主频、频域幅值、谱面积随循环次数比变化曲线
4 超声波敏感损伤参数的加权识别
对声波信号进行小波分解后,略去在第一尺度下的小波分量(即高频干扰),对其余尺度下小波分量的波谱参数进行自身加权平均,获得加权波谱参数:
波谱参数加权

由于加权波谱参数是超声波在各个频带上的能量或主频率的加权平均,因此在物理意义上,它仍然是超声波在各个频带上的频率或能量的一种综合特征,并且实现对损伤敏感的频带上的信号更加突出。
把上述公式用于图6中各参数进行计算,可得如图7所示试件的加权波谱参数随疲劳循环次数之间的关系,由图7可以看出,通过小波变换得到的加权波谱参数比由FFT变换得出的波谱参数对疲劳损伤过程具有更强的敏感性。
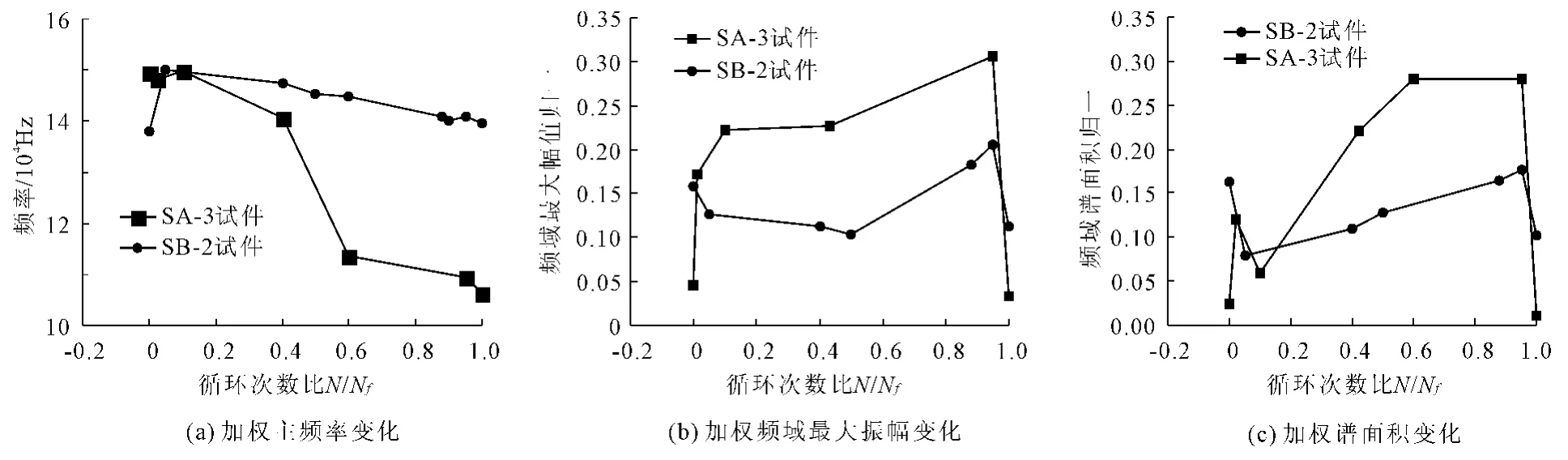
图7 超声波信号小波变换各尺度加权波谱参数随循环次数比变化曲线
5 结论
(1)岩石在疲劳损伤过程中,应用FFT方法进行超声波信号的频域参数分析表明,疲劳损伤过程中砂岩频谱图的形状从单峰向多峰转移,但是主频率随循环次数比的变化并不敏感,只有出现宏观裂纹以后,才发生明显的下降。
(2)引入小波的多分辨率分析技术,实现声波信号在不同尺度下的精细分析,并进行加权处理后发现,主频率随损伤过程呈现一个渐进性的衰减变化,频域最大幅值及谱面积也随循环次数的增加表现出较强三阶段规律性。
(3)加权波谱参数,是超声波在各个频带上的能量或频率的综合反映,同时也使对损伤敏感频带上的信号更加突出;波谱参数的敏感变化为下一步损伤识别的理论模型研究奠定基础。
[1]赵明阶,吴德伦.小波变换理论及其在岩石声学特性研究中的应用[J].岩土工程学报,1998,20(6):47-51.
[2]Zhu Xing,Xu Qiang,Zhou Jianbin,et al.Experimental study of infrasonic signal generation during rock fracture under uniaxial compression[J].International Journal of Rock Mechanics & Mining Sciences,2013,(60):37-46.
[3]俞 缙,赵维炳,苏天明,等.岩石超声波信号的小波时频分析[J].地下空间与工程学报,2008,3(6):1094-1098.
[4]宋 健,高广运.近断层速度脉冲地震动对边坡滑移的影响分析[J].岩石力学与工程学报,2014,33(2):317-326.
[5]Jung-Doung Yu,Myeong-Ho Bae,In-Mo Lee,et al.Nongrouted ratio evaluation of rock bolts by reflection of guided ultrasonic waves[J].Journal of Geotechnical and Geoenvironmental Engineering,2013,139(2):298-307.
[6]杨红伟,许 江,吴 鑫,等.周期水压力作用下砂岩变形试验与小波分析[J].重庆大学学报:自然科学版,2011,34(4):6-12.
[7]徐安权,徐卫亚,石 崇.基于小波变换的数字图像技术在堆积体模拟中的应用[J],岩石力学与工程学报,2011,30(5):1007-1015.
[8]梁桂兰,徐卫亚,谈小龙,等.岩石高边坡安全监测数据的小波变换去噪处理[J].岩石力学与工程学报,2008,27(9):1837-1844.
[9]Lee I M,Han S I,Kim H J,et al.Evaluation of rock bolt integrity using Fourier and wavelet transforms[J].Tunnelling and Underground Space Technology,2012,28(1):304-314.
[10]Ma Rui,Zhang Tianjun,Qiao Baoming.Application study on of wavelet analysis during compression ruptrue procedure of coal sample[C]//Advanced Materials Research,2013,616-618:2182-2186.
[11]李洪泉,董 亮,吕西林.基于小波变换的结构损伤识别与试验分析[J].土木工程学报,2003,36(5):52-57.
[12]康玉梅,朱万成,白 泉,等.基于小波变换时频能量分析技术的岩石声发射信号时延估计[J].岩石力学与工程学报,2010,29(5):1010-1016.
[13]樊秀峰,简文彬.砂岩疲劳特性的超声波速法试验研究[J].岩石力学与工程学报,2008,27(3):557-563.
[14]Mallat S G.A theory for multiresolution signal decomposition:the wavelet representation[J].Pattern Analysis and Machine Intelligence,IEEE Trans.,1989,11(7):674-693.
[15]胡昌华,张军波,夏 军,等.基于Matlab的系统分析与设计——小波分析[M].西安:西安电子科技大学出版社,2000.
[16]苗玉杰.岩石声发射信号处理小波基选择的探讨[J].计算机光盘软件与应用,2013,16(6):15-17.
