交通荷载特性及其模拟方法研究

田 飞，褚进晶

(扬州大学 建筑科学与工程学院，江苏 扬州225009)

1 前言

交通荷载，主要是指车辆在道路上行驶所产生的荷载。车辆本身是一个多质点振动系统，当车辆在路面上行驶时，由于路面不平整，对于直接与路面接触的车轮而言，它是以一定的振幅和频率在路面上跳动前进的，从而导致作用在路面上的车辆荷载时而大于静载轮载，时而小于静载轮载。此外，车辆行驶于路面时，车轮对路面某一固定点的作用时间非常短，大约 0.01 s～0.1 s，在路面以下一定深度持续的时间虽然略长，但仍然十分短暂。因此，车辆荷载对路基的作用时间长短与汽车行驶速度直接相关，随着车速的增加，路基承受荷载的时间会成比例的减少。尽管对于路基上某一点，车辆荷载的作用时间非常短，但在公路的整个设计寿命中，累加起来的时间也是很长的，因此，交通荷载对路基的作用有荷载累计作用时间长，次数多的特点。

国内的现行道路设计方法中，仍大多将汽车荷载简化为静力荷载，将行车荷载假设为常量[1－2]，这在以前道路和交通量都未得到充分发展的情况下，有一定的参考意义，但随着道路以及交通工具的发展，车辆轴载越来越大，超重车辆的出现也越来越普遍。由美国州际公路工作者协会(AASHO)在1958年—1961年从事大规模试验时得出的四次幂理论表明，静态轴载与路面损坏的关系在车速较慢，轴载较轻的道路上偏差不大，但在车速快或者超重载作用于弱路面时则有较大偏差[3]。为方便计算，很多学者将车辆荷载均换算成等效土柱[4－5]以简化计算，这种计算方法暴露出了静态恒载计算方法的不足，即当交通量增大时，换算的等效填土高度与实际荷载差值非常明显。徐毅[6]认为造成这种差别的原因主要是由于没有考虑到车辆荷载的动力作用，未进行动荷载的等效计算。日本建设省在 Arikae粘土上进行的低路堤交通载荷试验[7]表明，车辆跑动时在土中产生的竖向附加应力为车辆静止时的三倍，虽然有设计者将静载乘以冲击系数做为设计轮载，但这种处理方式仍然是基于静力上的等效，无法表现车辆动态的变化过程，有很大的局限性。

将汽车荷载简化为静力荷载进行设计，得出的结论不符合实际道路的运行情况，实际车辆荷载是一个很复杂的动荷载问题，同时涉及到很多方面，包括车辆本身的因素:如轴重、悬挂体系、行车速度等;以及道路的因素如基层或路面组成、路面的平顺度等[8]。因此，对交通荷载的特性进行研究，并找出一个较好的模拟方法，对道路设计具有非常重要的意义。因此，很多学者利用垂直荷载乘以相应的系数来综合考虑车辆产生的动荷载，从而达到简化荷载的效果。黄永强[10]通过研究发现，在所有影响随机车辆荷载的因素中，路面不平整度是最关键的因素，而其他因素与之相比，影响非常微弱。这是因为路面不平度会激励行驶车辆使之产生振动，这种振动会导致车辆对路面产生附加动荷载，并以一定频率施加给路面结构。

以往交通荷载的模拟方式，按照其作用方式，大致分为三种，即:恒载作用、移动恒载作用、振动移动荷载作用。

(1)恒载作用

恒载作用是假设汽车荷载为静止的均布荷载或者集中荷载，其大小为车辆本身的自重，示意图如图1所示，表达式如式(1):

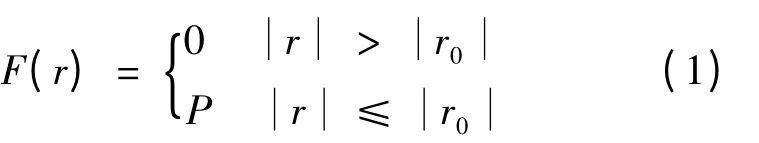
式中:r0为车辆荷载分布的边界至荷载中心距离;P为均布荷载均值。

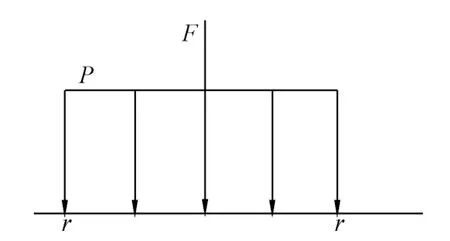
图1 车辆荷载静载模型

2 交通荷载的模拟

本文主要在列举了交通荷载的各项特点的基础上，结合扬州地区的一条典型道路上的相关交通量及其各个层次的材料参数，拟合出了交通荷载的作用公式，并利用有限元软件Abaqus分别进行二维和三维情况下的模拟，并就模拟出的压力－时间变化图、动位移－时间变化图以及交通荷载影响深度等进行分析，结果显示，采用带参数的正弦公式模拟交通荷载是比较合理的。

2.1 交通荷载的特点

要对交通荷载特性进行分析，首先要对车辆荷载进行分析。车辆荷载主要是由汽车产生的各项荷载通过其车轮传递给路面，从而对道路产生的各项作用力:包括水平力和竖向力。其中水平力会在车辆加速和减速中呈现动态变化，具体表现为:车辆加速时，水平力为与行进方向相反的摩擦力，车辆减速时，对路面产生与行进方向相同的摩擦力。车辆动荷载是一种随机性荷载，它与车型、车速、车辆行驶中的固有频率、路面不平整度、路面材料、车辆载重量等诸多因素有关。因此，车辆荷载的运动和大小都是随机变化的。李伟等[9]通过研究发现，车辆对路面产生的水平力的变化，对车辆对路面产生的总体动荷载的影响不大，或者说，车辆速度的变化，对车辆对道路产生的垂直应力、横向应力及车轮边缘下方的竖直剪应力等荷载的影响很小。

静态恒载模型考虑了荷载分布形式的不同，当r0很小时，F(r)就会变成集中荷载。如果荷载线性分布，那么2r0就是线源分布长度;如果荷载面状分布，那么r0就是分布的半径。对于静载，一般通过《公路沥青路面设计规范》中规定来取值。对于垂直荷载，一般采用双轮组单轴轴载100 kN(即标准轴载BZZ－100)作为P，对于因车辆类型的不同对道路结构的损坏作用产生的差别，则通过不同轴载等效换算的标准当量作用次数来反映。

(2)移动恒载作用

移动荷载作用则是将恒定的车辆荷载沿着行驶方向移动，这种方式虽然模拟了车辆动态的性质，但其荷载值和静态恒载一样，是定值，无法反映车辆荷载在行驶中产生荷载的变化，由此出发所作的相关研究，虽然较恒定荷载已有很大的进步，但仍然有很大的局限性，并随着道路建设水平以及交通工具的发展，越来越不能满足工程实际需要。

(3)振动移动荷载

振动移动荷载是以一定的振动幅值、频率的周期性动载来模拟交通荷载。这种模拟方式能较好的反映车辆动荷载特性，并可以通过改变振动规律的方式进行不同交通量以及不同轴载车辆荷载的模拟。

2.2 交通荷载大小的确定

目前常见的振动荷载拟合方式大致可分为两类:即稳态正弦波振动和随机振动两种形式，随机振动荷载是最接近实际情况的动荷载，但是，由于路面不平整本身就是随机的，而加上车辆、车型、车速以及实际行驶荷载的随机性，导致了这种荷载模拟方式的各种变化都有瞬态随机性，只有借助统计学，对各种不同的情况进行实际测定、分类以及统计等一系列繁琐的工作，才可能建立相关的模型，这种方式需要消耗大量的计算资源，并需要大量数据支持，且建立的模型往往适用性很有限，很难得出有实际应用价值的结论。随着道路的发展，路面平整度问题已经得到了很大的改善，因此在平整度好的路面上行驶的车辆，一般随机性不是很大，其对路面产生的荷载变化一般都有较好的规律性，可以把车辆荷载的变化近似的看作呈周期性函数变化。对此，国内外学者一般都采用稳态正弦波振动来模拟汽车荷载。在考虑了车辆速度、轴重、路面平顺性、面层刚度、面层平整度、基层强度等一系列因素的情况下，采用如下[11－12]表达式:

式中:P0为车轮轴重，代表车辆荷载中的静载部分;相应的，Pd则代表车辆荷载的动载部分。对于P0的取值，目前采用较多的是按照规范中车辆轮载进行相应的换算。若以小汽车为研究对象，一般取为20 kN，而对于大型汽车，则取为100 kN。对于 Pd的具体取值，各个学者的意见仍存在很大的争议，归结起来，是因为车辆类型、悬挂软硬程度，车速等等有很大的随机性。

本文对扬州市华扬西路的交通情况进行了调查，认为该路段虽然地处绕城高速，但由于沿途学校较多，车辆行驶限速为80 km/h。通过对早上8点至晚上6点之间10 h内通过的2 126辆汽车车速的测定，得出该路段通过车辆的平均车速为72 km/h，利用凌建明[13]提出的行车速度与加载时间关系式:

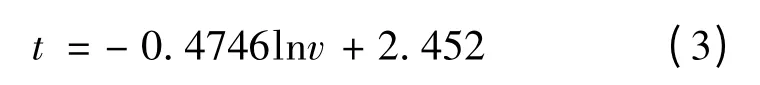
根据上式得出，车辆在路面的加载时间约为t=0.4 s，调查中，路过此地的2 126 辆车中，1 903 辆为小型客车，因此，本文取小客车为研究对象。关于交通荷载中动荷载Pd的模拟方法，目前的研究中一般采用车辆簧下质量Mo、路面几何不平顺矢高α，以及车辆假设的振动频率ω三项系数合成来计算的。不考虑行车间距的影响，本文计算中采用的计算公式为:

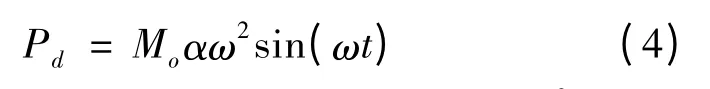
其中:Mo取为小客车车辆簧下质量120 N·s2/m，路面不平顺情况的矢高α取为2 mm，ω =2πυ/L，L为车辆长度[14]，参照《公路工程技术标准》[15](JTG B01－2003)本文取为6 m。经简化，得:

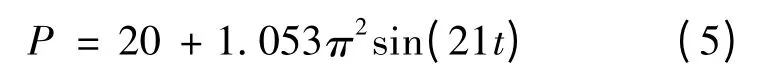
2.3 轮载接触面积的确定

在进行模拟前，轮胎的接地面积必须先予以确定，并做为文章后续分析的基础单位面积。在路面力学的分析和设计中，一般是假定轴载在接触面积上均匀分布，接触面积的大小，则取决于接触压力。一般来说，低压轮胎的接触压力要高于胎压，而高压轮胎的接触压力则小于胎压。由于重型轴载一般都采用高压轮胎，因此，现行的模拟中一般都是以胎压作为接触压力，这种假定方式是偏安全的，本文采用的亦是这个假定来确定车辆静载。

另一方面，轮胎和路面的接触面形状大致为椭圆形，但由于椭圆形荷载的计算较复杂，且模拟的时候较困难，因此一般将其简化为矩形，单轮作用时，实际情况大致如图2所示，为了便于计算，再将其简化为一个矩形当量面积，长为0.8721 L，宽为0.6 L，如图3所示。假设接触面积为A，则:

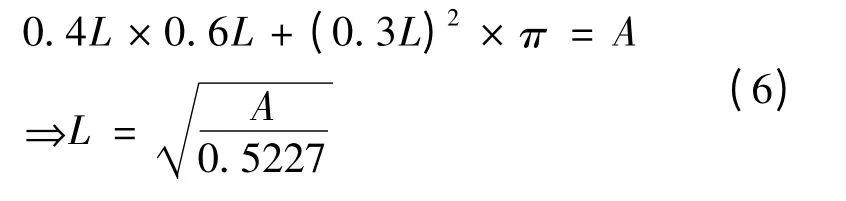
在经过以上分析后，本文取车轮与地面接触面积为0.3 m×0.2 m，在进行二维模拟的时候，取车胎宽度为0.2 m×2，两轮间距取为小轿车两轮距离1.8 m。

图2 轮胎和路面的接触面实际图

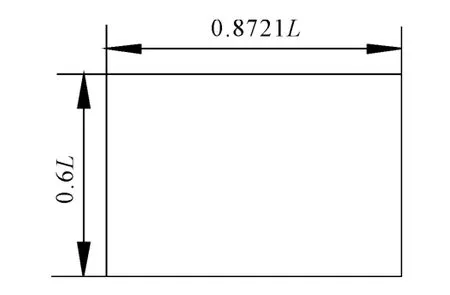
图3 轮胎和路面的接触面简化图

2.4 二维工况的模拟

2.4.1 模型的建立

本文选用有限元模拟软件Abaqus进行模拟，面层和基层均采用弹性模型，地基采用摩尔库伦模型，并参照扬州地区典型土体参数，取摩擦角和粘聚力分别为10°和35 kPa。其他各层次的参数如表1所示。其中面层选用沥青混凝土，基层为水泥碎石，底基层为石灰土，而基层采用软土地基，在具体分析中，各层次的叠加采用Abaqus中的生死单元功能，在将基层与面层的重力依次加载后，再进行交通荷载作用的模拟。各项参数取值如表1所示。

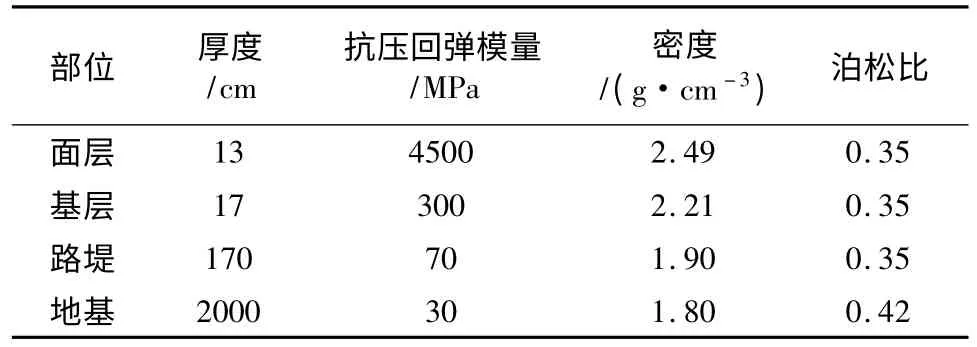
表1 道路结构各层材料参数

2.4.2 荷载大小的确定与施加的方式

交通荷载的加载分为静载(P0)的加载和动载(Pd)的加载两步进行。由于二维模型中假设路面的长度为1 m，车辆荷载的宽度为0.2 m，因此，二维情况下，作用的荷载为:

由于需要对土体中的应力及应变情况进行分析，本文模型尺寸采用的是一般二级道路尺寸，交通荷载的施加则参照了《公路工程技术标准》[15](JTG B01－2003)进行布置，在第一和第二分析步中施加各个道路层次重力，在第三步和第四步中施加交通荷载，这是为了防止由于荷载一次性施加可能对各个层次产生冲击作用。对于交通荷载的施加，本文采用静力荷载的方式施加交通荷载不变部分，而采用amplitude模块施加动荷载的可变部分。用于模拟的模型示意图如图4所示。

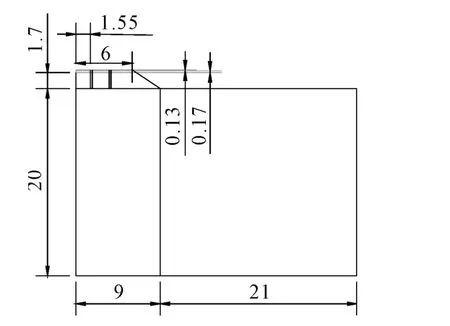
图4 二维模型尺寸示意图(单位:m)

2.4.3 模拟结果及分析

加载完毕后，针对加载的动载分析步结果进行分析，首先确定荷载影响深度。考虑最不利情况，即地基沉降最大的情况下，按竖向附加应力为自重应力的0.1倍土体自重应力的深度作为附加应力影响深度。取如图4所示单元进行影响深度的研究。通过图5所示的结果可以看到，由交通荷载产生的压力与0.1倍自重应力的交点大概在5 m深度处，准确数据为5.34 m处。这意味着模拟的交通荷载影响深度约为 5.34 m。黎冰等学者[16]的研究表明，交通荷载的影响深度为6 m～8 m之间，而本文所得结果为5.34 m，笔者认为这主要是由于上部荷载的模型使用了弹性材料模型，而未考虑沥青的其他性质所导致的。

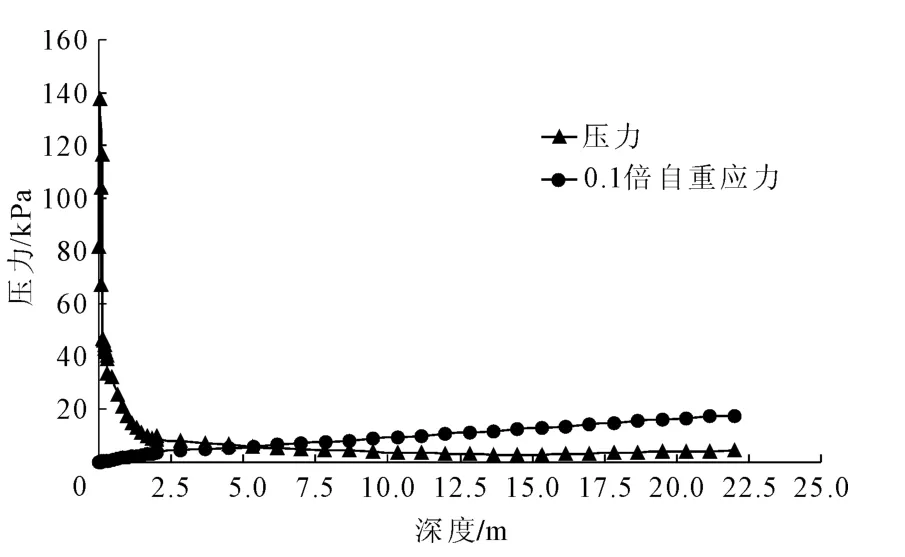
图5 荷载影响深度计算(二维)

取车轮荷载正下方道路层次不同深度的三个点(点1位于路面上，点2、点3位置为从路面向下依次递增0.1 m)进行竖直方向压力分析，结果如图6所示。由图6可以看到，荷载作用前期，波动较大，这是因为交通荷载首次施加后，弹性模型产生的微小震荡所导致的，而在作用后期荷载则平稳的按正弦曲线趋势发展。压力在竖向传递的过程中不断减少，在到达软土地基内部点3处时，其值已经很小，这表明模拟的交通荷载进行了有效的传递，且随着路面深度的增加而逐渐衰减。

为了进一步对不同深度的材料沉降进行研究，本文在车轮轨迹下沿着深度方向建立一条分析路径(path)，并利用加权平均值算法，得出了图7所示的位移随着深度变化的曲线，从图7可以看到位移随着深度的变化逐渐减小，并且出现了两个明显的拐点，都是在各层次分层处，这是由于两个层次弹性模量和密度都有很大的差别，从而产生了数据点的跳跃。从此处推测，面层和基层的分层处也应该有个数据跳跃点，经过放大处理后，的确存在相应的点。此外，在路堤层次(即第三个道路层次)的变形相对较大，这主要是因为文中将路堤层作完全弹性材料看待，且其弹性模量相对于路基路面层次较小的原因。同时可以看到，土体层次的位移随着深度的变化呈现了很好的规律性，这与应力扩散理论和土体的性质都是相符的。

图6 不同深度三个点竖向压力值(二维)

图7 深度－位移曲线(二维)

综合二维工况中上述两个曲线图，都符合相应材料的变形规律，且与实际道路中的受力情况基本类似，这说明，通过正弦荷载的方式对交通荷载进行模拟，在二维工况中是可行的。

2.5 三维工况的模拟

2.5.1 模型的建立

由于二维工况无法分析在道路纵向上车辆移动对道路整体产生的影响，故建立了三维模型。并主要在空间上分析交通荷载模拟方式的合理性。模型的断面尺寸以及所采用的模型材料参数和二维工况相同，而路面纵向长度定为50 m。对道路的加载采用移动荷载，由上文对华扬西路的调查中得出，模拟采用的车辆运行平均速度为72 km/h，即每辆车在设计长度方向上行进时间为2.5 s，以此来模拟车辆在路上移动的情况。模型中交通荷载的轨迹上每个单元的大小取为车轮荷载的面积，即0.3 m×0.2 m，如图8所示。为了减小计算量，本文仅模拟一辆车单次行驶通过道路时，对道路产生的各项影响。

2.5.2 荷载大小的确定与施加的方式

对于三维荷载中的移动荷载，其大小为:

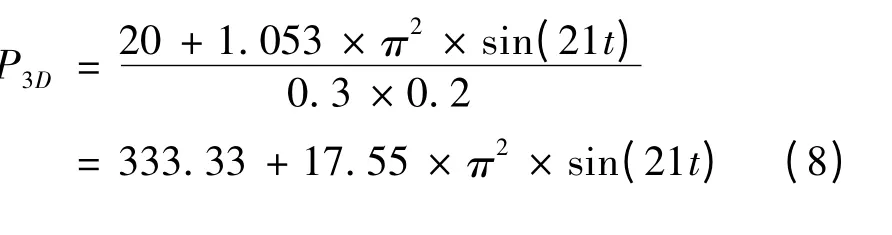
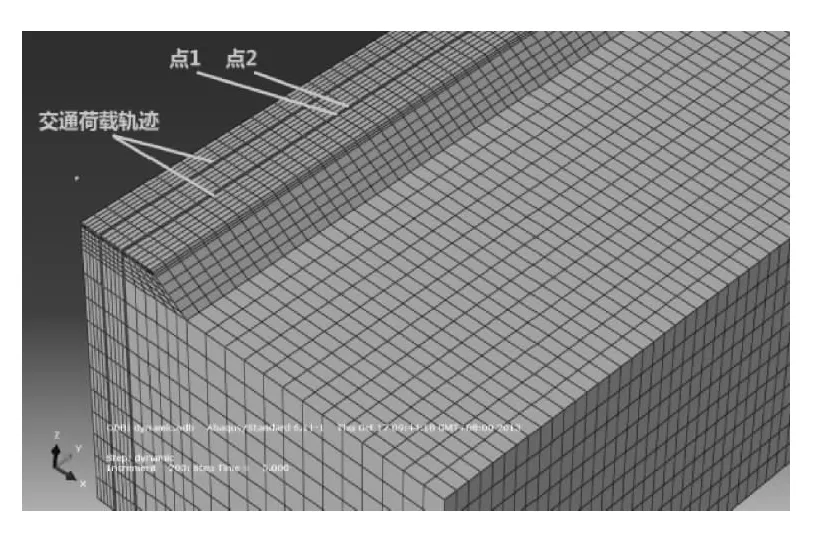
图8 三维模型图

为了实现荷载在车辆轨迹上的移动，本文使用了Abaqus中的用户子程序Dload来实现。在Dload子程序中，首先根据车辆行驶的时间，按照车辆行驶的速度，来判断车辆荷载作用的坐标;进而利用判断语句，根据交通荷载作用的面积在相应的面积范围内施加交通荷载，并利用车辆的速度来控制荷载的移动，从而达到了模拟交通荷载的目的。荷载大小如上文所述，随着时间不断变化的。三维工况建立的模型如图8所示，其中车辆轨道区进行了另外的划分，以便于分析以及 Dload定位荷载区域。

2.5.3 模拟结果及分析

同样的，取正弦荷载作用下的荷载作影响深度分析，如图9。从图9中数据可以看到，相对于二维工况，三维工况情况下，影响深度有所减少，仅在接近5 m处已经达到，准确数值为4.96 m。这主要是由于二维工况下是平面荷载，即纵向上荷载是不间断，连续分布的，而在三维荷载作用下，仅单辆车通过，即默认车辆荷载的作用时间不是持续不断的，车辆分布密度小于二维工况。从上述模拟结果看来，三维影响深度和二维工况的研究结果基本是一致的。

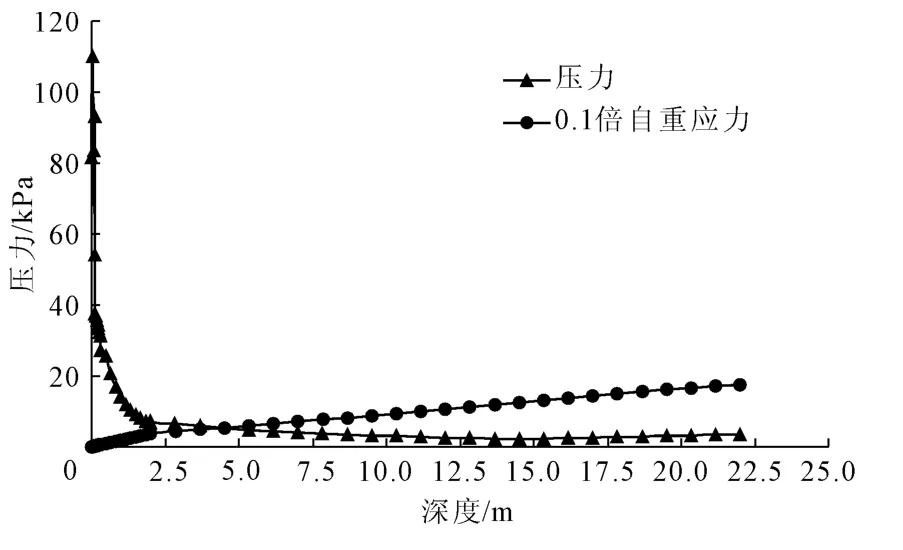
图9 交通荷载影响深度图(三维)

取图8所示的行车方向上车轮轨迹下相邻的2个点，用恒定荷载和正弦荷载分别进行加载，结果如图10、图11所示。从图10可以看出，恒定荷载作用的条件下，当荷载未移动到测点时，测点的压力也不为零，而是随着荷载的接近，呈上升趋势，当荷载到达测点上方时，达到峰值。并且可以看到，两点的峰值是一致的，在荷载逐渐远离测点时，两点所受到的压力也不为零，而是慢慢的减小。同时可以看到，荷载的值小于实际荷载公式的值，这主要是由道路层次对压力的分散作用所导致。

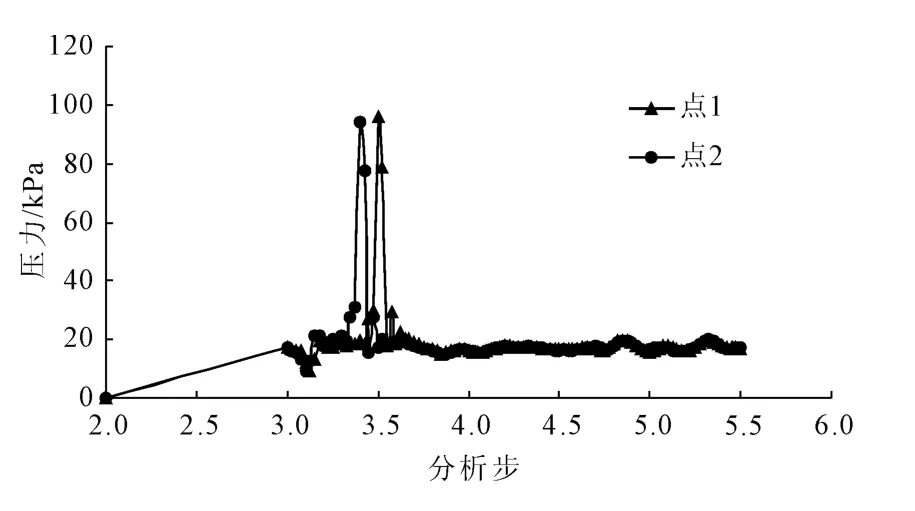
图10 相邻两点的压力－时间变化图(不变荷载)

图11 相邻两点的压力－时间变化图(正弦荷载)

与图10相比，图11中压力明显呈规律性变化;并且在两个测点的峰值也不同，与图10对比，这可以反映出荷载在移动中也在不断变化，符合正弦荷载随时间变化的特性，也符合道路所选用弹性材料的特性。

此外，本文的三维工况处理中，也是在道路上的车轮轨迹下沿着深度方向建立一条分析路径(path)，后处理得出了如图12所示的位移随着深度变化曲线。与二维工况作相比，两条曲线的趋势大致相同，数值也接近，并再次表明了交通荷载有效的传递。

图12 深度－位移曲线(三维)

综合上述影响深度曲线、压力变化曲线以及位移变化曲线的结果可知，用正弦曲线模拟荷载的方式在三维工况上可以很好的反映荷载在时间上以及空间上的变化。

3 结论

本文首先小结了交通荷载的特性，然后分别从二维和三维的角度对交通荷载进行了模拟，得出了以下结论:

(1)交通荷载是一种变化较复杂的动态荷载，并具有很大的重复性，采用具有可调参数的正弦荷载对其进行模拟，是一种比较合理的模拟方式;

(2)在影响深度以及压力传递的计算上，二维正弦荷载和三维静载都偏保守，只有三维正弦荷载更能反映实际情况;

(3)三维移动正弦荷载，优异于二维正弦荷载和三维移动恒载，是模拟交通荷载较为合理的一种方式。

[1]朱照宏，王秉纲，郭大智.路面力学计算[M].北京:人民交通出版社，1985.

[2]Walter R B.Nonliner finite element analysis of heavy loaded airfield pavement systems[C]//Applications of the Element Method in Geotechnical Engineering.New York:Elsevier，1972:657-693.

[3]Addis R R，Miht B.Vehicle wheel loads and road Pavement wear.In Heavy vehicle Road[C]//Technology，Safety and Policy.London:Thomas Telford， 1992:233-241.

[4]张春笋，吴进良，李晓军，等.边坡荷载作用下的边坡稳定性[J].重庆交通大学学报:自然科学版，2009，28(3):569-571.

[5]任有锋.大型车辆荷载在公路挡土墙设计中的换算[J].西北水电，2010，(4):55-58.

[6]徐 毅.交通荷载对高速公路路基影响的试验研究[D].南京:河海大学，2006.

[7]Hyodo M，Yasuhara K.Analytical Procedure of evaluation pore-water pressure and deformation of saturated clay ground subjected to traffic loads[C]//Proc 6th int conf of Numerical Methods in Geo-mechanics.Rotterdam:Bkalema，1988:653-658.

[8]陈 勇.交通荷载对低路堤高速公路路基影响的数值模拟研究[D].南京:河海大学，2006.

[9]李 伟，梁 波，马学宁.车辆荷载作用下高速公路路基路面动力研究[J].山西建筑，2007，33(2):289-291.

[10]黄永强.高速公路路基沉降及路面动力特性研究[D].长沙:中南大学，2010.

[11]张艳美，梁 波.几何不平顺条件下高速公路路基的动态响应[J].兰州铁道学院学报，2001，20(4):66-69.

[12]许文锋.交通荷载作用下地下通道初期支护的动力响应分析[J].水利与建筑工程学报，2008，6(3):18-20.

[13]凌建明.多轮荷载作用下跑道加铺层的力学响应分析[J].中国民航大学学报，2011，29(1):17-21.

[14]王常晶，陈云敏.交通荷载引起的静偏应力对饱和软黏土不排水循环性状影响的试验研究[J].岩土工程学报，2007，29(11):1742-1747.

[15]中华人民共和国交通部.JTG B01－2003.公路工程技术标准[S].北京:人民交通出版社，2003.

[16]黎 冰，高玉峰，魏代现，等.车辆荷载的影响深度及其影响因素的研究[J].岩土力学，2005，26(增刊):310-313.