风电-抽水蓄能联合系统的优化运行研究
2014-12-20王乐周章尉志勇宋洁刘海军
王乐,周章,尉志勇,宋洁,刘海军
(1. 智能电网研究院 中电普瑞科技有限公司,北京 102200;2. 北京市电力公司,北京 100062)
风电以其施工周期短、维护费用低、清洁无污染和不消耗任何燃料的优点取得了飞速发展。但是风电的间歇性、随机性、可调度性低的特点,可能影响电网的电能质量,如电压波动和闪变、谐波以及电网频率波动等[1-2]。公共连接点电压出现跌落时,风电机组会产生一系列过电压、过电流问题,大规模风电机组同时从系统解裂,可能导致连锁反应,严重影响电网的安全运行[3-4]。
将储能技术应用到风力发电系统可以有效抑制风电功率波动,提高风电的可控性,为电网提供优质电能[5-7]。超导储能、飞轮储能和电池储能容量比较小,因此它们不适合用作大规模风电的储能装置。压缩空气储能需要深挖地下空洞,投资比较大,并且造成环境污染,因此也不适合做大规模风电的储能装置[8-9]。抽水蓄能电站是目前最成熟的技术,容量不受技术限制,在有条件的风电场附近建立抽水蓄能电站,可以对风电调峰填谷、调频调相,还可以作系统备用容量[10-11],并且抽水蓄能电站具有独特的黑启动功能,在有条件的地区建立风电-抽水蓄能互补运行系统是解决风电发展的最优途径。日前,西班牙为了开发利用Hierro岛、Canary岛的风能资源,建设了相应的抽水蓄能电站与之联合运行,在德国、丹麦、美国等风能利用发达国家都不乏这样的工程实例[12]。
抽水蓄能电站抽水所需电能全部由风电场获得,当风电场有富余电能或电能不足时,控制系统根据现场实际情况对风电场和抽水蓄能电站进行相应控制,使得风力发电-抽水蓄能互补运行系统向电网输送功率在保证电能质量的前提下提高了经济效益。从电能质量考虑,使风电和抽水蓄能互补系统输出功率波动越小越好,但是过大的抽水蓄能容量会使投资和运行维护费用过高,对于储能容量的选取就变得非常重要[13-14]。本文研究的内容是如何在满足电能质量要求下,实现经济效益的最大化,并对抽水蓄能电站容量的选取提供一种可行的方法。
1 综合效益模型
1.1 经济效益模型
为了实现最大经济效益运行,需要确定各时段的风力发电机和抽水蓄能电站的工作状态。本部分模型建立是以经济效益最大化为基础的,在满足约束条件下,计算n时段各风电场中风力发电机组、抽水蓄能机组的出力值,从而得到风电—抽水蓄能互补系统的经济效益。模型中暂不考虑建立互补运行系统的投资成本和运行成本,则任意时刻的经济效益为风电场和抽水蓄能电站向电网输送的电能与抽水蓄能电站抽水所使用电能之差带来的经济效益。根据不同时刻风电场输送到电网的功率、抽水蓄能机组功率以及各时刻上网电价建立风电-抽水蓄能互补系统经济效益模型如下:
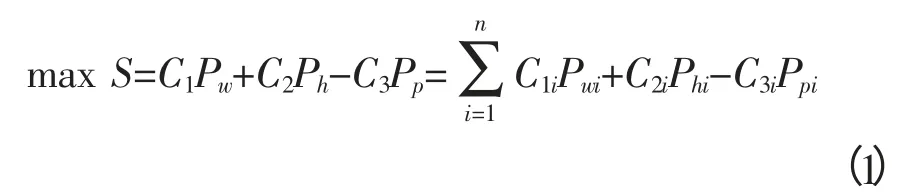
式中,max S为最大经济效益值;C1i为i时段风力发电上网电价;C2i为i时段抽水蓄能电站上网电价;C3i为i时段抽水蓄能系统抽水电价;Pwi为i时段风力发电机组出力;Phi为i时段水轮发电机出力;Ppi为i时段所有水泵抽水功率之和;n为时段总数。
约束条件如下:
1)考虑电网对风电的限制要求,预先设置风电场输送到电网的功率限制。因此风电-抽水蓄能互补系统对应时刻的风力发电机组系统输送到电网的功率和抽水蓄能发电系统输送到电网的功率之和满足电网限制,即:

式中,Pmin为电网限制下限;Pmax为电网限制上限;Pi为风电-抽水蓄能互补系统各时刻输送到电网的值。
2)风电场输出功率约束。风电场总装机容量上下限和风电机组效率决定了风电场的输出功率约束,即任意时刻风电场输出的功率都在风电场可输出功率上下限范围内:
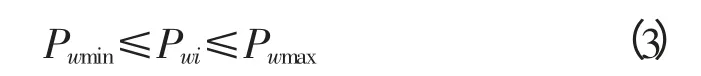
式中,Pwmin为风电场输送到电网功率下限;Pwmax为风电场输出到电网功率上限;Pwi为i时段风电场输出功率。
3)抽水蓄能电站的抽水功率约束。抽水功率约束根据抽水装机容量和抽水效率得到,即:

式中,Ppmin为抽水蓄能电站最小抽水功率;Ppmax为抽水蓄能电站最大抽水功率;Ppi为i时段抽水蓄能电站的抽水功率。
4)抽水蓄能机组的发电功率约束。发电功率约束由发电装机容量、发电效率和水库储能多少决定,即任意时刻抽水蓄能机组发电功率满足抽水蓄能发电装机约束和水库约束,即:

式中,Phmin为抽水蓄能机组最小发电功率;Phmax为抽水蓄能机组最大发电功率;Ei为各时刻水库储能值;t为每个时间段长。
5)抽水蓄能电站抽水与发电约束。抽水蓄能电站同时抽水发电理论上是可行的,但在实际情况中是不可取的,最主要原因是耗能,风电多余能量给抽水蓄能电站,此时转化效率最多为80%,那么风能就浪费了20%,并且还涉及维护等费用,如果同时抽水发电,则不如直接风电场发电,故抽水蓄能发电机组同时进行抽水发电没有意义。因此,在进行优化计算时,抽水工况与发电工况不同时进行。即:

6)风电场可利用风电功率约束。风电场可利用风电功率约束即任意时刻抽水功率和风电场输送到电网的功率都要小于对应的风电场可利用风电功率,即:

式中,Pvi为各时刻风电场可利用风能,即风电场未配置水力储能系统时可以直接转化为风电输出的功率。
7)水库储能约束。假定抽水蓄能电站上、下水库的蓄能库容不受限制,即抽水总量不受水库库容影响。水库i+1时刻储能值应该为第i时刻水库储能加上第i时刻的抽水总量并减去抽水蓄能机组第i时刻发电所需的水量。将水量约束转化为电量约束,即:

式中,ηp为抽水效率了;ηh为抽水蓄能机组发电效率。
1.2 电能质量模型
为了抑制风电输出功率的波动性和间歇性,减小风电场输出功率的波动性,以风力发电-抽水蓄能互补运行系统n时段输出功率波动最小为目标函数,建立了电能质量模型。目标函数如下:

式中,σmin为互补运行系统电能质量模型目标函数;Pwi为i时段风力发电机组出力;Phi为i时段抽水蓄能发电机组出力;Pavg为风电场n时段平均输送到电网的功率预测值;n为时段总数。
约束条件与1.1节经济效益模型中的约束条件相同,涉及风力发电功率、抽水蓄能功率和水库储能容量等方面。
1.3 综合效益模型
从经济效益方面考虑,控制目标是实现经济效益最大化。从电能质量方面考虑,控制目标是互补系统向电网输送功率波动最小。因为最大经济效益和最小输出功率波动的目标函数不同,得出的控制变量的值也是不同的,即风力发电机和抽水蓄能的工况不同。因此,在实际运行中应该综合考虑经济效益和电能质量。
本文建立的综合效益模型是在满足一定电能质量的前提下,实现经济效益最大化。具体实现是将电能质量约束加入到经济效益最优化模型的约束条件中。其中综合效益模型目标函数如下:

约束条件:

式中,σs为各个时段功率波动方均根的最大限值。
综上所述,以功率波动为约束条件,以最大经济效益为目标函数,对综合效益模型进行求解,即可得到综合效益模型下的最优调度方案。
2 计算流程
采用文中提到的经济效益、电能质量以及综合效益模型进行求解分析可以归结为一定约束条件下的最优化问题,而遗传算法作为一种全局优化概率算法,在最优化求解中有经典应用。遗传算法是一种借鉴生物界自然遗传机制的高度并行、随机、自适应的全局优化概率搜索算法。遗传算法是从群体出发开始的并行操作,而不是从一个点开始,因而可以有效地防止搜索过程收敛于局部最优解,有较大可能求得全局最优解。由于遗传算法的操作均使用随机概率的方式,而不是确定性的规则,随机选取数据的概率计算更具说服性。
本文选择遗传算法进行仿真计算,计算流程如图1所示,计算步骤为:
1)输入基本数据。如风电场预测最大输出功率曲线,电网调度要求、峰谷电价时刻、约束条件、迭代步数等。
2)选择需要优化的模型,确定目标函数。
3)对抽水蓄能机组各时刻抽水功率赋予初值。
4)根据各时刻确定的抽水功率,约束条件得到风电场各时刻输出功率和抽水蓄能机组发电功率。
5)根据各时刻风电机组输出功率、抽水蓄能机组抽水功率、抽水蓄能机组发电功率以及峰谷电价计算目标函数值,并记录目标函数最大值。
6)根据迭代步数,判断迭代过程是否结束。如果迭代过程没有结束,则通过遗传算法进行选择、交叉、变异操作,对抽水蓄能机组各时刻抽水功率进行修正,转到步骤(4)、(5)继续运算。

图1 风电-抽水蓄能互补运行系统计算流程图Fig. 1 Calculation flowchart of hybrid wind power and pumped hydro storage system
7)计算结束,输出最优化结果。
3 仿真分析实例
以黑龙江地区一座装机容量为50 MW风电场为背景进行实例分析。表1列出了该风电场2008年1月3日预测的风电场输出功率各时刻值。 假设为风电场配置的抽水蓄能电站为30 MW。该互补系统分析的各主要基本参数见表2。
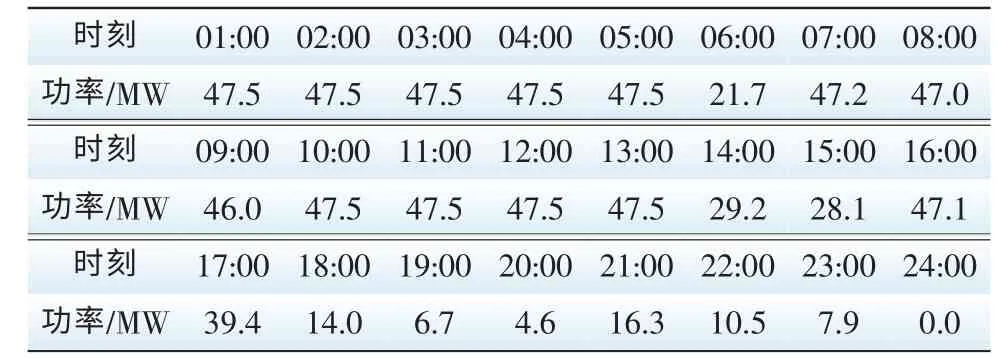
表1 风电场2008年1月3日预测的风电场输出功率各时刻值Tab. 1 Predicted power output of the wind farm on March 1,2008
利用遗传算法,对经济效益模型进行仿真计算,风力发电-抽水蓄能互补运行系统各时刻输出功率如图3所示,各时刻输出均满足电网上下限约束,在电价高峰时段输出以最大功率输出,而在谷价和平价时段输出明显降低。互补运行一天所得最大经济效益为0.488 44×106元。而风电场没有配备抽水蓄能电站一天所得经济效益为0.395 88×106元。由图2和图3对比可知,该曲线输出与仅有风电场相比输出平滑了许多。

表2 互补系统分析的各主要基本参数Tab. 2 Main parameters of the hybrid system
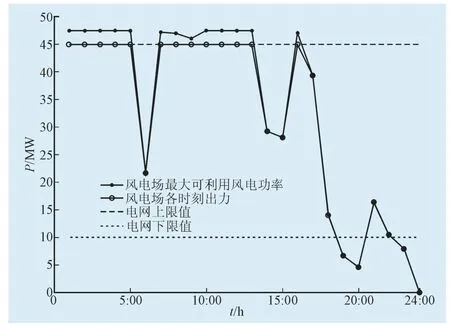
图2 仅有风电场时向电网输送的功率曲线Fig. 2 Power curve when only wind farms send power to the power grid
利用遗传算法,对电能质量模型进行仿真,以输出功率波动最小为目标函数,到互补系统经济效益为0.354 40×106元,一天输送到电网的功率输出标准差为3.150 7 MW,与仅有风电场时的功率输出标准差为80.295 0 MW相比小了很多,各时刻输出波动很小,且各时刻输出均围绕预测日平均值33.04 MW输出,即抽水蓄能电站的配置减小了输出功率的波动,提高了电能的质量。
对综合效益模型进行仿真,得到互补运行系统经济效益为0.488 2×106元,图4为互补运行系统输出功率曲线,与经济效益模型中互补运行系统经济效益0.488 44×106相比效益稍有降低,图4与图2相比输出功率整体波动变小,提高了电能质量。而图4与前面以电能质量为目标函数仿真得到的图3进行比较发现,电价高时刻有功功率输出明显提高。且互补系统以图4输出所得经济效益0.488 2×106元与以图2输出所得经济效益0.354 40×106元相比明显增大。因此,综合效益模型可以在满足电能质量要求的前提下,使经济效益最大化。

图3 风力发电-抽水蓄能互补运行系统各时刻输出功率曲线(最大经济效益)Fig. 3 Output power curve of the hybrid wind power and pumped hydro storage system(with maximum economic benefits)

图4 风力发电-抽水蓄能互补运行系统各时刻输出功率曲线(最优电能质量)Fig. 4 Output power curve of the hybrid wind power and pumped hydro storage system(with the best power quality)
4 结论
本文对风电抽水蓄能互补系统的优化运行进行了研究,建立了经济效益模型、电能质量模型和综合效益模型,将3个模型归结为一定约束条件下的最优化问题。利用遗传算法对模型进行了仿真计算,仿真结果表明:综合效益模型是在满足电能质量要求的约束条件下,实现经济效益最大化,兼顾了电能质量模型的平抑风电功率功能和经济效益模型的经济性。

图5 风力发电-抽水蓄能互补运行系统各时刻输出功率曲线(综合效益模型)Fig. 5 Output power curve of the hybrid wind power and pumped hydro storage system(with comprehensive benefits model)
由于抽水蓄能电站的投资和运行费用作为固定费用,不会对优化运行的控制策略产生影响,所以制定优化运行策略时没有进行考虑这部分固定费用。但是抽水蓄能电站的容量会对经济效益的大小产生影响,所以抽水蓄能电站容量的选取是研究风电抽水蓄能互补运行的一个研究重点。
[1] 张步涵,曾杰,毛承雄,等. 电池储能系统在改善并网风电场电能质量和稳定性中的应用[J]. 电网技术,2006,15: 54-58.ZHANG Buhan,ZENG Jie,MAO Chenxiong,et al.Improvement of power quality and stability of wind farms connected to power grid by battery energy storage system[J].Power System Technology,2006,15: 54-58(in Chinese).
[2] 于芃,周玮,孙辉,等. 用于风电功率平抑的混合储能系统及其控制系统设计[J]. 中国电机工程学报,2011,31(17): 127-133.YU Peng,ZHOU Wei,SUN Hui,et al. Hybrid energy storage system and control system design for wind power balancing[J]. Processing of the CSEE,2011,31(17): 127-133(in Chinese).
[3] 陈虎,孟克其劳,马建光. 基于MATLAB的风力发电机组建模和仿真研究[J]. 节能技术,2012,30(1):24-28.CHEN Hu,MENG Keqilao,MA Jianguang. The modeling and simulation study of wind turbine based on MATLAB[J].Energy Conservation Technology,2012,30(1):24-28(in Chinese).
[4] 赵吴鹏,王彪. 传动链模型对风机低电压穿越能力的影响[J]. 节能技术,2012,30(4):335-352.ZHAO Wupeng,WANG Biao. Drive-train model for wind turbine LVRT capability influence[J]. Energy Conservation Technology,2012,30(2): 335-352(in Chinese).
[5] 贾宏新,张宇,王育飞,等. 储能技术在风力发电系统中的应用[J]. 可再生能源,2009(6):10-15.JIA Hongxin,ZHANG Yu,WANG Yufei. et al. Energy storage for wind energy applications[J]. Renewable Energy,2009(6):10-15(in Chinese).
[6] 李蓓,郭剑波. 平抑风电功率的电池储能系统控制策略[J]. 电网技术,2012(8): 38-43.LI Pei,GUO Jianbo. A control strategy for battery energy storage system to level wind power output[J]. Power System Technology,2012(8): 38-43(in Chinese).
[7] 陈满,陆志刚,刘怡,等. 电池储能系统恒功率削峰填谷优化策略研究[J]. 电网技术,2012(9): 232-237.CHEN Man,LU Zhigang,LIU Yi,et al. Research on optimal peak load shifting strategy of battery energy storage system operated in constant power mode[J]. Power System Technology,2012(9): 232-237(in Chinese).
[8] HADJIPASCHALIS I,POULLIKKAS A,EFTHIMIOU V.Overview of current and future energy storage technologies for electric power applications[J]. Renewable and Sustainable Energy Reviews,2009(7):36-39.
[9] IBRAHIM H,ILINCA A,PERRON J. Energy storage systems:characteristics and comparisons[J]. Renewable and Sustainable Energy Reviews,2008(9):23-26.
[10] PE X,REZ-DI X,AZ J I,et al. Optimal short-term operation and sizing of pumped-storage power plants in systems with high penetration of wind energy[C]// Proceedings of the 7th International Conference on the European Energy Market(EEM),2010.
[11] FENG G,HALLAM A,CHIEN-NING Y. Wind generation scheduling with pump storage unit by collocation method[C]//Proceedings of the IEEE Power & Energy Society General Meeting,2009.
[12] DELIMUSTAFIC D,ISLAMBEGOVIC J,AKSAMOVIC A,et al. Model of a hybrid renewable energy system: control,supervision and energy distribution[C]. 2011 IEEE International Symposium on,Industrial Electronics,2011: 1081-1086.
[13] 李碧辉,申洪,汤涌,等.风光储联合发电系统储能容量对有功功率的影响及评价指标[J]. 电网技术,2011(4):123-128.LI Bihui,SHEN Hong,TANG Yong,et al. Impacts of energy storage capacity of configuration of HPWS to active power characteristics and its relevant indices[J]. Power System Technology,2011(4): 123-128(in Chinese).
[14] 韩涛,卢继平,乔梁,等. 大型并网风电场储能容量优化方案[J]. 电网技术,2010(1): 169-173.HAN Tao,LU Jiping,QIAO Liang.et al.Optimized scheme of energy-storage capacity of grid-connected large-scale wind farm[J].Power System Technology,2010(1): 169-173(in Chinese).
