一个析取等值式及其相关逻辑问题的学术对话

马雷，张建军，翟玉章，杜国平

（1.东南大学 人文学院，江苏 南京 211189；2.南京大学 哲学系，江苏 南京 210093；3.中国社会科学院 逻辑研究所，北京 100732；4.南京师范大学 哲学系，江苏 南京 210046）

一、马雷与张建军的问答

马雷（以下简称“马”）：

我们能不能说“A∨B∨C 永真，当且仅当A∨B永真或者A∨C永真”？A、B、C代表单一命题和代表复合命题对于这个论断有区别吗？

张建军（以下简称“张”）：

不知这个问题是针对何具体问题提出的。

“A ∨B∨C 永真，当且仅当A ∨B 永真或者A ∨C 永真”，一般地说是不对的。如“p∨q∨非q”永真，但p∨q和p∨非q都不永真，只能得“（p∨q）∨（p∨非q）”这个析取式永真。这对单一命题和复合命题都是一样的②。

马：我们可以说“如果A∨B 永真或者A∨C 永真，那么A∨B∨C永真”，可以通过论证“A∨B永真或者A∨C永真”来论证“A∨B∨C永真”，是吧？但是，不能倒过来论证，因为两者没有等值关系。就是说，克劳斯著《形式逻辑导论》③272页中这样的论证思路还是对的。为了论证

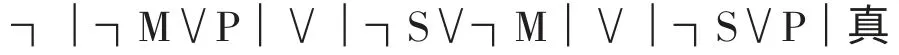
可以论证或者

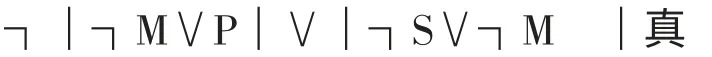
或者

他还是错在随便脱去竖号。奇怪的是，在这个例子中，他不同意原式三大项同时脱去竖号，再运算，而是主张分解开来再脱去竖号运算。张老师举的这个例子特别简洁明白，能说明问题。但是，如果做个限定，A∨B∨C 里面排除出现q∨非q 的情况，那么原等值式是否就对？

张：我手头没有克劳斯的书。这里可能要区分真和永真。A∨B∨C与（A∨B）∨（A∨C）是等价的，一个真另一个必真，一个永真另一个必永真。从（A∨B）∨（A∨C）为真可得其析取支至少一真，但从（A ∨B）∨（A ∨C）永真得不出其析取支至少一个永真④。

当然你说的倒过来的论证是对的。

马：问题还没搞明白，请看：

对于任何动物而言，它头上的毛一定有一个是动物的

马是动物

所以，对于任何马而言，它的头上的毛一定有一个是马的

对于任何真的析取式而言，它的析取支一定有一个是真的

永真是一种真

所以，对于任何永真的析取式而言，它的析取支一定有一个是永真的

如果前面一个推理正确，那后一个也正确。为什么后一个真前提却推出错的结论？除非您认为前一个推理不对。

张：前一个推理是有效的，但后一个推理与之不同。永真并不是一个真值，只能说永真语句在任何可能世界中都取“真”值。（故不能说永真是一种真，而只能说永真语句是一种真语句）⑤

永真析取式是说它的析取支无论在任何情形（任何可能世界）都至少一真，但不是至少一“永真”。请考虑：

A∨非A 肯定永真，只能得出析取支必至少一“真”，而得不出至少一“永真”。

马：我也怀疑“永真是一种真”有问题，但不知在什么地方出了问题，您这样说，我就清楚了。你说“永真语句是一种真语句”，那么下面的推理对吗？

对于任何析取式而言，如果它是真语句，则它的析取支一定有一个是真语句

永真语句是一种真语句

所以，对于任何析取式而言，如果它是永真语句，则它的析取支一定有一个是永真语句

该推理与下面您认为正确的推理有什么不同吗？

对于任何动物而言，它头上的毛一定有一个是动物的

马是动物

所以，对于任何马而言，它的头上的毛一定有一个是马的。

张：马和动物这个推理有效，是因结论本身就是逻辑真理（马的头上的毛是马的毛），与马和动物的种属关系无关。

从种属关系立论，从任一永真析取句都是真析取句、任一真析取句的析取支至少一真，只能得一永真析取句的析取支至少一真（不能得永真）。

王路以前主张把truth译为真而不译为真理，我一直反对。因为“真”是一个真值，truth（真理）是真命题或真语句，二者不可混为一谈。你的讨论为此提供了新的佐证⑥。

马：很赞同您关于真值和真理的区分。又有一个问题，是不是我以前没有注意到？

对于任何动物而言，它头上的毛一定有一个是动物的

马是动物

所以，对于任何马而言，它的头上的毛一定有一个是马的。

您是说这是一个有效推理（因为结论是逻辑真的），但结论不能从前提中推出来。就是说前提与结论没有必然联系，对吧？如果是这样，那对“有效推理”的定义是什么呢？凡结论为逻辑真的推理都是有效推理？就是说前提与结论（或者说前件与后件）之间构成了一个真的逻辑关系，但前提不一定能必然推出结论？就是说不符合推理规则的推理也可能是有效推理？有效推理与正确推理应当区别开来吗？

张：从有效推理定义说，若前提矛盾或结论永真就可判定是有效推理，当然这种推理乃是“空虚”有效。经典逻辑的有效式可写成永真的实质蕴涵式⑦。前提矛盾或后件永真都是永真的实质蕴涵式。

正确推理看怎么定义，若我们要求前提一定真，则前提矛盾的必不正确，后一种要看具体情况。

马：谢谢您帮我澄清概念！我理解的正确推理就是符合推理规则的推理，这可能是一种传统逻辑观念，而不是现代逻辑观念。

刚刚发现，就推理规则而言，关于马和动物的推理，从前提确实推不出结论。

正确的推理：

动物的毛有一个是动物的

马是动物

所以，马的毛有一个是动物的

错误的推理：

马的毛有一个是动物的

马是动物

所以，马的毛有一个是马的

通过联锁三段论可以论证。

张：这很对，类似于从马是动物，可推出所有马的头都是动物的头。

二、马雷与翟玉章的问答

马：我们能不能说“A∨B∨C 永真，当且仅当A∨B 永真或者A∨C 永真”？A、B、C 代表单一命题和代表复合命题对于这个论断有区别吗？

翟玉章（以下简称“翟”）：

很好的问题。答案是肯定的。

这里的A、B、C 可以理解为语句模式，比如“p”,“p 或q”, “如果p,那么q”,“既非p,也非q”等（其中的“p”,“q”是所谓语句模式字母，意思是它们的位置可以为具体的语句所代替）。现在来表明你的结论。（1）如果【A或者B】是有效模式（又称永真式），那么对该模式中模式字母无论用什么语句来代替，所形成的语句都是真的。因此在任何解释下，不论C是否为真，【A或B或C】也是真的（因为【A或B或C】的真值在【A 或B】为真的情况下即为真），而这正是【A或B或C】为有效模式的含义。（2）同样可以说明：如果【A或C】是有效模式，那么，【A或B或C】也是有效模式。综合（1）和（2）可知，【A或B或C】为有效模式的充分条件是【A或B】或【A或C】是有效模式。

现在进一步说明这也是必要条件。如果【A或B或C】为有效模式，那么，在任何解释下，A,B,C 三者至少之一为真。（1）如果A为真，显然，【A或B】和【A或C】都为真，既然都为真，则至少之一为真可确保，即【A 或B】为真或【A 或C】为真。（2）如果B 为真，那么【A 或B】为真；既然【A 或B】为真，那么【A 或B】为真或【A 或C】为真。（3）如果C 为真，说明同（2）。综合（1）、（2）、（3），【A 或B 或C】为有效模式的必要条件是【A或B】或【A或C】是有效模式。

综合上面两段，可知结论成立：A∨B∨C 永真，当且仅当A∨B永真或者A∨C永真。

以上说明很直观。只运用了“或者”一词的含义：“p 或者q”为真当且仅当“p”为真或“q”为真，以及有效模式（永真式）的定义：一个模式是有效的，当且仅当无论对该模式中的字母作何解释，所得到的语句都是真的；比如模式“p或者非p”是一个有效模式，因为无论对“p”作何解释（无数种解释可以归结为两种，即用真语句代替“p”和用假语句代替“p”),得到的语句都是真的，而模式“p或者非q”不是有效模式，因为当我们分别用假语句（比如，“中国在美洲”）和真语句（比如，“加拿大在美洲”）来解释“p”和“q”时，得到的是一个复合的假语句（比如“中国在美洲或者加拿大不在美洲”）。

另外，再重申一下A,B,C 和“p”,“q”,“r”的区别。前者可以是复杂模式，而后者只是模式字母，是最简单的模式。为什么前者无引号，后者有引号？原因：A,B，C是名词，是模式的名称；而p,q,r则是语句模式（当然是最简单的模式），起着语句的作用，但代替这些小写字母的可以是复杂的语句。因此，严格说来“A或者B”是不合句法的，因为“或者”联结的是两个语句，而不是两个名字。你可能注意到，我使用了“【A或者B】”这样的表达式，意思是这个语句是由A和B所代表的语句所形成的复合句。“p或者q”是合格的表达式，因为这里的小写字母所起的就是语句的作用，而不像A，B 那样，只是起语句名称的作用。这里的区别实际上就是对象和对象的名称之间的区别，这在很多情况下是一目了然的，如“北京”和北京的区别，但在数学和逻辑里，这个区别有时会迷失，一流的逻辑学家如罗素者都曾经有过这样的混淆。

马：谢谢你的详细分析！我的问题有些歧义，现在改成“A∨B∨C永真，当且仅当A∨B和A∨C当中至少有一个是永真的”。如果这样表述的话，您还认为正确吗？

翟：仍然正确。

马：假定A=┐（┐M∨P）；B=┐S∨┐M；C=┐S∨P，则

A∨B=（┐M∧┐P）∨（┐S∨┐M）=（┐S∨M∨┐M）∧（┐S∨┐M∨┐P）。该式不是永真的。

A∨C=┐（┐M∨P)∨(┐S∨P)=（M∧┐P）∨（┐S∨P）=（┐S∨M∨P）∧（S∨P∨┐P）。该式也不是永真的。

A∨B∨C=┐（┐M∨P）∨（┐S∨┐M）∨（┐S∨P）=（M∧┐P）∨（┐S∨┐M）∨（┐S∨P）?=（┐S∨M∨┐M∨P）∧（┐S∨M∨P∨┐P）。该式是永真的。

就是说原等值式不正确。怎么解释？

翟：第一封回信中关于必要条件的证明是错误的。

现在进一步说明这也是必要条件。如果【A或B或C】为有效模式，那么，在任何解释下，A, B, C三者至少之一为真。（1）如果A 为真，显然，【A 或B】和【A 或C】都为真，既然都为真，则至少之一为真可确保，即【A 或B】为真或【A 或C】为真。（2）如果B 为真，那么【A或B】为真；既然【A或B】为真，那么【A或B】为真或【A 或C】为真。（3）如果C 为真，说明同（2）。综合（1）、（2）、（3），【A 或B 或C】为有效模式的必要条件是【A 或B】或【A 或C】是有效模式。

黑体字之前的论证都是正确的。但黑体字的结论是错的。我们只能说， 综合（1）、（2）、（3），如果【A 或B 或C】是有效模式，那么在任何解释下，【A或B】和【A 或C】中至少有一个是真的，而这其实只是说【（A或B）或（A或C）】是有效模式。而说【（A或B）或（A 或C）】是有效模式，并不等于说 【A 或B】或【A 或C】是有效模式。简单的反例是：虽然“p 或非p”是有效模式，但“p”和“非p”都不是有效模式。逻辑上的事情有时很微妙，稍有疏忽就会出错。我原是一步一步说明的，但最后出现了跳跃，错误正出现在此跳跃中。

非常感谢您通过一个反例（即证伪法）纠正我的这一错误。

马：你认为下面的推理对不对？

对于任何动物而言，它头上的毛一定有一个是动物的

马是动物

所以，对于任何马而言，它的头上的毛一定有一个是马的。

翟：有效推理。从直观上就很清楚。但我还是将它推导如下。

两个前提和结论的同步结构是：

前提一：（x)(Fx→(Ey)(Gyx(Ez)(FzGyz)))

前提二：（x)(Hx→Fx)

结论：（x)(Hx→(Ey)(Gyx(Ez)(HzGyz)))

Fx:x是动物，Gxy:x是y头上的毛，Hx:x是马。

为了表明这是一个有效的推理，只需表明肯定前提而否定结论会导致矛盾即可。

1.（x）(Fx→(Ey)(Gyx(Ez)(FzGyz)))...前提一

2.（x）(Hx→Fx)...前提二

3.-（x）(Hx→(Ey)(Gyx(Ez)(HzGyz)))...结论的否定

4.（Ex）-(Hx→(Ey)(Gyx(Ez)(HzGyz)))...3的前置式

5.-（Ha→(Ey)(Gya(Ez)(HzGyz)))...4，特称例化

6.Ha-(Ey)(Gya(Ez)(HzGyz))...5，真值函项变换

7.Ha...6，合取的性质：如果合取为真，那么任一合取肢也为真。

9.-(Ey)(Gya(Ez)(HzGyz))...6，合取的性质

10.(y)-(Gya(Ez)(HzGyz))...9的前置式

11.Ha→Fa...2,全称例化

12.Fa...7,11,肯定前件推理

13.Fa→(Ey)(Gya(Ez)(FzGyz))...1,全称例化

14.(Ey)(Gya(Ez)(FzGyz))...12、13，肯定前件推理

15.Gba(Ez)(FzGbz)...14,特称例化

16.Gba...15,合取的性质：如果合取为真，那么任一合取支为真。

17.-(Gba(Ez)(HzGbz))...10，全称例化

18.-Gba∨-(Ez)(HzGbz)...17,真值函项变换（德摩根定律）

19.-Gba∨(z)-(HzGbz))...18,移置律（将析取式后一个析取支实现量词前置）

20.(z)(-HzGbz∨-Gba)...19,移置律（将整个析取式实现量词的前置）

21.-HaGba∨-Gba...20，全称例化

22.-Gba...21,7，真值函项变换

23.Gba-Gba（矛盾）...22、16

马：你的有效推理的定义是不是这样：“从有效推理定义说，若前提矛盾或结论永真就可判定是有效推理，当然这种推理乃是‘空虚’有效。经典逻辑的有效式可写成永真的实质蕴涵式。前提矛盾或后件永真都是永真的实质蕴涵式。”（张建军语）

我理解的正确推理是符合推理规则的推理，就是如果前提真，并且符合推理规则，结论一定真；如果前提假，并且符合推理规则，则结论必然假⑧。

翟：你对我的理解是正确的。但你我之间其实并无分歧。照你的理解，一个推理是有效推理，当且仅当结论可以逻辑地从前提中推导出来，或只要前提真，那么结论就一定真。但我们如何判断能否逻辑地推导出来呢，或者如何判断在前提真的情况下结论一定真呢？其核心方法仍是判断由前提作前件而结论作后件的条件句是否为逻辑真。另外将条件句称为（实质）蕴涵句是不准确的。蕴涵句是元语言层面的东西，它谈的是两个语句之间的关系。而条件句一般并不是关于语句的。当然两者之间有联系，具体地说：任何一个条件句都对应一个实质蕴涵句。举例：“如果明天天不下雨，我就去爬山”这个条件句如果是真的，那么对应的蕴含句也是真的：语句“明天天不下雨”蕴含语句“我明天去爬山”。

马：我可以通过联锁三段论证明下面的推理无效，就是按照正确规则从前提推不出结论。

对于任何动物而言，它头上的毛一定有一个是动物的

马是动物

所以，对于任何马而言，它的头上的毛一定有一个是马的。

正确的推理：

动物的毛有一个是动物的

马是动物

所以，马的毛有一个是动物的

错误的推理：

马的毛有一个是动物的（把前面的结论作为大前提）

马是动物

所以，马的毛有一个是马的

翟：“动物的毛有一个是动物的”与你的原先的前提“对于任何动物而言，它头上的毛一定有一个是动物的”并不是一回事。前者说的是：存在着如此这般的对象，这个东西既是动物的毛，同时又是动物的毛，简化成：存在着动物的毛。但后者并不蕴含存在着动物的毛这一点，它只是说，任何对象如果是动物，那么将存在着既是它的毛又是动物的毛（这意味着可能是别的动物的毛），这里并没有说到是否存在着毛的问题，至多只是有条件地肯定存在着这样的东西。另外，这个推理严格说来并不是三段论推理，因为第一个前提实际上只有一个概念，即“动物的毛”，另外整个推理有四个概念：动物的毛、马、动物、马的毛。更重要的是，这并不是一个有效推理。如果你将“马是动物”替换成“永动机是动物”（这是真的），结论将是“永动机的毛有一个是动物的”，这说的是存在着既是永动机的毛又是动物的毛的东西，但这样的东西显然是不存在的。

马：“马是动物”是否等值于“马的毛是动物的毛”？或“马的头上的毛是动物头上的毛”？

翟：马是动物：(x)(如果x是马，那么x是动物）

马的毛是动物的毛：（x)(如果x是马的毛，那么x是动物的毛），进一步地：（x)(如果(Ey)(y 是马而且x是y的毛），那么 (Ey)(y是动物而且x是y的毛))

可以证明，这是一个有效推理。

具体地说，就是要证明体现：“(x)(Fx→Gx)”蕴含“(x)((Ey)(FyDyx→(Ey)(GyDyx))”

类似的推理，16 世纪的逻辑学家Joachim Jungius曾经考察过，不过他的例子是：

从“圆是图形”推导出“画圆的人是画图形的人”，这个推理涉及关系：x画y。

他还有另外一个例子：从“偶数的平方是偶数”和“6 是偶数”推导出“6 的平方是偶数”。这看上去极像一个三段论，但事实上并不是。要说明这一推理，要用到关系：x是y的平方。

同样，我们也可以从“马是动物”推出“马的头是动物的头”，再从后者推出“（马的头）的毛是（动物的头）的毛”。

马：一般人承认从“马是动物”推出“马的毛是动物的毛”，但没有说明从“马的毛是动物的毛”能否推出“马是动物”。

翟：确实，反过来的推理并不成立。举例：即使每一个美国人的财产都是中国人的财产，但美国人依然可以不是中国人。

马：“每一个美国人的财产都是中国人的财产”是什么意思？

“马的毛是动物的毛”这个意思比较含糊。准确理解应为“马身上长的毛是动物身上长的毛”，这与“马所拥有的东西是动物所拥有的东西”（比如“马的鞍子是动物的鞍子”）是不同的。如果这样理解，会怎么样？

翟：每一个美国人的财产是中国人的财产。

（x)(如果x 是美国人的财产，那么x 是中国人的财产）

（x)(如果(Ey)(y 是美国人而且x 是y 的财产），那么(Ey)(y是中国人而且x是y的财产))

你可以看到，这与“（x)(如果(Ey)(y是马而且x是y 的毛），那么(Ey)(y 是动物而且x 是y 的毛))”（即“马的毛是动物的毛”），在结构上是一样的。

你所说的区别，多数情况下只是一种修辞上的区别。你的两种说法，马的毛是动物的毛，马身上长的毛是动物身上长的毛，前者说：和马发生某种关系的事物同时也是和动物发生同样关系（x 是y 的毛）的事物，后者说的也是：和马发生关系的事物同时也是和动物发生同样关系的事物（x 长在y 上）。虽然“x是y的毛”和“x长在y上”的含义并不同，但它们将分别得到同样的处理。当然，如果这两种关系发生在同一个论说中，比如“这虽然是属于我的毛，但却不是我身上长着的毛”，将需要用不同的模式字母表示：Fxy而且-Gxy。

马：我是问“每一个美国人的财产是中国人的财产”的内涵是什么？好像美国人是强盗。你对此句的逻辑分析很细致，推理也对。我的疑惑是：你能举出反例说明从“X 身上长的Z 是Y 身上长的Z”推不出“X是Y”吗？

翟：我这个例子也是有感而发的。现在网上有一种议论，认为美国人在发动一种金融战争掠夺中国人的财富！

你让我举一个毛的例子，那也能做到的。设想，人身上并没有毛，但科学家经过研究认为，人身上要是有毛的话，可以防止某种疾病。于是人们纷纷以植入狗毛为荣。于是我们有下面的真前提：人身上长的毛都是狗身上长的毛⑨。但即使如此，人仍然不是狗。

马：你这个例子好像有些诡辩。你增加了前提。你的推理前提是：

1.人身上植入了狗的毛

2.人身上长的毛都是狗身上长的毛

“人不是狗”的结论是从两个前提合推出来的。

翟：我所说的是，从逻辑的角度看，单单从“人身上长的毛是狗身上的毛”是推不出“人是狗”的，就像单单从“美国人的财富是中国人的财富”推不出“美国人是中国人”一样。结合到你的例子，你也不能从“马身上长的毛是动物身上长的毛”推出“马是动物”一样，尽管反过来的推理是成立的。

我的意思并不是说从“人身上长的毛是狗身上长的毛”再加上“人身上植入了狗的毛”可以推出“人不是狗”。事实上，这两个前提并不能推出这一结论。显然，第一个前提和第二个前提在逻辑上并无相关性。“植入”对第一个前提来说完全是一个陌生的词项。

马：可能的情况是：假如“人身上长的毛都是狗身上长的毛”真，可以推出“人是狗”真。实际情况是，“人身上长的毛都是狗身上长的毛”是假的（因为毛不可能同时长在人和狗身上），它不能推出“人是狗”真。因为，即使合乎推理规则，前提错，结论一定错。如果你能举个前提是真的句子，而合乎规则地推出假的结论，我才相信现有的逻辑力量。我总怀疑有些东西，现有的逻辑概括不了。

翟：前提：人的身上覆盖着的东西都是除人之外的动植物的身上覆盖的东西（按，实指衣服。但应该指出这个前提只在早期农业文明社会中是真的）。

结论：人是除人之外的动植物。

这大概是合乎你心意的例子了吧。由此例，你一定会更真切地感觉到，从该前提推导出该结论的规则（当然我不清楚这是什么样的规则，但这并不重要）一定是错的。因为你认可正确的规则能从真前提导致真结论，但现在却导致了假结论，因此规则一定是错的。

马：你举的例子固然好，但只是一种类型，与“马的毛是动物的毛”是不一样的。我们现在使用的逻辑是蕴涵式命题逻辑或讲普遍与特殊关系的词项逻辑。现在遇到的问题是，里面有个整体与部分的关系。“毛”是“马”的一部分，也是某个动物的一部分。这个关系，现在的逻辑怎么概括？你要是举反例，也应该是我讲的这个类型。

翟：我知道你的意思。你的区别在逻辑上是可以得到处理的。任何无毛的东西都不是马（毛是马的不可侵害的一部分），但却存在着不穿衣服的人（衣服不是人的不可分割的一部分），用符号化的语言表示就是：

(x)(如果x没有毛，那么x不是马），

（Ex）(x没有衣服而且x是人）。

三、马雷与杜国平的问答

马：我们能不能说“A∨B∨C 永真，当且仅当A∨B 永真或者A∨C 永真”？A、B、C 代表单一命题和代表复合命题对于这个论断有区别吗？

杜国平（以下简称“杜”）：

“A∨B∨C永真，当且仅当A∨B永真或者A∨C永真。”这是不正确的。举一例即可证明：p∨q∨非q 永真，但是p∨q 不永真，p∨非q 也不永真。A、B、C代表单一命题和代表复合命题对于这个论断没有区别。

马：你认为下面的推理对不对？

对于任何动物而言，它头上的毛一定有一个是动物的

马是动物

所以，对于任何马而言，它的头上的毛一定有一个是马的。

杜：这个推理可能应该问题不大，但是如果严格表述的话，最好是：

对于任何动物而言，如果它头上有毛，那么它头上的毛一定有一个是动物的；

马是动物；

所以，对于任何马而言，如果它头上有毛，那么它头上的毛一定有一个是马的

马：对于任何动物而言，如果它头上有毛，则它头上的毛一定有一个是动物的

马是动物

所以，对于任何马而言，如果它头上有毛，则它的头上的毛一定有一个是马的。

对于任何真的析取式而言，如果它有析取支，则它的析取支一定有一个是真的

永真是一种真

所以，对于任何永真的析取式而言，如果它有析取支，则它的析取支一定有一个是永真的。

后一个推理与前一个推理是一样的，为什么它的结论是错的？

杜：这个问题比较复杂。第一，“对于任何动物而言，如果它头上有毛，则它头上的毛一定有一个是动物的；马是动物；所以，对于任何马而言，如果它头上有毛，则它的头上的毛一定有一个是马的。”这是一个自然语言中的有效推理式。它的有效性还依赖于一些没有列出来的常识判断，例如“动物的头是动物的一个部分”等。这也是通常所说的预设。而后一个推理则纯粹是构造的，它是否有效只能根据纯粹的形式。第二，后一个推理的前提“永真是一种真”在逻辑上是不正确的，“真”是一个语义指派的情况，而“永真”是所有语义指派下的情况。

马：你说得有道理。但玉章证明下面的推理是有效推理。他证明错了吗？

对于任何动物而言，它的头上的毛是动物的

马是动物

所以，对于任何马而言，它的头上的毛是马的

“有效推理。从直观上就很清楚。但我还是将它推导如下。

两个前提和结论的同步结构是：

前提一：（x)(Fx→(Ey)(Gyx(Ez)(FzGyz)))

前提二：（x)(Hx→Fx)

结论：（x)(Hx→(Ey)(Gyx(Ez)(HzGyz)))

Fx:x是动物，Gxy:x是y头上的毛，Hx:x是马。

为了表明这是一个有效的推理，只需表明肯定前提而否定结论会导致矛盾即可。

1.（x）(Fx→(Ey)(Gyx(Ez)(FzGyz)))...前提一

2.（x）(Hx→Fx)...前提二

3.-（x）(Hx→(Ey)(Gyx(Ez)(HzGyz)))...结论的否定

4.（Ex）-(Hx→(Ey)(Gyx(Ez)(HzGyz)))...3的前置式

5.-（Ha→(Ey)(Gya(Ez)(HzGyz)))...4，特称例化

6.Ha-(Ey)(Gya(Ez)(HzGyz))...5，真值函项变换

7.Ha...6，合取的性质：如果合取为真，那么任一合取肢也为真。

9.-(Ey)(Gya(Ez)(HzGyz))...6，合取的性质

10.(y)-(Gya(Ez)(HzGyz))...9的前置式

11.Ha→Fa...2,全称例化

12.Fa...7,11,肯定前件推理

13.Fa→(Ey)(Gya(Ez)(FzGyz))...1,全称例化

14.(Ey)(Gya(Ez)(FzGyz))...12、13，肯定前件推理

15.Gba(Ez)(FzGbz)...14,特称例化

16.Gba...15,合取的性质：如果合取为真，那么任一合取肢为真。

17.-(Gba(Ez)(HzGbz))...10，全称例化

18.-Gba∨-(Ez)(HzGbz)...17，真值函项变换（德摩根定律）

19.-Gba∨(z)-(HzGbz))...18,移置律（将析取式后一个析取枝实现量词前置）

20.(z)(-HzGbz∨-Gba)...19,移置律（将整个析取式实现量词的前置）

21.-HaGba∨-Gba...20，全称例化

22.-Gba...21, 7，真值函项变换

23.Gba-Gba（矛盾）...22、16”

杜：1.你开始的问题是：“对于任何动物而言，如果它头上有毛，则它头上的毛一定有一个是动物的，马是动物，所以，对于任何马而言，如果它头上有毛，则它的头上的毛一定有一个是马的。”后来给出的证明是：“对于任何动物而言，它的头上的毛是动物的，马是动物，所以，对于任何马而言，它的头上的毛是马的。”这两者的表述是不同的。

2.“（x)(Fx→(Ey)(Gyx(Ez)(FzGyz)))”录入可能有误，缺少连接词⑩；

3.你给出的形式证明我不知道是哪里给出的，应该问题不大，但是已经对自然语言的意思进行了某些修正。证明应该没有什么问题。符号可能有误。

马：“马是动物”是否等值于“马的毛是动物的毛”？或“马的头上的毛是动物头上的毛”？

1.存在一根毛，如果它是动物头上的毛，则它是动物的毛

马头上的毛是动物头上的毛

所以，存在一根毛，如果它是马头上的毛，则它是动物的毛

2.存在一根毛，如果它是马头上的毛，则它是动物的毛

马的毛的动物的毛

所以，存在一根毛，如果它是马头上的毛，则它是马的毛

3.对所有毛而言，如果它是动物头上的毛，则它是动物的毛

马头上的毛是动物头上的毛

所以，对所有毛而言，如果它是马头上的毛，则它是动物的毛

4.对所有毛而言，如果它是马头上的毛，则它是动物的毛

马的毛是动物的毛

所以，对所有毛而言，如果它是马头上的毛，则它是马的毛

你认为这四个推理式都有效吗？

杜：“马是动物”肯定不等值于“马的毛是动物的毛”，也不等值于“马的头上的毛是动物头上的毛”。准确地说，这三者都相互不等值。

1.存在一根毛，如果它是动物头上的毛，则它是动物的毛

马头上的毛是动物头上的毛

所以，存在一根毛，如果它是马头上的毛，则它是动物的毛

有效。

2.存在一根毛，如果它是马头上的毛，则它是动物的毛

马的毛是动物的毛

所以，存在一根毛，如果它是马头上的毛，则它是马的毛

不有效。

3.对所有毛而言，如果它是动物头上的毛，则它是动物的毛

马头上的毛是动物头上的毛

所以，对所有毛而言，如果它是马头上的毛，则它是动物的毛

有效。

4.对所有毛而言，如果它是马头上的毛，则它是动物的毛

马的毛是动物的毛

所以，对所有毛而言，如果它是马头上的毛，则它是马的毛

不有效。

马：如果“马是动物”等值于“马的毛是动物的毛”，也等值于“马身上长的毛是动物身上长的毛”，则推理

动物的毛有一个是动物的

马是动物

所以，马的毛有一个是动物的

马的毛有一个是动物的

马是动物

所以，马的毛有一个是马的

就可以分别精确表达为

存在一根毛，如果它是动物头上的毛，则它是动物的毛

马头上的毛是动物头上的毛

所以，存在一根毛，如果它是马头上的毛，则它是动物的毛

（你认为有效）

存在一根毛，如果它是马头上的毛，则它是动物的毛

马的毛是动物的毛

所以，存在一根毛，如果它是马头上的毛，则它是马的毛

（你认为不有效）

这样就可以理解从“动物的毛有一个是动物的”推不出“马的毛有一个是马的”。

你说，“马是动物”肯定不等值于“马的毛是动物的毛”。你能不能找到反例？“马的毛是动物的毛”意思是说“马身上长的毛是动物身上长的毛”（区别与“马拥有的东西是动物拥有的东西”这个意思，比如“马的衣服是动物的衣服”）。一般认为，从“马是动物”能推出“马的毛是动物的毛”。但反过来为什么就不能？

杜：马的主人是牛的主人，但是马不是牛。

马：你这个反例太好了！但我说的是：X身上长的M是Y身上长的M，能不能推出X是Y？

杜：要反驳“X 身上长的M 是Y 身上长的M，推出X 是Y”，只需要举一个反例即可，不管这个反例多么特殊。

对于连体双胞胎（共用一只耳朵，记为A器官），X身上长的A器官是Y身上长的A器官，由此不能推出X是Y，因为X和Y是双胞胎，但不是一个人。

马：我疑惑的是，当一个东西同时长在所谓“两个”对象的身上时，其实这“两个”对象就不存在了，只能说是“一个”连接体。我们一般习惯于把连体双胞胎看成两个对象，其实只是一个连体胎。我们不能说“双头人”是两个人，也不能说不是两个人，只能说是一个连体人。正因为如此，这类人在身份认证、生活习惯、结婚生子等方面都与常人不同。如果是两个人，就不会出现这个情况了。

如果X 和Y 是一个对象或一类对象，从“X 身上长的M是Y身上长的M“可以推出“X是Y”。

注释：

①姓名以最先发出邮件的时间排序。就问答形式和内容而言，排名不分先后，每位问答者都应视为并列的第一作者。在问答和注释中，专家姓名以姓氏表示。

②翟后来通过邮件就黑体部分批注说：“回答非常好！”

③格·克劳斯著《形式逻辑导论》，金培文、康宏逵译，上海人民出版社1981年版。

④翟后来通过邮件就黑体部分批注说：“永真”和“真”确实是两个不同的概念。前者的适用对象是模式，可称为“永真式”（或有效模式）：一个模式是永真的，当且仅当该模式的所有替换例都是真的；后者适用对象是语句，可称为“真语句”，但真语句中有一类可称为永真句。我记得和你说过，“永真句”中的“永真”是个派生的概念：一个语句是永真的，当且仅当该语句是某个永真式的替换例。在奎因的书里，永真式和永真句分别被称为有效模式和逻辑真。奎因的术语是更好的。永真句这个概念有误导性，仿佛有些语句是永远真的，另一些语句则有时真有时假，但事实上，除了所谓场合句（比如“这里有许多人”）外，语句的真值是恒定的。

⑤翟后来通过邮件就黑体部分批注说：我上面的解说要比这清楚些。特别是，为了说清楚有效模式、逻辑真这些概念，无须节外生枝地使用有争议的“可能世界”概念。“可能世界”作为一个比喻的说法是很形象的，但却是一个不具解释力的概念，它比要解释的概念“逻辑真”来，并不更清楚些。（张又对此批注：玉章对“可能世界”的疑虑，可能是受奎因的影响。但多年研究已表明，“逻辑真理”至少不比“可能世界”更容易澄清，而我认为反过来倒更为可行。要解决条件句疑难等古老而常新的难题，是绕不开可能世界语义学的。）

⑥翟后来通过邮件就黑体部分批注说：我也反对王路的做法，但理由有所不同。在张看来王是把概念弄错了，而在我看来王是小题大做。真就是真理，两者的本意都是指真语句。“永真式”中的“真”是一个派生的概念：永真式就是所有替换例都为真语句的模式。（张又对此批注：王路的出发点是区分认识论的truth 概念和语义学的truth 概念，这是有道理的；然而，这种区分应是对同一种对象的不同把握，否则就难以说清语义学对认识论的贡献了。从经典语义学看，truth 有无穷多，而真值只有两个真与假；truth 就是“为真的东西”，若直接译为“真语句”“真命题”或“真陈述”，那都是假定了一种关于真值载体的哲学观点，故还是译为“真理”为好。）

⑦翟后来通过邮件就黑体部分批注说：条件式。当然，每一个条件句都对应一个实质蕴含句。而逻辑真的条件句则对应一个严格蕴含句。

⑧张后来通过邮件针对这一点发表如下看法：有一个地方请注意，你在与玉章的讨论中说：符合推理规则的推理，就是如果前提真，并且符合推理规则，结论一定真；如果前提假，并且符合推理规则，则结论必然假。

其中分号后的一句话要去掉，前提假、符合推理规则，结论真的事例很多；有效演绎前提到结论保真，但并不保假。

玉章说要区分条件句和蕴涵句，这是很有启发的；条件句和蕴涵句同义在学界约定俗成，但这种用法的确造成了很多问题。

我今年在《学术研究》发表了一篇关于蕴涵问题的论文，因涉及量化，可能对你的著作中有关问题的研究有用，寄上供参考。蕴涵问题我考虑了整30年，终于在2010年彻底想通，最近要发系列论文。这是应《学术研究》约稿写的第一篇。（指《从形式蕴涵看“实质蕴涵怪论”》，载《学术研究》2012年第4期——马雷注）

⑨翟后来通过邮件就黑体部分作出评注：严格说来，这里对假定条件的概括是错误的。正确的概括是：人身上植入的毛（曾经）是狗身上长的毛。但这样一来，这就不再是一个反例了。我举的另外两例确实是反例，但相比而言，杜在和你的对话中所举的反例才是一个既直观又自然的好例子。

⑩翟后来通过邮件就黑体部分作出批注：就像代数中的乘法符号可以被省略一样。同样，在逻辑中，合取的符号也可被省略。这个式子相当于：（x)(Fx→（Ey)(Gyx∧(Ez)(Fz∧Gyz)))