铸造凝固界面换热系数求解的反热传导模型
2014-12-15张立强李落星谭文芳
张立强,李落星,谭文芳,徐 戎
(1.中南林业科技大学 机电工程学院,长沙 410004;2.湖南大学 汽车车身先进设计与制造国家重点实验室,长沙 410082)
在铸造领域中,随着计算机模拟技术的不断进步和完善,提高铸造过程模拟的精确性就成为诸多研究工作者需要解决的关键问题之一[1-2]。如果要改进铸造数值模拟精确性,首先必须知道作为数值模拟重要边界条件之一的界面换热系数在铸造凝固过程中是如何变化的,特别对于金属型铸造,因为冷却速度较砂型铸造要快得多,界面传热行为的研究对数值模拟结果的精确性更加重要[3]。然而,界面换热系数并不能简单地通过实验或理论的方法来确定或求解。目前,求解铸件-铸型界面换热系数最常用的技术是反热传导方法。在已有反热传导方法的基础上,BECK等[4-5]针对反热导的特殊情况做了很多改进,例如反热传导方法研究者所熟悉的未来时间步长在反传热计算中的应用,大大提高了反求结果的稳定性和计算精度。之后,有更多的研究者将反热传导技术发展并广泛地应用在各种换热条件反求过程中,包括铸件-铸型间换热系数的估算[6]、铸件急冷过程中界面热流的计算[7]以及对流换热系数的求解[8]等。
虽然目前反热传导方法被作为一个主要的方法来求解和研究铸件和铸型间的换热行为,但大部分文献中采用的反热传导方法来计算换热系数时都是基于铸型内实验测量的温度数据[9-11],而通过铸件内测量采集的温度数据来计算界面换热系数的研究较少。这是因为在利用反热传导方法计算换热系数时,需要多次迭代计算正传热过程,而如果以铸件内实验测量的温度数据作为已知条件来求解界面换热系数时,正传热过程计算时不得不考虑铸件凝固过程中潜热的释放,这样使得反求计算非线性,计算过程变得更加繁杂,甚至程序计算不收敛[12]。PRABHU等[13]使用反热传导技术结合有效比热法来求解铝合金单向凝固过程中界面系数并研究了钠变质处理对铸件与铸型换热系数的影响,但文献中对于应用的方法并没有做详细的介绍。另有部分研究者采用其他反求法来通过铸件内测量的温度来反算界面换热系数,例如MARTORANO等[14]使用全域法来反算求解考虑潜热释放的热传导差分方程,SUN等[15]为反计算界面换热系数提出了集总热容法来处理潜热,并成功地应用在砂型铸造过程中铸件与铸型间换热系数的研究方面。
基于以上分析,本文作者以 A356铝合金为铸件材料,建立了基于等效比热法的反热传导模型,通过分析模型中反算参数对界面换热系数计算结果的影响,来提高求解结果的稳定性及准确性,并基于铸件内温度数据成功地应用此模型求解分析了 A356铝合金与铜冷却介质间的界面换热系数随凝固时间的变化规律。
1 数学模型
1.1 一维正传热模型
采用反热传导法计算求解铸件/铸型界面换热系数,需要不断地迭代计算正传热温度场。因此,正传热问题的反复求解过程如果是三维的,计算工作量相当大,为了减小计算量,一般可以将铸件/铸型界面换热系数的求解过程简化为一维问题处理[11]。
一维正传热问题的求解是指在初始条件和边界条件已知的情况下,通过热传导方程来计算求解域内的温度场,正传热的热传导方程表达式如下[15]:

式中:ρ、cp、k分别是材料的密度(kg/m3)、定压比热容(kJ/(kg·K))和导热系数(W/(m·K));T是温度(K);t为时间(s);Q是与凝固潜热释放有关的内热源(W/m3)。
1.2 一维反热传导模型
反热传导问题与正传热问题相反,反热传导算法的求解过程是通过铸件或铸型内部已知的温度场来反求未知的边界条件。反热传导算法的求解过程中,根据BECK等[4]的非线性系列估算法可以将随时间变化的热流q(t)分成若干个时间间隔的离散值(qi=q1,q2,…,qN),如图1(a)所示。另外,由于铸件或铸型内部热电偶温度的响应滞后于铸件/铸型界面的温度变化,因此在求解每个Δθ时间间隔内的热流qi时,假设qi在RΔθ时间间隔内为一个常数,R为未来时间步长,如图1(b)所示,未来时间步长R的正确选择有助于改善反算法的稳定性。
采用反热传导算法求解界面热流时,需要设置相应的计算参数,这些参数主要包括:未来时间步长R、热流计算的时间步长Δθ、迭代收敛误差判据、初始温度场以及初始设定的热流等。这些设置完成之后,开始反算求解,基本的反热传导算法的流程图如图2所示。当第一个Δθ时间间隔内的热流q1通过迭代计算得到后,循环计算下一个Δθ时间间隔内的热流q2,周而复始,直到每个Δθ时间间隔内的热流qi全部计算得到为止。其中每个Δθ的热流qi是通过测量温度与计算温度误差值最小的判据迭代计算获得,可用式(2)表示:
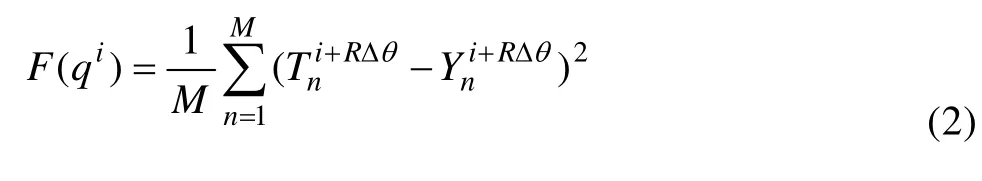
式中:M是求解的未知热流数;Tni+RΔθ为在i+RΔθ时间内基于qi的计算温度;Yni+RΔθ是在i+RΔθ时间内的测量温度;函数F是通过迭代计算的目标函数。在每次迭代求解热流qi过程中,Δq通过下式计算:

式中:S是敏感系数,被定义为在铸件或铸型内某位置温度随着单位热流变化的响应,它可以通过数值差分的方法近似计算得到,其表达式如下:
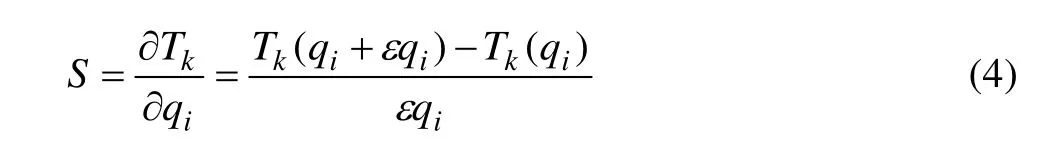
式中:i=1,2,…,N;k=1,2,…,P;ε是一个数值差分计算采用的很小值,在此取为0.001。
在迭代计算热流时,通过一个迭代值Δq更新qi,一个接近1值的阻尼系数μ被使用来稳定计算结果,迭代计算方程如下:

当式(2)中测量的温度与计算的温度差值满足给定的收敛误差值时,如|ΔTi+RΔθ|≤Tcr,当前时间步长的qi可以被反计算得到。然后,将此时得到的界面热流值作为计算下一时刻热流值qi+1时的初始假设值,重复上面的过程,直到所有时刻内的热流q(t)被计算得到为止。
1.3 合金潜热处理
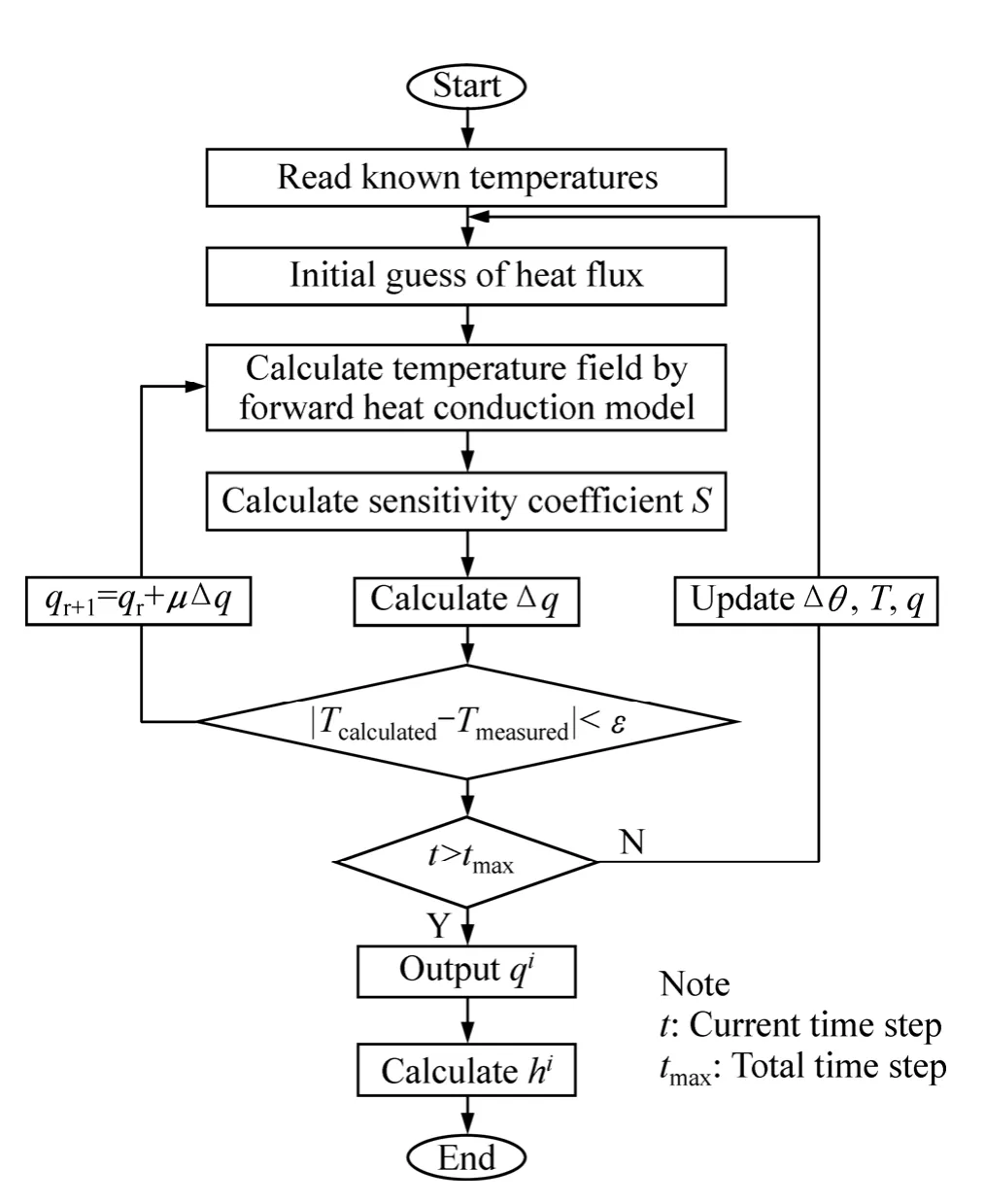
图2 反热传导算法流程图Fig.2 Flow chart of inverse heat conduction algorithm
铸造凝固时铸件由液相转变为固相并伴随结晶潜热释放,其潜热释放会使正热传导数值计算变得更加复杂,甚至导致计算的温度场结果不稳定。因此,在铸造凝固数值模拟计算时必须考虑结晶潜热释放的过程,有效比热法是将结晶潜热折算成比热容加到合金的实际比热上,作为合金结晶温度区间的修正比热容,是应用较为广泛的结晶潜热处理方法之一。在本模拟中,在处理结晶潜热时,在有效比热法的基础上再次采用等效比热法计算铸件凝固过程中的潜热释放。
应用有效比热法处理凝固过程中释放的潜热,包含内热源的热传导方程式(1)可以等效地表示为[16]
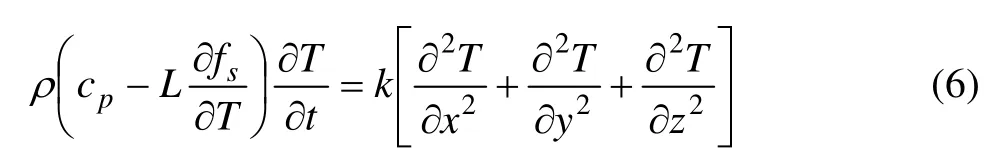
式中:L是铸件材料的凝固潜热(J/kg),fs是固相体积分数,是有效定压比热容(kJ/(kg·K))。铸件凝固过程中实际释放的潜热等于在Ts和Tl之间有效比热所包围的面积[17],如图3所示,Ts和Tl分别铸件材料的固相温度和液相温度。因此,式(6)中的有效比热可以用与有效比热法曲线下积分面积相等的等效比热法来处理,如图3所示。等效比热法的优点是在热传导数值计算过程中忽略了潜热释放有关的峰值,从而提高计算过程中的稳定性。
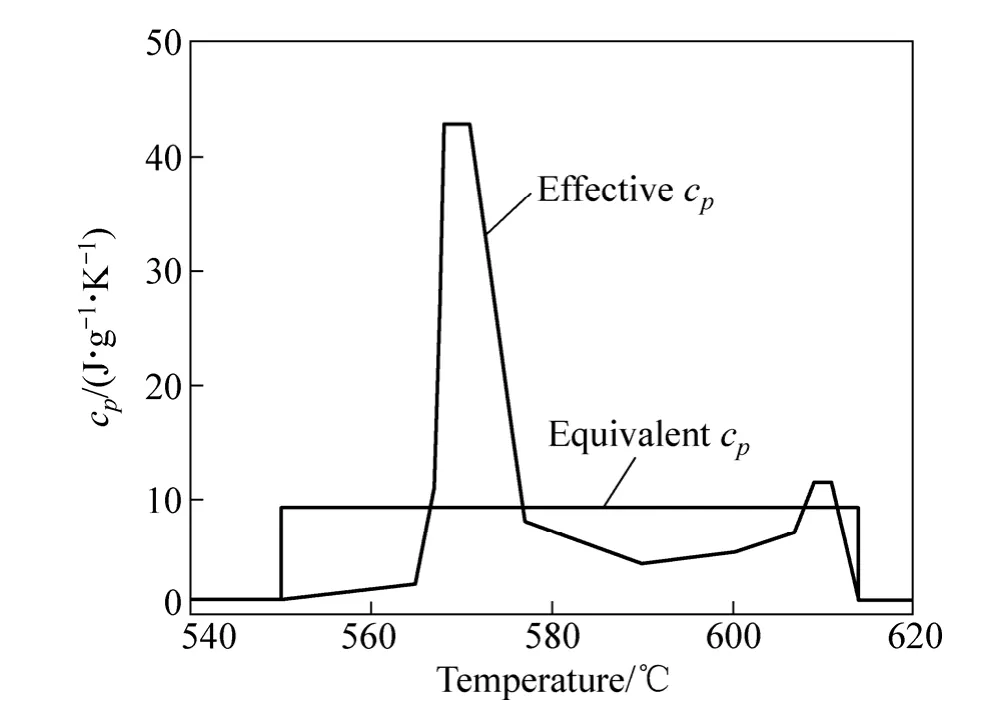
图3 随温度变化的有效比热容和等效比热容Fig.3 Effective and equivalent specific heat capacities variation with temperature
2 反热传模型讨论与分析
为验证建立的反热传导模型计算换热系数的准确性和有效性,首先假设界面换热系数已知并且是随时间变化的h(t),如图4所示。通过已知的初始条件和界面换热系数等边界条件可以采用正传热数值方法计算得到研究体的温度场,然后将计算得到的研究体内温度场作为已知条件通过建立的反热传导模型来反求界面换热系数,再对比之前假设的值来验证反热传导模型的准确性。
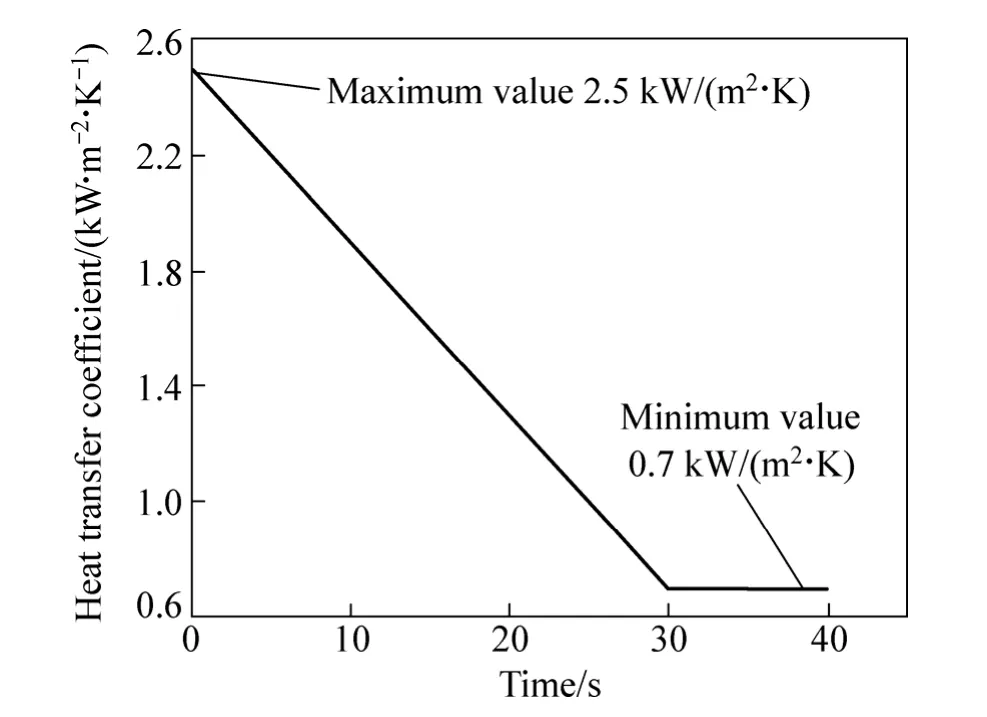
图4 假设的随时间变化的界面换热系数Fig.4 Assumed heat transfer coefficient variation of interface with time
图5所示为反求计算得到的界面换热系数随时间的变化情况以及反算参数如μ值对其计算结果的影响。从图5(a)可以看到,在大约前10 s内,μ值对反热传导模型计算结果影响较大,而在10 s之后,影响很小,可以忽略不计。从图5(b)可以更加清楚地知道,当计算μ值接近1时,反算结果更加稳定。
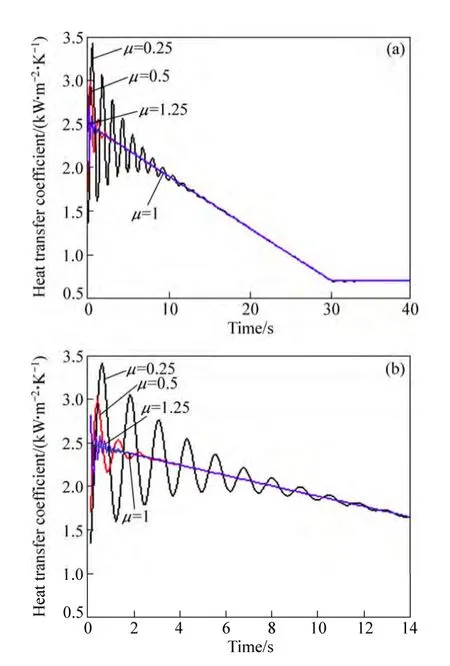
图5 μ值对界面换热系数反算结果的影响Fig.5 Variation of calculated heat transfer coefficient with different values of μ: (a) 0-40 s; (b) 0-14 s
图6所示为未来时间步长R和正传热数值计算时间步长 Δθ对反热传导模型计算结果的影响。从图6中可以看出,当μ值为1,R和Δθ分别为5和0.1 s时,反算的结果最稳定。此外,图6还反映出当μ值和R值相同时,Δθ为0.1 s比0.05 s时的计算结果更好,这说明不是正传热计算时间步长越小越好。而当μ值和Δθ值相同时,未来时间步长R为5时的计算结果更好,说明反热传导计算过程中的参数正确选取对于计算结果的稳定性和准确性影响很大。
图7所示为收敛误差值Tcr对界面换热系数反算结果的影响。从图7可以看到,其他参数μ值和R值保持不变时,随着收敛误差值Tcr的减小,计算结果更加稳定。然而在实际反算过程中,收敛误差值Tcr不能太小,如果太小,会增加迭代收敛的步数,从而增加了计算工作量。
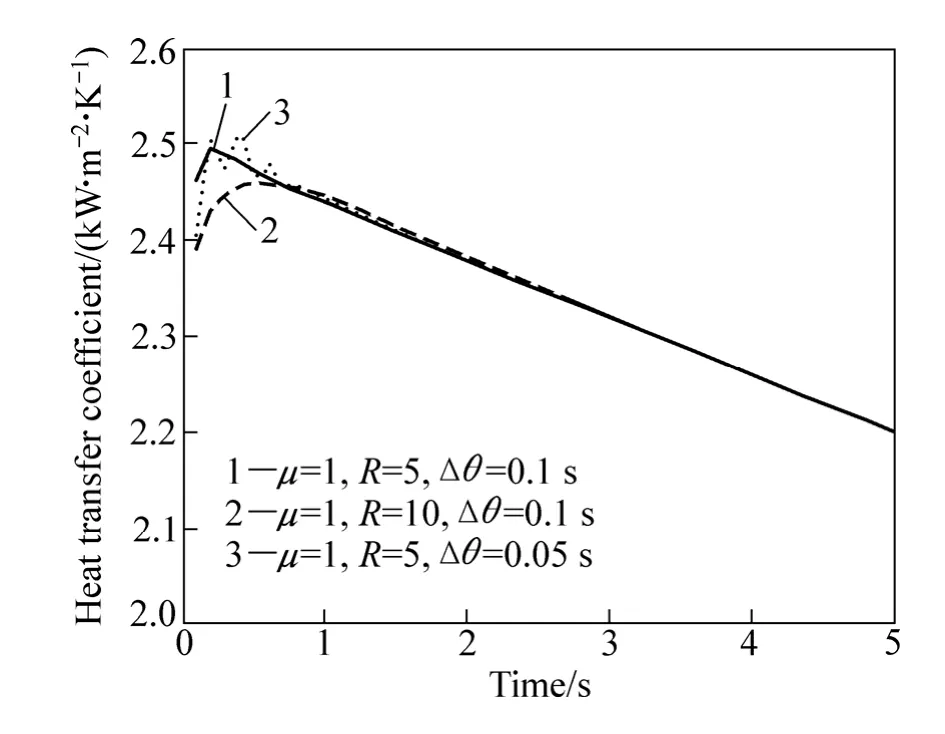
图6 未来时间R值和正传热时间步长Δθ对界面换热系数反算结果的影响Fig.6 Effect of number of future time step R and time step Δθ on calculated heat transfer coefficient
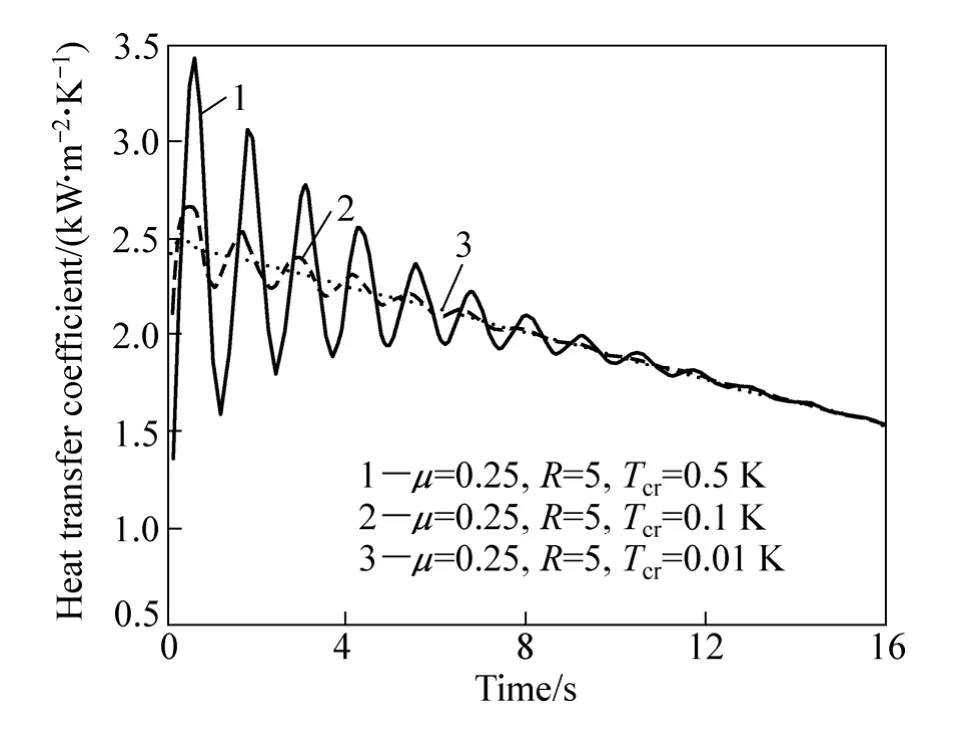
图7 收敛误差值Tcr对界面换热系数反算结果的影响Fig.7 Effect of tolerance criteria Tcr on calculated heat transfer coefficient
通过上面的讨论与分析可以知道,在应用反热传导模型计算界面换热系数时,反算过程中的计算参数未来时间步长R和收敛误差值Tcr等对计算结果影响很大,因此,为提高计算结果的准确性和稳定性,在应用反热传导模型求解界面换热系数前需要针对具体研究体的情况对反算的各种参数进行优化选择。另一方面,比较计算的和初始假设的界面换热系数,可以知道,在合适的反算参数下,通过本文作者提出的反热传导模型可以准确地求解界面换热系数。
3 应用实例
为验证所建立的一维反热传导模型,针对设计的一维传热过程,利用建立的反热传导模型对A356铝合金铸件与金属冷却介质间的界面换热系数进行求解。
3.1 实验设计
为利用反热传导方法来求解铸件与金属冷却介质间的界面换热系数,采用单向铸造凝固实验得到的温度数据,实验过程示意图如图8所示。图中T1、T2和T3是热电偶的放置的3个位置,分别距离金属冷却介质表面2、5和10 mm,测温用热电偶为直径为0.2 mm的K型热电偶,一端由2.3 mm的陶瓷管保护后插入铸件型腔内,另一端通过USB-2416温度数据采集仪连接电脑,温度数据采集频率为50 Hz。为保证实验过程中热量的单向传递,耐热模具外表面通过放置耐热石棉进一步减少铸件凝固冷却过程中铸件与外界环境间的热交换。同时,金属冷却介质里设置冷却水道来加快实验过程中铸件单向的热量传递,实验过程中的实际水流量是0.4 L/s。实验中使用的铸件材料是A356铝合金,铝合金放置在石墨坩埚内通过感应电炉加热熔化达到750℃后浇注到耐热铸型中,整个浇注时间大约持续9 s。
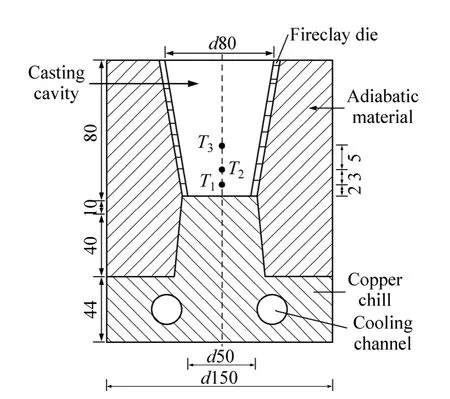
图8 实验过程示意图Fig.8 Schematic diagram of experimental setup (Unit: mm)
3.2 界面换热系数计算结果
采用反热传导算法求解界面换热系数时,首先通过铸件或铸型内部已知的温度场来计算界面的热流,当界面热流已知,可再一次求解正传热问题分别得到铸件与铸型的表面温度,再通过式(7)计算界面换热系数。

式中:h是界面换热系数(W/(m2·K)),q是界面热流(W/m2),Tcasting和Tchill分别是铸件与铸型的表面温度(K)。在此采用靠近界面2 mm位置T1的温度数据作为已知的温度场来计算界面换热系数,将距离界面5 mm位置T2和10 mm位置T3的温度数据用作反算结果的验证。图9所示为反热传导模型计算的铸件与水冷金属冷却介质间的界面换热系数和界面温度随时间变化的曲线,界面温度是应用反算所获取的界面换热系数通过正热传导数值计算而得到的。从图9可以看出,在铸件冷却凝固的开始阶段,界面换热系数快速增加到6 216 W/(m2·K)的最大峰值,当界面温度下降到固相线附近时达到3 856 W/(m2·K)的第二个峰值,而在固相线以下时保持一个常数约1 200 W/(m2·K)不变。界面换热系数的最大和最小值相比文献[18]中报道的钢冷却介质的结果要高,这是因为铜冷却介质的热传导性更好。
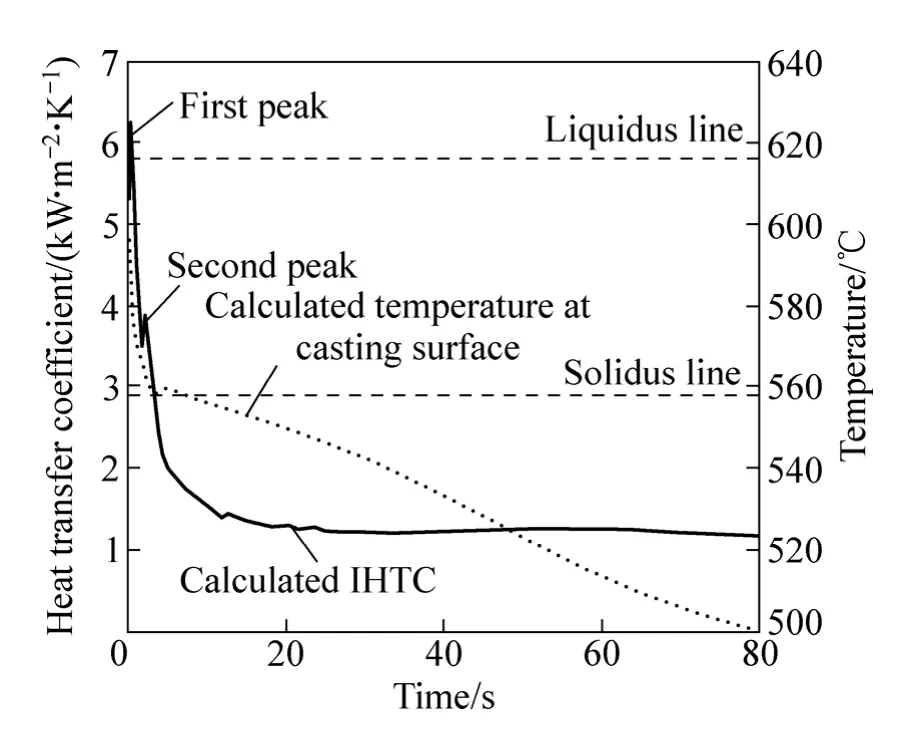
图9 计算的界面换热系数与界面温度随时间的变化Fig.9 Variation of identified IHTC and calculated temperature at casting surface with time
在铸件凝固的开始阶段,界面换热系数快速增加到如图9所示的最大值,这是由于铜冷却介质与液态金属的表面充分接触。铸件凝固过程中的冷却速度主要由铸件与金属冷却介质间的接触状态及冷却介质的热传导率决定,在凝固的开始阶段,液态金属与铜冷却介质表面接触最充分,铸件与金属冷却介质间的热交换主要是以热传导的方式进行,此时,界面换热系数最大。在约2 s时,界面换热系数降至一个最小值,随后到达第二个峰值,根据文献[15]的报道,此峰值是由于A356铝合金发生共晶凝固而放出的潜热,导致界面热流有一个小的波动。此外,从图9可以知道,当界面换热系数到达第二个峰值时,铸件表面温度大约是700℃,这也与文献[19]报道的发生共晶凝固的开始温度相一致。在约15 s时,铸件表面温度下降到固相温度以下,界面换热系数基本上保持一个常数不变。此时,铸件凝固过程已全部完成,凝固时的体积收缩也相应地结束,铸件与金属冷却介质间形成了稳定地接触状态,致使界面间传递的热量稳定,从而导致界面换热系数不变。另一方面,在铸件材料完全凝固之后,其热传导率也大致上不再随温度变化,这也可能是界面换热系数不再变化的另外一个主要原因。
在图9中界面换热系数到达两个峰值后而继续下降的原因是铸件凝固过程中与铜冷却介质间形成了空气层间隙[20],如图10所示。界面间隙主要是铸件凝固时的体积收缩造成的,当微小地间隙在界面形成后,铸件与金属冷却介质不再紧密地接触,此时,界面的热交换主要以对流、辐射及间隙里气体的热传导3种形式组成,热交换过程变得非常复杂,铸件或模具的热传导性、铸件和模具的厚度及模具表面粗糙程度等许多因素都可能会影响到界面换热系数的变化[9-10]。
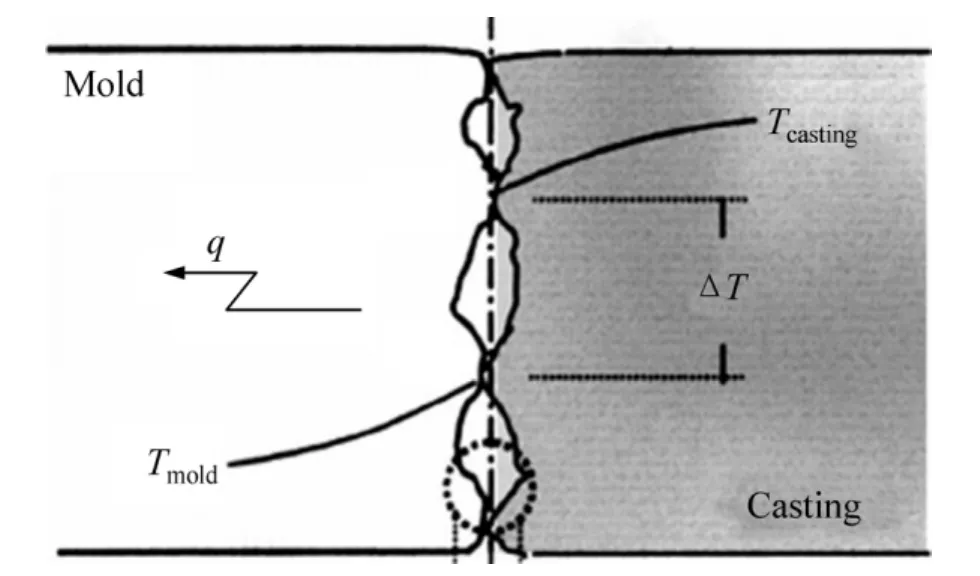
图10 铸件/铸型间的热流变化示意图Fig.10 Schematic diagram of heat flux change at casting/mold interface
3.3 测量误差分析
铸造凝固测温实验时,主要的测量误差是热电偶由于延迟效应带来的测温误差。接触法测温的基本原理是测温元件要与被测对象达到热平衡,因此,在测温时需要保持一定时间,才能使两者达到热平衡,当铸件或模具温度场变化时,热电偶的温度响应值并不是与实际温度场同步,而是有一定的滞后时间,从而给测量带来误差。而保持时间的长短,与测温热电偶的热响应时间有关,热电偶的测量端直径也是其主要因素,即热电偶丝越细,测量端直径越小,其热响应时间越短。根据文献[21]可知,K型热电偶因为延迟效应最大测温误差(Δθ)满足以下关系:

式中:α为K型热电偶镍鉻-镍硅的导热系数,其值为3.28×10-3mm2/ms,β为所测温度的变化率。在本实验中,采用直径为0.2 mm的K型热电偶,焊接后测温端形成球状,其半径R最大不超过0.2 mm,通过式(8)计算得到最大响应时间为2 ms,则最大测温误差为0.014 6 K。本文作者在应用反模型求解界面换 热系数时,分别对不同测温误差对界面热流计算的结果进行分析,其结果如图11所示,由图11可以看出,当测温误差大于1 K时,计算结果的误差较大;而当测量误差小于0.1 K时,计算误差并不明显。因此,本研究过程中的最大测温误差较小为0.014 6 K,在界面换热系数求解过程中可以忽略不计。
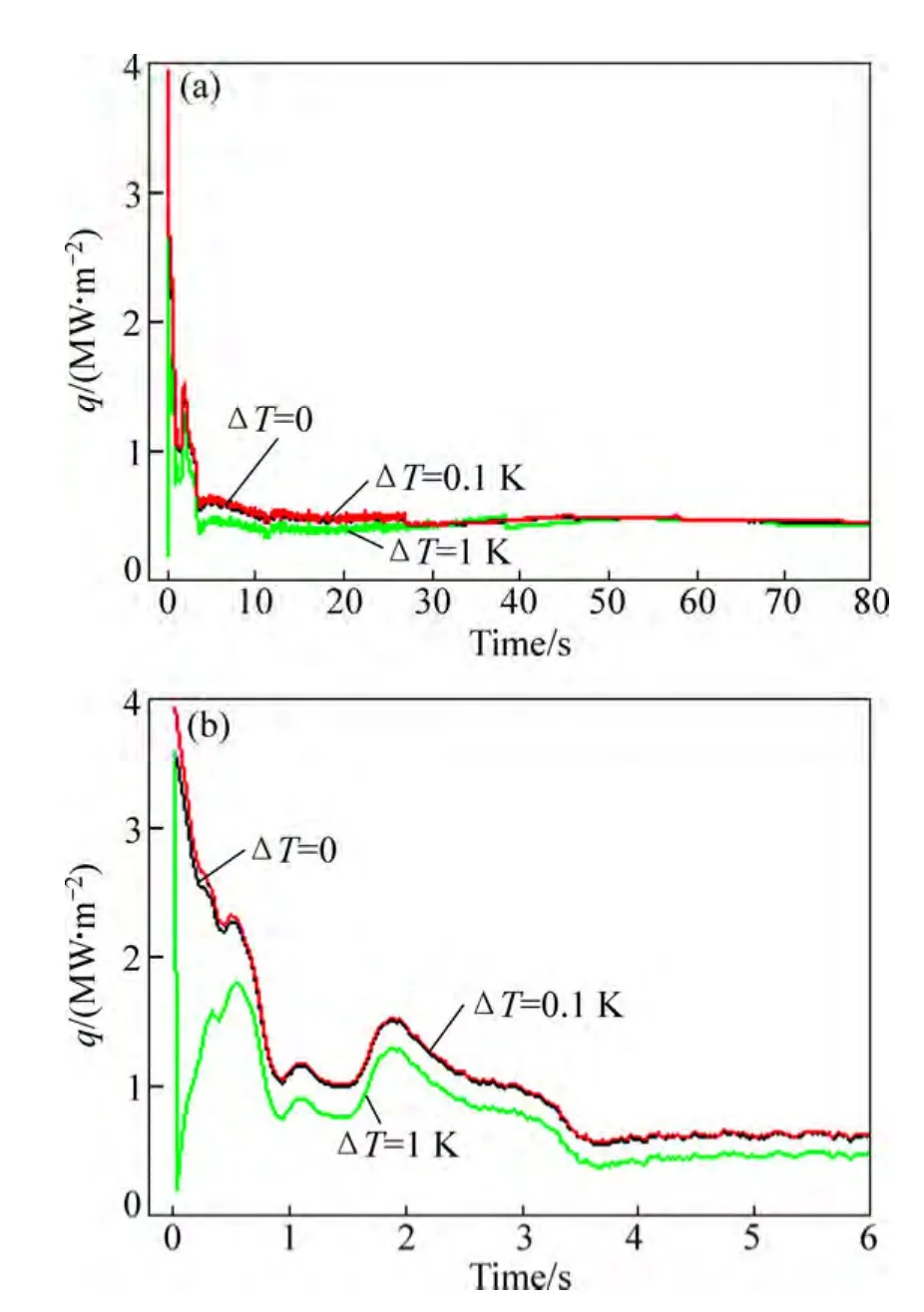
图11 不同测温误差对界面热流计算结果的影响Fig.11 Effect of temperature measurement error on interfacial heat flux: (a) 0-80 s; (b) 0-6 s
铸造凝固测温实验时,测温误差是不可能避免的,除热电偶由于延迟效应带来的误差外,还有热电偶本身的误差及安装位置波动带来的误差等。为了减小测量误差的影响,在本研究过程中,通过尽可能将热电偶放置在离界面较近的位置、采用陶瓷管固定热电偶的方式、选取较小的直径为0.2 mm的热电偶丝以及在反算模型中增加将来时间步长参数等办法,尽可能减小位置波动带来的误差以及热电偶延迟效应带来的测量误差。
3.4 反算的界面换热系数结果证实
由上面的讨论可知,铸件内部距离界面5 mm位置T2和10 mm位置T3的温度数据用来验证反算得到的界面换热系数。图12所示为实验测量温度与数值计算温度结果的比较,数值温度数据是通过应用反算的界面换热系数求解正热传导模型得到的。从图12中可以看到,计算的温度结果与实验测量温度相吻合,距离界面 5 mm位置温度相比较的最大误差低于6 K(0.9%的相对误差),距离界面10 mm位置温度的最大误差低于4 K (0.7%的相对误差)。计算温度与实验测量温度间误差可能是在实验过程中,热电偶测量位置的误差造成的。因为放置热电偶时热电偶间的相互干扰,热电偶很难准确地放置在中心线上,而实际热传导数值计算过程中,又假设热电偶是放置在中心线上,这样就会产生温度测量的误差,这可能是计算温度与测温度温度误差的主要原因。另外,在正热传导数值计算时采用等效比热法也会产生计算误差,这也可能会造成计算温度与测量温度的差异。然而,根据文献[18],数值计算的温度与测量温度误差小于20 K都是可以接受的,因此,温度比较的结果表明采用反热传导方法计算铸件凝固过程中铸件与金属冷却介质间的界面换热系数是准确和可靠的。
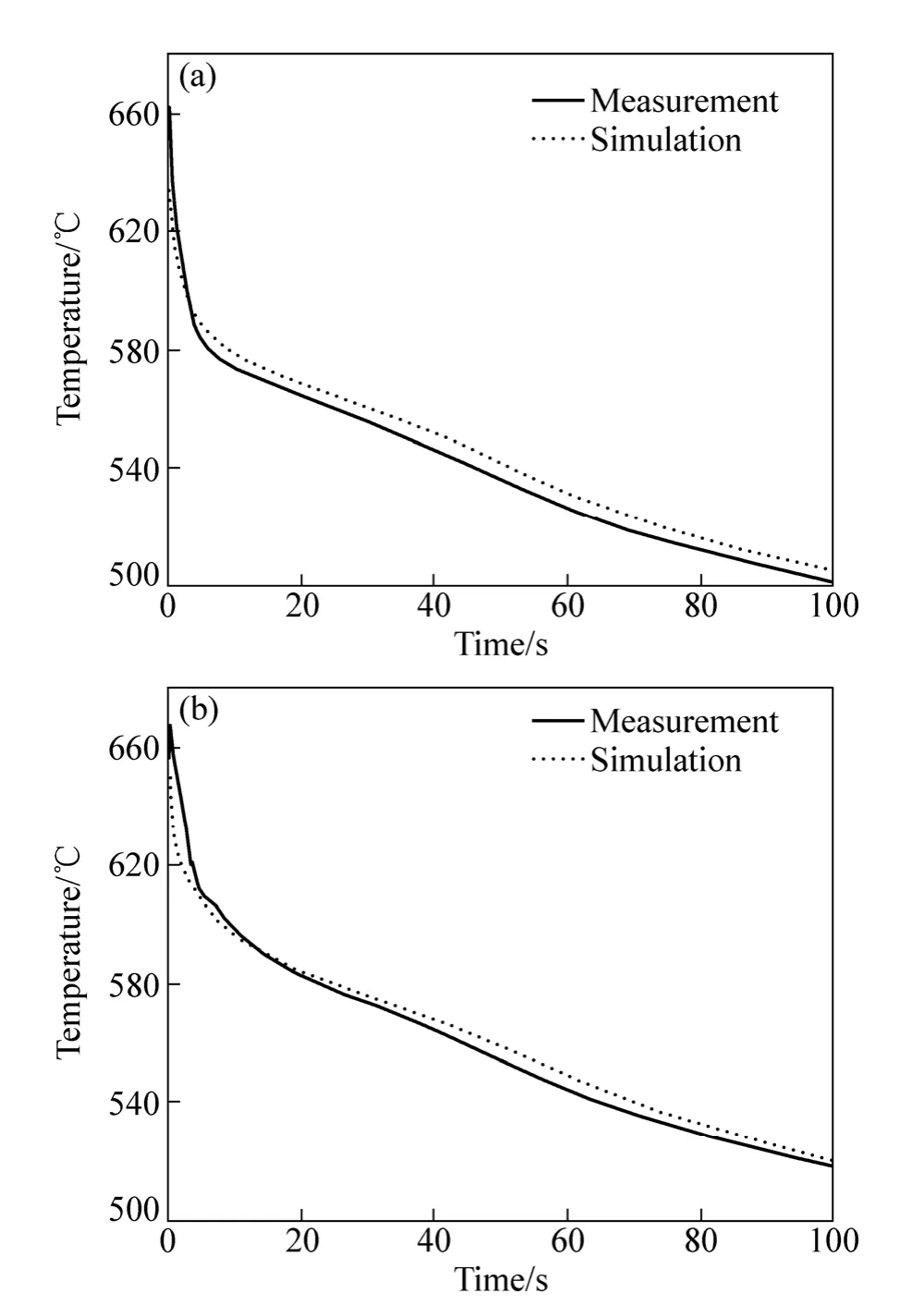
图12 测量温度与计算温度的比较Fig.12 Comparison of simulated and measured temperatures:(a) At location of 5 mm from interface; (b) At location of 10 mm from interface
4 结论
1) 在应用反热传导算法求解铸件与铸型界面换热系数时,阻尼系数μ、未来时间步长R、正热传导计算时的时间步长Δθ及收敛误差值Tcr等计算参数对反算求解结果的稳定性及准确性影响很大,因此,在反热传导模型应用前,为保证计算精度,需要分析选取合理的参数。
2) 建立了基于等效比热法的反热传导模型,应有此模型计算得到了A356铝合金与铜冷却介质间的界面换热系数,结果表明界面换热系数是随铸件凝固时间变化的,变化范围在1 200~6 200 W/(m2·K)之间,而且界面换热系数在变化过程中因为结晶潜热的释放存在两个峰值。
3) 计算温度和实验测量温度结果相吻合,而且最大误差低于6 K,验证结果证实了本文作者建立的反热传导模型求解铸件与金属冷却介质间界面换热系数的准确性和可靠性。
[1]WU S P, LI C Y, GUO J J.Numerical simulation and experimental investigation of two filling methods in vertical centrifugal casting[J].Transactions of Nonferrous Metals Society of China, 2006, 16(5): 1035-1040.
[2]JALURIA Y.Challenges in the accurate numerical simulation of practical thermal processes and systems[J].International Journal of Numerical Methods for Heat & Fluid Flow, 2013, 23:158-175.
[3]杜凤山, 张 沛, 许志强, 赵玲玲.铝铸锭凝固边界热交换规律及温度场模拟[J].中国有色金属学报, 2007, 17(11):1750-1754.DU Feng-shan, ZHANG Pei, XU Zhi-qiang, ZHAO Ling-ling.Law of heat transfer and simulation of temperature field for aluminum ingot solidification[J].The Chinese Journal of Nonferrous Metals, 2007, 17(11): 1750-1754.
[4]BECK J V, BLACKWELL B, CLAIR C.Inverse heat conduction: Ill-posed problems[M].London: Wiley, 1985: 2-50.
[5]BECK J V, WOODBURY K A.Inverse problems and parameter estimation: Integration of measurements and analysis[J].Measurement Science & Technology, 1998, 9: 839-847.
[6]徐 宏, 侯 华, 赵宇宏, 陈 铮.铝铸件凝固模拟边界热交换系数的测定[J].中国有色金属学报, 2003, 13(4): 881-886.XU Hong, HOU Hua, ZHAO YU-hong, CHEN Zheng.Determination of boundary heat-transfer coefficient for casting solidification simulation[J].The Chinese Journal of Nonferrous Metals, 2003, 13(4): 881-886.
[7]NOWAK I, SMOLKA J, NOWAK A J.An effective 3-D inverse procedure to retrieve cooling conditions in an aluminium alloy continuous casting problem[J].Applied Thermal Engineering,2010, 30: 1140-1151.
[8]CHEN W L, YANG Y C, LEE H L.Inverse problem in determining convection heat transfer coefficient of an annular fin[J].Energy Conversion and Management, 2007, 48:1081-1088.
[9]GAFUR M A, NASRUL H M, NARAYAN P K.Effect of chill thickness and superheat on casting-chill interfacial heat transfer during solidification of commercially pure aluminium[J].Journal of Materials Processing Technology, 2003, 133: 257-265.
[10]ZHANG L Q, LI L X.Determination of heat transfer coefficient at metal/chill interface in the casting solidification process[J].Heat and Mass Transfer, 2013, 49: 1071-1080.
[11]郭志鹏, 熊守美, 曹尚铉, 崔正吉.铝合金压铸过程铸件/铸型界面换热行为的研究[J].金属学报, 2007, 43(11):1149-1154.GUO Zhi-peng, XIONG Shou-mei, CHAO Sang-hyun, CHOI Jeong-kil.Study on heat transfer behavior at metal/die interface in aluminum alloy die casting process[J].Acta Metallurgica Sinica, 2007, 43(11): 1149-1154.
[12]TIKHONOV A N, ARSENIN V Y.Solution of ill-posed problem[M].New York: Wiley, 1977: 2-10.
[13]PRABHU K N, RAVISHANKAR B N.Effect of modification melt treatment on casting/chill interfacial heat transfer and electrical conductivity of Al-13% Si alloy[J].Materials Science and Engineering A, 2003, 360: 293-298.
[14]MARTORANO M A, CAPOCCHI J D T.Heat transfer coefficient at the metal-mold interface in the unidirectional solidification of Cu-8%Sn alloys[J].International Journal of Heat and Mass Transfer, 2000, 43: 2541-2552.
[15]SUN H C, CHAO L S.Analysis of interfacial heat transfer coefficient of green sand mold casting for aluminum and tin-lead alloys by using a lump capacitance method[J].Journal of Heat Transfer, 2007, 129: 595-600.
[16]QI L H, LIU J, GUAN J T, SU L ZH, ZHOU J M.Damage prediction for magnesium matrix composites formed by liquid-solid extrusion process based on finite element simulation[J].Transactions of Nonferrous Metals Society of China, 2010, 20(9): 1737-1742.
[17]YAO S, GONG X N, DAI L X, MA CH Y, JIN J Z, ABULITI A.The mathematical model of solidification latent heat under high cooling rate[J].Journal of Heat Transfer, 2006, 35(2): 115-121.
[18]ŞAHIN H M, KOCATEPE K, KAYIKCI R, AKAR N.Determination of unidirectional heat transfer coefficient during unsteady-state solidification at metal casting-chill interface[J].Energy Conversion and Management, 2006, 47: 19-34.
[19]THOMPSON S, COCKCROFT S L, WELLS M A.Advanced light metals casting development: Solidification of aluminum alloy A356[J].Materials Science and Technology, 2004, 20:194-200.
[20]ILKHCHY A F, JABBARI M, DAVAMI P.Effect of pressure on heat transfer coefficient at the metal/mold interface of A356 aluminum alloy[J].International Communications in Heat and Mass Transfer, 2012, 39: 705-712.
[21]魏可臻, 张 奇.热电偶热传导测温中的动态响应时间和误差估计[J].测试技术学报, 2007, 21(6): 523-526.WEI Ke-zhen, ZHANG Qi.Dynamic response time and deviation estimate of thermocouple during heat-exchange temperature measurement[J].Journal of Test and Measurement Technology, 2007, 21(6): 523-526.
