侧向侵蚀相关的走滑断裂滑动速率计算新方法

任治坤 张竹琪 陈 涛 王伟涛

1)中国地震局地质研究所，地震动力学国家重点实验室，北京 100029

2)中国地震局地壳运动监测工程研究中心，北京 100036

0 引言

活动构造研究中最主要的内容之一就是断层滑动速率的确定，滑动速率是量化断层活动性的重要参数，可以为地震危险性评价、震灾防御和建筑物设防级别等提供参考。断层滑动速率还是研究地壳变形的重要参数之一，比如对青藏高原的研究，研究者根据各自得到的不同的断层滑动速率，提出了不同的变形模式:在主要边界断层上获得低滑动速率的研究者大多支持连续变形模式(Molnar et al.，1975;England et al.，1988;Zhang et al.，2004);而在主要边界断层上获得较高滑动速率的研究者大多支持刚性块体变形模式(Peltzer et al.，1988;Tapponnier et al.，2001a)。早期研究显示，青藏高原地区主要活动断裂上的滑动速率达到20～30 mm/a(Peltzer et al.，1989;van der Woerd et al.，2002;Mériaux et al.，2004，2005)，从而认为青藏高原应以刚性块体变形模式为主，应变主要被块体边界断裂所吸收。近期基于阶地演化与断裂位错分析，对前人的研究结果进行了重新分析表明，青藏高原主要大型活动断裂的滑动速率一般不超过10mm/a(Cowgill，2007;Zhang et al.，2007;张培震等，2008;Gold et al.，2009)，从而支持青藏高原应以连续变形模式为主，边界断裂只吸收了部分应变。由此可见，断层滑动速率对于区域构造格局的认识有本质影响。

近年来，随着各种测年技术的发展，例如:常规14C测年、加速质谱仪14C测年(AMS)、热释光、光释光以及宇宙成因核素等，测年精度有了极大提高，测年最小年限可以达到千年甚至百年。由于全新世地质体经历时间较短，保存较为完好，为野外测量与识别提供了方便，从而使得在活断层调查中利用全新世地质体获取滑动速率的应用越来越广泛。全新世地质体所经历时间较短，累积位错量与其对应年代的准确度会对滑动速率的计算有明显影响，较小的年龄误差就会造成较大的滑动速率偏差。走滑断裂滑动速率受侧向位移影响很大，在滑动速率计算中更应谨慎处理。在走滑断裂滑动速率的计算中，地质体实测年龄与实际累积位错时间不匹配会使速率计算结果产生不确定性，其来源主要有2个:1)累积位移时间是否与所测地质体年代相符合;2)地质体位移形成过程中所受到的侵蚀。本文从全新世年轻地质体(1ka甚至0.1ka)的角度出发，针对利用全新世地质体测定断层滑动速率的方法中的不确定性进行探讨，并对侧向位移的影响进行量化分析。

1 断层滑动速率获取的手段

断层滑动速率指的是断层两盘相对运动在某一时间段内的平均速度(丁国瑜，1982，1993;Wallace，1987;邓起东等，2002;张培震等，2008)，是断裂带上应变累积速率的表现之一，经常被作为断裂地震危险性评价的重要参考(Molnar，1979;闻学泽，1991，1993;Field，2007)。目前断层滑动速率主要是利用主要地貌面的总位移量与累积时间的比值来获得，地貌面的位移量一般由阶地位错量或者代表阶地位错的冲沟、阶地陡坎的位错来获得(随着野外测量技术的发展，标志物距离的测量误差可以忽略，主要问题来源在于不同人对位错标志物的认定存在较大差异，由位错量测量误差以及标志物认定差异而导致的滑动速率偏差不在本文讨论范围之内);位错累积时间一般由地质体实测年龄获得。阶地演化分析表明，利用对应阶地的位错及其上下限年代即可获得对应的滑动速率(Cowgill，2007;Zhang et al.，2007;张培震等，2008;Gold et al.，2009)。上述方法需要确定断层位错的起始时间，在接近万年甚至更长时间尺度上所得结果会较为准确，但是对千年甚至百年尺度的地质体来说，随着时间尺度的减小，所获取的滑动速率受侧向位移的影响会逐渐增大。因此，利用全新世地质体获取断层滑动速率的方法需要仔细分析侧向位移所带来的不确定性。

假设断裂真实滑动速率不变，那么可以根据以下公式计算滑动速率:

式(1)中:Rc为断层滑动速率，D为位错量，T为地质体发生位错的年龄。从式(1)可见，所计算的滑动速率与样品采集时地质体的年龄相关，如果地质体年龄与位错量不匹配，则会造成滑动速率偏离实际情况。通常情况下，地质体的年龄与其位错间的匹配性并没有得到应有的重视。

2 断层滑动速率不确定性分析

利用河流阶地位错来获得滑动速率是活动构造研究中非常普遍的情况，对于走滑型断裂来说尤其重要。如图1所示，T0/T1阶地陡坎在持续接受河流侵蚀、冲刷，因此，其位错较难保存。但是，当最后一次地震事件距今很近的情况下，河流还未将T0/T1阶地陡坎侵蚀掉，或者强震复发周期很短，每次地震事件以后，河流均难以将同震位错量完全侵蚀掉，从而在T0/T1阶地陡坎上保留下位错证据(Cowgill，2007)。如果野外考察不仔细进行分析，那么，利用这一最新阶地陡坎位错与年龄来计算滑动速率，将会得到错误结果。因此，只有尽量选取阶地陡坎位错形成后未遭受河流侵蚀作用的累积位错量及其对应年龄，才能获得较为准确的滑动速率结果。

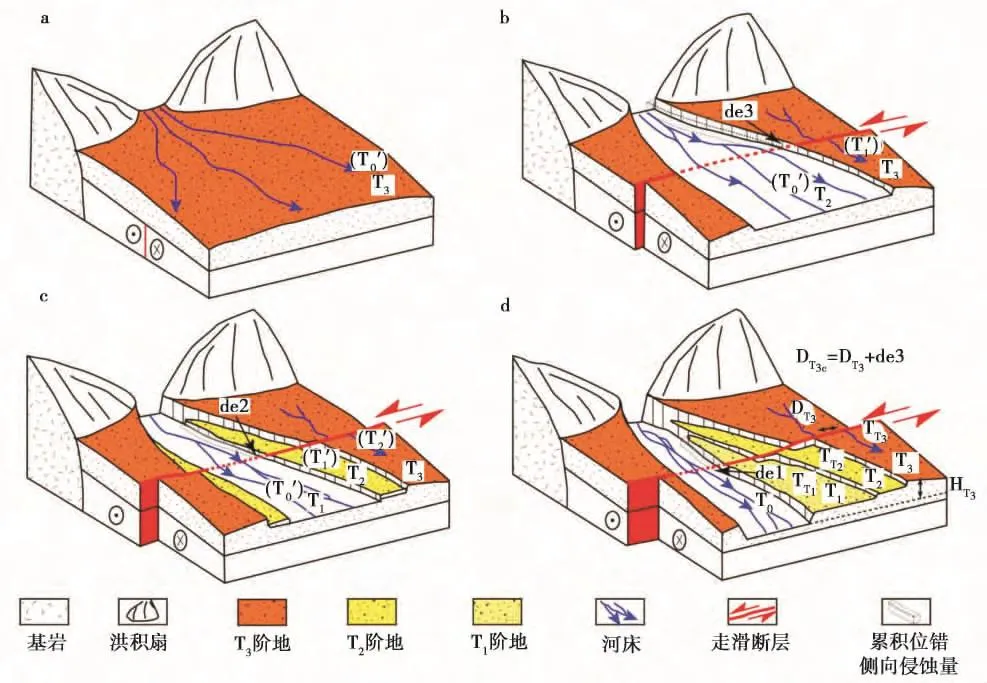
图1 走滑断裂带河流阶地与位错演化示意图Fig.1 Block diagrams showing plausible sequence of terrace offsets by strike-slip faulting.

在阶地发育较好的地点，由于老阶地陡坎均在其Ⅰ级阶地(T1')时期接受河流冲刷，实际累积位错量会被侵蚀、冲刷掉一部分，但是在阶地成为Ⅱ级(T2')及其以上的高级阶地以后，由于其与河床之间分布了Ⅰ级阶地，高阶地陡坎不再接受到河流侵蚀冲刷，保存的位错量更能代表强震累积位错量(图1)。因此利用高级阶地面自从Ⅱ级阶地形成(比其年轻的Ⅰ级阶地已经离水)以后再累积的位错量与对应时间计算可得实际滑动速率值，即利用高－低阶地累积位错量之差与其对应阶地年龄差(差值法)来计算滑动速率，在每级阶地拔河高度近似呈等差分布，且侧向位移较恒定的理想状况下，可以从一定程度上减少上述2种因素对滑动速率的影响。在各级阶地拔河高度不呈等差分布情况下，可以利用各级阶地年龄及其相应拔河高度对T2以后位移累积时间进行推算，本文对此情况进行简单的理论分析。根据阶地演化模式分析可知，侧向侵蚀主要发生在T1阶地时期，在T2阶地形成后，即不再接受侧向侵蚀，则可以根据T1和T2阶地拔河高度、年龄推算T2阶地不接受侧向侵蚀的年龄。

假设滑动速率为R，侧向侵蚀速率为E，T1阶地年龄为TT1，拔河高度为HT1(图2)，野外测量累积位移量为DT1，实际累积位移量为DT1c;T2阶地年龄为TT2，拔河高度为HT2，野外测量累积位移量为DT2，实际累积位移量为DT2c;以此类推，Tn阶地年龄为TTn，拔河高度为HTn，野外测量累积位移量为DTn，实际累积位移量为DTnc;则Tn阶地上接收侧向侵蚀年龄为

实际累积位移量为

滑动速率计算公式即为

在式(4)中，要解2个未知数E与R，需要已知3组阶地位错量、年龄和拔河高度等数据。如果所计算的侧向侵蚀速率E大于平均滑动速率R，则说明在T1阶地上较难累积位错;如果野外实际测量T1阶地上保留了部分位错，则说明为最近地震事件同震位错，或者实际情况与本文介绍的阶地形成模式不符，不能利用式(2)～(4)计算滑动速率及侧向侵蚀速率。如阿尔金断裂阿克塞野外点，其T1阶地拔河高度为3m，阶地年龄为2.2ka，T2阶地拔河高度为5m，阶地年龄为6.5ka，而T2'阶地拔河高度为8m，阶地年龄为9ka，但是阶地陡坎T2/T1位错量达145m，阶地陡坎T2'/T2位错量为 165m(图 2)(Mériaux et al.，2005)。由此可见，其阶地年龄、拔河高度及位错量数据之间不匹配，此类位错点不适用上述计算方法。此时可通过差值法，即高级阶地与低级阶地对应位错与年龄差值相除，即用式(5)来计算滑动速率(Ren et al.，2013):

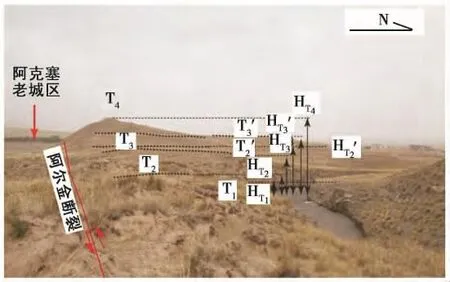
图2 阿克塞老城以东多级河流阶地被阿尔金断裂断错图Fig.2 Terrace levels displaced by the Altyn Tagh Fault，east to the old Aksay city.

Cowgill(2007)提出，计算走滑断层滑动速率应该利用高低阶地位错差值与高Ⅰ级阶地的废弃年龄来计算。沿阿尔金断裂车臣河，他利用此方法计算得到的滑动速率为 (9.4±2.3)mm/a。这一方法大大改进了前人利用对应阶地年龄与位错所得到的超大滑动速率值(Mériaux et al.，2004，2005)。但是，往往阶地位错累积时间并不一定对应其废弃年龄，而可能代表自T1'以来的年龄，因此其中T1'所经历时间也被错误地包含在滑动速率计算中。累积位错的侧向侵蚀以及单次地震事件的影响均未剔除。为了剔除这些因素的影响，这里介绍了一种差值法。这一计算方法中，侧向侵蚀的影响能够被全部或者部分剔除，从而降低这些因素对滑动速率的影响(表1)(Ren et al.，2013)。但是，由于一些地点拔河高度和T1阶地年代等信息未知，因此，仅仅在昆仑断裂带上，利用式(2)～(4)进行了滑动速率计算，其他点则采取了最简单的高低阶地年龄与位错差值法计算滑动速率。

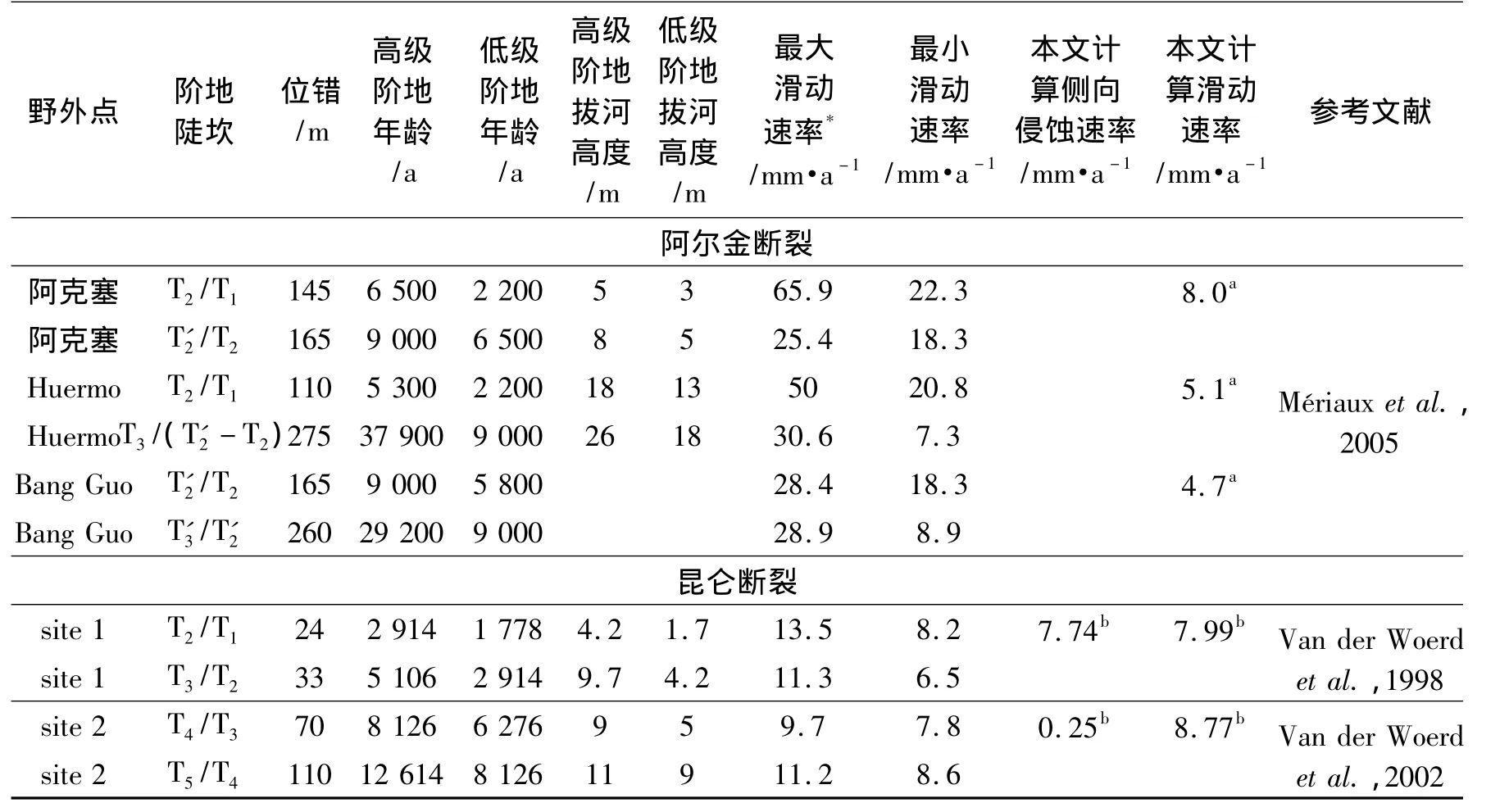
表1 差值法计算所得滑动速率与传统方法所得最大和最小滑动速率Table 1 Comparison of maximum and minimum fault slip rate calculated by differential method with that from other methods

在阿克塞旧城区以东发育多级阶地(图2)，Mériaux等(2005)曾经在此处开展工作，对多级阶地位错与年代进行测量，最终利用多级阶地位错计算了滑动速率，结果为18.3～22.3mm/a(表1)。但是野外实地考察发现，该处阶地只在冲沟一侧保存，在另外一侧并未保存，即所得阶地位错量并非真实阶地位错量，而是阶地陡坎后缘与现今冲沟壁之间的相对距离。并且从Ⅰ级阶地T1所在位置分析可知，该阶地可能并非形成阶地后被断错，而很可能是冲沟断错之后形成。因此，利用Ⅰ级阶地年龄与冲沟位错来计算滑动速率所得结果会偏大。利用本文提出的差值法重新计算得到，阿尔金断裂在阿克塞旧城区滑动速率为8.0 mm/a(表1)，其他点速率为4.7～5.1mm/a，低于Mériaux等(2005)的计算结果。而本文计算结果与前人获得的低地质滑动速率相一致(新疆维吾尔自治区地震局，1992)，也为前人通过现今GPS观测提出的低缩短速率和滑动速率(Bendick et al.，2000;Shen et al.，2001;Wallace et al.，2004;Zhang et al.，2004)提供了长地质时期上的低滑动速率证据;这一速率也与古地震研究得到的1ka复发周期结果相一致(Washburn et al.，2001，2003)。沿昆仑断裂，重新计算得到的滑动速率为7.99～8.77mm/a，也与前人的结果一致(Table 1)(Zhang et al.，2004;Shen et al.，2005;Lin et al.，2008)。昆仑断裂上古地震研究得到的复发周期为1ka左右(Guo et al.，2006，2007;Kirby et al.，2007;Lin et al.，2008)，与本文新计算结果一致。

3 结论

利用年轻地质体获取断层活动速率是全新世活动断裂研究的重要手段。但是，由于测年结果表现的是到现在为止地质体所经历的时间，而地质体实测年龄又包含了地质体接受侧向侵蚀的时间，所以并不能准确代表位错累积时间。利用地质体实测年龄计算滑动速率值获得的是长期平均值，地质体累积位错所经历时间的准确与否是滑动速率准确与否的关键。

走滑断裂上河流阶地演化与断层位错分析表明，在考虑侧向侵蚀的情况下，利用本文提出的算法可以通过多级阶地的位错量、年龄及拔河高度等数据同时计算断层滑动速率与侧向侵蚀速率，这可以在一定程度上减少侧向侵蚀因素对走滑断裂滑动速率的影响，提高所获滑动速率的可靠程度。在所计算的侧向侵蚀速率远大于滑动速率的情况下，在Ⅰ级阶地上不累积位错。如果野外实际调查发现在Ⅰ级阶地上保留了位错，则说明该处实际位错累积模式与本文提出的模式不符，不适合式(2)～(4)中的算法。这时可以利用高－低阶地累积位错量之差与对应阶地年龄差(差值法)来来计算断层滑动速率，也可以在一定程度上提高所计算滑动速率的准确度。