基于基坑降水优化设计的地面沉降数值模拟
2014-12-14李贵仁
赵 珍,李贵仁
(华北有色工程勘察院有限公司,河北 石家庄 050021)
深基坑降水工程的设计,不仅包括基坑降水区域应达到指定降深,而且还包括基坑降水对周边地面沉降影响的最低。现阶段,降水所引起的坑周围地面沉降量一般是采用太沙基一维固结理论进行计算预测,但对于边界不规则、岩层各向非均质异性、含水层间存在垂向补给或排泄的复杂地下三维流场,用解析解法估计降水井抽水量及坑周的沉降量明显存在较大的误差。
近年来,数值模拟方法发展迅速,已逐渐被应用到基坑降水工程中,在预测复杂三维流场下坑周边流场的水头及地面沉降量在时间与空间上分布上取得了较好的效果,对基坑降水施工有重要的实践意义。
1 研究区概况
天津地铁XX站基坑为长方形,中心里程为CK4+116.824,全长 200 m,总宽 20.7 m,基坑施工区自然地面标高约为3.15 m,基坑开挖较深,标准段基坑挖深16.62 m(标高为-13.47 m),最大开挖深度 18.5 m(标高为 -15.35 m)。
车站场地范围内地层分为5个大层:第四系全新统人工填土层;第I陆相层;第 I海相层;第 II陆相层上部为湖沿相沉积土,下部为河床—河漫滩相沉积层;第III陆相层。
地下水可分为两种类型:孔隙潜水与微承压水。孔隙潜水存在于①层人工杂填土及第③、第④层粉质粘土中。微承压含水层主要分布在⑥ -2、⑦ -2、⑦ -6的粉土层中,以⑤-1粉质粘土、⑥-1粉质粘土为相对隔水顶板。微承压含水层厚度较大,分布相对稳定,水位受季节影响不大,变化幅度小。
2 地下水流数值模拟模型
2.1 概念模型
本文借用降水影响半径来帮助确定渗流计算的范围,取以基坑为中心,800 m×800 m区域为最终模拟范围。
模拟深度取40 m,完整的包含了本场地上部潜水和下部微承压含水层,第一层为大气降水入渗补给的自由面边界;底边界为隔水边界。模型的四周(正方形边缘)为第一类边界(定水头边界);
根据场地的水文地质条件,将计算区垂直方向上自上而下剖分成7层(见表1)。
深基坑降水过程中,伴随土体孔隙中水的大量排出,孔隙水应力的消散,土体的有效应力增加,导致土体固结,底层被压缩,宏观上反应为地面沉降或变形,这实际上就是渗流场改变引起应力场改变,应力场改变引起位移场发生相应改变的过程,正是各层水位的变化才导致可压缩地层的压缩[1],因此,地层压缩层的划分与上述水文地质概念模型一致。

表1 模型分层情况表
2.2 数学模型
基于上述概念模型,可建立场地由降水引起地面沉降的数学模型,该模型由两个模型构成。地下水渗流方程数学模型:

式中:Kxx为水平渗透系数,且等于y轴渗透系数;Kzz为垂向渗透系数;Ss为贮水率;Γ1为第一类边界条件。
变形模型[2]:基坑周边地面沉降就是基坑降排水引起的弹性和非弹性释水引起的相应的应变的总和:
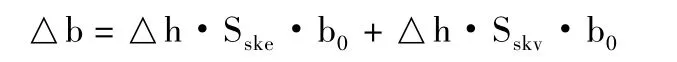
式中:△b为含水层压缩变形量(m);△h为水头变化值(m);b0为可压缩含水层的厚度(m);Sske为骨架成分的弹性储水率(1/m);Sskv为骨架成分的非弹性储水率(1/m)。
将以上两式通过水头项耦合起来形成了耦合模型。
图1 研究区网格平面剖分图
2.3 数值模型
采用地下水三维流运动模拟软件包Processing Modflow中的Modflow和Interbed-Storage数值模拟模块求解。
采用矩形有限差分的离散方法对模拟区进行剖分,将计算域在垂向上分为7层,平面共剖分单元80×80个,每层单元格为6 400个,7层共剖分44 800个单元。
将模拟时间进行离散,共将模拟期共划分为3个应力期,共72个时段。
2.3.1 参数的选取
考虑到基坑所在场区面积小,仅0.64 km2,即同一岩层在场区水平向水文地质参数变化不大,无明显分区,因此,对模型主要在垂向上按层进行参数分区,即模型每个层均为一个分区。各分区的参数初始值依据场区地质勘察报告建议值给定,然后采用试错法确定,模型水文地质参数分区见表2。

表2 模型水文地质参数分区表
2.3.2 初始条件
初始水位h(m):由于模拟区地势较平坦,且模拟范围较小,因此结合当地水位资料,确定模拟范围内水位水平,潜水含水层初始水位为1.8m,微承压含水层初始水位标高为0.17 m。
初始压缩量[3](m):由于本次模拟是要计算基坑降水所引起的最终压缩量和沉降量,最终结果不考虑初始压缩量和出事沉降量,因此将其设置为0。
前期固结水头(m):根据研究区水位动态资料,本模型中初始前期固结水头为地面标高3.15 m。
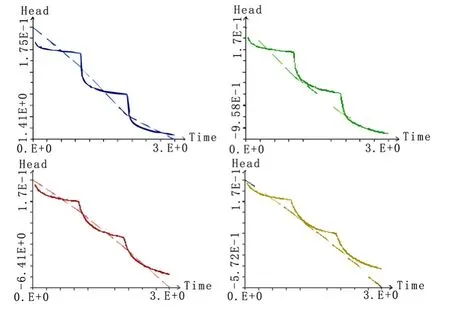
图2 各观测孔水位拟合曲线
2.3.3 模型识别
选取基坑场区的抽水试验期作为模型的识别阶段,利用6个承压观测井水位资料及14个地面沉降监测点监测数据对模型进行拟合,让模型运行72个时段,记录下每个时段各观测孔所在结点水位及沉降量,若各种计算初值给的合理,计算的(H-t)曲线和(S-t)曲线应与实测的(H-t)曲线和(S-t)曲线基本拟合,否则要反复各水文地质参数,并进行试算,一直到曲线拟合程度满足要求为止。
由图2可知,模型的地下水位计算值与观测值拟合效果较好,说明模型的地下水位计算值与观测值基本一致。

图3 部分监测点沉降量拟合曲线
由拟合情况可知,大部分监测点拟合效果较好,可以认为本次建立的地面沉降模型基本符合实际情况,可以用来进行地面沉降预测。
2.4 预测结果及分析
按照拟建工程的施工要求,拟建基坑坑内采用管井降水,以降低浅部水位至基坑坑底 0.5~1 m[4],但为了防止微承压含水层发生突涌现象,需降低该含水层的水头,因此在模拟中将基坑内地下水位降至 -15.65 m以下时,基坑工程可安全施工。
综合考虑基坑所处场区的水文地质条件及施工要求,坑内共设26口降水井,单井抽水量为42 m3/d。为了更好的展示沉降模拟结果,在模型中设置23个沉降观测点。
根据模型识别以及基坑降水设计,参照施工要求,该工程基坑在降水后水位应降至 -15.65 m。经运行模型,在降水9 d后可达到预期目的。
由模拟结果可知,第9天时,基坑内部最大沉降量达0.197 m,基坑外围最大沉降量为0.001 53 m,沉降范围以基坑为中心的240 m范围内,场区地面沉降的空间分布呈基坑内沉降最大,由坑往外,地面沉降值逐渐减小的规律。
根据以上预测结果认为,该场区基坑降水会导致附近地面的沉降,对场区邻近一线周边环境等可能产生一定的不利影响。
3 基坑降水的优化设计
根据施工要求,本次基坑降水需满足在降水15 d内坑内地下水水位降至标高 -15.65 m以下,同时要满足单井抽水量不高于72 m3/d的限制,本着在规定时间内用最少的抽水量完成降水要求,并对基坑周围造成的环境影响最小的原则,对本次基坑降水进行优化设计。
用模拟软件分别在基坑内设置16口、20口、24口降水井,并将各个降水井设置不同的抽水量,利用模型输出基坑内水位降至目标深度时所需的时间、总抽水量及连续墙外10 m内平均地面沉降量,各方案模拟结果见表3。

表3 各方案降水效果对比
通过表3可以看出,方案9在规定时间内达到目的降深的同时,所需抽水量最少,对周围环境的影响最小,因此本次基坑降水的最佳方案为坑内设置24口井,单井抽水量为60 m3/d。
4 结语
(1)以天津地铁XX站深基坑降水工程为例,在渗流计算区域确定、模型垂向分层、各层顶底标高、初始条件分布、地下连续墙和降水井设置等问题处理的基础上,运用Processing Modflow建立了基坑降水及地面沉降计算的数值模型,并根据场区水位观测及地面沉降监测资料,识别了模型各层(分区)的水文地质参数,并运用模型模拟预测了基坑降水特点及地面沉降的时空分布规律。
(2)根据本例中模型,对降水井进行了优化,得出基坑降水的最优设计方案为24口井,单井抽水量60 m3/d,在符合同样的基坑降水施工要求的情况下,大大降低了基坑降水的成本。
[1]杨少华.城市建设引起地面沉降的数值模拟研究[D].北京:中国地质大学.2009.
[2]付延玲,郭正法.Processing Modflow在地下水渗流与地面沉降研究中的应用[J].勘察科学技术.2006,18(4):19-23.
[3]郑刚.天津市地下工程中地下水的影响及控制[J].施工技术.2010,39(9):1-5.-33.
[4]徐耀德,童利红.利用Modflow预测某基坑降水引起的地面沉降[J].水文地质工程地质.2004.21(6):96-100.
[5]骆祖江,刘金宝.深基坑降水与地面沉降变形三维全耦合模型及其数值模拟[J].水动力学研究与进展.2006.21(4):479-483.
