应用支持向量机评价土壤环境质量

姜 雪,卢文喜*,杨青春,赵海卿 (.吉林大学环境与资源学院,地下水资源与环境教育部重点实验室,吉林长春 300；.沈阳地质矿产研究所,辽宁 沈阳 003)

应用支持向量机评价土壤环境质量

姜 雪1,卢文喜1*,杨青春1,赵海卿2(1.吉林大学环境与资源学院,地下水资源与环境教育部重点实验室,吉林长春 130021；2.沈阳地质矿产研究所,辽宁 沈阳 110032)

基于野外采样和室内分析相结合的方法,采用电感耦合等离子体质谱法(ICP-MS)对羊草沟煤矿研究区表层土壤样品中的 Cd、Cr、Zn、Pb和Cu含量进行测定,应用非线性支持向量机模型中的分类支持向量机,选用sigmoid核函数,利用MATLAB编写程序,进行土壤环境质量评价,并利用模糊综合评判法对评价结果进行验证.在此基础上,运用对应分析方法对样品和变量进行了关联分析,进一步了解重金属污染特征.评价结果表明,研究区土壤环境质量多为Ⅰ类,与模糊综合评判法的相同率达到 91.67%,将支持向量机用于土壤环境质量评价是可行的.相比于传统的评价方法,支持向量机采用结构风险最小化原则,将复杂的非线性问题转化为线性问题,成功的解决了多分类、高维运算等问题.

支持向量机；土壤环境质量评价；重金属；羊草沟煤矿

目前常用的土壤环境质量评价方法按性质可分为3大类:定性、定量和定性与定量相结合.其中定性方法包括定性模糊集、聚类分析法等;定量方法包括指数法、回归分析法、概率法等;定性与定量相结合的方法包括模糊综合评判法、层次分析法、相关分析法、多元统计法等[1-2].然而,在土壤环境质量评价过程中,评价因子与环境质量等级之间存在着复杂的非线性映射关系,上述方法并未很好地处理这种非线性映射关系,且在评价过程中需要人为给定各评价因子权重,从而使评价结果缺乏可靠性、客观性和通用性[3].支持向量机(Support Vector Machine,SVM)模型通过用内积函数所定义的非线性变换将输入空间变换到一个高维空间,在高维空间中寻找输出变量和输入变量之间的非线性关系[4],具备非线性模式识别的能力.目前 SVM 已广泛应用于人脸图像识别、手写字识别、信号处理、语音识别、水质评价、文本分类、遥感图像分析等领域[5-8].而将该法应用于土壤评价领域目前尚很少见.本文采用支持向量机方法来评价土壤环境质量,以羊草沟煤矿研究区为例,探讨 SVM 建模过程和评价效果,旨在对 SVM 模型技术在土壤环境质量评价领域提供借鉴意义,同时讨论羊草沟煤矿土壤环境现状.

1 SVM基本理论

支持向量机(SVM)是基于统计学习理论发展而来,它针对有限样本情况下模式识别中的一些根本性问题进行系统的理论研究.相比于传统机器学习方法,支持向量机采用结构风险最小化准则,在最小化样本点误差的同时缩小模型泛化误差的上界,从而提高了模型的泛化能力,在很大程度上解决了模型中的过学习、非线性、维数灾难等问题[9].

SVM通过构建最优分类超平面将各类样本正确无误地分开,同时使分类间隔最大,距最优分类超平面最近的向量为“支持向量”(SV)[10].支持向量机可分为线性支持向量机和非线性支持向量机,在土壤环境质量评价过程中,评价因子与环境质量等级之间存在着复杂的非线性映射关系,因此本文主要介绍非线性支持向量机问题.

非线性问题可以通过非线性变换转化为某个高维空间中的线性问题,在变换空间中寻求最优分类超平面[11].这种变换可以通过核函数来实现.因为核函数 K ( xi,xj)对应某一变换空间的内积即 K (xi,xj)=ψ( xi)·ψ ( xj). K ( xi,xj)提供了避免“维数灾难”问题的办法.其基本思想如下:SVM 利用某种事先选择的非线性映射φ,将输入向量x映射到某个高维特征空间,然后在高维空间中求最优分类超平面[12-14].

设样本集为(xi, yi),i = 1,2,…,n ;y= { 1,-1 }是类别标号,超平面方程为:

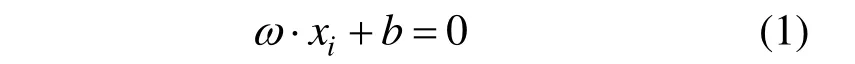
在约束条件上加入一个松弛变量 ξi≥0,这时的最大间隔超平面称为广义最优分类超平面[15-17].则约束条件变为:

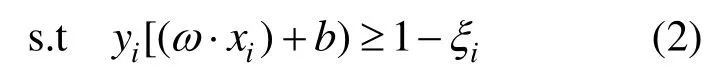
对应的优化问题转变为:

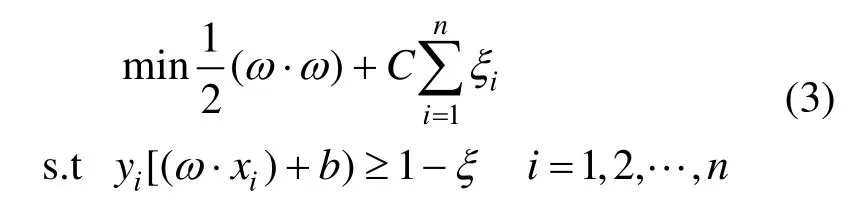
式中:ω为权向量,b为偏置,iξ为松弛变量.C>0是控制惩罚程度的常数(惩罚因子),C越大,惩罚就越大.引入Lagrange乘子βα,有:

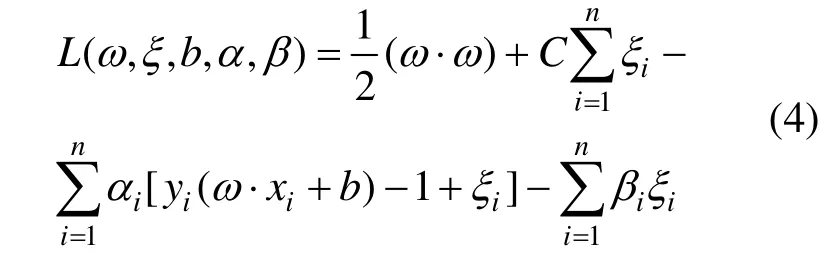
Lagrange函数L在鞍点处是关于ω,ξ,b的极小点,对ω,ξ,b分别求偏导,再整理L最终可以得到原问题的对偶问题:

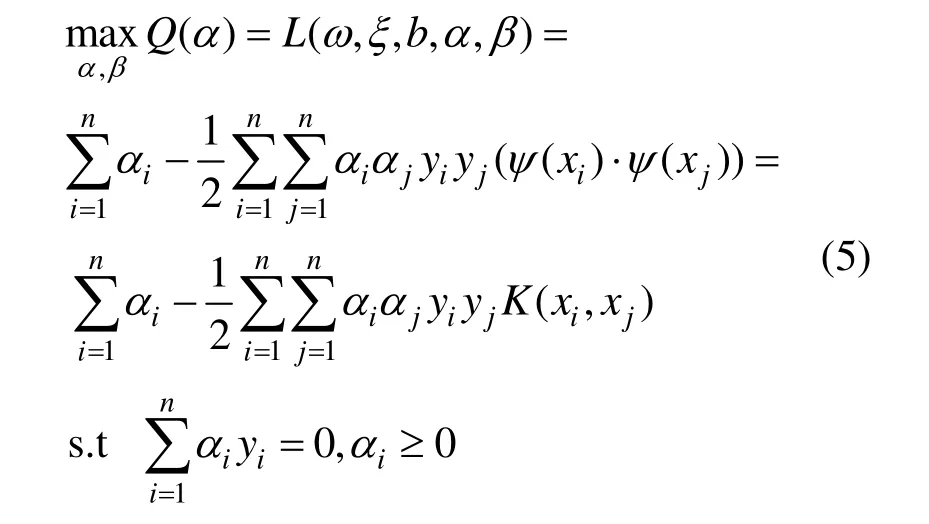
则最优判断函数为:

常用的核函数有:线性核函数、多项式核函数、径向基函数核函数和二层神经网络核函数.

2 应用实例

2.1 研究区概况

长春市羊草沟煤矿位于长春市东部,西距长春市18km,东距九台市30km.属吉林省九台市东湖镇所辖.地理坐标东经: 125°33′26.1″～ 125°36′17.2″,北纬:43°57′27.9″～43°58′51.9″,矿区面积 16km2.研究区土地类型主要为耕地,矿区气候属温带大陆性季风气候,年平均降雨量为 597.7mm.腰站河为研究区内一条季节性河流,发源于矿区南部,向北流向矿区东部,矿区内流域面积 2.5km2.五一水库是区内最大的地表水体,位于矿区西部,该水库最小库容265万m3,最大库容2443万m3.

2.2 数据来源

采用网格化均匀布点,将整个羊草沟煤矿研究区划分成 1km×1km 的采样单元格,采样密度为1组/km2,采样深度15cm,共采集24组样品,土样采集点分布见图1.根据《土壤环境监测技术规范》[18]要求,将运回的土壤样品风干,过200目筛成制备样.

测试方法:取过200目筛的样品0.1000g于酸煮洗净的 PTFE密罐中,依次加 3mL硝酸(68%,GR),1mL氢氟酸(40%, GR),1mL过氧化氢(30%,GR)混匀后加盖密闭,在 180℃烘箱中加热 48h.冷却后于自动控温电热板上 100℃蒸至近干,赶走HF,加2mL 5% HNO3再加盖密闭,于140℃烘箱中加热3h,冷却后,样品转移到干净的50mL容量瓶中,稀释定容,摇匀,用电感耦合等离子体质谱仪(ICP-MS, Aglient7500a, USA)进行重金属元素测定[19].测定指标为 Cd、Cr、Zn、Pb和 Cu.评价指标即选择实测的5种重金属元素.

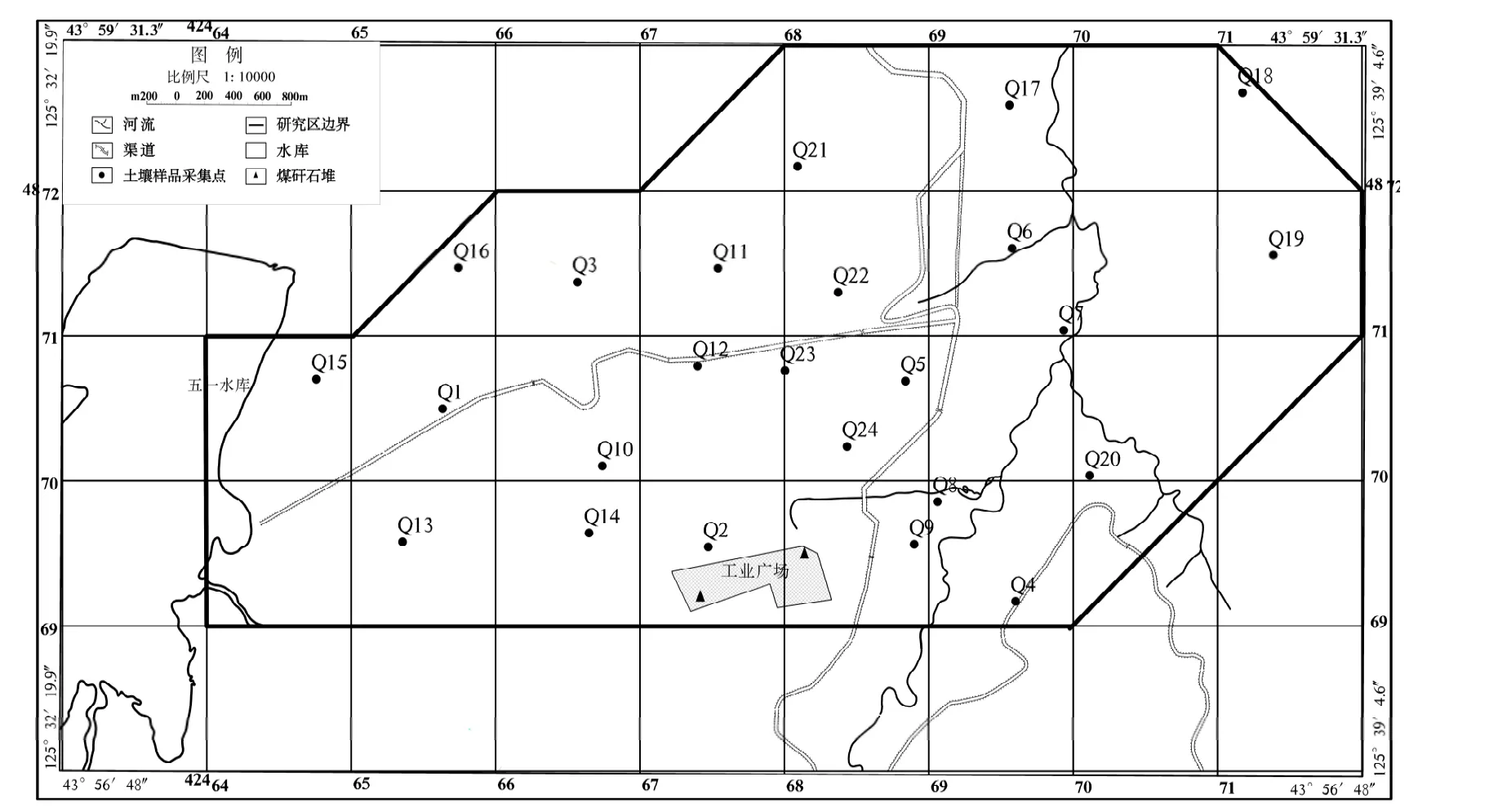
图1 土样采集点位置分布Fig.1 The location of soil sample points

从表 1中可以看出,研究区土壤环境质量与国家标准相比较好,但经过与研究区土壤背景值进行对比可知,研究区土壤中重金属Zn、Pb元素含量的平均值均超过了土壤背景值,表明这 2种重金属元素已经对该区的土壤造成了污染.煤矸石中各重金属含量均超过研究区土壤背景值,Cr、Cu、Zn、Cd和 Pb含量分别为土壤背景值的 1.25、1.27、2.00、1.20、1.13倍,其中 Zn含量超背景值最多.

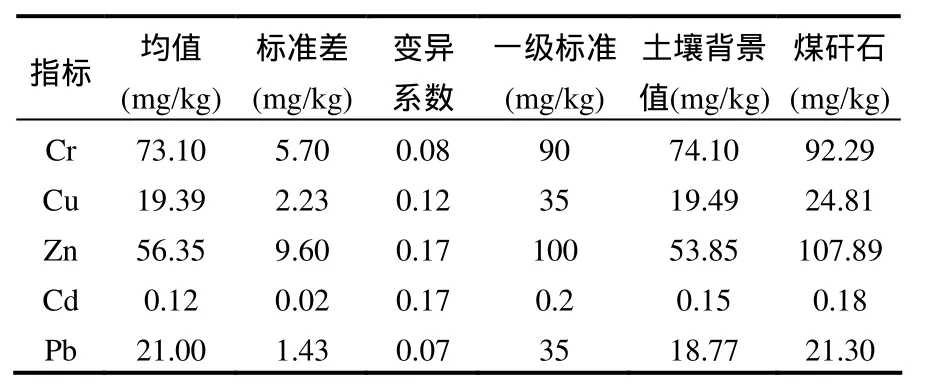
表1 重金属含量统计结果Table 1 The statistical results of heavy metal contents

土壤中各种金属含量的波动性不大.变异系数在0.07～0.17之间,变异强度弱-中等.

2.3 SVM模型的构建、应用和验证

根据土壤环境质量分级标准[20](GB15618-1995),利用MATLAB中的Rand函数生成随机样本,即在土壤环境质量的3个等级内,各个指标可以在标准中划分的取值范围内任意取值,若土壤各评价指标的取值均在某一等级范围内,则该土壤肯定符合该等级土壤环境质量标准[3].5种参评因子的分级标准如表2所示.

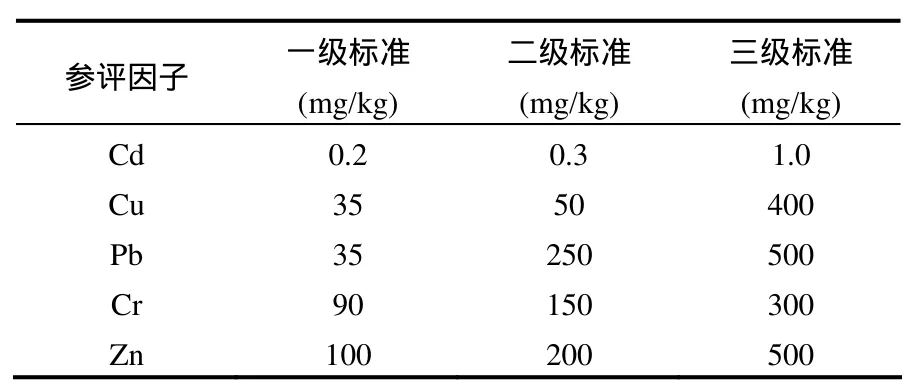
表2 五种参评因子的分级标准Table 2 The classification standard of five kinds of the evaluated factors

本文在小于土壤环境质量一级标准取值范围内生成 200对训练样本,一级、二级标准之间生成200对,二级、三级标准之间生成200对,共随机生成 600对训练样本.测试样本即为实测的24组数据.模型构建步骤如下:

(1)数据归一化、去噪.归一化采用公式(7),将数据归一化至[0,1]之间.

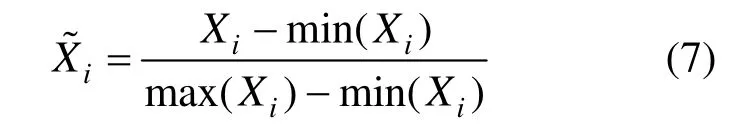
(2)确定 SVM 模型结构.5种重金属元素(Cd、Cr、Zn、Pb、Cu)的含量作为输入向量,土壤环境质量级别为输出.

(3)确定核函数.分别将线性核函数、多项式核函数、径向基函数核函数和二层神经网络核函数这四种不同的核函数带入模型进行对比试验.根据试验结果,本文选用二层神经网络核函数最为合适,该核函数的表达方式为 K ( xi, xj)=tanh(γ(xi· xj)+ r ),γ ＞0

(4)确定参数.由于土壤环境质量等级评价属于非线性分类,故采用 C-支持向量分类(C-SVC)模型,该模型需设定惩罚参数 C,在对训练样本进行训练时,log2c设定-10到10之间,然后执行交叉验证参数寻优程序,选取最优参数 best c,作为惩罚参数.内核参数log2g设定-10到10之间,然后执行程序,选取最优内核参数best g.经训练,最优惩罚参数best c=1024,最优内核参数best g=128.

(5)建立模型.利用MATLAB编写程序,将所得到的最优惩罚参数和最优内核参数带入模型,训练随机学习样本,建立土壤环境质量评价模型,将24组测试样本带入评价模型,得到土壤环境质量评价结果.

2.4 结果与讨论

2.4.1 SVM与传统方法评价结果对比分析 相比于其他传统方法,模糊综合评判法在模型中引入隶属度和各个评价因子的权重,能较准确刻画环境质量客观存在的状况[21-22],故采用 SVM 评价的同时,又引进了模糊综合评判法对研究区土壤环境质量进行评价,将 SVM 评价结果与模糊综合评判法结果相比较(表3).

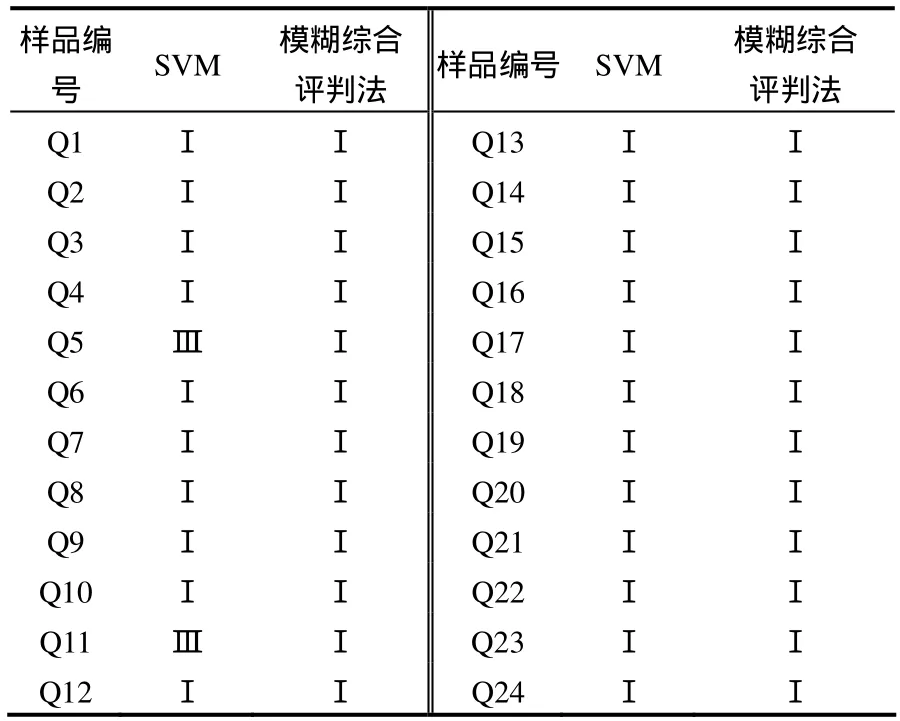
表3 SVM与模糊综合评判法结果对比Table 3 The comparison between SVM and fuzzy comprehensive evaluation

据表3分析可知,SVM与模糊综合评判法的评价结果相同率达到91.67%,研究区土壤环境质量多为Ⅰ类,评价结果表明,研究区土壤环境质量与国家标准相比较好,与调查访问结果一致,符合实际情况.

以该区土壤背景值为评价标准,运用单因子污染指数法、内梅罗综合污染指数法这两种传统方法进行了土壤环境质量评价.单因子污染指数法结果表明,各采样点Cr和Cd污染程度均为未-轻度污染;Cu、Zn、Pb的污染程度均属轻度.5种重金属元素污染程度由强至弱依次为:Pb>Zn>Cu>Cr>Cd.内梅罗综合污染指数评价结果显示,21%的土样点处于警戒线水平(土壤综合污染指数在0.7～1.0之间),而79%的土样点受到重金属的轻度污染(土壤综合污染指数在1.0～2.0之间).

单因子污染指数只能反映各污染物对环境的污染程度,不能给出土壤环境质量级别,而内梅罗综合污染指数法突出重金属含量最大的污染物对环境质量的影响,模糊综合评判法可以有效解决模糊边界问题,然而这几种方法并没有反映评价因子与环境质量等级之间复杂的非线性映射关系,而支持向量机模型通过用内积函数所定义的非线性变换将输入空间变换到一个高维空间,在高维空间中寻找输出变量和输入变量之间的非线性关系[4],具备非线性模式识别的能力,成功的解决了多分类、影响因素复杂、高维运算等问题.因此,本文运用支持向量机模型评价土壤环境质量可行,评价结果可靠.

2.4.2 相关性分析 具有相同(似)起源的重金属元素,其含量往往具有显著的相关性,因此研究土壤中各重金属含量间的相关性可以粗略地推断重金属的来源是否相同[23-24].本文运用 SPSS中的Pearson相关分析方法研究土壤中不同重金属元素间、土壤重金属含量与土壤pH值间的相关关系,相关性分析结果如表4所示.

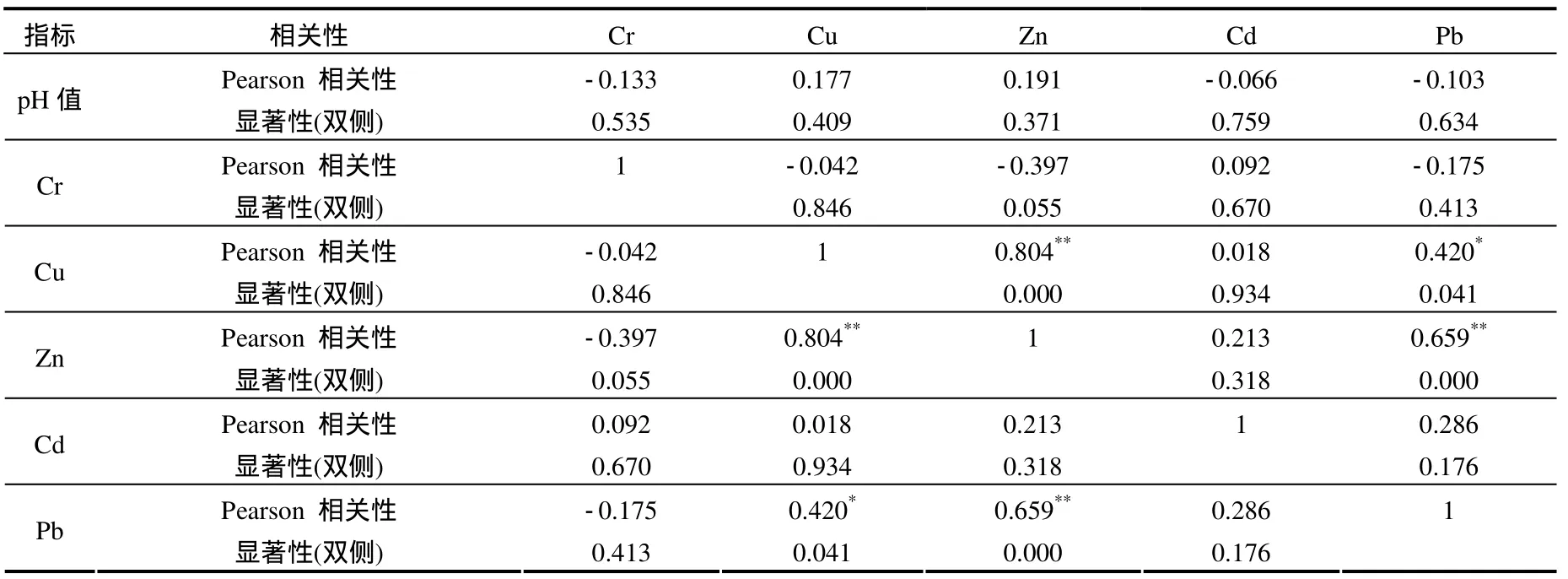
表4 土壤的各测试指标相关性分析结果Table 4 The correlation analysis results of the tested index

由表4可知,Cu与Zn、Zn与Pb在0.01水平(双侧)上显著相关,Cu与Pb在0.05水平(双侧)上显著相关,说明它们的来源极为相似,推测污染源为煤矸石.

2.4.3 运用对应分析方法对样品和变量进行关联分析 对应分析方法可以从因子载荷图上对样品进行分类,而且能够揭示每个分区的主要影响变量及依据;也可以对变量进行分类,提取出潜在的公因子,并揭示每个因子的含义[25-26].本文应用对应分析方法,对羊草沟煤矿研究区24个土样点的5个测试指标进行研究.

从图 2可见,24个样品点被分为 4个区.Ⅰ区:Q2、Q3、Q6;Ⅱ区:Q9、Q10、Q11、Q13、Q14、Q16、Q19、Q20、Q22、Q24;Ⅲ区:Q5、Q7、Q8、Q18、Q21;Ⅳ区:Q1、Q4、Q12、Q15、Q17.与Ⅰ区样品关系较为密切的重金属是Zn,该区附近有煤矸石堆积,而 Zn是煤矸石中重金属含量超背景值最多的元素,说明该区主要受到煤矸石堆的影响;与Ⅱ区样品关系较为密切的重金属是Pb和Cd;与Ⅲ区和Ⅳ区样品关系较为密切 的重金属分别是Cr和Cu.

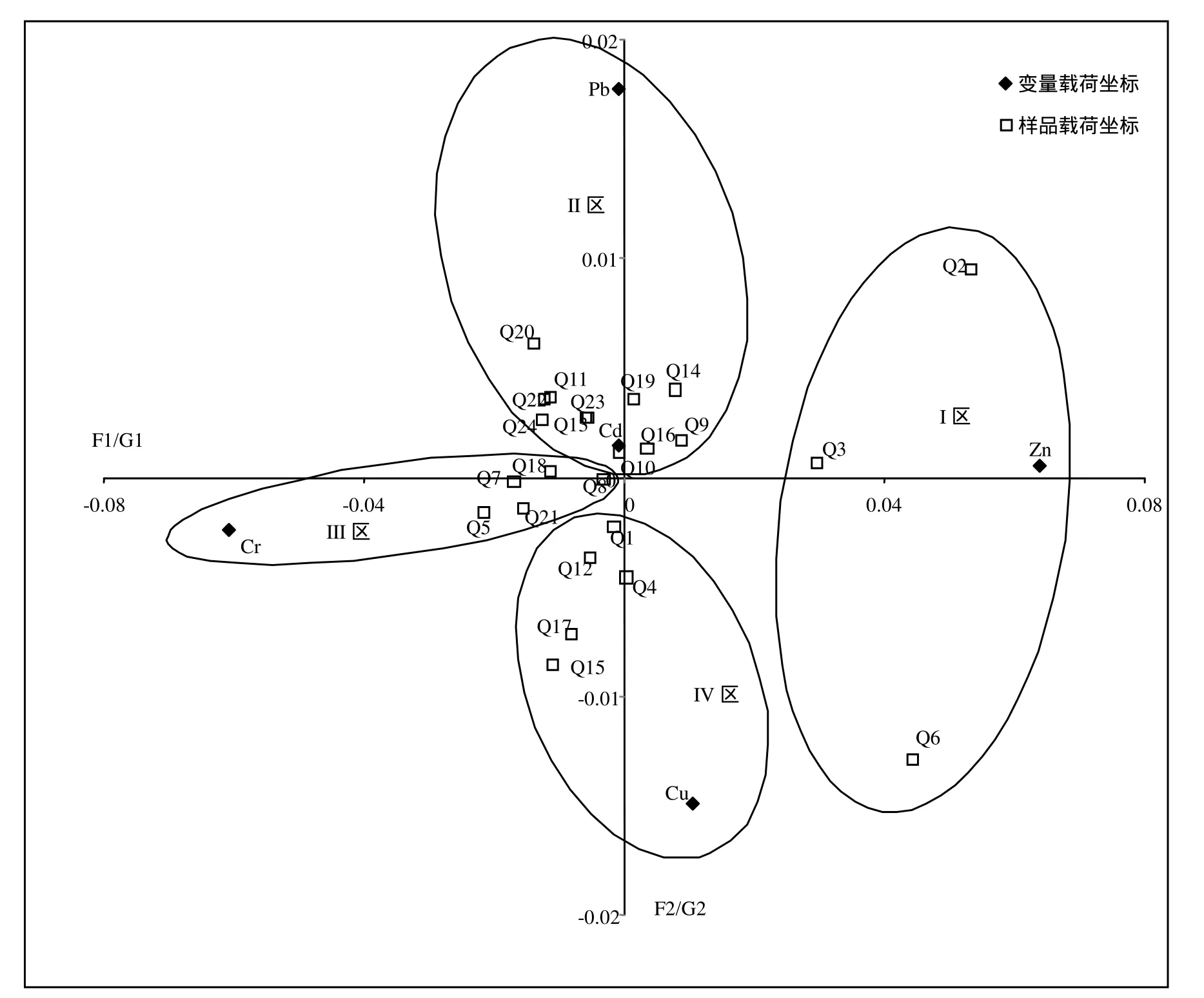
图2 对应分析因子载荷平面投影Fig.2 Loading plane projection map of correspondence analysis factor

3 结论

3.1 支持向量机模型评价方法与模糊综合评判法的结果相同率达到91.67%,并且评价结果与野外调查访问相符,说明将支持向量机应用于土壤环境质量评价是可行的.相较于模糊综合评价及其他传统的土壤环境质量评价方法,支持向量机采用结构风险最小化原则,将复杂的非线性问题转化为线性问题,成功的解决了多分类、高维运算等问题.

3.2 SVM 评价结果表明,研究区土壤环境质量多为Ⅰ类,说明研究区土壤环境质量与国家标准相比较好.单因子污染指数评价结果表明,由于该区土壤背景值较低,大部分土样中重金属含量超过了土壤背景值,说明该区土壤已经受到了部分重金属的污染.

3.3 Pearson相关分析结果表明,Cu与 Zn、Zn与Pb在0.01水平上显著相关,Cu与Pb在0.05水平上显著相关,说明它们的来源极为相似,推测污染源为煤矸石.

3.4 对应分析结果表明,研究区土壤样品可分为 4个区.与Ⅰ区样品关系较为密切的重金属是Zn,该区主要受到煤矸石堆的影响;与Ⅱ区样品关系较为密切的重金属是Pb和Cd;与Ⅲ区和Ⅳ区样品关系较为密切的重金属分别是Cr和Cu.

[1]蒋丽婷.河北省唐山市丰润区土壤中重金属分布及土壤质量评价 [D]. 北京:中国地质人学, 2006.

[2]余 涛.湖南洞庭湖地区土地质量地球化学评估 [D]. 北京:中国地质大学, 2006.

[3]杨忠平,卢文喜,龙玉桥.改进BP算法在城市土壤环境质量评价模型的应用 [J]. 重庆大学学报(自然科学版), 2010,32(2):99-103.

[4]于国强,张茂省,王根龙,等.支持向量机和BP神经网络在泥石流平均流速预测模型中的比较与应用 [J]. 水利学报, 2012,S2:105-110.

[5]梁宏霞.支持向量机模型研究及应用 [D]. 沈阳:辽宁师范大学,2009.

[6]Yoon H, Jun S C, Hyun Y, et al. A comparative study of artificial neural networks and support vector machines for predicting groundwater levels in a coastal aquifer [J]. Journal of Hydrology,2011,396(1):128-138.

[7]周建国,张希刚.基于粗糙集与灰色SVM的中国CO2排放量预测 [J]. 中国环境科学, 2013,33(12):2157-2163.

[8]李祚泳,张正健.基于回归支持向量机的指标规范值的水质评价模型 [J]. 中国环境科学, 2013,33(8):1502-1508.

[9]梁雪春,龚艳冰,肖 迪.一种多核加权支持向量机的水质预测方法 [J]. 东南大学学报:自然科学版, 2011,41(B9):14-17.

[10]Vapnik V N. The nature of statistical learning theory [M]. Berlin:Springer-Verlag, 1995.

[11]陈其松.智能优化支持向量机预测算法及应用研究 [D]. 贵阳:贵州大学, 2009.

[12]Sun A, Lim E P, Liu Y. On strategies for imbalanced text classification using SVM: A comparative study [J]. Decision Support Systems, 2009,48(1):191-201.

[13]武国正.支持向量机在湖泊富营养化评价及水质预测中的应用研究 [D]. 呼和浩特:内蒙古农业大学, 2008.

[14]Wu K P, Wang S D. Choosing the kernel parameters for support vector machines by the inter-cluster distance in the feature space[J]. Pattern Recognition, 2009,42(5):710-717.

[15]Leng B, Qin Z, Li L. Support Vector Machine active learning for 3D model retrieval [J]. Journal of Zhejiang University Science A,2007,8(12):1953-1961.

[16]Harris T. Quantitative credit risk assessment using support vector machines: Broad versus Narrow default definitions [J]. Expert Systems with Applications, 2013,40(11):4404-4413.

[17]Baly R, Hajj H. Wafer Classification Using Support Vector Machines [J]. Semiconductor Manufacturing, IEEE Transactions on, 2012,25(3):373-383.

[18]HJ/T 166-2004 土壤环境监测技术规范 [S].

[19]刘红艳,周 燕,王铁夫,等.ICP-MS法测土壤样品中铜铅的不确定度评定 [J]. 光谱学与光谱分析, 2011,31(4):1115-1118.

[20]GB/T 15618-1995 土壤环境质量标准 [S].

[21]Li W X, Zhang X X, Wu B, et al. A comparative analysis of environmental quality assessment methods for heavy metal-contaminated soils [J]. Pedosphere, 2008,18(3):344-352.

[22]梁 伟,张慧颖,朱孔来.基于模糊数学和灰色理论的城市生态环境竞争力评价 [J]. 中国环境科学, 2013,33(5):945-951.

[23]姚 峰,包安明,古丽·加帕尔,等.新疆准东煤田土壤重金属来源与污染评价 [J]. 中国环境科学, 2013,33(10):1821-1828.

[24]魏 伟,王 丽,周 平,等.安徽铜陵地区河流生态系统健康的多指标评价 [J]. 中国环境科学, 2013,33(4):691-699.

[25]Benzecri J P. Statistical analysis as a tool to make patterns emerge from data [M]. New York:Academic Press, 1969:35-74.

[26]Edet A E, Merkel B J, Offiong O E. Trace element hydrochemical assessment of the Calabar Coastal Plain Aquifer, southeastern Nigeria using statistical methods [J]. Environmental Geology,2003,44(2):137-149.

Application of support vector machine in soil environmental quality assessment.

JIANG Xue1, LU Wen-xi1*, YANG Qing-chun1, ZHAO Hai-qing2(1.Key Laboratory of Groundwater Resources and Environment, Ministry of Education,College of Environment and Resources, Jilin University, Changchun 130021, China；2.Shenyang Institute of Geology and Mineral Resources, Shenyang 110032, China). China Environmental Science, 2014,34(5)：1229～1235

This paper presented a study on the soil environment quality analysis with support vector machine method(SVM)at the Yang-cao-gou coal mine area (Jilin province, China). Incorporating field investigation and laboratory analysis, copper and lead in soil samples were measured by using inductively coupled plasma mass spectrometry(ICP-MS), the pollution characteristics of five soil heavy metals, Cd、Cr、Zn、Pb and Cu were analyzed. The nonlinear SVM classification model was employed to evaluate soil environmental quality by sigmoid kernel function programmed with MATLAB codes, and the validation process for the evaluation results was performed with fuzzy comprehensive evaluation method. Meanwhile corresponding analysis was applied to investigate the main pollution factor in each soil partition of the study area, considering the variable load size and the relationship between variables and sampling point partition. The results showed that soil environmental quality ranked almost in theⅠclass in the study area, SVM method obtained almost the same results compared with fuzzy comprehensive evaluation method with a similarity rate of 91.67%,demonstrating that the method (SVM)method is appropriate for soil environmental quality assessment. Compared with conventional assessment methods, SVM adopted the structural risk minimization principle, which resolved the problem of multi-classification, high dimensional algorithm through nonlinear to linear transfer.

support vector machine (SVM)；soil environmental quality assessment；heavy metals；Yang-cao-gou coal mine area

X825

A

1000-6923(2014)05-1229-07

2013-09-23

中国地调局项目(1212011140027,12120114027401)

* 责任作者, 教授, luwenxi@jlu.edu.cn

姜 雪(1989-),女,吉林德惠人,吉林大学博士研究生,主要从事矿山环境地质、生态水文、地下水数值模拟与优化管理等方面的研究.发表论文3篇.