预置理论圆心坐标法精密测量短圆弧零部件
2014-12-13莫贵疆谢福兵
杨 庆,李 勇,莫贵疆,谢福兵
(1.贵州红湖发动机零部件有限公司,贵州 贵阳 550018;2.贵州睿智通工程项目咨询有限公司,贵州 贵阳 550005)
引言
航空发动机、燃气轮机燃烧室不少零部件是圆形状,当中许多是由组块组合成的一个整体,其中的每一小块的圆弧面就形成一个大半径短圆弧。在加工过程中,这些圆弧面多数是加工基准面,工装上的定位基准是否准确将直接影响到产品的加工质量,因此需要对短圆弧进行测量,检验短圆弧的中心位置和半径R值,保障机加工精度。这里所说的短圆弧,是指小于30°圆心角所对的圆弧。传统的短圆弧测量方法常用光隙法(极限量规法)和弓高弦长法两种方法进行测量,但是这两种方法存在如下弊端:光隙法(极限量规法)是通过肉眼观察零件与样板的间隙,导致误差较大,对于精密圆弧的测量明显不适用;弓高弦长法是用过测量圆弧的弓高和弦长计算出圆弧的直径,然而当弓高较弦长过小或过大时,采样范围受到限制,弓高的测量误差将越大,最终导致精密圆弧的测量值误差也越大。同时当给定的理论参数与实际偏离较大时,测量效果就显著下降,此时测量结果的置信度也随之下降。实际上,短圆弧精密测量技术是一个国际公认的技术难题,弧长越短,测量的重复性也就越差[1]。在参考国内相关大半径短圆弧精密测量方法的同时,结合实践经验,总结出预置理论圆心坐标法用于测量大半径短圆弧半径R值,现对这种三坐标精密测量方法进行介绍。
1 方法与步骤
1.1 预先确定理论圆心
根据图样技术要求和零件实际情况,通过其他较高基准预先检测出待测短圆弧零件的圆弧理论圆心坐标(x′,y′),如图1所示。
1.2 选取采样点
在圆弧上选取2~20 个采样点(采样点数量根据圆弧实际形状确定),并分别将各采样点连接至圆弧理论圆心,得到多个半径值R。
1.3 求出圆弧实际半径值
将各采样点测得的多个半径值计算平均值,其结果即为圆弧的实际半径值R实,如图2所示。
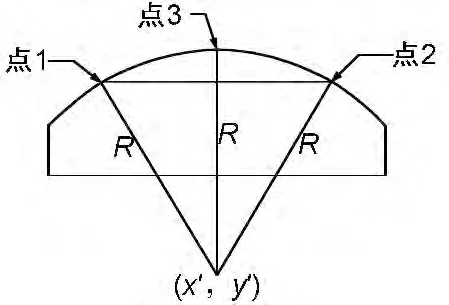
图1 圆弧理论圆心坐标

图2 圆弧实际半径值
1.4 绘制圆弧
根据圆弧实际半径值和圆弧理论圆心绘制出实际测量圆弧图形,根据短圆弧零件的设计图样尺寸公差要求,绘制出一个理论最大半径值圆弧图形(R最大)和一个理论最小半径值圆弧图形(R最小)。
1.5 对比
将绘制出的实际测量圆弧图形与一个理论最大半径值圆弧图形(R最大)和一个理论最小半径值圆弧图形(R最小)进行重叠,如果实际测量圆弧图形在两个理论极限圆弧图形范围内,则所测量的短圆弧零件是合格的。
需要指出的是,预置理论圆心坐标法对加工精度越高的零件测量效果越好,当给定的理论参数与实际偏离较大时,测量效果就显著下降,此时测量结果的置信度必须根据图样给定公差的大小而定。反之,就要对已测量的数据进行再处理,其方法是在图样给定公差范围内适当调整理论圆弧中心位置,看其原测量R值的变化,若两者均在公差范围内就视为合格。
在实践应用过程中,也会经常遇到只有一小段圆弧、无法预先给定圆心坐标或半径值的情况,此时可采用弦长中垂线法确定短圆弧圆心坐标和半径,这是根据“圆的弦的垂直平分线必然过圆心,那么无数条弦的中垂线交点必然就是圆心。”这一理论依据,大致步骤如下:
1)在待测短圆弧零件的圆弧截面上选取3~20个采样点(采样点数量根据圆弧实际形状确定),如图3 所示。
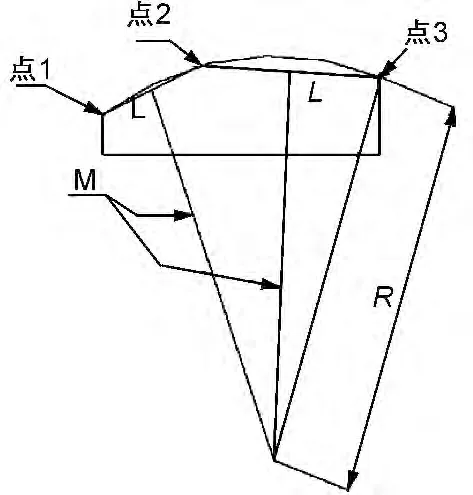
图3 弦长中垂线方法
2)将采样点两两连接,得到多个弦长段L,在每一条弦长段上绘制出其中垂线,得到多条中垂线M。
3)确定每两条中垂线的交点,并通过高斯特征组得到多条中垂线的平均数,该平均数即为圆弧的圆心坐标,采样点至圆心的距离即为圆弧的实际半径值R实。
通过以上几个步骤即可测量出圆心坐标和圆弧的实际半径值R实,然后绘制圆弧进行对比即可。在应用弦长中垂线法过程中,如果在短圆弧上取的采样点越多,这样能得到越多中垂线的交点,测量准确度就越接近真实值。
2 应用与分析
为验证该方法的可行性,通过生产的样板6060-0007和自制的工装B2Φ60 842~1 486,采用预置理论圆心坐标法进行测量应用。
2.1 样板6060-0007测量(见表1)

表1 样板6060-0007的数据分析及处理 mm
通过样板6060-0007 的误差分析,R=195.03mm 为理论最大半径值圆弧图形,R=194.97mm 为理论最小半径值圆弧图形(如图4所示),样板6060-0007的半径为R=(195.016±0.004)mm,符合图纸设计要求。
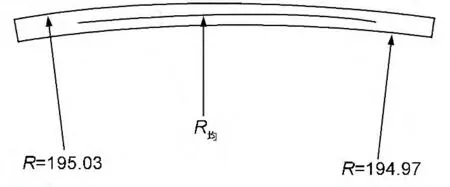
图4 样板6060-0007圆弧图形(mm)
2.2 工装B2Φ60 842-1 486测量(见8页表2)
通过B2Φ60 842~1 486 的误差分析,R=294.600mm 为理论最大半径值圆弧图形,R=294.500mm 为理论最小半径值圆弧图形(如8页图5所示),工装B2Φ60 842~1 486的半径为R=(294.024±0.014 8)mm,符合图纸设计要求。

表2 工装B2Φ60 842~1 486数据分析及处理 mm
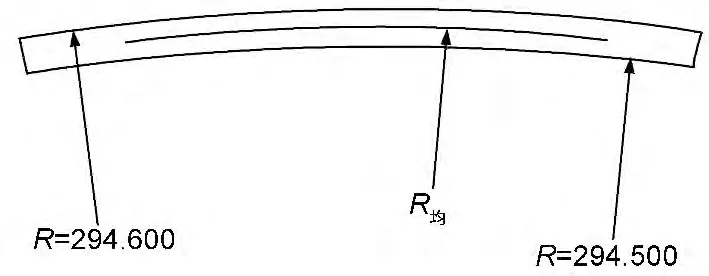
图5 工装B2Φ60 842~1 486圆弧图形(mm)
3 结语
从实践应用来看,本方法测量误差较小,提高了大半径短圆弧零件测定值的准确性和置信度,解决了传统测量技术中对大半径短圆弧零件的精密测量难题。目前该方法已推广到航空发动机、燃气轮机零部件复杂异型曲面的精确测量上,取得了良好的经济效益和社会效益。
[1]王文书.三坐标测量机对大半径短圆弧的测量实践[J].上海计量测试,2010(4):44.
