将数学建模的思想融入到经济数学中的几个典型案例

李辉

(南京财经大学应用数学学院,江苏南京 210046)

将数学建模的思想融入到经济数学中的几个典型案例

李辉

(南京财经大学应用数学学院,江苏南京 210046)

在经济数学教学中怎样将数学与经济学联系起来,培养财经类学生学习数学的兴趣是每一位从事经济数学教学的教师都应该关注的问题。本文我们介绍了将数学建模的思想融入到经济数学教学中的几个典型案例,通过这些案例教学可以将数学与经济学有机地联系起来,让数学变得既生动又符合实际,取得了很好的教学效果。

经济数学 数学建模 典型案例 教学理念

随着现代经济学的发展，经济学与数学的关系越来越密切，数学语言已成为表达经济学思想的标准的分析工具，许多经济学模型本质上就是数学模型，同时经济学中的某些问题也是数学的新的生长点。基于此几乎所有的财经类高校都将数学列为重要的基础课进行开设，这门课程称作为经济数学，如果要给经济数学下个定义的话，可以这样来描述：“经济数学，即在经济中应用的数学，它是经济学与数学相互交叉的新的跨学科领域。”在财经类高校怎样将经济学与数学有机地联系起来，培养学生学习数学的兴趣，是每位从事经济数学教学的教师都应该思考的问题。根据我们教学团队多年的教学实践和探索，我们在教学中始贯穿这样的教学思想来讲授经济数学课程，即从经济问题入手，讲清楚经济问题与数学之间的联系，通过数学建模将经济问题转化为数学问题，再用数学方法加以解决，让数学揭开经济问题的奥秘。看来将经济问题与数学联系起来的关键是数学建模。下面我们介绍将数学建模的思想融入到经济数学教学中的几个典型案例。

1 案例一:降价能增收吗

在市场竞争中，商品价格大战随处可见。例如，手机价格大战，电视价格大战，空调价格大战，……。那么，降价能增收吗？下面通过数学建模及微积分的方法来揭开其中的神秘面纱。假设商品的需求量Q只与商品的价格p有关，即需求量Q是商品的价格p的函数Q=f(p)。设价格p的改变量为△p，价格改变的百分比为△p/p，需求量Q的改变量为△Q，需求量改变的百分比为△Q/Q。现在我们要问：当价格改变1%时，需求量改变百分之多少？我们可以用量(△Q/Q)/(△p/p)来描述。

设收益为R，则R=pQ，于是

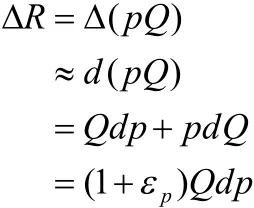
我们得到收益与价格之间关系的数学模型

根据上面的讨论，我们通过数学建模及微分学的知识完全解读上面提出的问题。

2 案例二:怎样度量收入分配的不平等程度

随着市场经济的发展，许多国有企业都进行了股份制改造，一大批股份制企业的老总都成了名副其实的富翁。但我们也应该看到，近年来，我国的贫富差距确有不断扩大的趋势，如何反映这种贫富差距的状况呢？下面通过数学建模和积分学的知识来分析这个问题(如图1)。

在上载的时候，视频资料的音频质量要求是以监听声音为主，辅以上载模块提供的软件示波器，以UV表进行监控。特别需要注意：(1)资料内容出现差错，或者应该是整体但内容有缺失不完整；(2)技术人员通过主观判断图像或声音质量较差的；(3)出现夹帧或彩条、黑场、静止等不规范画面，持续时间较长，超过5 s的；(4)出现滚动、跳闪、波纹或花屏、杂波大、马赛克严重等特别明显信号的；(5)音量大小不均或者偏大偏小，失真不清晰，有杂音噪声干扰，明显中断等。在资料上载过程中，针对出现的质量问题要及时反馈给相关人员进行补救；如无法处理的，要注意看是否有必要上载该素材，或者在上载的资料中进行说明。

横轴OH表示人口(按收入由低到高分组)的累计百分比，纵轴OM表示收入的累计百分比。当收入完全平等时，人口累计百分比等于收入累计百分比，用直线OL表示，当收入完全不平等时，用折线OHL表示。实际上，一般国家的收入分配，既不会是完全平等，也不会是完全不平等，而是在两者之间，即曲线ODL。很显然，曲线ODL与直线OL的偏离程度的大小，决定了该国国民收入分配不平等的程度。以横轴OH为x轴，纵轴OM为y轴，y=f(x)表示曲线ODL，则不平等面积：

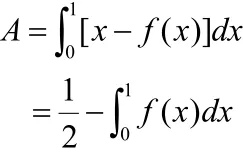
不平等面积A所占最大不平等面积(A+B)的比例

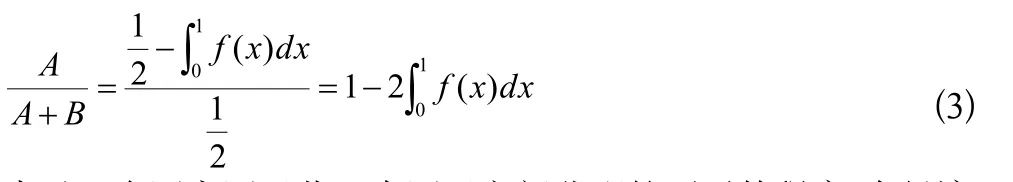
表示一个国家国民收入在国民之间分配的不平等程度，在经济学上称为基尼系数，记作G。

通过上面的分析，我们可以看到用定积分模型就可以度量一个国家国民收入分配的不平等程度，这是多么有意义的一件事情啊！

3 案例三:在产业集群中模块化程度越高价值就越大吗

随着信息技术的发展，模块化对于当今世界范围内的产业结构调整和升级起着至关重要的推动作用，当今的产业已经进入到模块化设计、生产、消费的大发展时期。模块化的概念最早由哈佛商学院的两位院长CarlissY.Baldwin和KimB.Clark于1997年在《哈佛商业评论》的文章中提出，两位作者在该论文中指出，模块化现象在几个产业领域里从生产过程扩展到了设计过程，并且敏锐地指出了模块化对产业结构调整所具有的革命性意义。模块是指半自律性的子系统，通过和其他同样的子系统按照一定的规则相互联系而构成的更加复杂的系统或过程。根据这个概念，将一个复杂的系统或过程按照一定的联系规则分解为可进行独立设计的子系统的行为，我们称之为模块化分解。按照某种联系规则将可进行独立设计的子系统统一起来，构成更加复杂的系统或过程的行为，我们称之为模块化

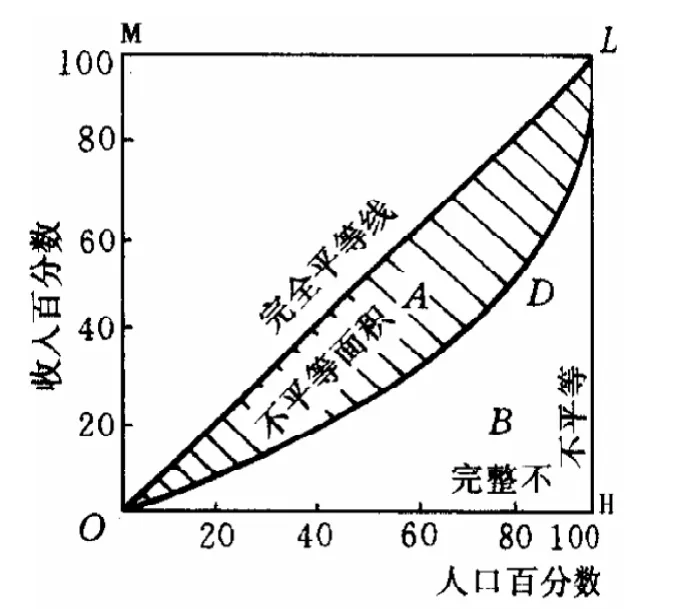
图1

在产业集群中模块化程度越高价值就越大吗？下面我们用数学建模和概率论的知识来解答该问题。为了定量讨论模块化的价值，我们先作几个假设：

(1)假设整体系统是由n个有价值的模块组成的，这n个模块的价值相加就是整体系统的价值。

(2)设整体系统含有N个设计参数，第j个模块所含有的设计参数为

(3)随着技术进步，模块化成本不断降低。相对于模块化创造的价值而言，模块化成本可以忽略。设整体系统的价值为X，它是一个随机变量，它是由大量相互独立的随机因素(设计指标)的综合影响所形成的，而其中每一个别因素在总的影响中所起的作用都是微小的，根据概率论中的中心极限定理，我们认为X服从均值为0，方差为的正态分布，即

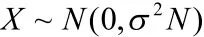
假设第j个模块设计结果的价值为Xj，它也是一个随机变量，假设Xj服从均值为0，方差为的正态分布，即相互独立，于是模块化后整个系统的价值为：

其中S0为整个系统模块化前所具有的价值，称为基准价值；

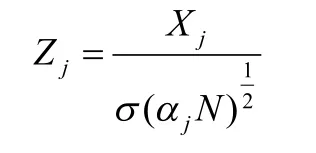
则Zj服从标准正态分布，即

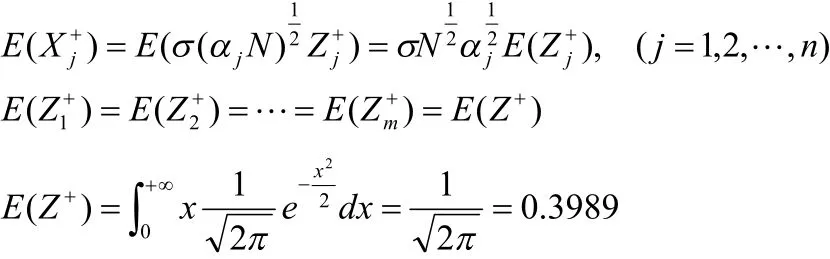
这样(1)式就变为：

于是得到下面的结论：

在上面模型的假设下，具有N个设计参数的整体系统被分成n个分别具有设计参数的的模块，模块化所带来的价值为：

因为

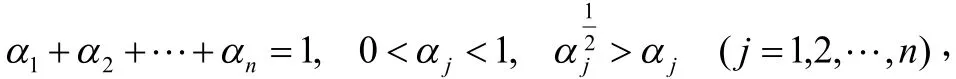
所以

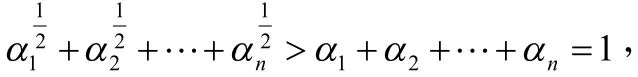
由(8)式知：

由此可得到关于模块化价值的下面的结论：

4 结语

采用模块化比不采用模块化将获得更大的价值。且随着技术进步带来分工的进一步深化，模块化程度越高(模块数越多)，价值也越大。以上是我们将数学建模的思想融入到经济数学教学中的几个典型案例，通过这些案例教学，可以将数学与经济学有机地联系起来，让数学变得既生动又贴近实际，也提高了财经类学生学习数学的积极性。今后我们会将这种教学理念始终贯穿在整个经济数学教学的实践中，并在教学实践中不断完善，为财经类院校培养出具有创新能力的有用人才。

[1]张从军,王育全,李辉,刘玉华.微积分(第二版)[M].上海:复旦大学出版社,2009.

[2]黎诣远.经济数学基础[M].北京:高等教育出版社,1998.

[3]钱书法,李辉.企业共生模式演进及其原因分析[J].经济管理,2006,398(14):47-53.

[4]Baldwin,Carliss Y．and Kim B．Clark.Managing in an Age of Modularity[J].Harvard Business Review,1997,75(5):84～93.

[5]史树中.诺贝尔经济学奖与数学[M].北京:清华大学出版社,2002.

南京财经大学教改项目(JGZ1304)。集成。模块化结构主要由三个部分构成。(1)“设计规则”。设计规则由在行业内具有核心竞争力，有品牌产品且占主导地位的企业来制定；(2)“模块”。按设计规则将整个系统分解成若干个子系统，称其为模块，每个模块必须遵守设计规则，但其具体操作可以独立进行；(3)“系统集成与检验模块”。对模块进行检验，选择符合规则的模块并组装成系统，并使各模块间在整个系统中达到和谐。