采用土壤孔隙表面分形维数预测土壤水分特征曲线

刘亚磊，梁 杏，2，朱常坤，李 静

(1.中国地质大学(武汉)环境学院，湖北武汉 430074;2.中国地质大学(武汉)生物地质与环境地质国家重点实验室，湖北武汉 430074)

分形理论是由 Mandelbrot［1］提出，用来研究无规则图形以及复杂结构特征的方法。分形是度量上述土壤物理因素的一种手段，分形维数则是其具体的表现形式［2］。Bartoli［3］和 Tyler等人［4］发现:反映土壤质地和结构的物理因素，如容重、粒径分布、孔隙度及孔隙的连通状况等，都表现出分形特征，这些物理因素对土壤的水力参数存在直接或者间接的影响。因此，国内外学者［4～7］开展了利用土壤相关物理因素的分形维数研究土壤水力参数的工作，并在前人的基础上不断提出新的看法与改进手段:Tyler等［4］首先将分形理论成功地应用于预测土壤水分特征曲线，提出了相应分形模型并将其扩展到三维空间。Kravchenko［8］对Tyler-Wheatcraft模型进行改进，提出了一种根据土壤颗粒分析数据分段计算孔隙表面分形维数的方法，并分段估计土壤水分特征曲线，取得了较好的结果;Toledo等［9］利用分形方法建立水力传导率模型;在上述基础上，刘建立等［10］由土壤颗粒质量分布曲线计算得出孔隙表面分形维数，并利用Burdine模型和Mualem模型预测非饱和水力传导度，预测精度较高。分形理论的引入使得间接计算土壤水力参数多了一种简便而且准确的方法。

但是，王国梁等［11］认为由不同粒径的土壤颗粒质量计算分形维数存在不合理的假设，提出由土壤颗粒体积的大小和数量来计算体积分形维数;杨金玲等［12］采用激光衍射法与吸管法实测了土壤的粒径分布，计算并比较颗粒的质量分形维数和体积分形维数，发现二者间存在一定的线性相关关系。随着科技的进步，激光衍射可以快速获取土壤颗粒体积累积曲线，独立于颗粒质量法，可以得到土壤任意两粒径之间的体积百分含量。利用颗粒体积分布曲线计算的孔隙表面分形维数，可以避免斯托克斯公式中不合理的假设，探讨此法预测土壤水分特征曲线在国内相关研究中并未见报道。

本文采用土壤颗粒体积分布计算土壤孔隙表面分形维数，结合de Gennes分形模型，预测土壤水分特征曲线，通过与实测数据的对比分析，探讨采用土壤颗粒体积分布曲线计算表面分形维数预测土壤水分特征曲线的合理性。

1 确定表面分形维数的原理

土壤的孔隙大小分布状况对土壤的水分特征曲线有重要影响，而孔隙表面分形维数则是描述三维空间内土壤孔隙表面不规则性的一种量度。为了确定此分维，刘建立［10］等基于 Kravchenko 和 Zhang［8］提出的一种由土壤粒径分布曲线计算孔隙表面分形维数的方法，在孔隙体积与孔隙半径的对应关系下，建立了土壤颗粒质量累积曲线与孔隙表面分形维数之间的函数关系。本文参考刘建立［10］等的推导过程进行公式推演，具体步骤如下:

Pachepsky［13］认为孔隙体积增量 dVp(≤r)和 dVp(＞r)与孔隙半径r之间存在如下关系:

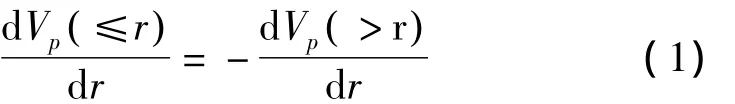
而Perrier［14］等根据孔隙体积与孔隙半径之间的关系提出孔隙体积增量的一种变化形式:

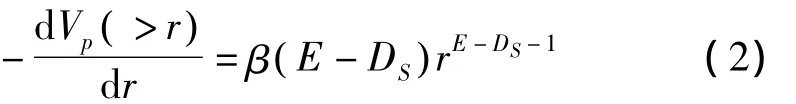
式中:E——欧氏几何中的拓扑维数，E=3;

β——常数;

DS——孔隙表面分形维数。

假设土壤孔隙为圆柱状，土壤孔隙体积可表示为:

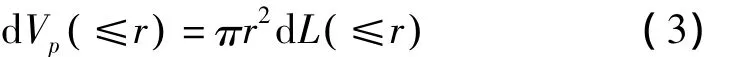
此处认为土壤孔隙最小半径为0，结合式(2)、(3)可求出孔隙半径小于等于r的孔隙长度L(≤r)为:

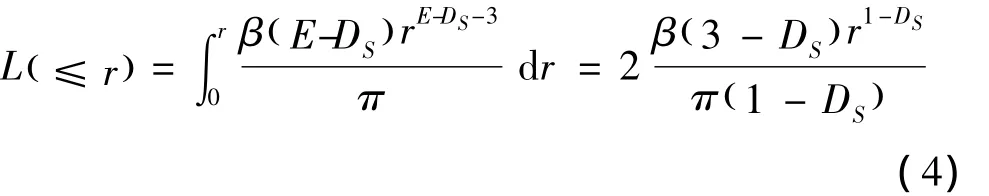
Tyler等［5］认为N个等价半径为R的固体颗粒构成的毛细管长度为l(R):

式中:R——颗粒粒径;

N——颗粒粒径为R时的颗粒数量;

D——弯曲毛细管的孔隙分形维数，Kravchenko等［8］认为 D=DS-1。

Kravchenko等［8］假设土粒密度 ρs不变，认为个数N可以由半径为R的颗粒的质量W(R)计算出来，即:

本文采用土壤颗粒体积V(R)计算相应粒径级别下的颗粒数量，避免了上式中关于土粒密度不变的假设，得到个数N的计算式:

式中:S——土壤颗粒形状的系数;

e——孔隙比，即孔隙体积与颗粒体积之比:

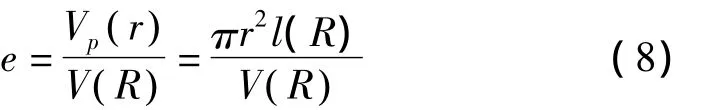
r是颗粒半径为R时组成的土壤孔隙半径。假设R最小为0，对式(5)进行积分可得由半径小于等于R的颗粒组成的孔隙半径小于等于r的孔隙累计长度:

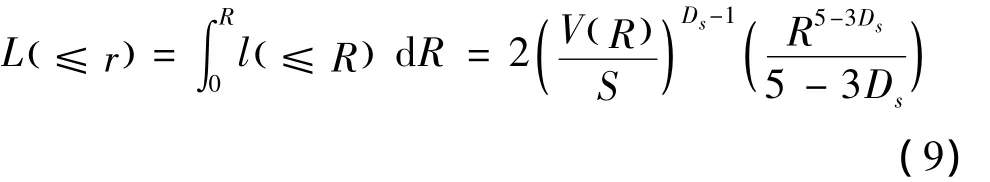
综合式(4)、(8)和(9)，可得半径为R的颗粒累积V(R)关于土壤孔隙表面分形维数之间的关系式:

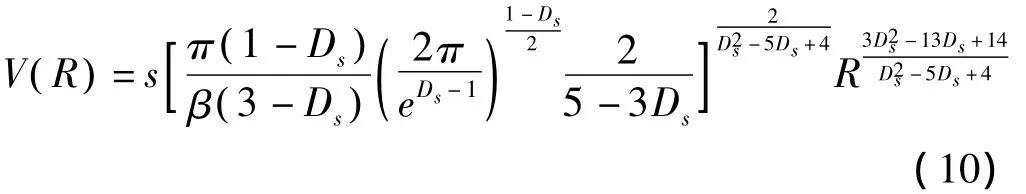
对上式进行积分则可得半径小于等于R的土壤颗粒的累积体积，假设最小半径为0:

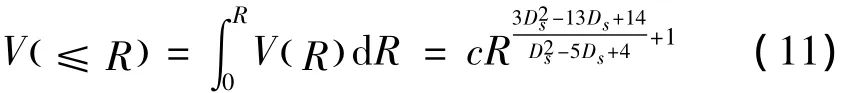
式中:c——常数项。

对式(11)两边取对数得:

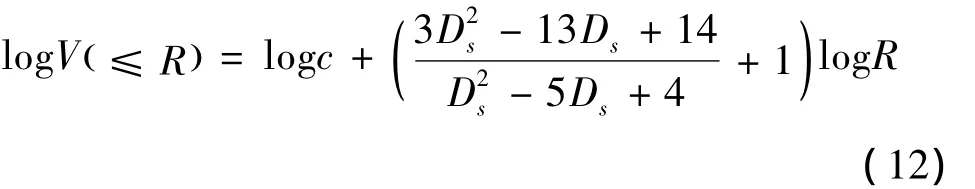
式(12)与Kravchenko和刘建立等人建立的方程是相似的，只是将土壤累积质量W(≤R)替换为累积体积V(≤R)，此式的优点是不必假设各级土壤颗粒密度不变，累积体积则可由激光衍射法测试得出。本文中所用颗粒半径为相应粒径分级的上限值与下限值的算术平均值，通过上式与土壤颗粒体积的累积曲线，可计算土壤的表面分形维数Ds。

2 土壤水分特征曲线的分形模型

利用土壤的分形维数预测土壤水分特征曲线，众多学者按照不同的理论提出多种预测模型。

de Gennes［16］根据土壤孔隙表面是由自相似性的孔洞互相嵌套组成或者团聚体连接而成的两种模式下分别导出的预测模型如下:

式中:Ψ——负压绝对值;

Ψa——进气值;

θs——饱和含水量。

Perrier等［14］根据孔隙体积增量的变化形式，即式(2)，提出一种水分特征曲线的分形模型:

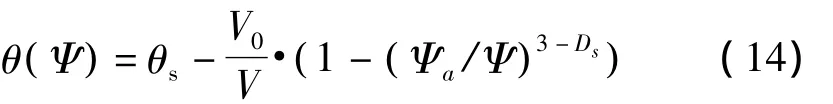
式中:V0——孔隙半径为0时的孔隙体积;

V——总体积。

刘建立等［10］人假设 V0/V=θs- θr(θr为残余含水量)，代入式(14)即与Brooks-Corey模型一样:

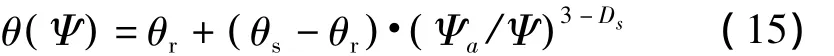
由于 θr对上式的影响不敏感，θr≈0，代入式(15)，其形式与式(13)完全相同。因此，选取式(13)作为本文预测土壤水分特征曲线的分形模型，采用Brooks-Corey模型作为拟合实测曲线的参考模型。

3 应用实例

3．1 土壤样品与粒径分级

本文中所用到的材料为华北平原辛集地区土样(表1)。

采用张力计法进行土壤水分特征曲线的实测;通过激光粒度仪对测试土样进行颗粒分析，获取土壤颗粒体积累积曲线。

本文所用样品主要为细粒土，土壤颗粒最大半径小于 1mm(表 1)。结合 Kravchenko［8］与郭中领［16］等人的研究成果，基于美国土壤质地分类系统，进行以下几种粒径分级(表2)。对不同的分级方法分别进行表面分形维数的计算。

3．2 表面分形维数计算

由所获取的颗粒体积累积曲线，分别按照表2所列的四种不同分级方法，以lg(Rave)、lg［V(≤R)］为X、Y轴(图1)，基于最小二乘法的线性回归，得出二者关系曲线的斜率K。

表1 土壤样品颗粒分级情况Table 1 Particle-size class of samples

表2 不同粒径分级方法Table 2 Different methods for grading particle-size class

结合式(12)有K与Ds的关系:

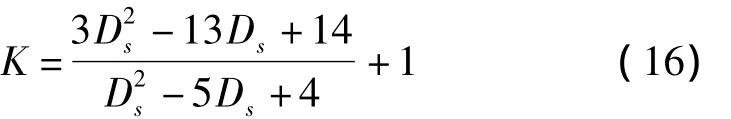
对式(16)进行求解，由于为三维空间，取两个计算结果中较大的数值为DS，结果见表3。

由表3可以发现，Ds处于2.37～2.91之间。不同分级方法中，颗粒分级界限的最大半径越小，累积体积对数与粒径半径对数之间的相关系数越大，即:D1＞D2＞传统7级，说明利用颗粒体积分布计算表面分形维数同样存在无标度区间。计算结果显示随着样品粘粒含量的减少，质地越粗，表面分形维数逐渐降低的规律，与其他学者计算的分形维数规律是一致的。四种分级计算结果相比较，D3计算得到的表面分形维数处于D2与传统7级之间，且与D2计算的结果间差距较小，说明增大分级密度对计算表面分形维数影响不大;采用不同粒径分级方法计算会影响表面分形维数的大小，但不影响其反映的物理意义。

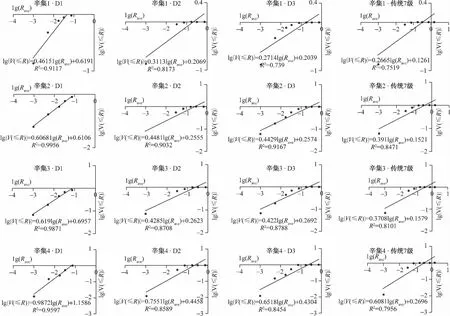
图1 不同分级方法下K的拟合图(部分)Fig．1 Slope coefficients of different particle-size grading methods

表3 计算得DS值与相关系数Table 3 DSand related coefficient of samples

3．3 实验法获取SWRC

本节选取辛集1～4号样品进行土壤水分特征曲线的参数拟合与预测分析。首先将1～4号原状样通过张力计与称重方式获取试样的土壤水分特征曲线，通过RETC软件中的Brooks-Corey模型进行拟合求参，获取进气值Ψa，并与预测拟合结果对比。表4为所选4个样品的参数拟合结果。

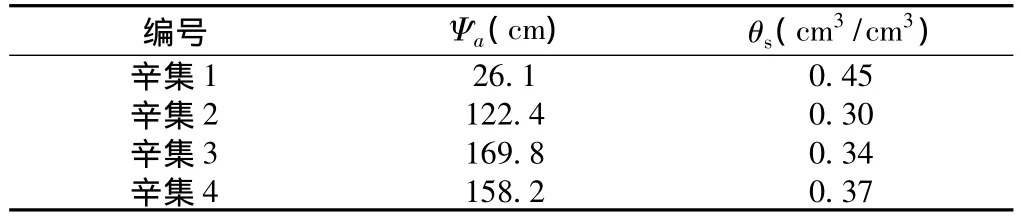
表4 土壤水分特征曲线拟合参数Table 4 The fitted parameters of SWRC

3．4 利用分形维数进行SWRC的预测

分别将D1和D2两种分级计算的表面分形维数(表3)与表4中所列参数代入de Gennes预测模型(式14)，绘制预测土壤水分特征曲线(图2);并采用均方根误差RMSE作为衡量预测模型与实测值之间准确性的计算标准(以含水量作为评价值)，见式(17):

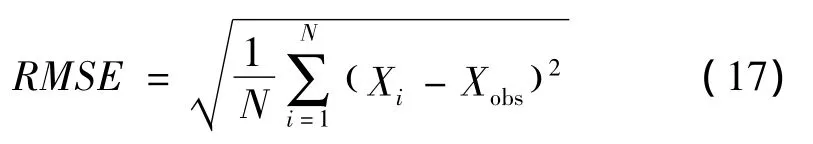
式中:Xobs——实测值;

Xi——预测值，i=1，2，3，…，N。

由图2可以很直观地发现，采用D1分级方法计算出的表面分形维数预测的土壤水分特征曲线与实测值拟合得好，而通过D2进行的计算结果相对较差(表5)。

图2 两种分形维数下土壤水分特征曲线的预测值与实测值Fig．2 Prediction and observed points of SWRC by using two kinds of surface fractal dimension

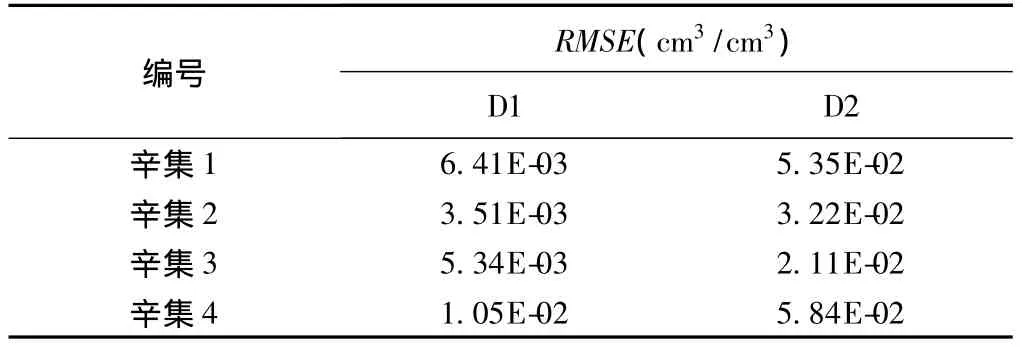
表5 预测与实测的RMSE值Table 5 The RMSE of prediction and observed points

对D1分级方法的预测结果进行分析:最大的均方根误差出现在4号土样，为0.0105cm3/cm3，而其他三个土样的RMSE均小于0.01cm3/cm3，也就是说，采用此种分级方法计算得出的表面分形维数对预测土壤水分特征曲线具有较高的适用性，尽管3号土样在高吸力段的预测值与实测值略有偏差，但其他试样的预测结果在整个吸力范围内与实测值较匹配。D2的预测结果与实测值只有在低吸力段匹配较好，随着吸力的增加，预测值与实测值出现较大偏差，土样预测值与实测值之间的RMSE≥2.11E-02cm3/cm3。

4 结论

(1)利用土壤颗粒体积累积曲线计算表面分形维数，避免了土壤颗粒密度不变的假设，改善了计算过程中的缺陷。

(2)相同试样由不同颗粒分级方法计算得出的表面分形维数大小不同;相同分级方法下，试样的表面分形维数随着土壤粘粒的减少而变小，符合一般规律;即颗粒分级方法的不同不影响其反映的物理意义。

(3)按照D1计算的表面分形维数预测土样吸力大于进气值的曲线趋势精度高，误差小，这是由于土壤负压超过进气值后，土壤水分特征曲线主要受由半径小的颗粒组成的细小孔隙控制，从侧面说明土壤孔隙对水力参数的影响。因此，此法可以用于预测更高吸力值情况下的曲线变化趋势;而D2的情况，其预测的效果较差，误差偏大，但可以满足田间粗略估计的需要;应用土壤颗粒体积累积曲线在无标度区间内计算的表面分形维数更适合以de Gennes模型来预测细粒土的土壤水分特征曲线。

(4)笔者认为，利用颗粒体积累积曲线计算表面分形维数的方法比较适用于相对均质的土样，可以避免由于参与颗粒分析的样品量少而不具有代表性的不利影响。在无标度区间计算的表面分形维数预测结果较好，这可能是由于大于0.1mm的土壤颗粒组成的孔隙并不具有很强的自相似性从而影响分形维数的计算。因此，利用土壤颗粒体积累积曲线按照无标度区间计算表面分形维数，从而预测土壤水分特征曲线是可行的，此法具有较明确的物理意义。

［1］ Mandelbrot B B.The fractal geometry of nature［M］.San Francisco:W H Freeman，1983.

［2］ 任权，王家鼎，袁中夏，等.高速铁路地基黄土微结构的分形研究［J］.水文地质工程地质，2007，34(6):76-82.［Ren Q，Wang J D，Yuan Z X，et al.Fractal study on loess microstructure of one high-speed railway foundation［J］.Hydrogeology ＆ Engineering Geology，2007，34(6):76-82.(in Chinese)］

［3］ Bartoli F.Structure and self-similarity in silty and sandy:the fractal approach［J］.Soil Sci，1991，42:167-185.

［4］ Tyler S W，Wheatcraft S W.Fractal scaling of soil particle-size distribution:Analysisand limitations［J］.Soil Sci.Soc.Am.1992，56:362-369.

［5］ Tyler S W，Wheatcraft S W.Application of fractal mathematics to soil water retention estimation［J］.Soil Sci Soc Am，1989，53:987-99.

［6］ 杨培岭，罗远培，石元春.用粒径的重量分布表征的土壤分形特征［J］.科学通报，1993，38(20):1896-1899.［YANG P L，LUO Y P，SHI Y C.Fractal feature ofsoilon expression by weight distribution of particle size［J］.Chinese Science Bulletin，1993， 38(20):1896-1899.(in Chinese)］

［7］ 杨建，陈家军，杨周喜，等.松散砂粒孔隙结构、孔隙分形特征及渗透率研究［J］.水文地质工程地质，2008，35(3):93-98.［YANG J，CHEN J J，YANG Z X，et al.A study of pore structure，pore fractal feature and permeability of unconsolidated sand［J］.Hydrogeology＆ Engineering geology，2008，35(3):93-98.(in Chinese)］

［8］ Kravchenko A，Zhang R D.Estimating the soil water retention from particle 2 size distributions:A fractal approach［J］.Soil Science，1998，163:171-179.

［9］ Toledo P G，Novy R A，Davis H T，et al.Hydraulic conductivity of porous media at low water content［J］.Soil Science Society of America Journal，1990，54:673-679.

［10］ 刘建立，徐绍辉，刘慧，等.确定田间土壤水力传导率的分形方法［J］.水科学进展，2003，14(4):464-469.［LIU J L，XU S H，LIU H，et al.Fractal method for estimating field hydraulic conductivity function from soilparticle-size distribution［J］.Advances In Water Science，2003，14(4):464-469.(in Chinese)］

［11］ 王国梁，周生路，赵其国.土壤颗粒的体积分形维数及其在土地利用中的应用［J］.土壤学报，2005，42(4):545-550.［WANG G L，ZHOU S L，ZHAO Q G.Volume fractal dimension of soil particles and its applications to land use［J］.Acta Pedologica Sinica，2005，42(4):545-550.(in Chinese)］

［12］ 杨金玲，李德成，张甘霖，等.土壤颗粒粒径分布质量分形维数和体积分形维数的对比［J］.土壤学报，2008，45(3):415-419.［YANG J L，LI D C，ZHANG G L，et al.Comparison of mass and volume fractal dimensions of soil particle-size distributions［J］.Acta Pedologica Sinica，2008，45(3):415-419.(in Chinese)］

［13］ Pachepsky Y A，Shcherbakov R A，Korsunskaya L P.Scaling of soil water retention using a fractal model［J］.Soil Science，1995，159:99-104.

［14］ Perrier E，Rieu M，Sposito G，et al.Models of water retention curve for soils with a fractal pore size distribution［J］.Water Resources Research，1996，32:3025-3031.

［15］ de Gennes P G.Partial filling of a fractal structure by a wetting fluid［C］//Adler D.Physics of Disordered Materials.New York:Plenum Press，1985:227-241.

［16］ 郭中领，符素华，张学会，等.土壤粒径重量分布分形特征的无标度区间［J］.土壤通报，2010，41(3):537-541.［GUO Z L，FU S H，ZHANG X H，et al.Scale-ree Domain of Fractal Characteristic of the Soil Particle-size Distribution［J］.Chinese Journal of Soil Science，2010，41(3):537-541.(in Chinese)］