随机微分方程在人口预测中的应用

单传朋 淩斌斌 张伟

(安徽工程大学数理学院,安徽芜湖 241000)

随机微分方程在人口预测中的应用

单传朋 淩斌斌 张伟

(安徽工程大学数理学院,安徽芜湖 241000)

本文对中国总人口数量构建随机Logistic模型,结合历史数据估计了模型参数,利用该模型对中国总人口数量进行了预测,预测结果较好。

随机微分方程 极大似然估计 随机Logistic模型

人口问题是当前世界上人们最关心的问题之一。认识人口数量的变化规律,作出较准确的预报,是有效控制人口增长的前提之一。

假设人口增长服从Logistic模型:

1 参数估计

李群[1]在 K已知或者可以估计出的条件下,给出了 r和 β的极大似然估计(取 θ=1情形):

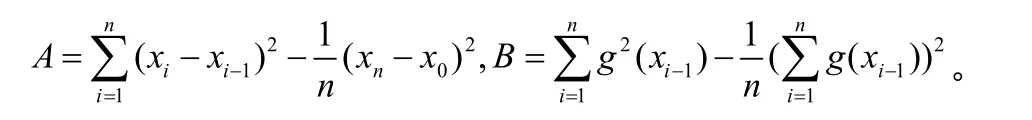
其中环境最大容量 K是常数,于是假设 K不受随机扰动的影响,利用常微分方程估算出来的 K的值可以用于随机情形。在这里直接对(2)式所对应的(1)式对 K用数据拟合。

选取1990-2013年全国人口总数(万)来估计参数,数据[2]如表1:

由赵静[3]拟合可得环境容量 K=143654.342, β=0.01021501845 98, r=0.06633254401474。

表1

表2

表3

2 模拟仿真

将所得模型离散化,时间间隔取1年,得到:

其中 dB为标准布朗运动在一个单位时间的增量。

通过编写Matlab[4]程序将参数带入模型进行计算可以计算出人口的拟合值:

从表2可以看到误差百分比(绝对值)都大概在0.2%左右,并且计算得到其平均值是0.2056%,模型拟合的效果非常好,利用此模型来对未来人口数量进行预测(如表1)。

图形中用’+’表示真实的人口数据,连线表示从1991年到2013年的拟合值,后面的’o’表示对未来10年(2014年到2023年)的预测值

(见图1)。

3 结论与展望

通过所给数据和图形的结果可以看出,由于人口会经常受到环境白噪声的干扰,随机Logistic模型的拟合效果相当好,同时也可以看出随着时间的推移和人口的增长,人口的自然增长率呈现出负指数的下降趋势,并逐渐趋近于零,人口在十年后趋近于13.9557亿左右。而加入了随机扰动之后的Logistic模型对于预测有了更好的效果,通过检验可以看出模型的拟合效果非常显著,同时可以看出人口在二十年之后会向14.1亿左右趋近并得到平衡。

[1]李群.一类随机微分方程的参数估计[M].应用数学.2012,25(4):771-776.

[2]http://www.stats.gov.cn/tjsj/.

[3]赵静等.数学建模与数学实验[M].北京:高等教育出版社,2000.

[4]Desmond J. Higham An Algorithmic Intr oduction toNumerical Simulation of Stochastic Differential Equations .SIAM REVIEW.2001,43 (3): 525-546 .

单传朋,淩斌斌,安徽工程大学数理学院统计学系102班。

安徽工程大学大学生创新训练项目 (201210363209),安徽工程大学教研项目(2010xjy32) 安徽工程大学青年基金资助项目(2005YQ006)。